這個存儲庫,我將使用Python實施一些著名的算法。該算法是根據所使用的策略排列的。每種算法將對它試圖解決的問題和一些相關資源都有解釋。
(該存儲庫的目的是為我所回顧的所有這些出色的算法創建一個美麗的讀數。)
內容:
本節,我將討論著名的鴻溝和征服策略,並展示此策略的某些應用。
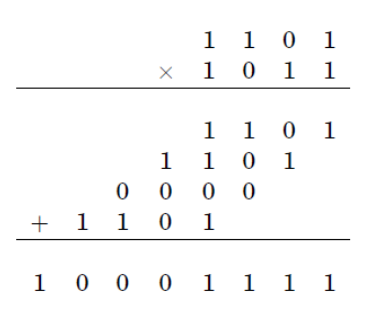
乘以兩個N數字的標準過程需要與成正比的許多基本操作。至於Karatsuba算法,它最多減少了運行時間
關鍵主意
Karatsuba算法的基本步驟是一個公式,該公式允許一個公式計算兩個大數字的乘積,並使用三個較小數字的乘法,每個數字的數字大約是或數字的一半,以及一些添加和數字偏移。
特性
Back to Top
該算法最糟糕的運行時間是。
上面的GIF顯示合併排序的工作方式: 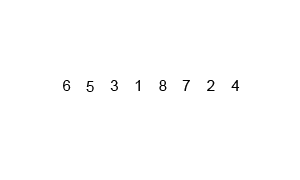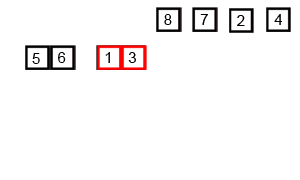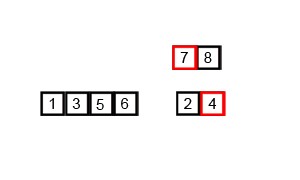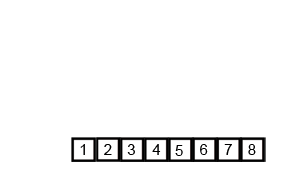
關鍵主意
將未分類的列表分為n個sublist,每個列表包含1個元素(1個元素的列表被認為是分類的),然後反複合並訂書片以產生新的排序訂閱者,直到只剩下1個sublist。這將是排序列表。
特性
Back to Top
關鍵主意
像上圖一樣,當我們在合併操作中首次從右子陣列中接收元素時,這表明右元素小於(左子陣列的長度 - 左元素的索引)元素。
隨著算法的進行,添加所有反轉將為我們提供總倒置。
特性
Back to Top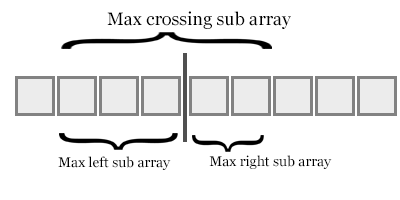
特性
Back to Top本節我將討論兩種算法,這些算法在內部使用了隨機變量。
關鍵主意
QuickSort首先將一個大陣列分為兩個較小的子陣列:相對於隨機選擇的元素,低元素和高元素。然後,QuickSort可以遞歸對子陣列進行分類。因此,快速排序的關鍵點是選擇分區元素。
特性
Back to Top
關鍵主意
通過獨立的隨機選擇重複收縮算法時間並返回最小的切割,找不到最小切割的概率是
特性
Back to Top將數據結構作為獨立部分具有誤導性;但是,我將引入令人困惑的問題,這些問題由數據結構優雅地解決。一些數據結構可能具有尚未審查的算法設計策略。
關鍵主意
BFS用於計數從無向圖或有向圖中的源節點的可觸發節點。可及的節點按找到的順序打印。隊列用於存儲節點彩色灰色(請參見下面的GIF)。 BFS中的“廣度”一詞意味著找到最短長度的可觸及節點。寬度延伸了訪問的節點和未發現的節點之間的邊界。
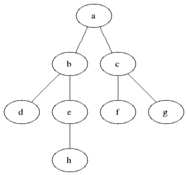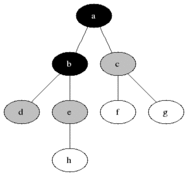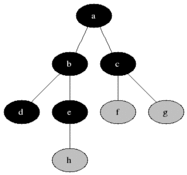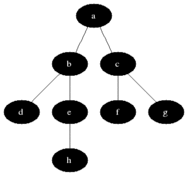
特性
Back to Top
關鍵主意
DFS在有向圖中使用,它告訴源節點可以通過我們找到的順序打印出多少節點。我們使用堆棧存儲我們將其分類為圖形的開始點的節點。其名稱的“深度”意味著該算法將盡可能深入地進行,當它到達端點時,它將返回到啟動節點。
特性
Back to Top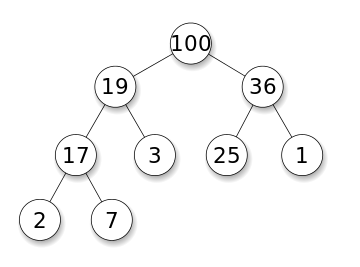
中間維護問題是,如果從數據流中讀取整數,請找到有效的元素中位數。為簡單起見,假設沒有重複。
關鍵主意
我們可以在左側使用最大堆來表示中位數不足的元素,右側的最小堆代表了比有效中值大的元素。當兩個堆的大小之間的差異更大或等於2時,我們將一個元素切換到另一個較小的尺寸堆。
特性
Back to Top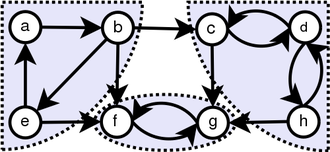
關鍵主意
通過簡單的觀察,我們發現圖的tranpose具有與原始圖相同的SCC。我們兩次運行DFS。第一次,我們在G上運行它,並為每個頂點計算完成時間。然後,我們在g^t上運行DFS,但是在DF的主環中,以減少完成時間的順序考慮頂點。
特性
Back to Top
關鍵主意
在無向圖中,我們可以使用此數據結構來找出多少SCC。下圖顯示了其工作原理。
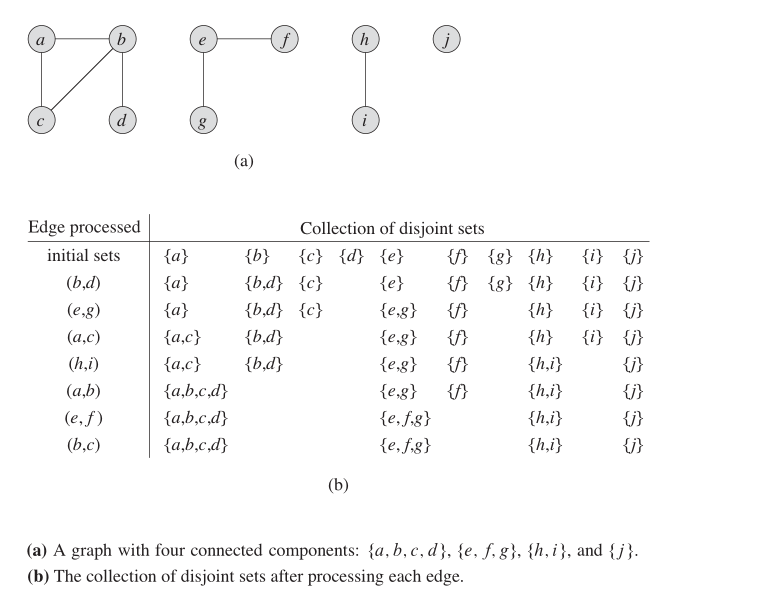
特性
Back to Top在本節中,我將介紹一種強大的算法設計策略,這是一種貪婪的算法。
從維基百科(Wikipedia),一種貪婪的算法是一種算法範式,遵循解決問題的啟發式方法,即在每個階段[1]進行本地最佳選擇[1],希望能找到全球最佳選擇。在許多問題中,貪婪的策略通常不會產生最佳解決方案,但是貪婪的啟發式方法可能會產生本地最佳解決方案,在合理時間內近似全球最佳解決方案。
在活動選擇問題中,每個活動都有其自身的體重和長度。我們的目標是最大程度地減少重量*的總和。這是一個非常簡單且很好的例子,可以顯示貪婪算法的工作原理,並使用參數交換技術提供優雅的證明。
關鍵主意
如果我們按價值/長度進行分類,我們可以證明現有的最佳結構不能比這種安排更好。 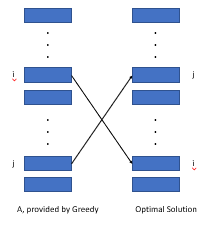
如上圖所示,我們考慮了兩種活動在兩個安排中範圍有所不同的成本(i,j)。我們發現,通過Wi*lj -wj*li的值,貪婪算法中的成本小於最佳結構,該值大於或等於0。
特性
Back to Top
關鍵主意
我們根據陣列的完成時間對數組進行了排序。該算法提出了第一份工作時間比上一個工作時間更大的工作。
特性
Back to Top
編碼本書的一種方法是使用固定長度編碼。如下所示:
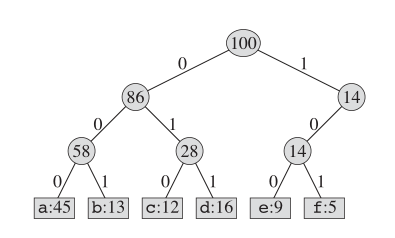
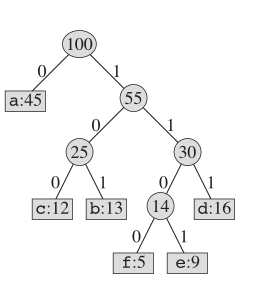
至於霍夫曼編碼,實際的樹結構看起來像這樣:
關鍵主意
我們維護二進制樹,並創建一個新節點作為兩個最小頻繁的字母的父。這個新節點的關鍵是其兩個孩子的鑰匙之和。我們重複此操作,直到這本“書”中沒有節點。
特性
Back to TopDijkstra的算法是用於查找圖中節點之間最短路徑的算法。但是,它具有一個先決條件,所有路徑必須更大或等於0。
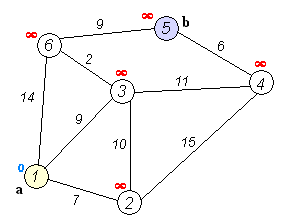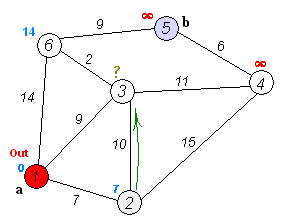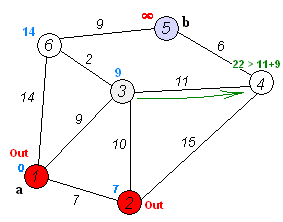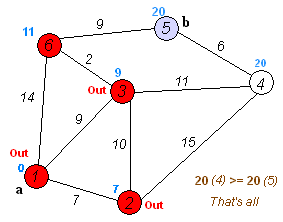
關鍵主意
單獨的節點分為兩組,一組被標記為探索。然後,我們更新了從未開發的組到探索組的距離,最短的距離。
特性
Back to Top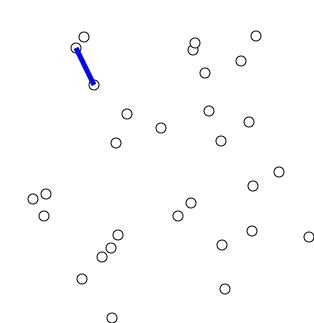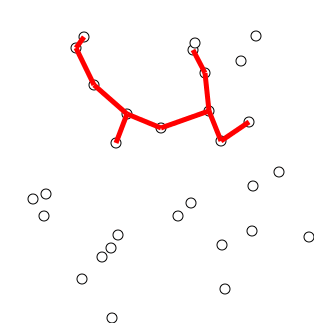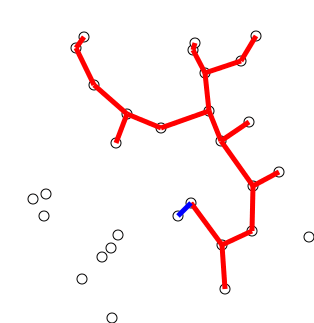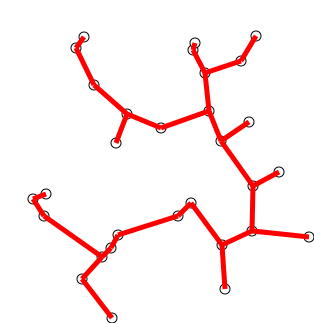
關鍵主意
該算法可以非正式地描述為執行以下步驟:
用單個頂點初始化樹,從圖形任意選擇。
通過一個邊來種植樹:將樹連接到樹上尚未在樹中的頂點的邊緣,找到最小重量的邊緣,然後將其轉移到樹上。
重複步驟2(直到所有頂點都在樹上)。
特性
Back to Top
關鍵主意
與SCC非常相似,我們可以儘早停止Alogrithm來控製圖中的類數,也就是說,我們可以將圖形聚集。
特性
Back to Top在本節中,我將介紹動態算法,這是一種強大的算法設計策略。
從維基百科(Wikipedia)來看,動態編程(也稱為動態優化)是一種通過將其分解為更簡單的子問題的集合,僅求解一次這些子問題並存儲解決方案來解決複雜問題。
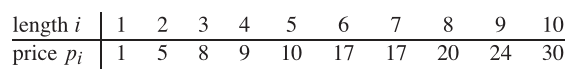
因此,如果桿的長度為8,並且給出不同零件的值如下,則最大可獲得的值為22(通過切成兩塊長度2和6的切割)。
關鍵主意
我們將分解視為由第一片長度組成,我切斷了左端,然後是長度為n-i的右手。因此,偽代碼看起來像:
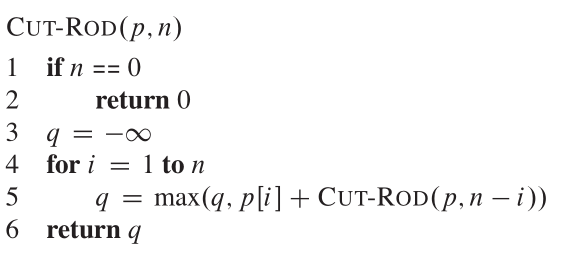
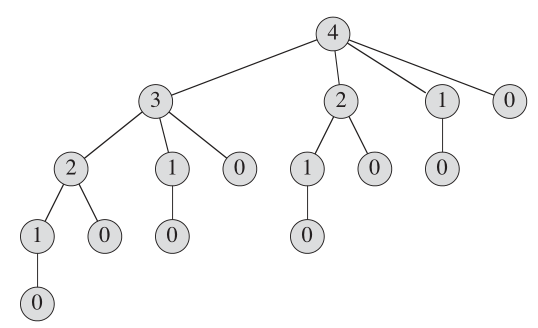
遞歸樹顯示由call cut_rod(p,n)產生的遞歸調用,看起來像:
為了節省小問題的重複計算,我們記住一個數組來存儲這些值。
特性
Back to Top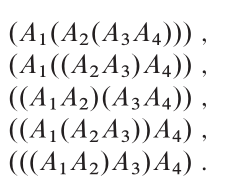
關鍵主意
最佳結構:
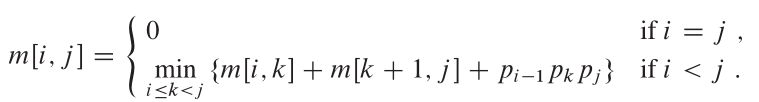
特性
Back to Top關鍵主意
從CLR中,此問題的最佳結構是:
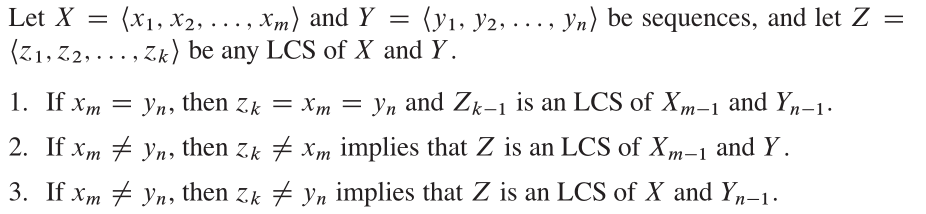
特性
Back to Top關鍵主意
該算法基於非常直觀的觀察。假設我們有一個子集{1,2,3,4,...,k}(表示為原始頂點組{1,2,3,...,n}的v(k)。如果p是從v(k)中的i到j的最短路徑,我們有兩種情況。首先,如果k不在p中,則p必須是v(k-1)中的最短路徑。其次,如果k在p中,那麼我們可以將路徑分為兩個,p1:i k,p2:k j。 P1必須是從i到K的最短路徑(K-1),P2必須是從K到J的最短路徑(K-1)。
特性
Back to Top從Wikipedia來看,NP完整的決策問題既屬於NP和NP-硬化的複雜性類別。在這種情況下,NP代表“非確定的多項式時間”。 NP Comperte問題集通常用NP-C或NPC表示。
在本節中,我將介紹三個非常著名的NPC問題,並解釋近似算法以接近它們。
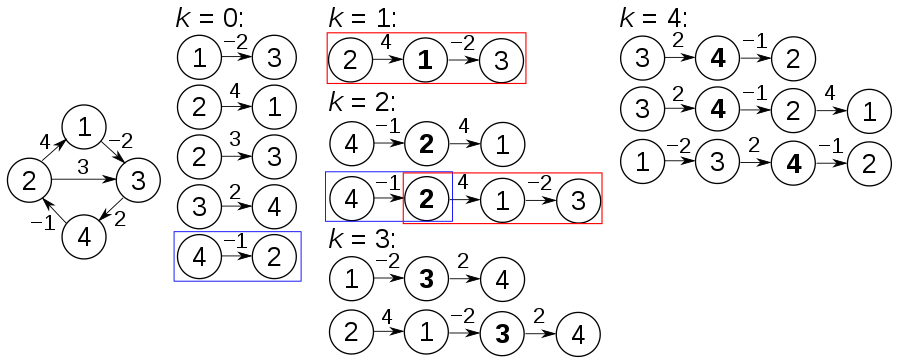
關鍵主意
很難找到最小頂點蓋,但是我們可以在多項式時間內找到最多兩倍的頂點蓋。

特性
Back to Top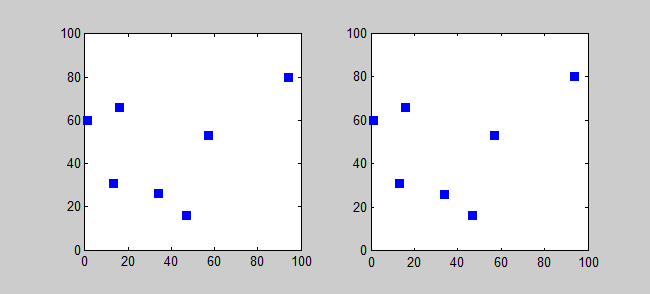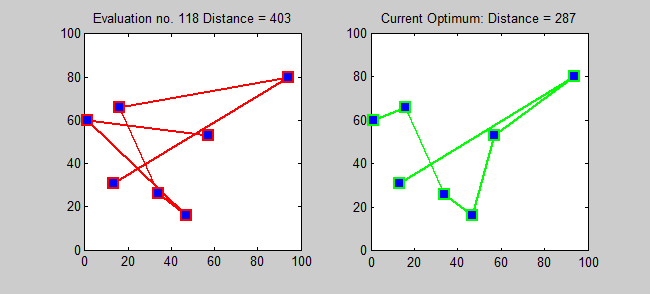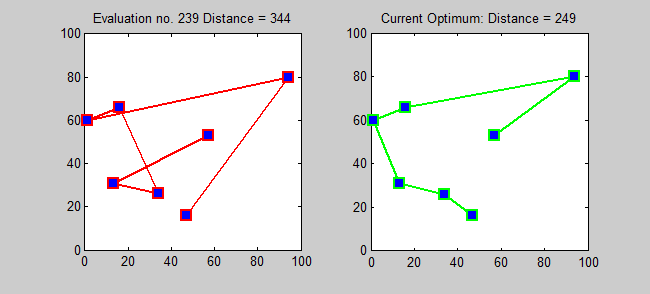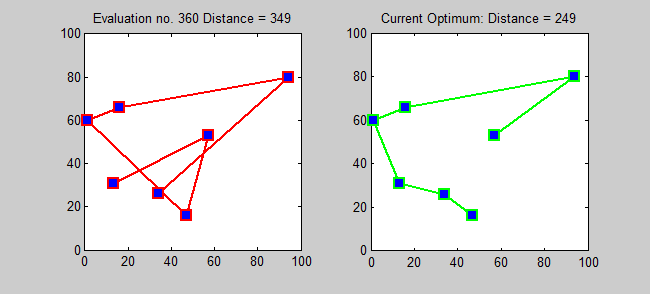
關鍵主意
TSP的近似算法是一種貪婪的算法(CLRS P1114)。在這裡,我還想使用動態編程為TSP介紹一種精確的算法。
子問題:對於每個目標j∈{1,2,...,n},每個子集s {1,2,...,n}包含1和j,讓ls,j =從1到j的路徑的最小長度,從1到j,確切地訪問了s的頂點[確切的每次[每次一次]]。因此,相應的複發:
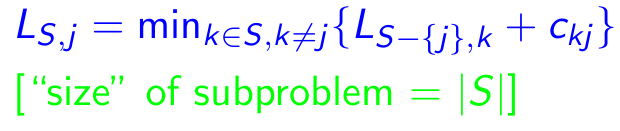
特性
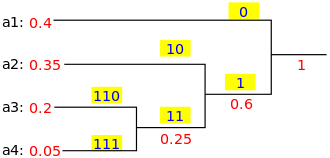
Back to Top 3-SAT是KARP的21個NP完整問題之一,它被用作證明其他問題也是NP-HARD的起點。
本文中,我介紹了2個SAT的Papadimitriou算法(這是一種非常非常非常有趣的算法,因此即使2-SAT不是NPC,我也決定將其介紹。
關鍵主意
選擇隨機的初始分配,然後選擇任意不滿意的子句,然後翻轉其變量之一的值。這是偽代碼:

這樣的隨意處理條款將使我們有很大的可能性找到真正的答案。該機制在於物理學術語(隨機步行)。如果您有興趣,我強烈建議您進行隨機步行與Papadimitriou的關係。
特性
Back to Top