In diesem Repository werde ich Python verwenden, um einige berühmte Algorithmen zu implementieren. Die Algorithmen sind gemäß der verwendeten Strategie angeordnet. Jeder Algorithmus hat eine Erklärung für das Problem, das er löst, und einige relevante Ressourcen.
(Das Ziel dieses Repositorys ist es, ein wunderschönes Readme für all diese brillanten Algorithmen zu erstellen, die ich überprüft habe.)
Inhalt:
In diesem Abschnitt werde ich über die berühmte Kluft- und Eroberungsstrategie sprechen und einige Anwendungen dieser Strategie zeigen.
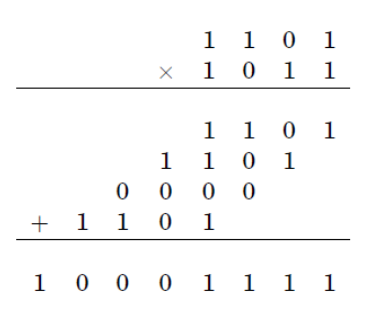
Das Standardverfahren zur Multiplikation zweier n-Digit-Zahlen erfordert eine Reihe von elementaren Operationen, die proportional sind. Der Karatsuba -Algorithmus verkürzt die Laufzeit höchstens
Schlüsselidee
Der grundlegende Schritt des Karatsuba -Algorithmus ist eine Formel, mit der man das Produkt zweier großer Zahlen berechnet und drei Multiplikationen kleinerer Zahlen verwendet, wobei jeweils etwa halb so viele Ziffern wie OD.
Eigenschaften
Back to Top
Die schlechteste Laufzeit für diesen Algorithmus ist.
GIF oben zeigt, wie die Zusammenführungssorte funktioniert: 
Schlüsselidee
Teilen Sie die unsortierte Liste in N -Unterverminderungen auf, die jeweils 1 Element enthält (eine Liste von 1 Element wird als sortiert angesehen) und verschmolzen immer wieder untervermüht, um neue sortierte Untervermieter zu produzieren, bis nur noch 1 Sublist verbleiben. Dies wird die sortierte Liste sein.
Eigenschaften
Back to Top
Schlüsselidee
Wenn wir wie in der obigen Abbildung das Element des rechten Unterarrays zum ersten Mal aus dem rechten Unterarray aufnehmen, ist dies an, dass das rechte Element kleiner als (Länge des linken Unterarrays-dem Index des linken Elements) Elemente ist.
Wenn der Algorithmus fortschreitet, geben wir alle Inversionen die Gesamtinversionen.
Eigenschaften
Back to Top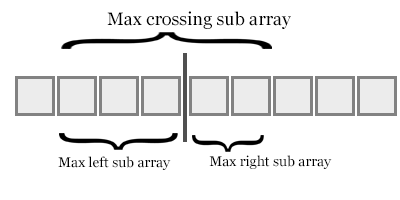
Eigenschaften
Back to TopIn diesem Abschnitt werde ich über zwei Algorithmen sprechen, die eine zufällige Variable im Inneren verwendet haben.
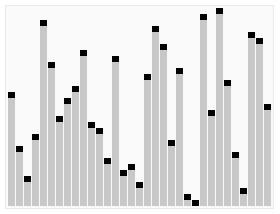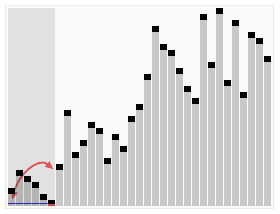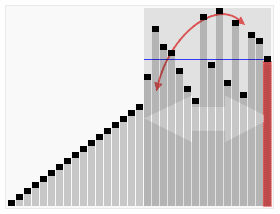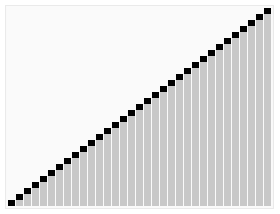
Schlüsselidee
Quicksort unterteilt zuerst ein großes Array in zwei kleinere Sub-Arrays: die niedrigen Elemente und die hohen Elemente im Vergleich zu einem zufällig ausgewählten Element. Quicksort kann dann die Sub-Arrays rekursiv sortieren. Der entscheidende Punkt in der schnellen Sortierung besteht also darin, ein Partitionselement zu wählen.
Eigenschaften
Back to Top
Schlüsselidee
Durch die Wiederholung der Kontraktionsalgorithmuszeiten mit unabhängigen zufälligen Entscheidungen und der Rückgabe des kleinsten Schnitts ist die Wahrscheinlichkeit, keinen Mindestschnitt zu finden
Eigenschaften
Back to TopDatenstrukturen als unabhängiger Abschnitt zu platzieren, ist irreführend. Ich werde jedoch verblüffende Probleme einführen, die elegant durch Datenstrukturen gelöst werden. Einige Datenstrukturen können eine Algorithmus -Designstrategie haben, die noch nicht überprüft wurde.
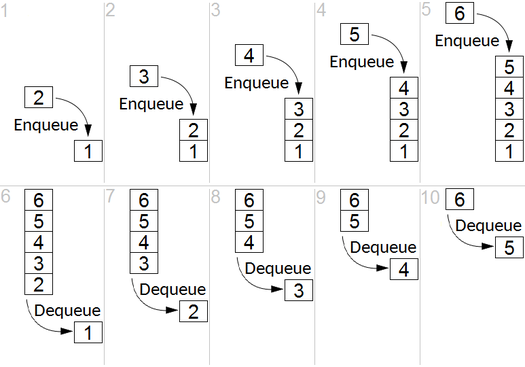
Schlüsselidee
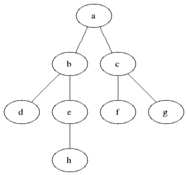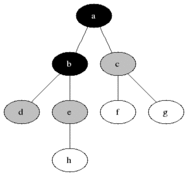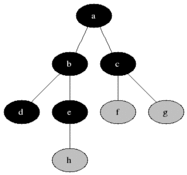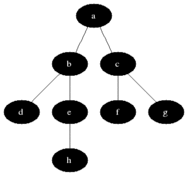
BFS wird verwendet, um erreichbare Knoten aus einem Quellknoten in einem ungerichteten oder gerichteten Diagramm zu zählen. In der gefundenen Reihenfolge sind erreichbare Knoten gedruckt. Eine Warteschlange wird verwendet, um die Knoten farbig grau zu speichern (siehe GIF unten). Der Begriff "Breite" in BFS bedeutet, einen erreichbaren Knoten mit kürzester Länge zu finden. Die Breite erweitert die Grenze zwischen den besuchten Knoten und den unentdeckten Knoten.
Eigenschaften
Back to Top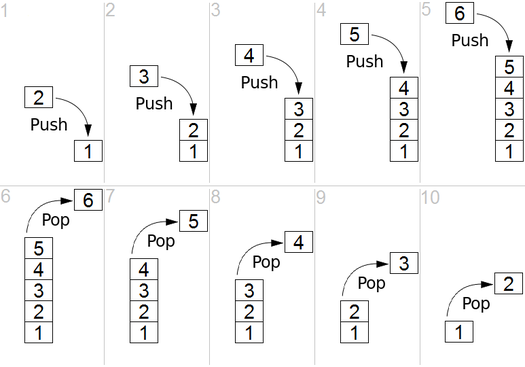
Schlüsselidee
Und DFS wird in einem gerichteten Diagramm verwendet und zeigt an, wie viele Knoten ein Quellknoten durch die Reihenfolge, die wir finden, erreichen und ausdrucken können. Wir verwenden Stack, um die Knoten zu speichern, die wir als Startpunkte für die Grafik klassifizieren. Die "Tiefe" in seinem Namen bedeutet, dass dieser Algorithmus so tief wie möglich für eine bestimmte Quelle verläuft und wenn er den Endpunkt erreicht, kehrt er zum Startknoten zurück.
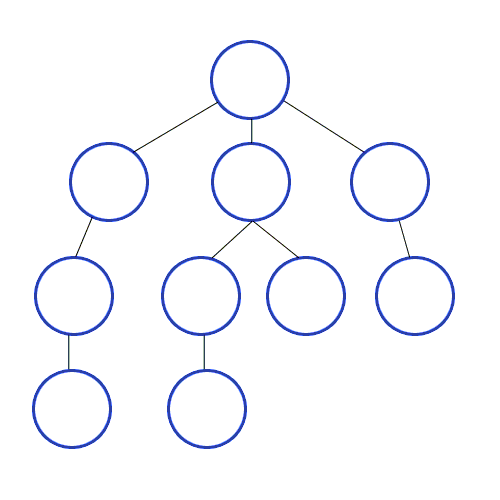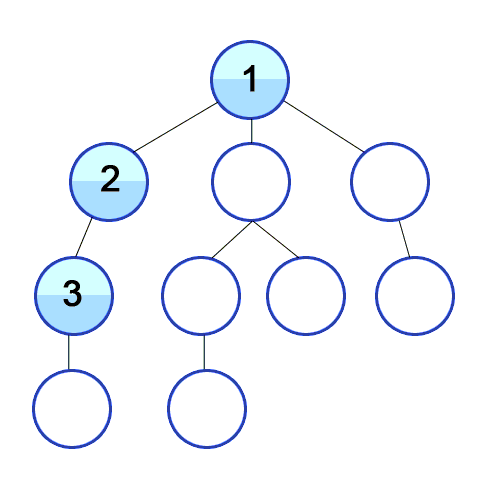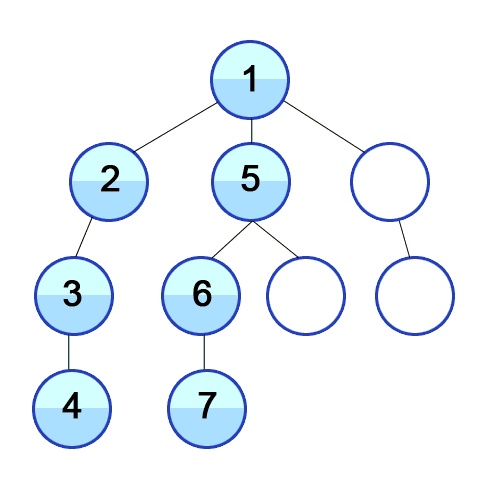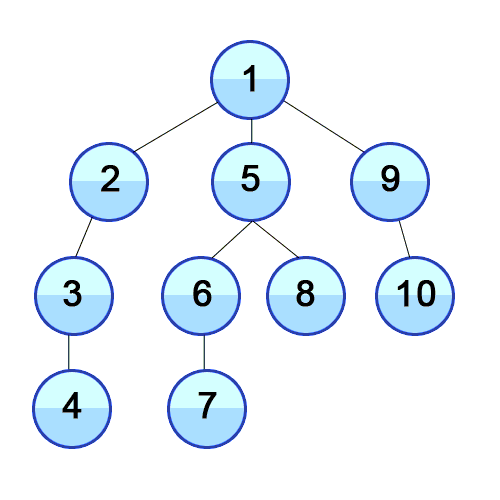
Eigenschaften
Back to Top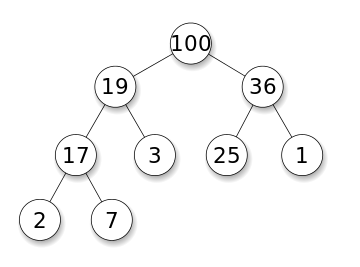
Das mediane Wartungsproblem besteht darin, dass Ganzzahlen aus einem Datenstrom ausgelesen werden, das Median der Elemente auf effiziente Weise gelesen hat. Der Einfachheit halber gehen davon aus, dass es keine Duplikate gibt.
Schlüsselidee
Wir können auf der linken Seite einen maximalen Haufen verwenden, um Elemente darzustellen, die weniger als effektiver Median sind, und einen minem Haufen auf der rechten Seite, um Elemente darzustellen, die größer sind als wirksamer Median. Wenn der Unterschied zwischen der Größe von zwei Haufen größer oder gleich 2 ist, wechseln wir ein Element auf einen anderen Haufen kleinerer Größe.
Eigenschaften
Back to Top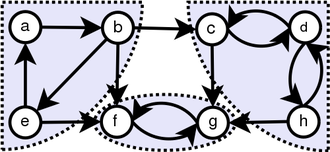
Schlüsselidee
Durch einfache Beobachtung finden wir heraus, dass Transierung des Diagramms die gleichen SCCs wie das Originalgraphen hat. Wir laufen zweimal DFS. Zum ersten Mal laufen wir auf G und berechnen die Endzeit für jeden Scheitelpunkt. Und dann laufen wir DFs auf g^t, aber in der Hauptschleife von DFS betrachten die Eckpunkte in der Reihenfolge der Abnahmezeit.
Eigenschaften
Back to Top
Schlüsselidee
In einem ungerichteten Diagramm können wir diese Datenstruktur verwenden, um herauszufinden, wie viele SCCs. Die folgende Abbildung zeigt, wie es funktioniert.
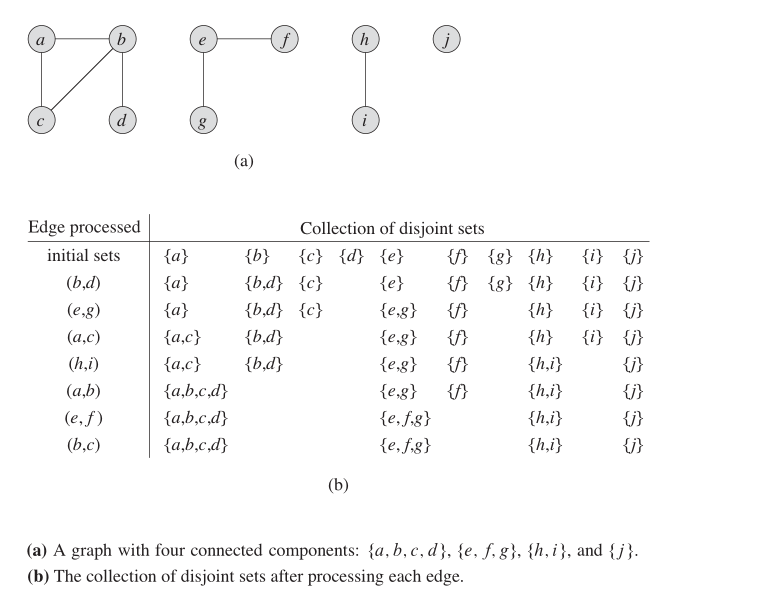
Eigenschaften
Back to Top In diesem Abschnitt werde ich gierige Algorithmen vorstellen, eine leistungsstarke Strategie zur Design von Algorithmus.
Aus Wikipedia ist ein gieriger Algorithmus ein algorithmisches Paradigma, das der Problemlösung folgt, um die lokal optimale Wahl in jeder Phase zu treffen [1] mit der Hoffnung, ein globales Optimum zu finden. In vielen Problemen führt eine gierige Strategie im Allgemeinen nicht zu einer optimalen Lösung, aber dennoch kann eine gierige Heuristik lokal optimale Lösungen erzeugen, die eine globale optimale Lösung in einer angemessenen Zeit annähern.
Bei der Auswahl des Aktivitätsauswahl hat jede Aktivität ihr eigenes Gewicht und ihre eigene Länge. Und unser Ziel ist es, die Summe des Gewichts*Länge zu minimieren. Es ist ein sehr einfaches und großartiges Beispiel zu zeigen, wie gieriger Algorithmus funktioniert und einen eleganten Beweis für die Argumentaustauschtechnik liefert.
Schlüsselidee
Wenn wir Aktivität nach Wertgewicht/Länge sortieren, können wir nachweisen, dass eine vorhandene optimale Struktur nicht besser sein kann als diese Anordnung. 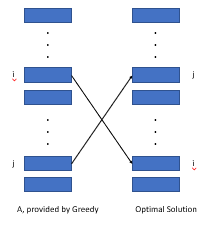
Wie die oben gezeigte Abbildung betrachten die Kosten, die durch zwei Aktivitäten verursacht werden, die in zwei Arrangements unterschiedlich entfernt sind (I, J). Wir finden heraus, dass die Kosten im gierigen Algorithmus durch den Wert von Wi*lj - wj*li, der größer oder gleich 0 ist, kleiner als die optimale Struktur sind.
Eigenschaften
Back to Top
Schlüsselidee
Wir haben das Array nach seiner Endzeit sortiert. Der Algorithmus hat den ersten Job gesetzt, dessen Startzeit größer ist als die Endzeit des letzten Jobs.
Eigenschaften
Back to Top
Eine Möglichkeit, dieses Buch zu codieren, besteht darin, die Codierung der festen Länge zu verwenden. Wie unten gezeigt:
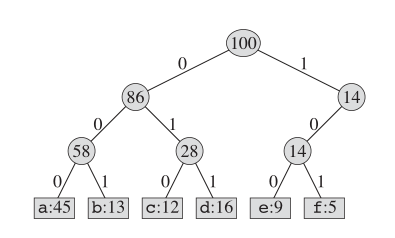
Was die Codierung von Huffman angeht, sieht die tatsächliche Baumstruktur so aus:
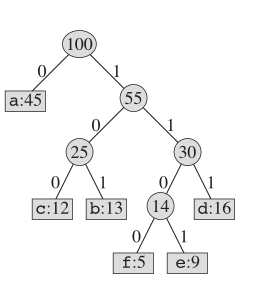
Schlüsselidee
Wir unterhalten einen binären Baum und erstellen einen neuen Knoten als Elternteil für zwei am wenigsten frequentierte Buchstaben. Und der Schlüssel für diesen neuen Knoten ist die Summe der Schlüssel für seine beiden Kinder. Wir wiederholen dies, bis keine Knoten in diesem "Buch" übrig sind.
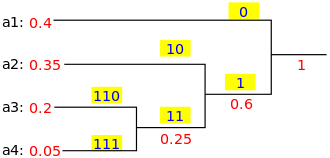
Eigenschaften
Back to TopDer Algorithmus von Dijkstra ist ein Algorithmus, um die kürzesten Pfade zwischen Knoten in einem Diagramm zu finden. Es hat jedoch eine Voraussetzung, alle Wege müssen größer oder gleich 0 sein.
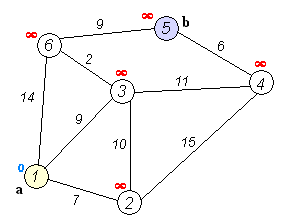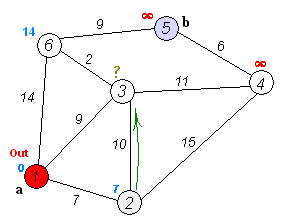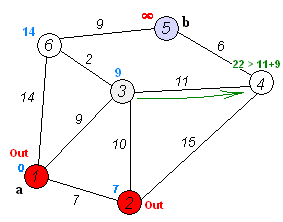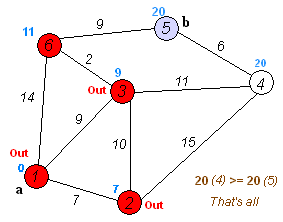
Schlüsselidee
Separate Knoten in zwei Gruppen ist eine Gruppe als untersucht markiert. Und wir aktualisieren die Entfernung von unerforschter Gruppe bis zur kürzesten Entfernung.
Eigenschaften
Back to Top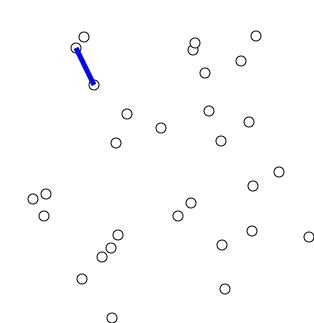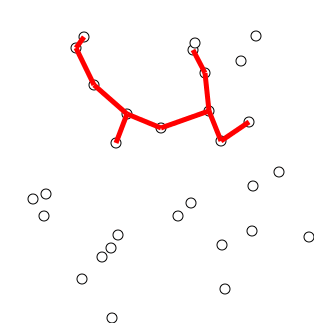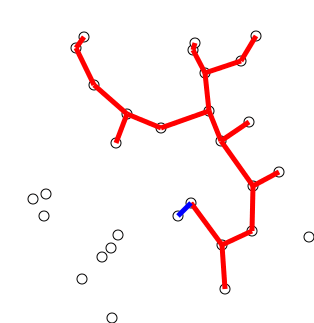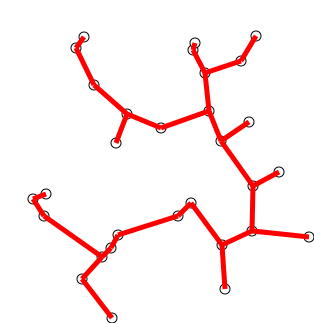
Schlüsselidee
Der Algorithmus kann informell als Ausführung der folgenden Schritte beschrieben werden:
Initialisieren Sie einen Baum mit einem einzelnen Scheitelpunkt, der willkürlich aus dem Diagramm ausgewählt wurde.
Wachsen Sie den Baum um eine Kante: der Kanten, die den Baum mit Scheitelpunkten verbinden, die noch nicht im Baum sind, finden Sie die minimale Kante und übertragen Sie ihn an den Baum.
Wiederholen Sie Schritt 2 (bis sich alle Scheitelpunkte im Baum befinden).
Eigenschaften
Back to Top
Schlüsselidee
Sehr ähnlich wie SCC, können wir den Alogrithmus frühzeitig stoppen, um die Anzahl der Klassen in unserem Diagramm zu steuern, dh wir können das Diagramm gruppieren.
Eigenschaften
Back to Top In diesem Abschnitt werde ich dynamische Algorithmen einführen, eine leistungsstarke Strategie für Algorithmus -Design.
Aus Wikipedia ist die dynamische Programmierung (auch als dynamische Optimierung bezeichnet) eine Methode zur Lösung eines komplexen Problems, indem es in eine Sammlung einfacherer Teilprobleme, die Lösung jeder dieser Unterprobleme nur einmal und die Speicherung ihrer Lösungen, zerlegt wird.
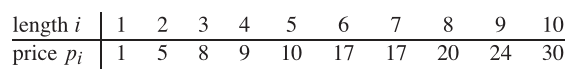
Wenn also die Länge der Stange 8 beträgt und die Werte verschiedener Teile wie folgt angegeben sind, beträgt der maximal erhältliche Wert 22 (durch Schneiden von zwei Längenstücken 2 und 6).
Schlüsselidee
Wir betrachten eine Zersetzung als aus einem ersten Stück Länge, das ich das linke Ende abgeschnitten habe, und dann einen rechten Rest der Länge n-i. Der Pseudocode sieht also aus wie:
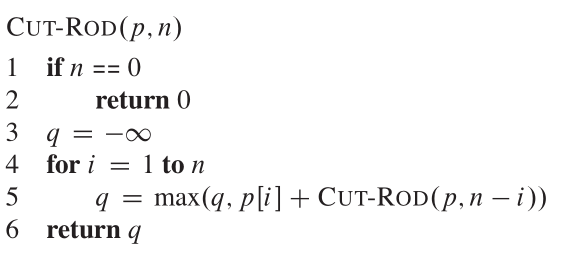
Der Rekursionsbaum zeigt rekursive Anrufe, die sich aus einem Call cut_rod (p, n) ergeben, sieht aus:
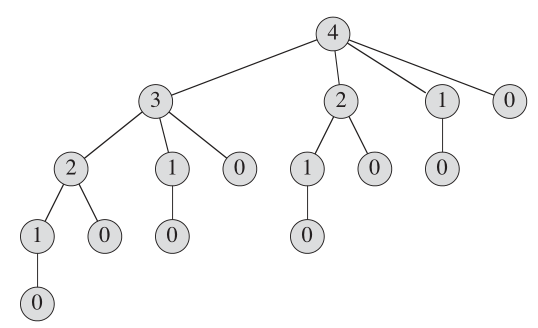
Um die wiederholte Berechnung für kleine Unterprobleme zu speichern, haben wir ein Array auswendig gelernt, um diese Werte zu speichern.
Eigenschaften
Back to Top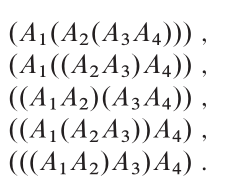
Schlüsselidee
Optimale Struktur:
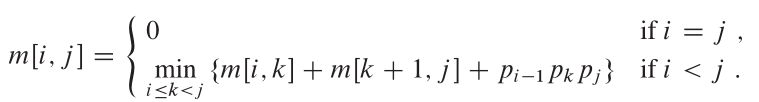
Eigenschaften
Back to Top Schlüsselidee
Aus CLRS ist die optimale Struktur für dieses Problem:
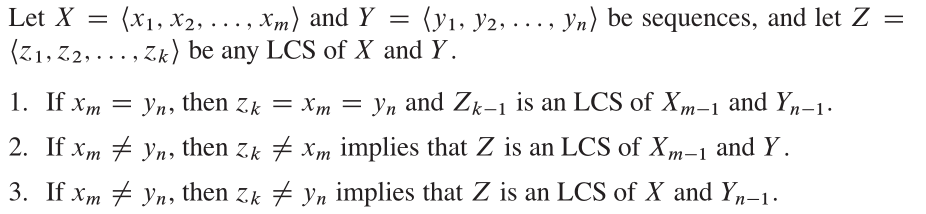
Eigenschaften
Back to Top Schlüsselidee
Dieser Algorithmus basiert auf sehr intuitiver Beobachtung. Angenommen, wir haben eine Untergruppe {1, 2, 3, 4, ..., k} (als v (k)) der ursprünglichen Eckpunktgruppe {1, 2, 3, ..., n}. Wenn p in V (k) ein kürzester Weg von i zu j ist, haben wir zwei Fälle. Wenn K nicht in P ist, muss P in V (k-1) ein kürzester Weg sein. Zweitens, wenn K in P ist, können wir den Pfad in zwei, p1: i k, p2: k J. und p1 muss der kürzeste Weg von i zu k mit V (k-1) sein, P2 muss der kürzeste Weg von k nach j mit V (k-1) sein.
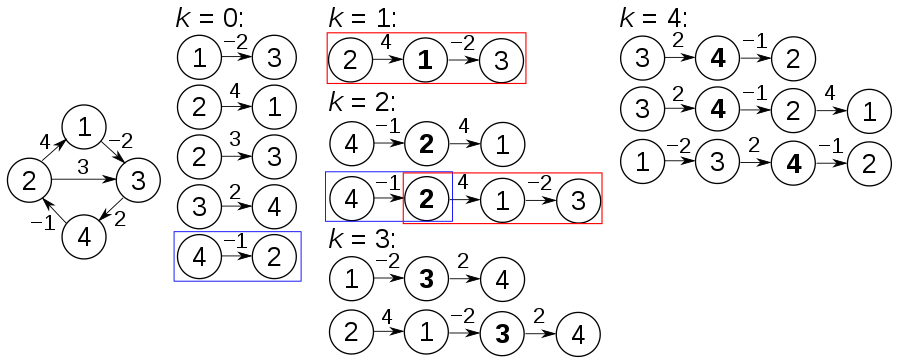
Eigenschaften
Back to Top Aus Wikipedia gehört ein NP-Complete-Entscheidungsproblem sowohl zum NP- als auch zum NP-HART-Komplexitätsklassen. In diesem Zusammenhang steht NP für "nicht deterministisches Polynomzeit". Der Satz von NP-Completen-Problemen wird häufig mit NP-C oder NPC bezeichnet.
In diesem Abschnitt werde ich drei sehr berühmte NPC -Probleme einführen und Annäherungsalgorithmen erläutern, um sich ihnen zu nähern.
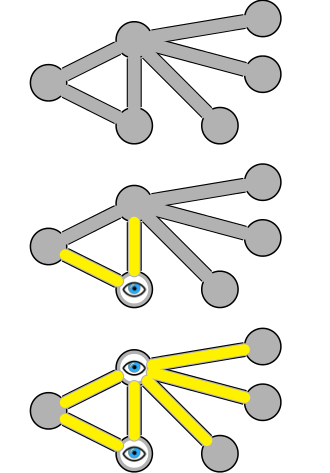
Schlüsselidee
Es ist sehr schwierig, eine minimale Scheitelpunktabdeckung zu finden, aber wir können eine ungefähre Abdeckung mit höchstens doppelten Scheitelpunkten in der Polynomzeit finden.

Eigenschaften
Back to Top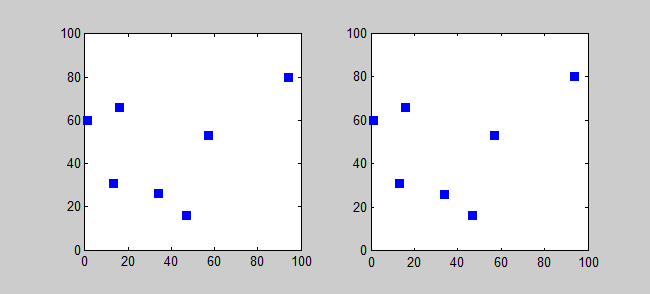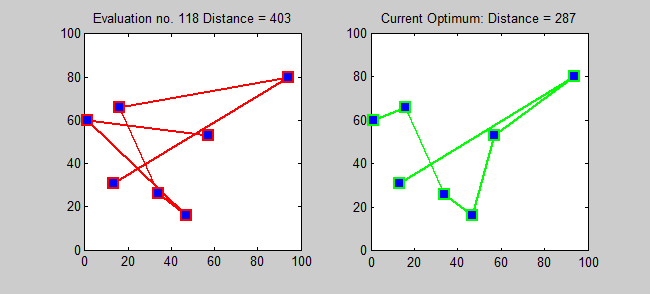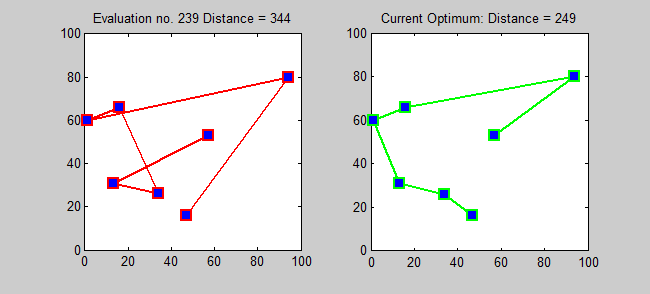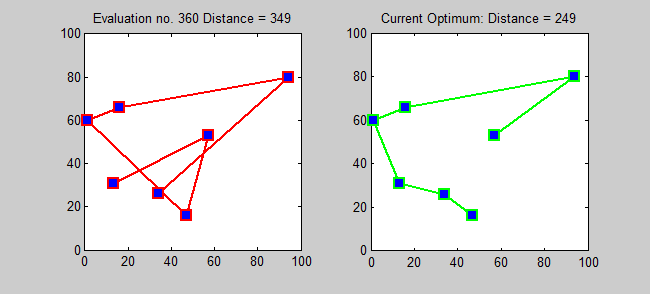
Schlüsselidee
Der Näherungsalgorithmus für TSP ist ein gieriger Algorithmus (CLRS P1114). Hier möchte ich auch einen genauen Algorithmus für TSP unter Verwendung einer dynamischen Programmierung einführen.
Subproblem: Für jedes Ziel j ∈ {1,2, ..., n}, jede Teilmenge s ⊆ {1,2, ..., n}, die 1 und j, lass ls, j = minimale Länge eines Pfades von 1 zu j enthält, der genau die Scheitelpunkte von s [genau einmal] besucht. Also entsprechende Wiederauftreten:
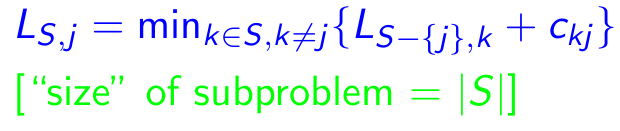
Eigenschaften
Back to Top 3-sa ist eines der 21 NP-Vervollständigung von Karp und es wird als Ausgangspunkt für den Beweis verwendet, dass auch andere Probleme NP-HARD sind.
Hier stelle ich Papadimitrius Algorithmus für 2-SAT vor (dies ist ein sehr, sehr interessanter Algorithmus , also entscheide ich mich, ihn vorzustellen, obwohl 2-sat kein NPC ist).
Schlüsselidee
Wählen Sie zufällige anfängliche Zuordnung und wählen Sie willkürliche unzufriedene Klausel und drehen Sie den Wert einer seiner Variablen um. Hier ist der Pseudocode:

Ein solcher ungezwungener Umgang mit Klauseln würde uns überraschenderweise eine sehr große Wahrscheinlichkeit geben, die wirkliche Antwort zu finden. Der Mechanismus liegt in einem Physikbegriff (Zufalls Walk). Wenn Sie interessiert sind, empfehle ich Ihnen dringend, zu gehen, wie der zufällige Spaziergang mit Papadimitriou in Verbindung steht.
Eigenschaften
Back to Top