이 저장소에서는 파이썬을 사용하여 유명한 알고리즘을 구현합니다. 알고리즘은 사용 된 전략에 따라 배열됩니다. 각 알고리즘은 해결하려는 문제와 관련 리소스에 대한 설명이 있습니다.
(이 저장소의 목표는 내가 검토 한 모든 훌륭한 알고리즘에 대한 아름다운 읽기를 만드는 것입니다.)
콘텐츠:
이 섹션에서는 유명한 분열 및 정복 전략에 대해 이야기 하고이 전략의 일부 응용 프로그램을 보여 드리겠습니다.
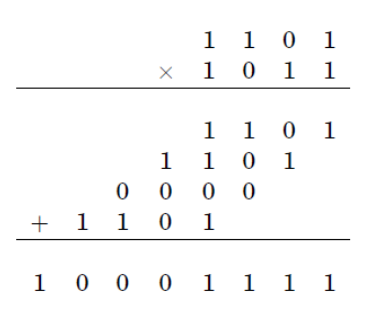
두 개의 n 자리 수의 곱셈을위한 표준 절차는 비례 비례에 비례하여 다수의 기본 작업이 필요합니다. Karatsuba 알고리즘은 실행 시간을 최대로 줄입니다.
핵심 아이디어
Karatsuba 알고리즘의 기본 단계는 두 개의 많은 숫자의 곱을 계산하고 작은 숫자의 세 가지 곱셈을 사용하여 각각 약 절반 정도의 숫자와 일부 추가 및 숫자 교대를 사용하는 공식입니다.
속성
Back to Top
이 알고리즘의 최악의 실행 시간은입니다.
위의 GIF는 Merge 정렬의 작동 방식을 보여줍니다. 
핵심 아이디어
분류되지 않은 목록을 n 하위 목록으로 나누고 각각 1 개의 요소 (1 요소 목록은 분류 된 것으로 간주 됨)를 포함하고 하위 목록을 반복적으로 병합하여 1 개의 하위리스트가 남아있을 때까지 새로운 분류 된 하위리스트를 생성합니다. 이것은 정렬 된 목록이 될 것입니다.
속성
Back to Top
핵심 아이디어
위의 그림과 마찬가지로 Merge 작동에서 오른쪽 서브 어레이에서 요소를 처음 가져 오면 오른쪽 요소가 (왼쪽 서브 어레이의 길이-왼쪽 요소의 인덱스) 요소보다 작음을 나타냅니다.
알고리즘이 진행됨에 따라 모든 역전을 추가하면 전체 반전이 제공됩니다.
속성
Back to Top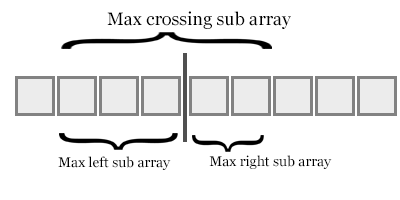
속성
Back to Top이 섹션에서는 임의의 변수를 내부에 사용한 두 가지 알고리즘에 대해 이야기하겠습니다.
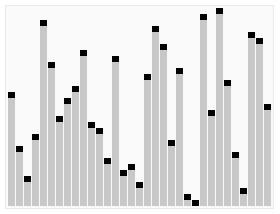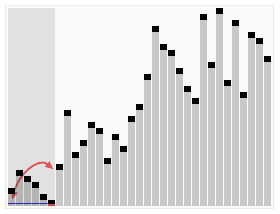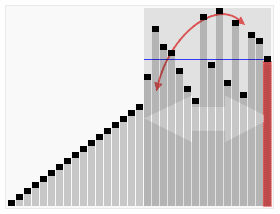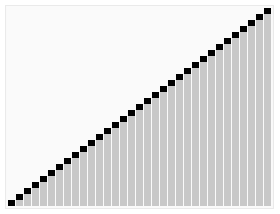
핵심 아이디어
QuickSort는 먼저 큰 배열을 두 개의 작은 하위 배열로 나눕니다 : 낮은 요소와 무작위로 선택된 요소에 대한 높은 요소. 그런 다음 QuickSort는 하위 배열을 재귀 적으로 정렬 할 수 있습니다. 따라서 빠른 정렬의 핵심 사항은 파티션 요소를 선택하는 것입니다.
속성
Back to Top
핵심 아이디어
독립적 인 임의의 선택으로 수축 알고리즘 시간을 반복하고 가장 작은 컷을 반환함으로써 최소 컷을 찾지 못할 확률은 다음과 같습니다.
속성
Back to Top데이터 구조를 독립적 인 섹션으로 배치하는 것은 오해의 소지가 있습니다. 그러나 데이터 구조에 의해 우아하게 해결되는 당황한 문제를 소개 할 것입니다. 일부 데이터 구조에는 아직 검토되지 않은 알고리즘 설계 전략이있을 수 있습니다.
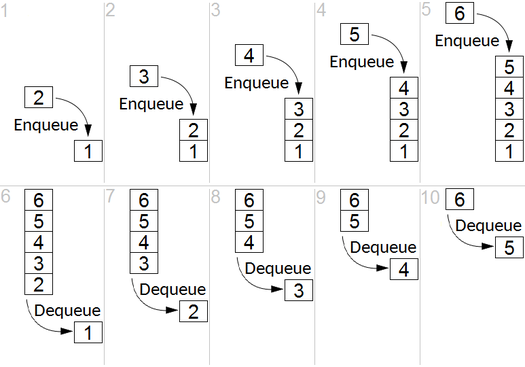
핵심 아이디어
BFS는 방향 또는 지시되지 않은 그래프의 소스 노드에서 도달 가능한 노드를 계산하는 데 사용됩니다. 도달 가능한 노드는 찾은 순서로 인쇄됩니다. 대기열은 노드 색상 회색을 저장하는 데 사용됩니다 (아래 GIF 참조). BFS에서 "폭"이라는 용어는 길이가 가장 짧은 도달 가능한 노드를 찾는 것을 의미합니다. 폭은 방문한 노드와 발견되지 않은 노드 사이의 경계를 연장합니다.
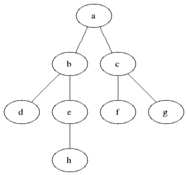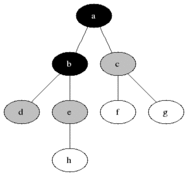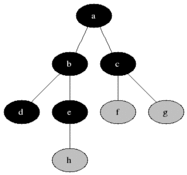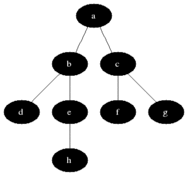
속성
Back to Top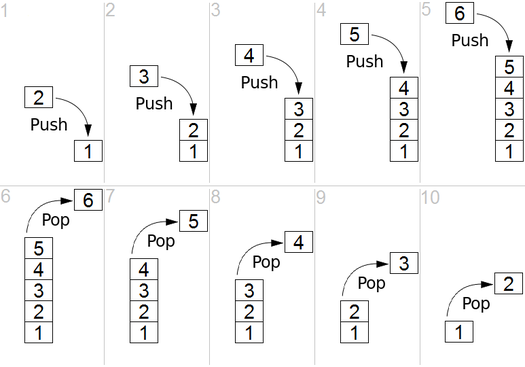
핵심 아이디어
DFS는 지시 된 그래프에서 사용되며 소스 노드가 도달 할 수있는 노드 수를 알려줍니다. 스택을 사용하여 그래프의 시작점으로 분류하는 노드를 저장합니다. 이름의 "깊이"는이 알고리즘이 주어진 소스에 대해 가능한 한 깊이 진행되며 종말점에 도달하면 시작 노드로 돌아옵니다.
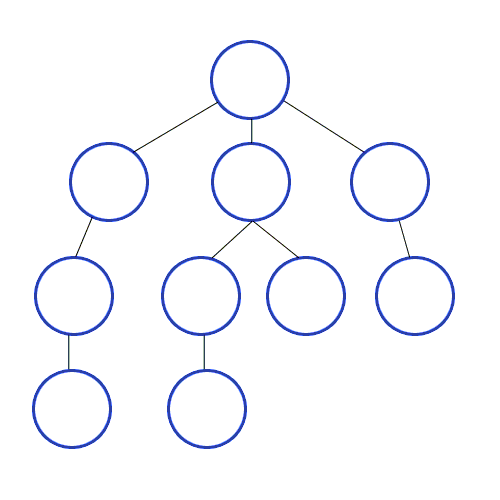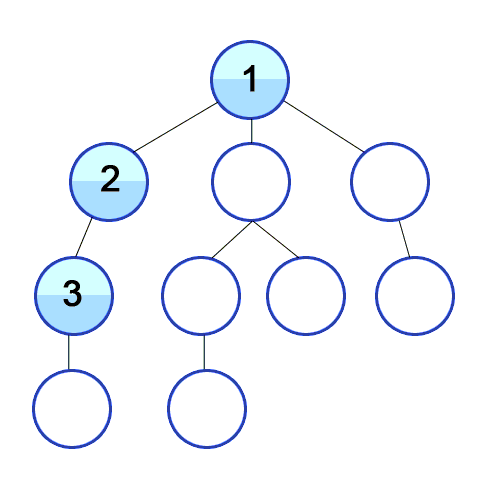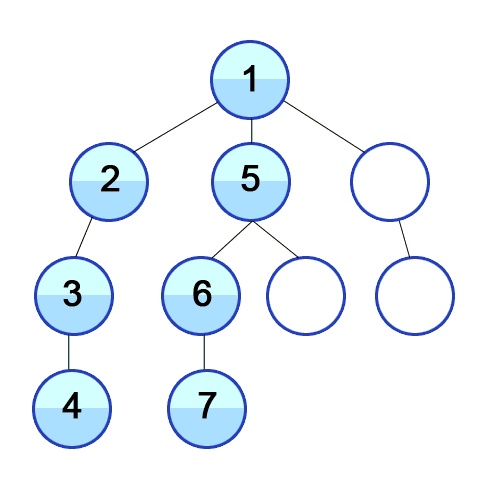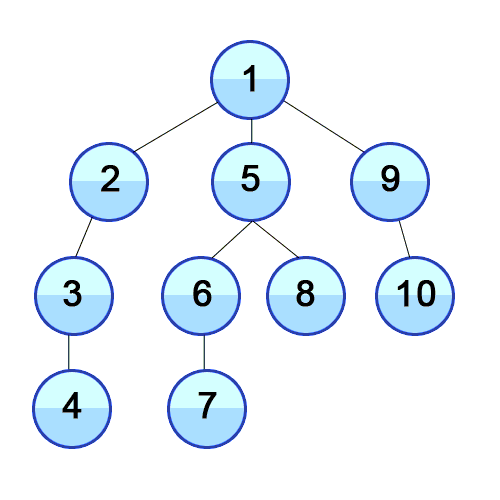
속성
Back to Top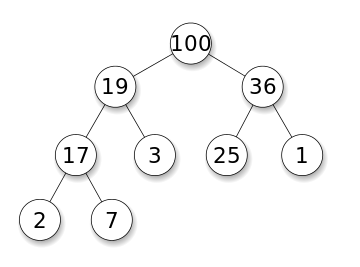
중간 유지 보수 문제는 정수가 데이터 스트림에서 읽히면 효율적인 방법으로 요소 중앙값을 읽는다는 것입니다. 단순성을 위해 중복이 없다고 가정합니다.
핵심 아이디어
우리는 왼쪽의 최대 힙을 사용하여 유효 중앙값보다 적은 요소와 오른쪽의 최소 힙을 사용하여 효과적인 중앙값보다 큰 요소를 나타낼 수 있습니다. 두 힙의 크기 사이의 차이가 2 인 경우, 하나의 요소를 다른 작은 크기 힙으로 전환합니다.
속성
Back to Top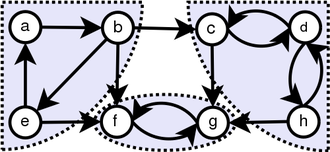
핵심 아이디어
간단한 관찰을 통해, 우리는 Tranpose of Graph가 원래 그래프와 동일한 SCC를 가지고 있음을 알 수 있습니다. 우리는 DFS를 두 번 실행합니다. 처음으로 G에서 실행하고 각 정점에 대한 마무리 시간을 계산합니다. 그런 다음 G^T에서 DFS를 실행하지만 DFS의 주요 루프에서는 마무리 시간을 줄이기 위해 정점을 고려하십시오.
속성
Back to Top
핵심 아이디어
방지 그래프 에서이 데이터 구조를 사용하여 SCC의 수를 찾을 수 있습니다. 아래 그림은 작동 방식을 보여줍니다.
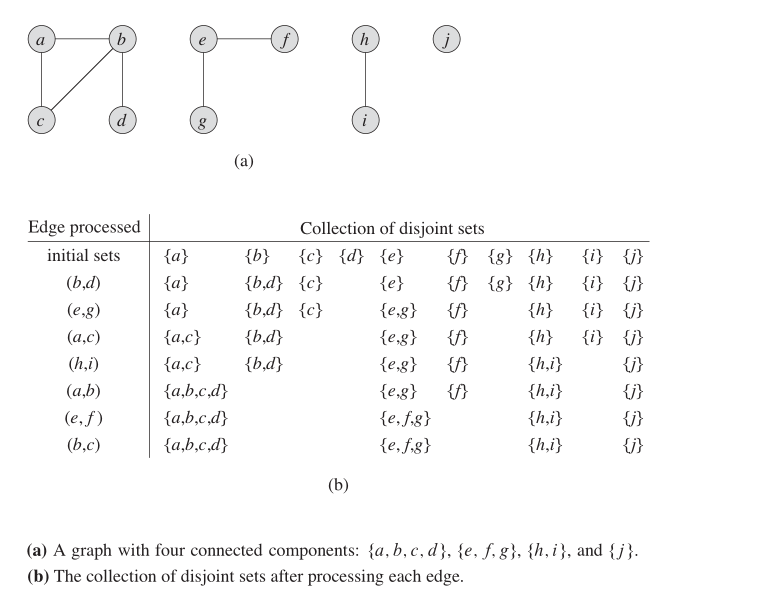
속성
Back to Top 이 섹션에서는 강력한 알고리즘 설계 전략 인 Greedy 알고리즘을 소개 할 것입니다.
Wikipedia에서 Greedy 알고리즘은 전 세계 최적을 찾기 위해 각 단계에서 로컬로 최적의 선택을하는 데 문제를 해결하는 문제를 해결하는 문제를 따르는 알고리즘 패러다임입니다. 많은 문제에서 탐욕스러운 전략은 일반적으로 최적의 솔루션을 생성하지는 않지만 그럼에도 불구하고 탐욕스러운 휴리스틱은 합리적인 시간에 글로벌 최적 솔루션을 근사화하는 로컬 최적의 솔루션을 생성 할 수 있습니다.
활동 선택 문제에서 모든 활동에는 자체 무게와 길이가 있습니다. 그리고 우리의 목표는 무게*길이의 합을 최소화하는 것입니다. 욕심 많은 알고리즘이 어떻게 작동하는지 보여주고 인수 교환 기술을 사용하여 우아한 증거를 제공하는 것은 매우 쉽고 훌륭한 예입니다.
핵심 아이디어
가치 가중/길이별로 활동을 분류하면 기존 최적의 구조 가이 배열보다 더 나을 수 없다는 것을 증명할 수 있습니다. 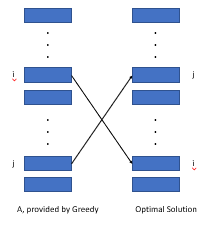
위에서 볼 수 있듯이, 우리는 두 가지 배열 (i, j)에서 다르게 범위 된 두 가지 활동으로 인한 비용을 고려합니다. 욕심 많은 알고리즘의 비용은 Wi*lj -wj*li의 값에 의해 최적의 구조보다 작다는 것을 알 수 있습니다.
속성
Back to Top
핵심 아이디어
마무리 시간에 따라 배열을 정렬했습니다. 알고리즘은 시작 시간이 마지막 작업의 마무리 시간보다 큰 첫 번째 작업을합니다.
속성
Back to Top
이 책을 인코딩하는 한 가지 방법은 고정 길이 코딩을 사용하는 것입니다. 아래 그림과 같이 :
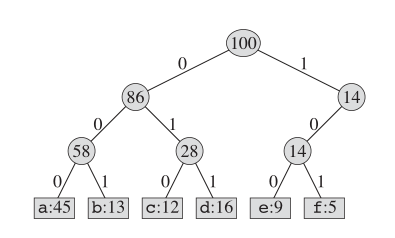
허프만 코딩의 경우 실제 트리 구조는 다음과 같습니다.
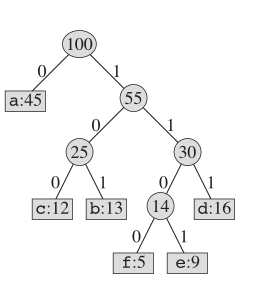
핵심 아이디어
우리는 이진 트리를 유지하고 두 개의 가장 부지런한 문자에 대한 부모로서 새 노드를 만듭니다. 이 새 노드의 핵심은 두 자녀의 키의 합입니다. 우리는이 "책"에 남은 노드가 남지 않을 때까지 이것을 반복합니다.
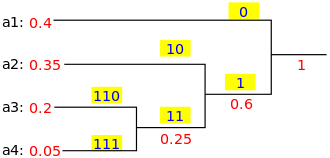
속성
Back to Topdijkstra의 알고리즘은 그래프에서 노드들 사이에서 가장 짧은 경로를 찾기위한 알고리즘입니다. 그러나 하나의 전제 조건이 있으며 모든 경로는 0이어야합니다.
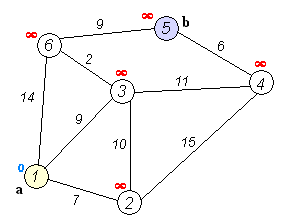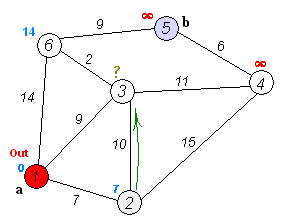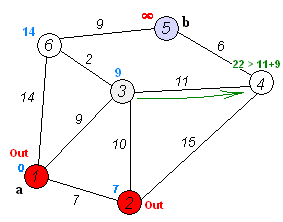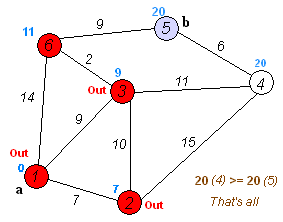
핵심 아이디어
별도의 노드는 두 그룹으로, 한 그룹은 탐색 된 것으로 표시됩니다. 그리고 우리는 탐험되지 않은 그룹에서 탐색 된 그룹까지의 거리를 가장 짧은 거리까지 업데이트합니다.
속성
Back to Top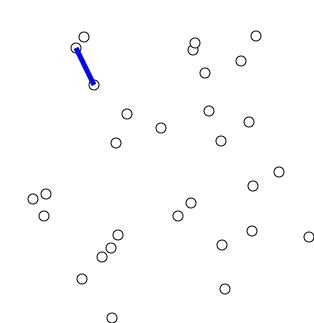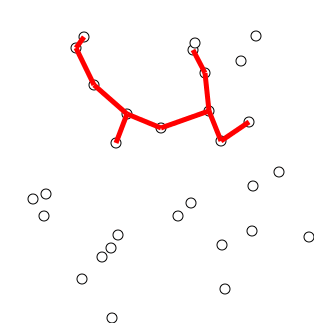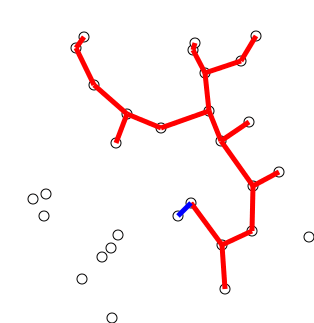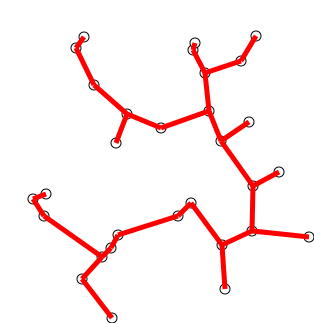
핵심 아이디어
알고리즘은 비공식적으로 다음 단계를 수행하는 것으로 설명 될 수 있습니다.
그래프에서 임의로 선택한 단일 정점으로 트리를 초기화하십시오.
나무를 아직 나무에 포함하지 않은 정점에 연결하는 가장자리의 한쪽 가장자리 씩 나무를 키우고 최소 체중 가장자리를 찾아 나무로 옮깁니다.
2 단계를 반복하십시오 (모든 정점이 나무에있을 때까지).
속성
Back to Top
핵심 아이디어
SCC와 매우 유사하게, 우리는 Alogrithm을 조기 중지하여 그래프에서 클래스 수를 제어 할 수 있습니다. 즉, 그래프를 클러스터링 할 수 있습니다.
속성
Back to Top 이 섹션에서는 하나의 강력한 알고리즘 설계 전략 인 동적 알고리즘을 소개하겠습니다.
Wikipedia에서 Dynamic Programming (Dynamic Optimization이라고도 함)은 복잡한 문제를 해결하여 간단한 하위 문제를 해결하고 각 하위 문제를 한 번만 해결하고 솔루션을 저장하는 방법입니다.
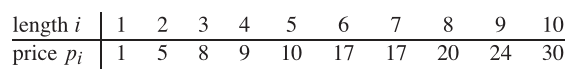
따라서로드의 길이가 8이고 다른 조각의 값이 다음과 같이 주어지면 최대 획득 가능한 값은 22입니다 (길이 2와 6의 두 조각으로 절단 함).
핵심 아이디어
우리는 왼쪽 끝을 차단 한 첫 번째 길이의 길이로 구성된 다음 길이 n-i의 오른쪽 나머지로 구성된 것으로 분해를 본다. 따라서 의사 코드는 다음과 같습니다.
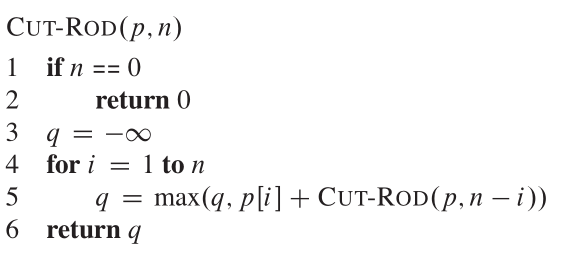
Call Cut_Rod (P, N)로 인한 재귀 호출을 보여주는 재귀 트리는 다음과 같습니다.
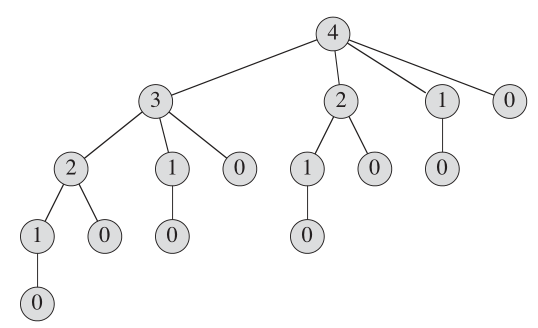
작은 하위 프로젝트에 대한 반복 계산을 저장하기 위해 이러한 값을 저장하는 배열을 암기했습니다.
속성
Back to Top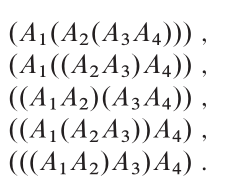
핵심 아이디어
최적의 구조 :
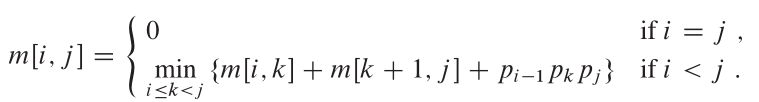
속성
Back to Top 핵심 아이디어
CLRS 에서이 문제에 대한 최적의 구조는 다음과 같습니다.
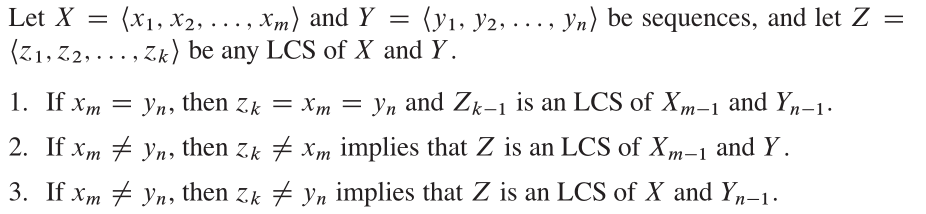
속성
Back to Top 핵심 아이디어
이 알고리즘은 매우 직관적 인 관찰을 기반으로합니다. 원래 정점 그룹 {1, 2, 3, ..., n}의 서브 세트 {1, 2, 3, 4, ..., k} (v (k)로 표시)가 있다고 가정합니다. p가 v (k)에서 i에서 J로 가장 짧은 경로 인 경우 두 가지 경우가 있습니다. 첫째, k가 p에 있지 않으면 p (k-1)에서 가장 짧은 경로 여야합니다. 둘째, k가 p에 있다면, 우리는 경로를 둘로 분리 할 수 있습니다. p1 : i K, P2 : k J. P1은 V (K-1)를 사용하여 I에서 K에서 K로 가장 짧은 경로 여야하며, p2는 v (k-1)를 사용하여 k에서 j까지 가장 짧은 경로 여야합니다.
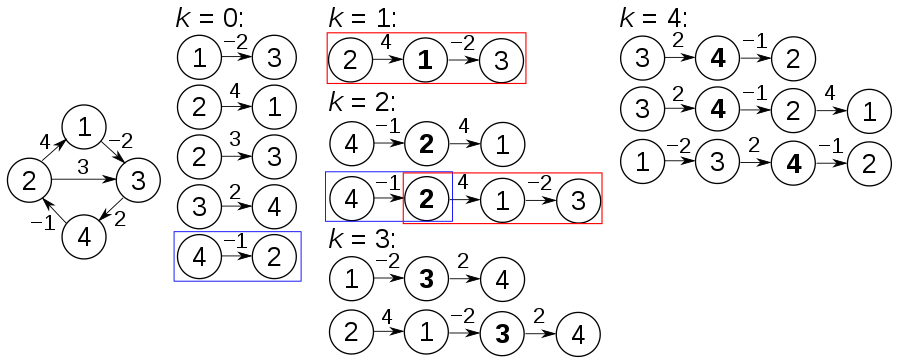
속성
Back to Top Wikipedia에서 NP- 완료 결정 문제는 NP 및 NP-HARD 복잡성 클래스 모두에 속하는 문제입니다. 이러한 맥락에서, NP는 "비 결정적 다항식 시간"을 나타냅니다. NP- 완료 문제의 세트는 종종 NP-C 또는 NPC로 표시됩니다.
이 섹션에서는 세 가지 매우 유명한 NPC 문제를 소개하고 근사 알고리즘을 설명하여 접근 할 것입니다.
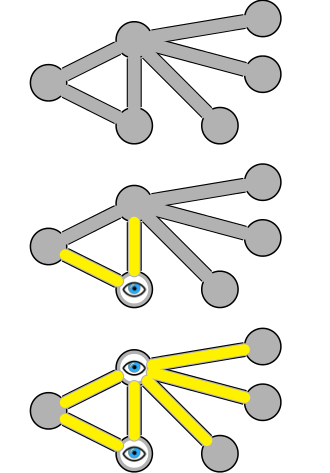
핵심 아이디어
최소 정점 덮개를 찾는 것은 매우 어렵지만 다항식 시간에 정점의 최대 두 배인 대략적인 덮개를 찾을 수 있습니다.

속성
Back to Top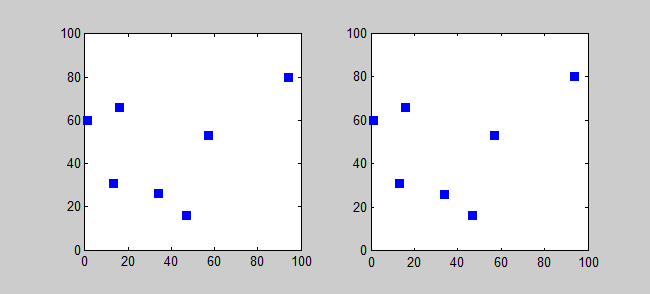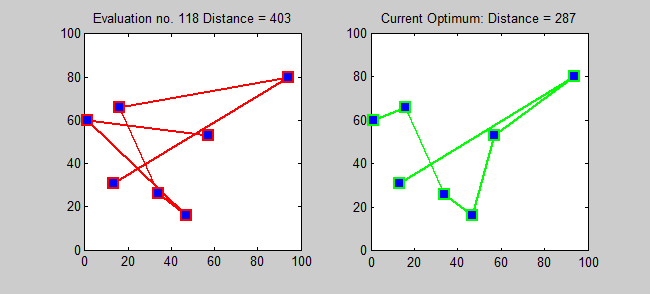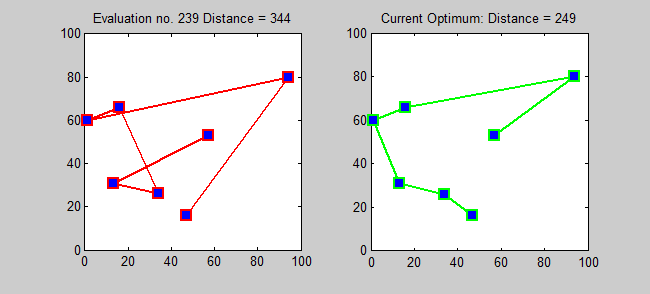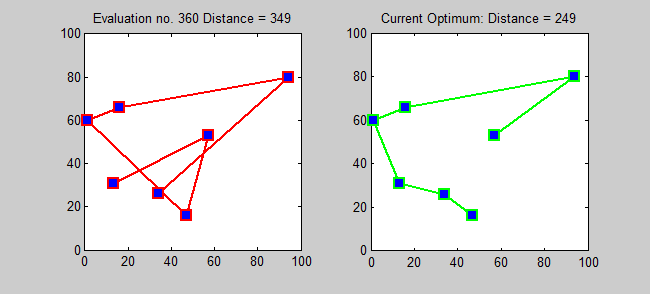
핵심 아이디어
TSP의 근사 알고리즘은 탐욕스러운 알고리즘입니다 (CLRS P1114). 여기서도 동적 프로그래밍을 사용하여 TSP에 대한 정확한 알고리즘을 소개하고 싶습니다.
하위 문제 : 모든 대상 J ∈ {1,2, ..., n}에 대해, 1과 j를 포함하는 모든 서브 세트 S ⊆ {1,2, ..., n}, ls, j = 1에서 j까지의 경로의 최소 길이를 정확하게 방문하는 s [정확히 한 번 각각]. 따라서 해당 재발 :
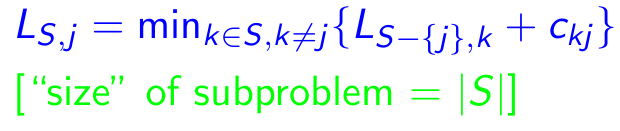
속성
Back to Top 3-SAT는 KARP의 21 NP 완료 문제 중 하나이며 다른 문제도 NP-HARD임을 입증하기위한 출발점으로 사용됩니다.
여기에서는 2-SAT에 대한 Papadimitriou 알고리즘을 소개합니다 (이것은 매우 흥미로운 알고리즘 이므로 2-SAT가 NPC가 아니더라도 소개하기로 결정합니다).
핵심 아이디어
임의의 초기 할당을 선택하고 임의의 불만족 조항을 선택하고 변수 중 하나의 값을 뒤집습니다. 여기 유사 코드는 다음과 같습니다.

조항을 다루는 그러한 캐주얼은 우리에게 실제 답변을 찾을 확률을 매우 많이 줄 것입니다. 메커니즘은 물리 용어 (임의의 산책)에 있습니다. 관심이 있으시면 Papadimitriou와 관련된 임의의 산책을 강력히 추천합니다.
속성
Back to Top