هذا المستودع ، سأستخدم Python لتنفيذ بعض الخوارزميات الشهيرة. يتم ترتيب الخوارزميات وفقًا للاستراتيجية المستخدمة. سيكون لكل خوارزمية تفسير للمشكلة التي تحاول حلها وبعض الموارد ذات الصلة.
(الهدف من هذا المستودع هو إنشاء عملية إعادة صياغة جميلة لجميع هذه الخوارزميات الرائعة التي قمت بمراجعتها.)
محتوى:
هذا القسم ، سأتحدث عن استراتيجية الفجوة والقهر الشهيرة وأظهر بعض تطبيقات هذه الاستراتيجية.
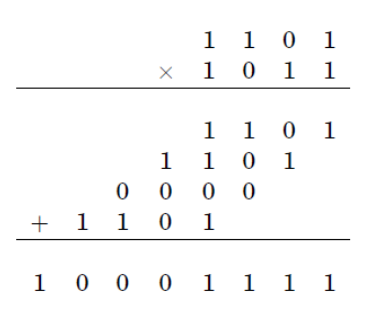
يتطلب الإجراء القياسي لضرب رقمين من الرقمين عددًا من العمليات الأولية التي تتناسب مع. أما بالنسبة لخوارزمية Karatsuba ، فإنها تقلل من وقت التشغيل إلى معظم
الفكرة الرئيسية
الخطوة الأساسية لخوارزمية Karatsuba هي صيغة تسمح للمرء بحساب منتج اثنين من الأرقام الكبيرة واستخدام ثلاثة مضاعفات من الأرقام الأصغر ، ولكل منها حوالي نصف الأرقام أو ، بالإضافة إلى بعض الإضافات وتحولات الأرقام.
ملكيات
Back to Top
أسوأ وقت تشغيل لهذه الخوارزمية هو.
توضح GIF أعلاه كيف يعمل Serge Sort: 
الفكرة الرئيسية
قسّم القائمة غير المصنفة إلى قوائم فرعية N ، كل عنصر يحتوي على عنصر واحد (يتم اعتبار قائمة عنصر واحد مرتبة) ودمج القواعد الفرعية مرارًا وتكرارًا لإنتاج القواعد الفرعية المصنفة الجديدة حتى لا يتبقى سوى أحد القاتمين الفرعيين. ستكون هذه هي القائمة المرتبة.
ملكيات
Back to Top
الفكرة الرئيسية
مثل الشكل أعلاه ، عندما نأخذ عنصرًا من العناصر الفرعية اليمنى في عملية الدمج ، يشير إلى أن العنصر الأيمن أصغر من (طول المباراة الفرعية اليسرى-فهرس العناصر اليسرى).
مع تقدم الخوارزمية ، أضف جميع الانقلابات سوف تعطينا الانقلابات الكلية.
ملكيات
Back to Top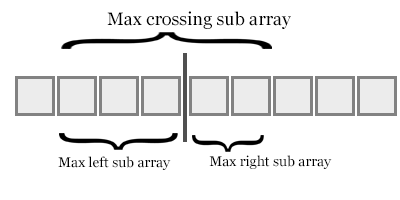
ملكيات
Back to Topسأتحدث عن هذا القسم عن خوارزميات استخدمت متغيرًا عشوائيًا في الداخل.
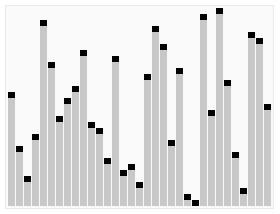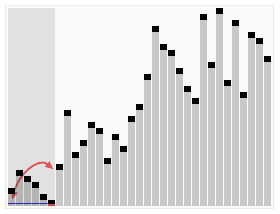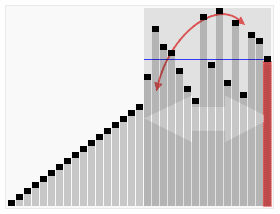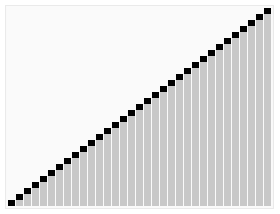
الفكرة الرئيسية
يقسم Quicksort أولاً صفيفًا كبيرًا إلى اثنين من العوامل الفرعية الأصغر: العناصر المنخفضة والعناصر العالية بالنسبة لعنصر تم اختياره عشوائيًا. يمكن أن يقوم Quicksort بعد ذلك بفرز المطبوعات الفرعية بشكل متكرر. لذلك ، فإن النقطة الرئيسية في الفرز السريع هي اختيار عنصر التقسيم.
ملكيات
Back to Top
الفكرة الرئيسية
من خلال تكرار أوقات خوارزمية الانكماش مع خيارات عشوائية مستقلة وإعادة أصغر قطع ، فإن احتمال عدم العثور على الحد الأدنى
ملكيات
Back to Topوضع هياكل البيانات كقسم مستقل مضلل ؛ ومع ذلك ، سأقدم مشاكل محيرة يتم حلها بأناقة بواسطة هياكل البيانات. قد يكون لبعض هياكل البيانات استراتيجية تصميم الخوارزمية لم تتم مراجعتها بعد.
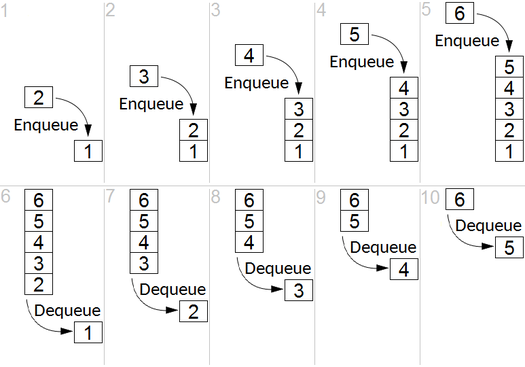
الفكرة الرئيسية
يستخدم BFS لحساب العقد القابلة للوصول من عقدة مصدر في رسم بياني غير موجه أو موجه. تتم طباعة العقد القابلة للوصول بالترتيب الموجود. يتم استخدام قائمة انتظار لتخزين العقد الرمادية الملونة (انظر GIF أدناه). مصطلح "اتساع" في BFS يعني إيجاد عقدة يمكن الوصول إليها مع أقصر طول. يمتد اتساع الحدود بين العقد التي تمت زيارتها والعقد غير المكتشفة.
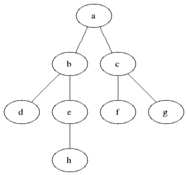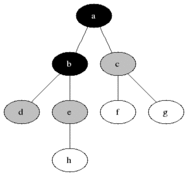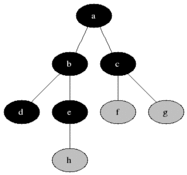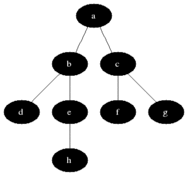
ملكيات
Back to Top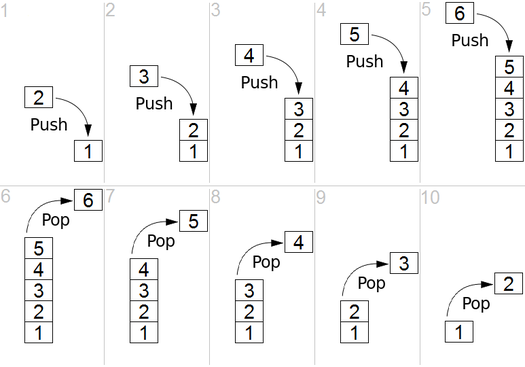
الفكرة الرئيسية
ويستخدم DFS في الرسم البياني الموجه ويخبر عدد العقد التي يمكن أن تصل إليها عقدة المصدر وطباعتها بالترتيب الذي نجده. نستخدم المكدس لتخزين العقد التي نصنفها كنقاط البداية للرسم البياني. "العمق" في اسمه يعني أن هذه الخوارزمية ستذهب بعمق قدر الإمكان بالنسبة لمصدر معين وعندما تصل إلى نقطة النهاية ، فإنها تعود إلى عقدة البداية.
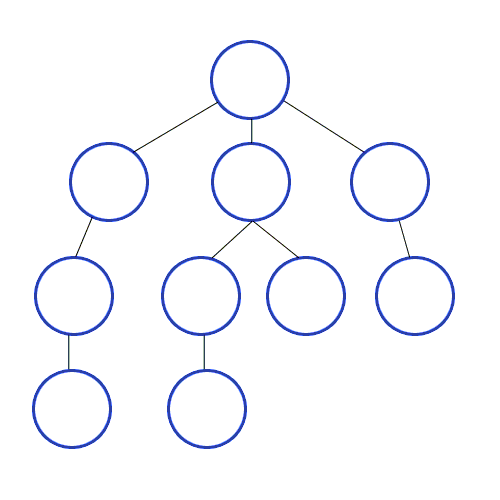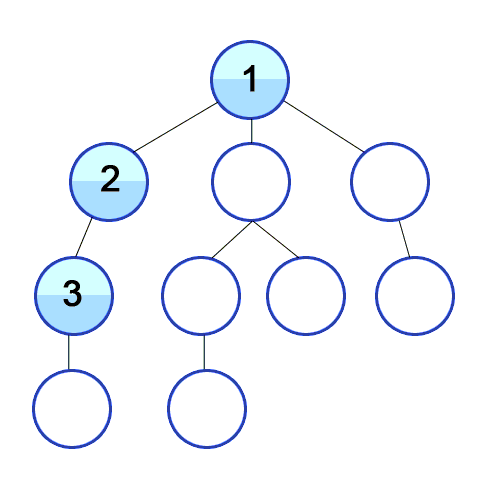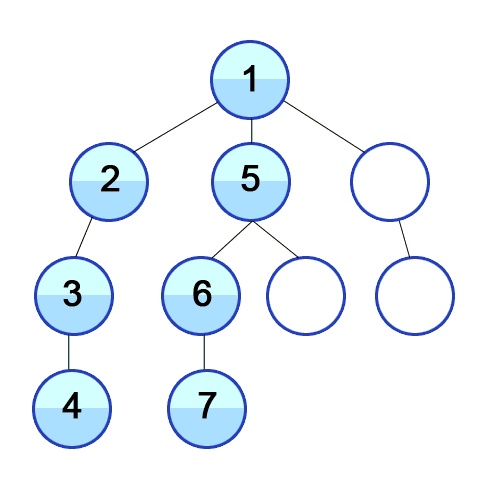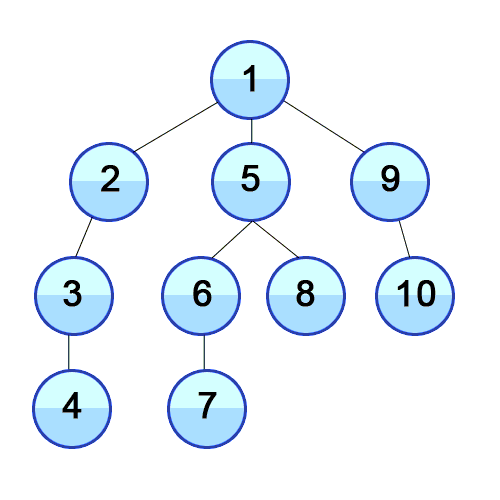
ملكيات
Back to Top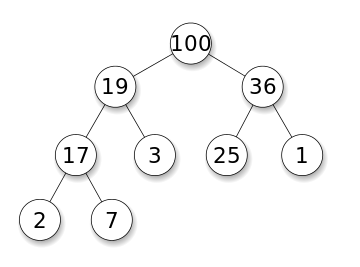
مشكلة الصيانة المتوسطة هي أنه إذا تتم قراءة الأعداد الصحيحة من دفق البيانات ، فابحث عن متوسط العناصر التي تقرأها ذلك بطريقة فعالة. للبساطة افترض أنه لا توجد تكرارات.
الفكرة الرئيسية
يمكننا استخدام كومة أقصى على الجانب الأيسر لتمثيل العناصر التي تكون أقل من الوسيط فعال ، وكومة دقيقة على الجانب الأيمن لتمثيل العناصر التي تكون أكبر من الوسيط الفعال. عندما يكون الفرق بين حجم أكوامين أكبر أو يساوي 2 ، فإننا نقوم بتبديل عنصر إلى كومة أخرى أصغر حجمًا.
ملكيات
Back to Top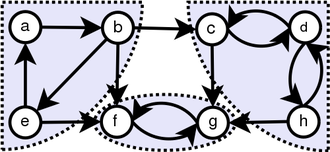
الفكرة الرئيسية
من خلال الملاحظة البسيطة ، اكتشفنا أن Tranpose of Graph لديه نفس SCCs مثل الرسم البياني الأصلي. ندير DFS مرتين. لأول مرة ، نقوم بتشغيله على G وحساب وقت التشطيب لكل قمة. وبعد ذلك ، نقوم بتشغيل DFS على g^t ولكن في الحلقة الرئيسية من DFS ، فكر في الرؤوس من أجل انخفاض وقت التشطيب.
ملكيات
Back to Top
الفكرة الرئيسية
في رسم بياني غير موجه ، يمكننا استخدام بنية البيانات هذه لمعرفة عدد SCCs. يوضح الشكل أدناه كيف يعمل.
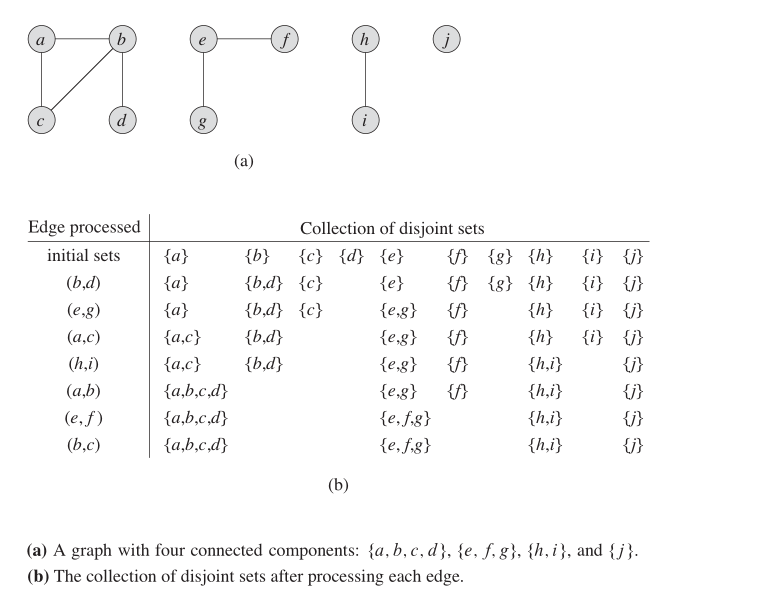
ملكيات
Back to Top في هذا القسم ، سأقدم خوارزميات الجشع ، استراتيجية تصميم خوارزمية قوية واحدة.
من Wikipedia ، تعد الخوارزمية الجشع نموذجًا خوارزميًا يتبع حل المشكلات في اتخاذ القرار الأمثل محليًا في كل مرحلة [1] على أمل إيجاد عالمي الأمثل. في العديد من المشكلات ، لا تنتج استراتيجية الجشع بشكل عام حلًا مثاليًا ، ولكن مع ذلك قد يؤدي الاستدلال الجشع إلى حلول مثالية محليًا تقرب الحل الأمثل العالمي في وقت معقول.
في مشكلة اختيار النشاط ، كل نشاط له وزنه وطوله. وهدفنا هو تقليل مجموع الوزن*. إنه مثال سهل للغاية ورائع لإظهار كيف تعمل الخوارزمية الجشع وتقديم دليل أنيق باستخدام تقنية تبادل الحجة.
الفكرة الرئيسية
إذا قمنا بفرز النشاط حسب قيمة الوزن/الطول ، فيمكننا إثبات أن الهيكل الأمثل الحالي لا يمكن أن يكون أفضل من هذا الترتيب. 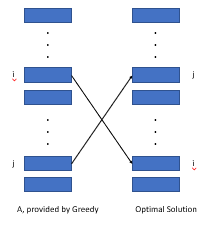
كما هو موضح أعلاه ، فإننا نعتبر التكلفة الناجمة عن نشاطين تراوحت بشكل مختلف في ترتيبين (I ، J). اكتشفنا أن التكلفة في الخوارزمية الجشع أصغر من الهيكل الأمثل من خلال قيمة wi*lj - wj*li ، والتي هي أكبر من أو تساوي 0.
ملكيات
Back to Top
الفكرة الرئيسية
قمنا بفرز المصفوفة وفقًا لوقت النهاية. وضعت الخوارزمية أول وظيفة لها وقت بدء أكبر من وقت الانتهاء من الوظيفة الأخيرة.
ملكيات
Back to Top
طريقة واحدة لترميز هذا الكتاب هي استخدام ترميز الطول الثابت. كما هو موضح أدناه:
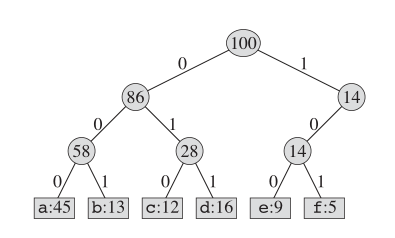
أما بالنسبة لترميز هوفمان ، فإن بنية الأشجار الفعلية تبدو مثل هذا:
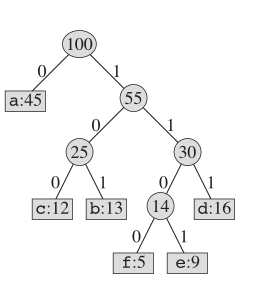
الفكرة الرئيسية
نحافظ على شجرة ثنائية وننشئ عقدة جديدة كوالد لروحين أقل مرونة. والمفتاح لهذه العقدة الجديدة هو مجموع مفاتيح طفليها. نكرر هذا حتى لا توجد عقد في هذا "الكتاب".
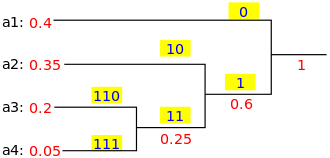
ملكيات
Back to Topخوارزمية Dijkstra هي خوارزمية للعثور على أقصر المسارات بين العقد في الرسم البياني. ومع ذلك ، فإنه يحتوي على شرط واحد ، يجب أن تكون جميع المسارات أكبر أو تساوي 0.
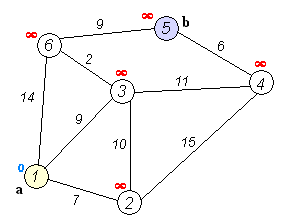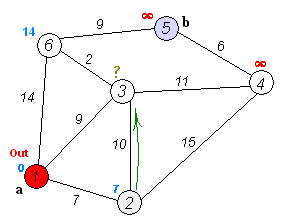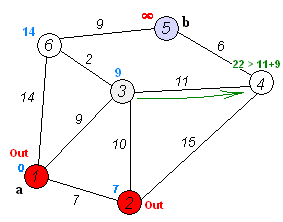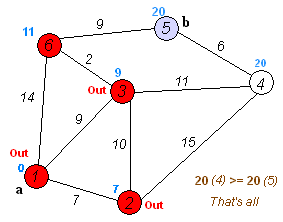
الفكرة الرئيسية
منفصلة العقد في مجموعتين ، يتم وضع علامة على مجموعة واحدة كما تم استكشافها. ونقوم بتحديث المسافة من المجموعة غير المستكشفة إلى المجموعة التي تم استكشافها بأقصر مسافة.
ملكيات
Back to Top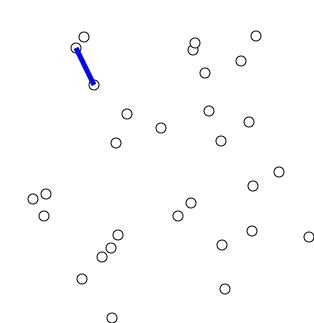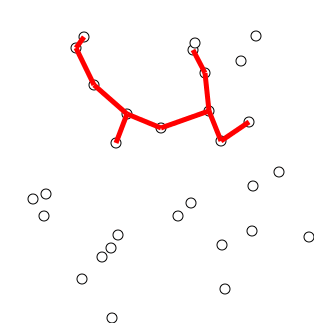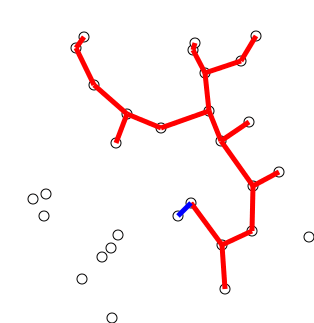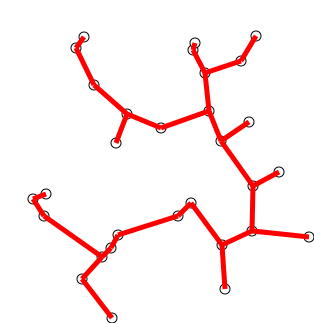
الفكرة الرئيسية
يمكن وصف الخوارزمية بشكل غير رسمي بأنها تنفيذ الخطوات التالية:
تهيئة شجرة بقمة واحدة ، تم اختيارها بشكل تعسفي من الرسم البياني.
قم بزراعة الشجرة بحافة واحدة: من الحواف التي تربط الشجرة بالقسمة التي لم تصل إلى الشجرة بعد ، وابحث عن حافة الوزن الدنيا ، وقم بنقلها إلى الشجرة.
كرر الخطوة 2 (حتى تكون جميع القمم في الشجرة).
ملكيات
Back to Top
الفكرة الرئيسية
يشبه إلى حد كبير SCC ، يمكننا إيقاف Alogrithm في وقت مبكر للتحكم في عدد الفصول في الرسم البياني الخاص بنا ، وهذا يعني أنه يمكننا تجميع الرسم البياني.
ملكيات
Back to Top في هذا القسم ، سأقدم خوارزميات ديناميكية ، استراتيجية تصميم خوارزمية قوية واحدة.
من Wikipedia ، تعد البرمجة الديناميكية (المعروفة أيضًا باسم التحسين الديناميكي) طريقة لحل مشكلة معقدة عن طريق تقسيمها إلى مجموعة من المشكلات الفرعية البسيطة ، وحل كل من هذه المشكلات الفرعية مرة واحدة فقط ، وتخزين حلولها.
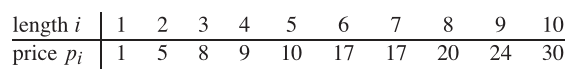
لذلك ، إذا كان طول القضيب هو 8 وقيم القطع المختلفة على النحو التالي ، فإن القيمة القصوى التي يمكن الحصول عليها هي 22 (عن طريق قطع قطعتين من الطويتين 2 و 6).
الفكرة الرئيسية
ننظر إلى التحلل الذي يتكون من قطعة أولى من الطول ، لقد قطعت الطرف الأيسر ، ثم بقية اليد اليمنى من الطول n-i. لذلك ، يشبه الرمز الكاذب:
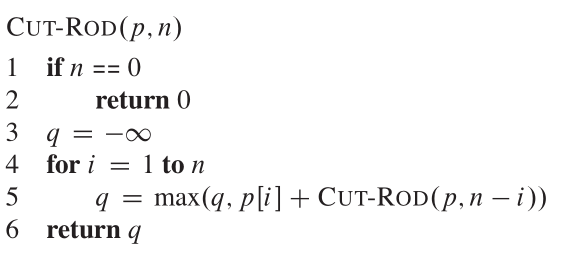
تبدو شجرة العودية التي تظهر المكالمات العودية الناتجة عن مكالمة cut_rod (p ، n):
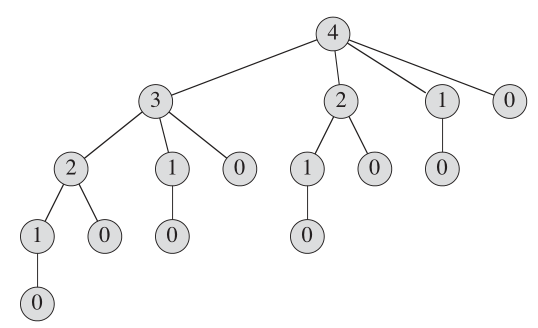
من أجل حفظ الحساب المتكرر للمشاكل الفرعية الصغيرة ، حفظنا مجموعة لتخزين هذه القيم.
ملكيات
Back to Top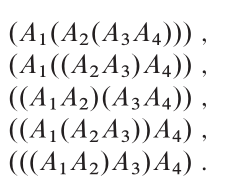
الفكرة الرئيسية
الهيكل الأمثل:
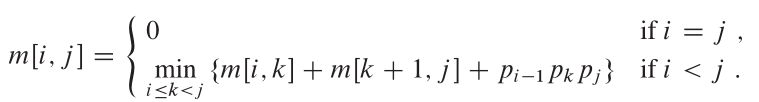
ملكيات
Back to Top الفكرة الرئيسية
من CLRs ، الهيكل الأمثل لهذه المشكلة هو:
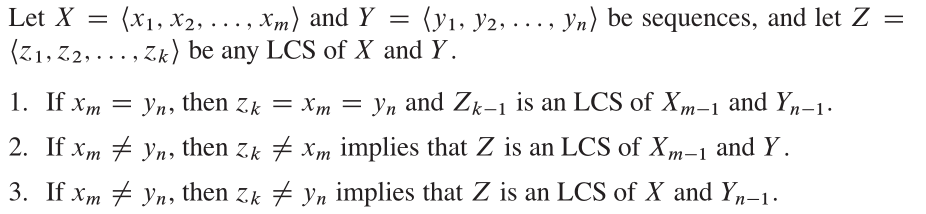
ملكيات
Back to Top الفكرة الرئيسية
تستند هذه الخوارزمية إلى ملاحظة بديهية للغاية. لنفترض أن لدينا مجموعة فرعية {1 ، 2 ، 3 ، 4 ، ... ، k} (تشير إلى V (k)) لمجموعة القمم الأصلية {1 ، 2 ، 3 ، ... ، n}. إذا كان P هو أقصر مسار من I إلى J في V (K) ، فلدينا حالتان. أولاً ، إذا لم يكن K في P ، فيجب أن يكون P مسارًا أقصر في V (K-1). ثانياً ، إذا كان K في P ، فيمكننا فصل المسار إلى قسمين ، P1: i K ، P2: K. ي. ويجب أن يكون P1 أقصر مسار من I إلى K مع V (K-1) ، يجب أن يكون P2 هو أقصر مسار من K إلى J مع V (K-1).
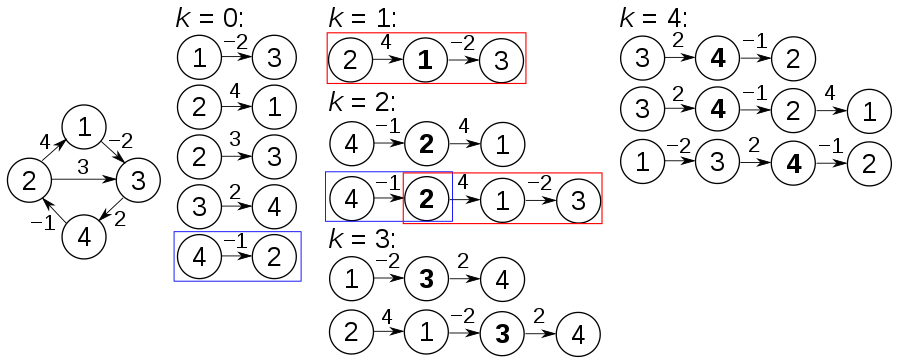
ملكيات
Back to Top من ويكيبيديا ، فإن مشكلة القرار المكتملة NP هي مشكلة تابعة لكل من فئات التعقيد NP و NP-Hard. في هذا السياق ، تعني NP "وقت متعدد الحدود غير المحدود". غالبًا ما يتم الإشارة إلى مجموعة المشكلات NP-Complete بواسطة NP-C أو NPC.
في هذا القسم ، سأقدم ثلاث مشاكل شهيرة في NPC وشرح خوارزميات التقريب للتعامل معها.
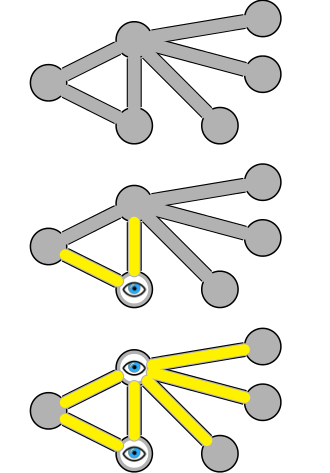
الفكرة الرئيسية
من الصعب للغاية العثور على غطاء قمة الحد الأدنى ، لكن يمكننا العثور على غطاء تقريبي مع مرتين على الأكثر في وقت متعدد الحدود.

ملكيات
Back to Top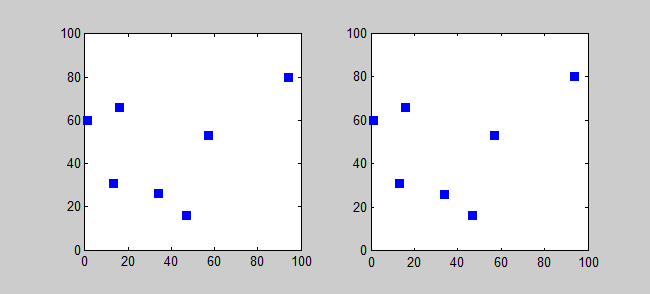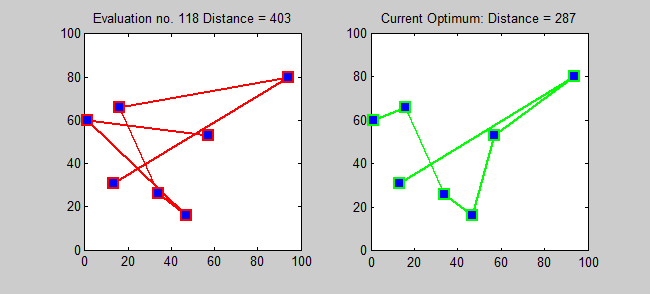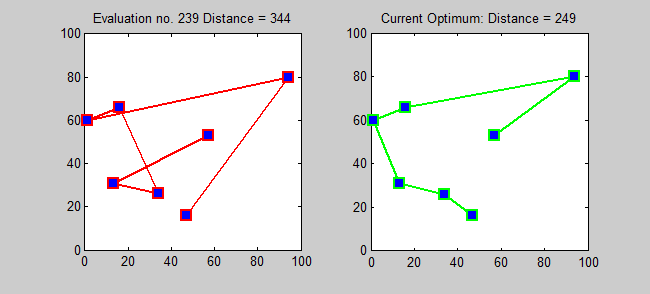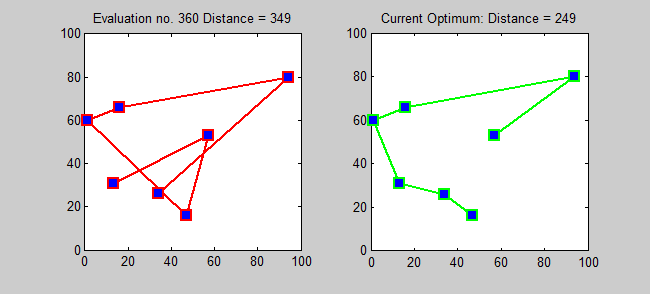
الفكرة الرئيسية
خوارزمية التقريب لـ TSP هي خوارزمية جشع (CLRS P1114). هنا ، أريد أيضًا تقديم خوارزمية دقيقة لـ TSP باستخدام البرمجة الديناميكية.
subproblem: لكل وجهة j ∈ {1،2 ، ... ، n} ، كل مجموعة فرعية S ⊆ {1،2 ، ... ، n} التي تحتوي على 1 و j ، اسمح LS ، J = الحد الأدنى للمسار من 1 إلى J الذي يزور بالضبط رؤوس S [بالضبط مرة واحدة]. لذلك ، تكرار المقابل:
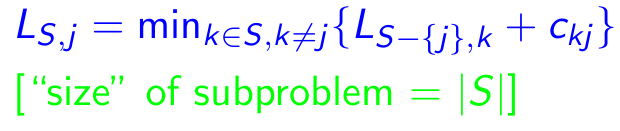
ملكيات
Back to Top 3-SAT هي واحدة من مشكلات KARP 21 NP-COMPLETE ، ويستخدم كنقطة انطلاق لإثبات أن المشكلات الأخرى هي أيضًا NP-HARD.
هنا ، أقدم خوارزمية باباديميتريو من أجل 2-سات (هذه خوارزمية مثيرة للغاية للغاية ، لذلك قررت تقديمها على الرغم من أن 2-SAT ليست NPC).
الفكرة الرئيسية
اختر تعيينًا أوليًا عشوائيًا واختر شرط غير راضٍ تعسفي وقلب قيمة أحد متغيره. هنا هو الرمز الكاذب:

مثل هذا التعامل غير الرسمي مع البنود من شأنه أن يعطينا احتمالًا كبيرًا للغاية للعثور على الإجابة الحقيقية. تكمن الآلية في مصطلح الفيزياء (المشي العشوائي). إذا كنت مهتمًا ، فإنني أوصيك بشدة بالمرور على مدى رفقاء المشي العشوائي إلى Papadimitriou.
ملكيات
Back to Top