这个存储库,我将使用Python实施一些著名的算法。该算法是根据所使用的策略排列的。每种算法将对它试图解决的问题和一些相关资源都有解释。
(该存储库的目的是为我所回顾的所有这些出色的算法创建一个美丽的读数。)
内容:
本节,我将讨论著名的鸿沟和征服策略,并展示此策略的某些应用。
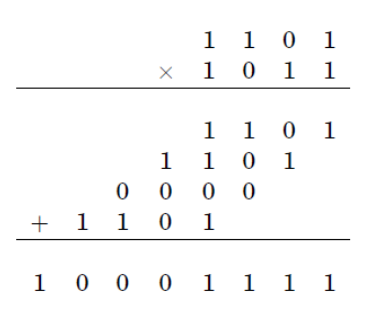
乘以两个N数字的标准过程需要与成正比的许多基本操作。至于Karatsuba算法,它最多减少了运行时间
关键主意
Karatsuba算法的基本步骤是一个公式,该公式允许一个公式计算两个大数字的乘积,并使用三个较小数字的乘法,每个数字的数字大约是或数字的一半,以及一些添加和数字偏移。
特性
Back to Top
该算法最糟糕的运行时间是。
上面的GIF显示合并排序的工作方式: 
关键主意
将未分类的列表分为n个sublist,每个列表包含1个元素(1个元素的列表被认为是分类的),然后反复合并订书片以产生新的排序订阅者,直到只剩下1个sublist。这将是排序列表。
特性
Back to Top
关键主意
像上图一样,当我们在合并操作中首次从右子阵列中接收元素时,这表明右元素小于(左子阵列的长度 - 左元素的索引)元素。
随着算法的进行,添加所有反转将为我们提供总倒置。
特性
Back to Top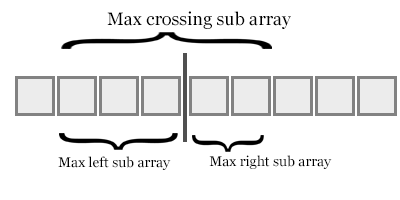
特性
Back to Top本节我将讨论两种算法,这些算法在内部使用了随机变量。
关键主意
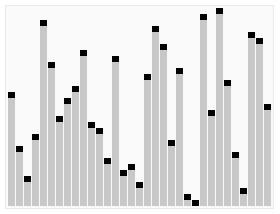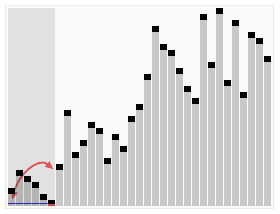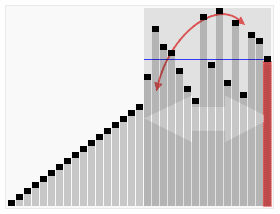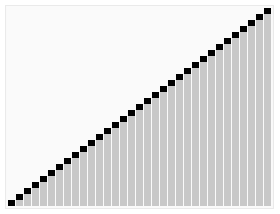
QuickSort首先将一个大阵列分为两个较小的子阵列:相对于随机选择的元素,低元素和高元素。然后,QuickSort可以递归对子阵列进行分类。因此,快速排序的关键点是选择分区元素。
特性
Back to Top
关键主意
通过独立的随机选择重复收缩算法时间并返回最小的切割,找不到最小切割的概率是
特性
Back to Top将数据结构作为独立部分具有误导性;但是,我将引入令人困惑的问题,这些问题由数据结构优雅地解决。一些数据结构可能具有尚未审查的算法设计策略。
关键主意
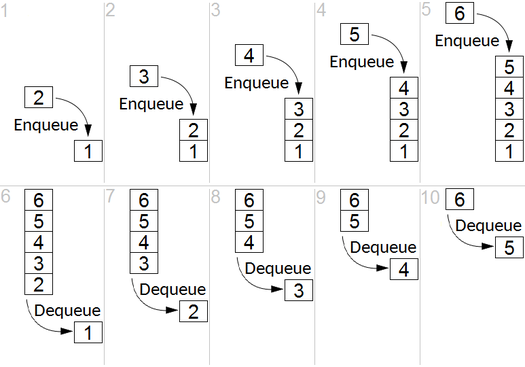
BFS用于计数从无向图或有向图中的源节点的可触发节点。可及的节点按找到的顺序打印。队列用于存储节点彩色灰色(请参见下面的GIF)。 BFS中的“广度”一词意味着找到最短长度的可触及节点。宽度延伸了访问的节点和未发现的节点之间的边界。
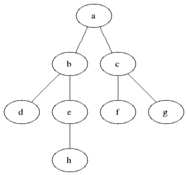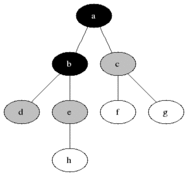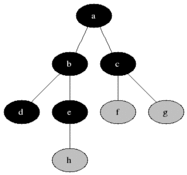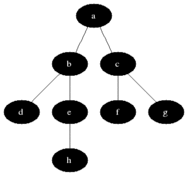
特性
Back to Top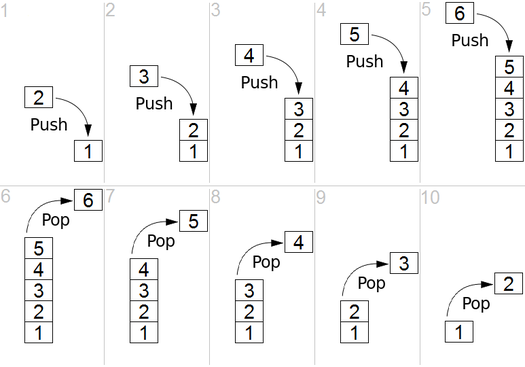
关键主意
DFS在有向图中使用,它告诉源节点可以通过我们找到的顺序打印出多少节点。我们使用堆栈存储我们将其分类为图形的开始点的节点。其名称的“深度”意味着该算法将尽可能深入地进行,当它到达端点时,它将返回到启动节点。
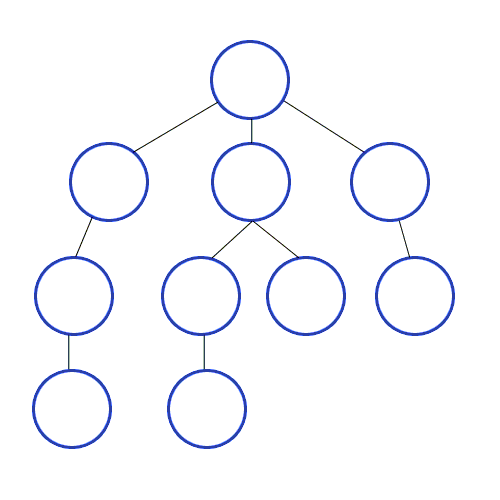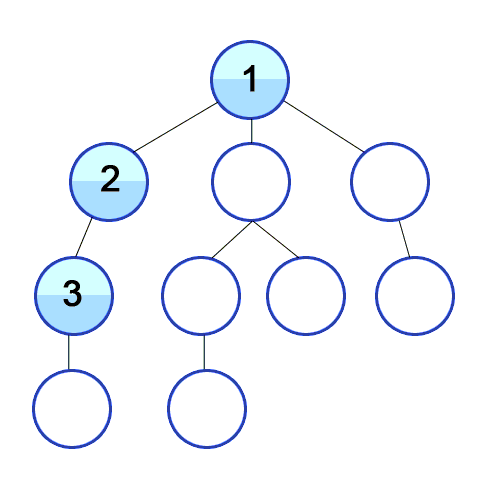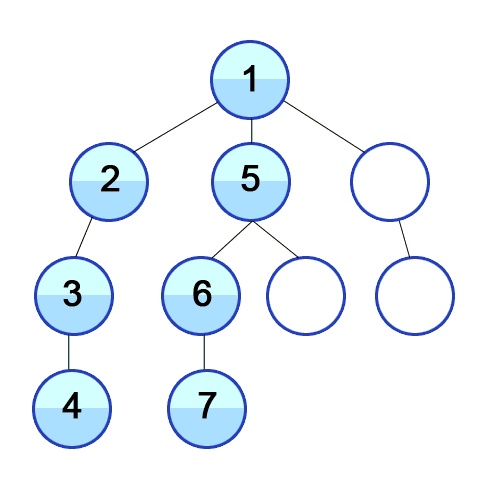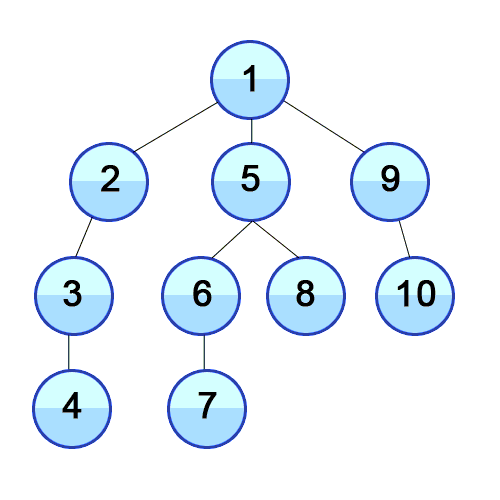
特性
Back to Top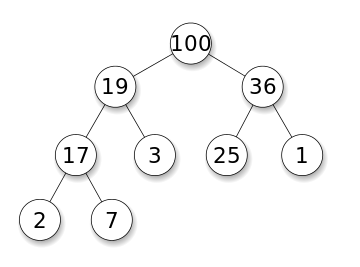
中间维护问题是,如果从数据流中读取整数,请找到有效的元素中位数。为简单起见,假设没有重复。
关键主意
我们可以在左侧使用最大堆来表示中位数不足的元素,右侧的最小堆代表了比有效中值大的元素。当两个堆的大小之间的差异更大或等于2时,我们将一个元素切换到另一个较小的尺寸堆。
特性
Back to Top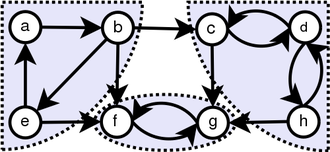
关键主意
通过简单的观察,我们发现图的tranpose具有与原始图相同的SCC。我们两次运行DFS。第一次,我们在G上运行它,并为每个顶点计算完成时间。然后,我们在g^t上运行DFS,但是在DF的主环中,以减少完成时间的顺序考虑顶点。
特性
Back to Top
关键主意
在无向图中,我们可以使用此数据结构来找出多少SCC。下图显示了其工作原理。
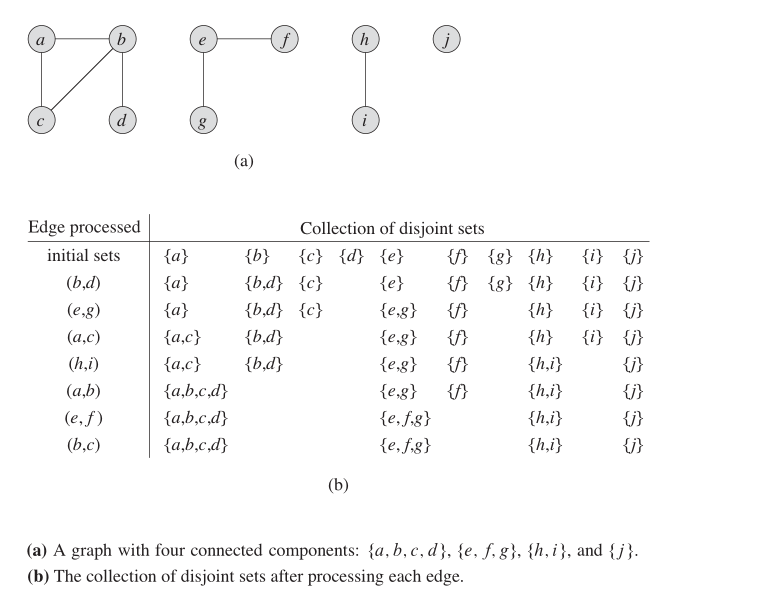
特性
Back to Top在本节中,我将介绍一种强大的算法设计策略,这是一种贪婪的算法。
从维基百科(Wikipedia),一种贪婪的算法是一种算法范式,遵循解决问题的启发式方法,即在每个阶段[1]进行本地最佳选择[1],希望能找到全球最佳选择。在许多问题中,贪婪的策略通常不会产生最佳解决方案,但是贪婪的启发式方法可能会产生本地最佳的解决方案,该解决方案在合理的时间内近似全球最佳解决方案。
在活动选择问题中,每个活动都有其自身的体重和长度。我们的目标是最大程度地减少重量*的总和。这是一个非常简单且很好的例子,可以显示贪婪算法的工作原理,并使用参数交换技术提供优雅的证明。
关键主意
如果我们按价值/长度进行分类,我们可以证明现有的最佳结构不能比这种安排更好。 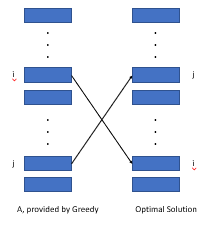
如上图所示,我们考虑了两种活动在两个安排中范围有所不同的成本(i,j)。我们发现,通过Wi*lj -wj*li的值,贪婪算法中的成本小于最佳结构,该值大于或等于0。
特性
Back to Top
关键主意
我们根据阵列的完成时间对数组进行了排序。该算法提出了第一份工作时间比上一个工作时间更大的工作。
特性
Back to Top
编码本书的一种方法是使用固定长度编码。如下所示:
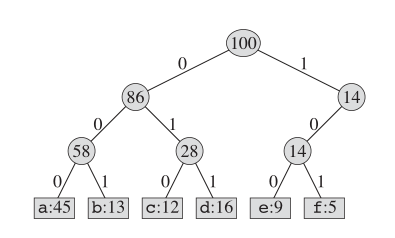
至于霍夫曼编码,实际的树结构看起来像这样:
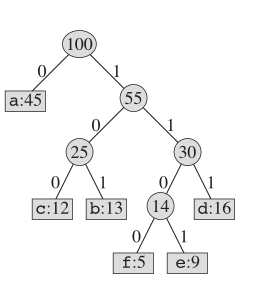
关键主意
我们维护二进制树,并创建一个新节点作为两个最小频繁的字母的父。这个新节点的关键是其两个孩子的钥匙之和。我们重复此操作,直到这本“书”中没有节点。
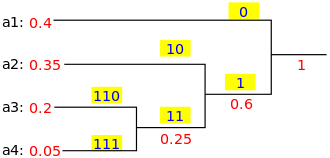
特性
Back to TopDijkstra的算法是用于查找图中节点之间最短路径的算法。但是,它具有一个先决条件,所有路径必须更大或等于0。
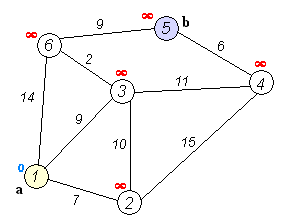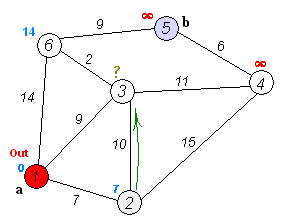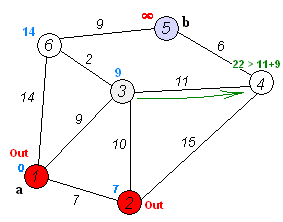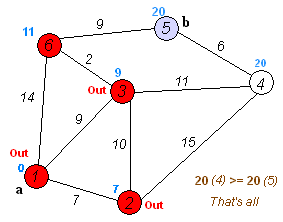
关键主意
单独的节点分为两组,一组被标记为探索。然后,我们更新了从未开发的组到探索组的距离,最短的距离。
特性
Back to Top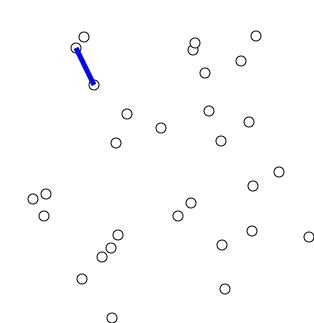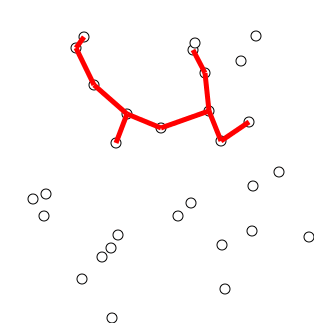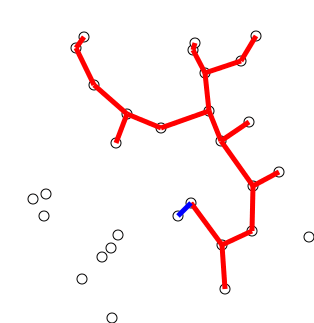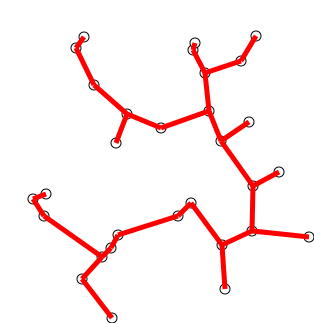
关键主意
该算法可以非正式地描述为执行以下步骤:
用单个顶点初始化树,从图形任意选择。
通过一个边来种植树:将树连接到树上尚未在树中的顶点的边缘,找到最小重量的边缘,然后将其转移到树上。
重复步骤2(直到所有顶点都在树上)。
特性
Back to Top
关键主意
与SCC非常相似,我们可以尽早停止Alogrithm来控制图中的类数,也就是说,我们可以将图形聚集。
特性
Back to Top在本节中,我将介绍动态算法,这是一种强大的算法设计策略。
从维基百科(Wikipedia)来看,动态编程(也称为动态优化)是一种通过将其分解为更简单的子问题的集合,仅求解一次这些子问题并存储解决方案来解决复杂问题。
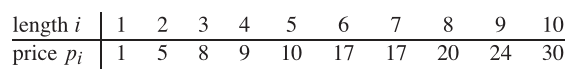
因此,如果杆的长度为8,并且给出不同零件的值如下,则最大可获得的值为22(通过切成两块长度2和6的切割)。
关键主意
我们将分解视为由第一片长度组成,我切断了左端,然后是长度为n-i的右手。因此,伪代码看起来像:
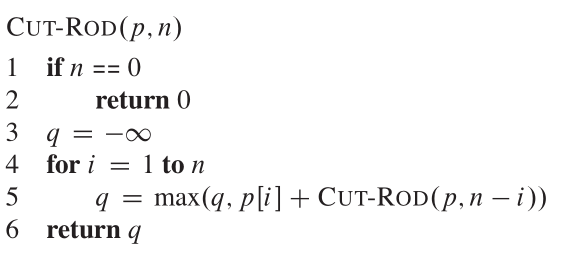
递归树显示由call cut_rod(p,n)产生的递归调用,看起来像:
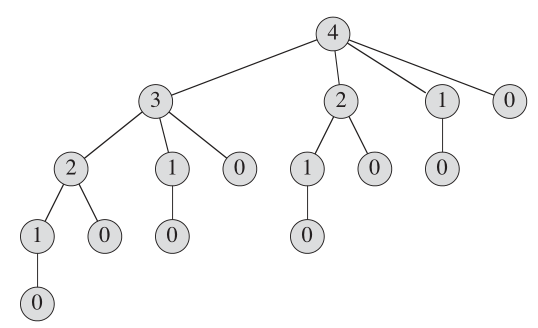
为了节省小问题的重复计算,我们记住一个数组来存储这些值。
特性
Back to Top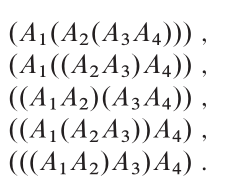
关键主意
最佳结构:
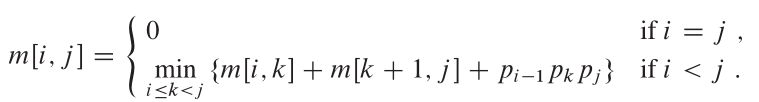
特性
Back to Top关键主意
从CLR中,此问题的最佳结构是:
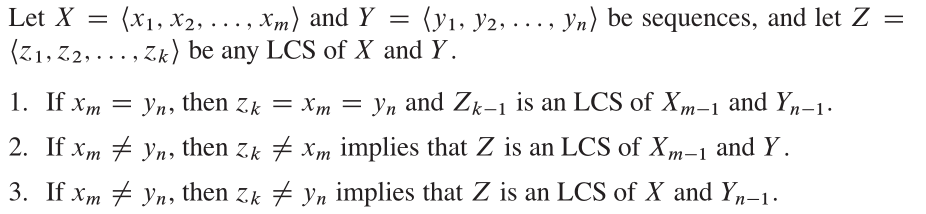
特性
Back to Top关键主意
该算法基于非常直观的观察。假设我们有一个子集{1,2,3,4,...,k}(表示为原始顶点组{1,2,3,...,n}的v(k)。如果p是从v(k)中的i到j的最短路径,我们有两种情况。首先,如果k不在p中,则p必须是v(k-1)中的最短路径。其次,如果k在p中,那么我们可以将路径分为两个,p1:i k,p2:k j。 P1必须是从i到K的最短路径(K-1),P2必须是从K到J的最短路径(K-1)。
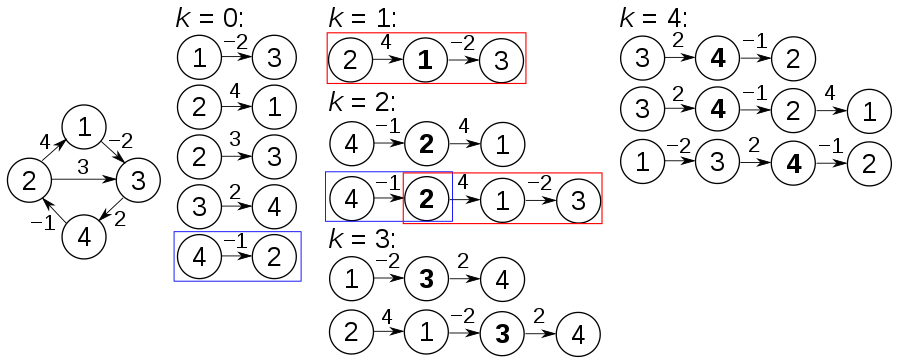
特性
Back to Top从Wikipedia来看,NP完整的决策问题既属于NP和NP-硬化的复杂性类别。在这种情况下,NP代表“非确定的多项式时间”。 NP Comperte问题集通常用NP-C或NPC表示。
在本节中,我将介绍三个非常著名的NPC问题,并解释近似算法以接近它们。
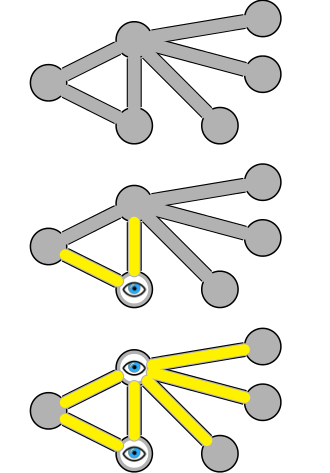
关键主意
很难找到最小顶点盖,但是我们可以在多项式时间内找到最多两倍的顶点盖。

特性
Back to Top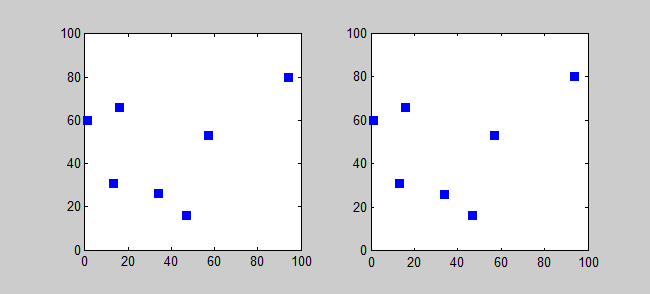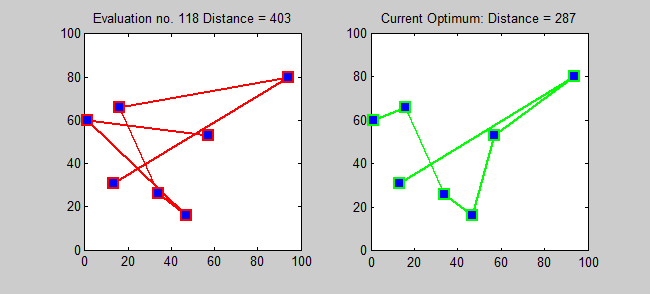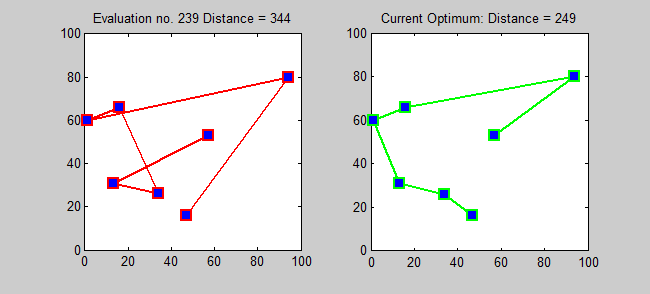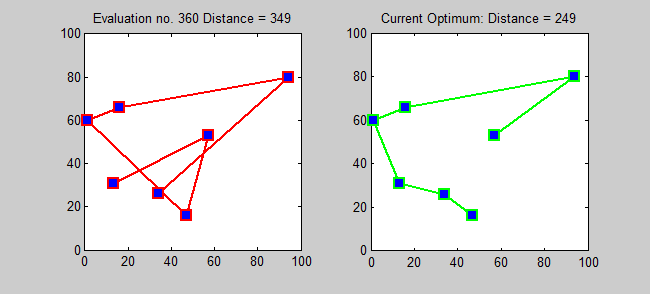
关键主意
TSP的近似算法是一种贪婪的算法(CLRS P1114)。在这里,我还想使用动态编程为TSP介绍一种精确的算法。
子问题:对于每个目标j∈{1,2,...,n},每个子集s {1,2,...,n}包含1和j,让ls,j =从1到j的路径的最小长度,从1到j,确切地访问了s的顶点[确切的每次[每次一次]]。因此,相应的复发:
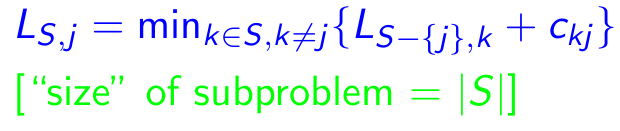
特性
Back to Top 3-SAT是KARP的21个NP完整问题之一,它被用作证明其他问题也是NP-HARD的起点。
本文中,我介绍了2个SAT的Papadimitriou算法(这是一种非常非常非常有趣的算法,因此即使2-SAT不是NPC,我也决定将其介绍。
关键主意
选择随机的初始分配,然后选择任意不满意的子句,然后翻转其变量之一的值。这是伪代码:

这样的随意处理条款将使我们有很大的可能性找到真正的答案。该机制在于物理学术语(随机步行)。如果您有兴趣,我强烈建议您进行随机步行与Papadimitriou的关系。
特性
Back to Top