Ce référentiel, j'utiliserai Python pour implémenter des algorithmes célèbres. Les algorithmes sont organisés en fonction de la stratégie utilisée. Chaque algorithme aura une explication du problème qu'il tente de résoudre et de certaines ressources pertinentes.
(Le but de ce référentiel est de créer une belle lecture pour tous ces algorithmes brillants que j'ai examinés.)
Contenu:
Cette section, je parlerai de la célèbre stratégie de division et de conquérant et montrerai quelques applications de cette stratégie.
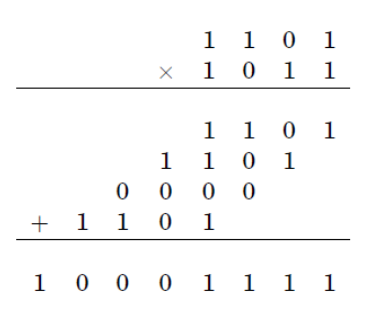
La procédure standard de multiplication de deux nombres à n chiffres nécessite un certain nombre d'opérations élémentaires proportionnelles à. Quant à l'algorithme de Karatsuba, il réduit le temps de fonctionnement au plus
Idée clé
L'étape de base de l'algorithme de Karatsuba est une formule qui permet de calculer le produit de deux grands nombres et d'utiliser trois multiplications de nombres plus petits, chacun avec environ la moitié autant de chiffres que ou, plus certains ajouts et changements de chiffres.
Propriétés
Back to Top
Le pire temps de fonctionnement pour cet algorithme est.
GIF ci-dessus montre comment la fusion fonctionne: 
Idée clé
Divisez la liste non triée en n sublilistes, chacun contenant 1 élément (une liste de 1 élément est considérée comme triée) et fusionnent à plusieurs reprises des sous-listes pour produire de nouveaux sublilistes triés jusqu'à ce qu'il ne reste que 1 subliste. Ce sera la liste triée.
Propriétés
Back to Top
Idée clé
Comme la figure ci-dessus, lorsque nous prenons l'élément pour la première fois de la sous-table droite en fonctionnement de la fusion, qui indique que l'élément droit est plus petit que (longueur de la sous-tableau gauche - l'indice de l'élément gauche).
Au fur et à mesure que l'algorithme progresse, ajouter toutes les inversions nous donneront les inversions totales.
Propriétés
Back to Top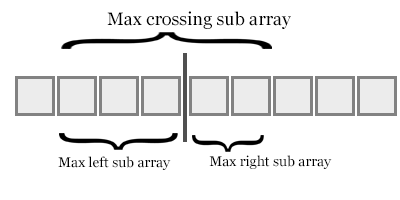
Propriétés
Back to TopCette section, je parlerai de deux algorithmes qui ont utilisé une variable aléatoire à l'intérieur.
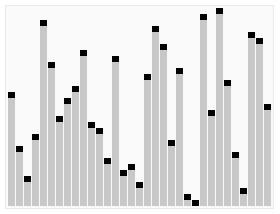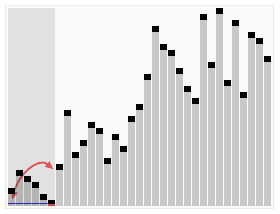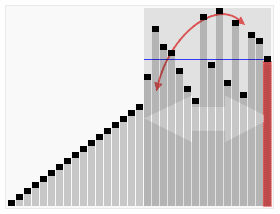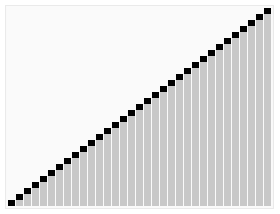
Idée clé
Quicksort divise d'abord un grand tableau en deux sous-arrailles plus petites: les éléments bas et les éléments élevés par rapport à un élément choisi au hasard. Quicksort peut alors trier récursivement les sous-arraies. Ainsi, le point clé dans le tri rapide est de choisir l'élément de partition.
Propriétés
Back to Top
Idée clé
En répétant les temps d'algorithme de contraction avec des choix aléatoires indépendants et en renvoyant la plus petite coupe, la probabilité de ne pas trouver de coupe minimale est
Propriétés
Back to TopPlacer les structures de données en tant que section indépendante est trompeur; Cependant, je vais introduire des problèmes perplexes qui sont élégamment résolus par les structures de données. Certaines structures de données peuvent avoir une stratégie de conception d'algorithme qui n'a pas encore été examinée.
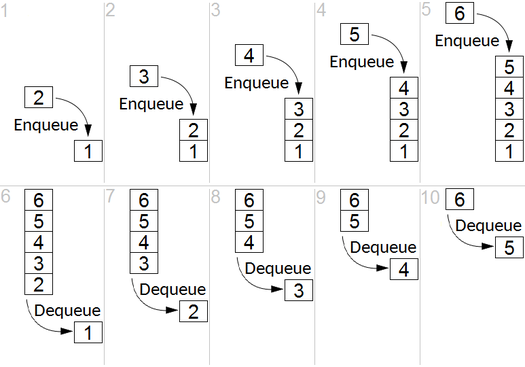
Idée clé
BFS est utilisé pour compter les nœuds accessibles à partir d'un nœud source dans un graphique non dirigé ou dirigé. Les nœuds accessibles sont imprimés dans la commande trouvée. Une file d'attente est utilisée pour stocker les nœuds de couleur gris (voir le GIF ci-dessous). Le terme «largeur» dans BFS signifie trouver un nœud accessible avec la plus courte longueur. La largeur étend la frontière entre les nœuds visités et les nœuds non découverts.
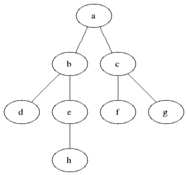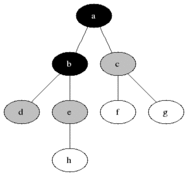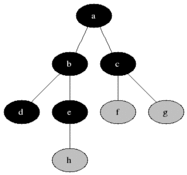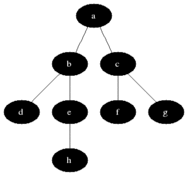
Propriétés
Back to Top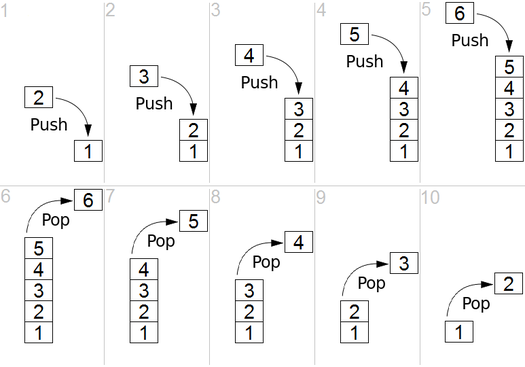
Idée clé
Et DFS est utilisé dans le graphique dirigé et il indique combien de nœuds un nœud source peut les atteindre et les imprimer par l'ordre que nous les trouvons. Nous utilisons la pile pour stocker les nœuds que nous classons comme les points de départ du graphique. La "profondeur" en son nom signifie que cet algorithme ira aussi profondément que possible pour une source donnée et lorsqu'il atteindra le point de terminaison, il revient au nœud de démarrage.
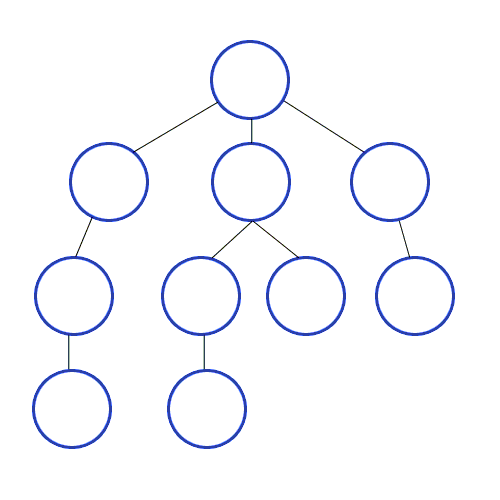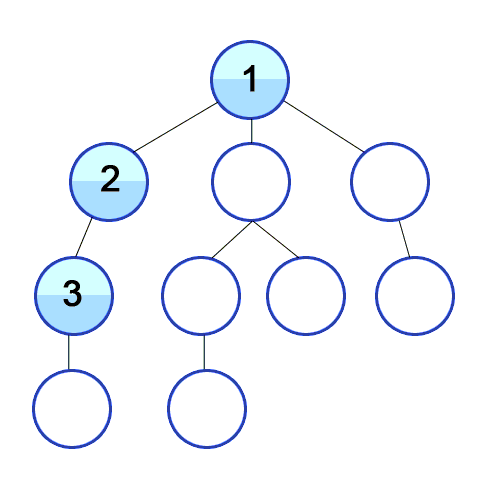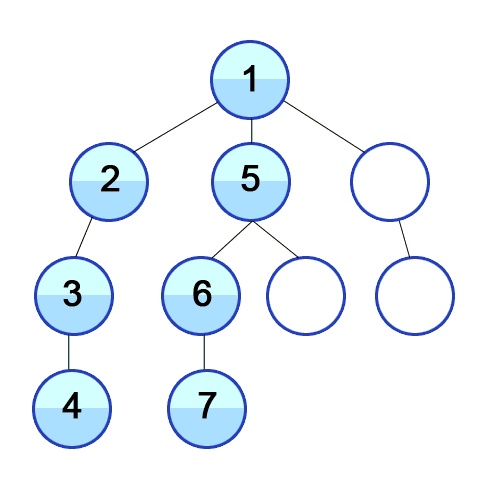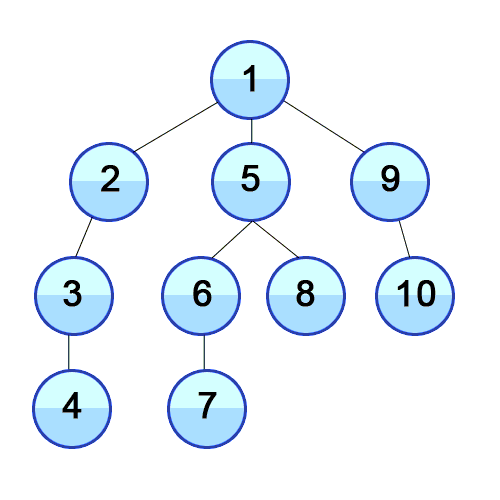
Propriétés
Back to Top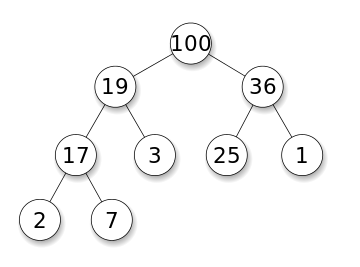
Le problème de maintenance médian est que si les entiers sont lus à partir d'un flux de données, trouvez la médiane d'éléments le lire de manière efficace. Pour simplifier, supposons qu'il n'y a pas de doublons.
Idée clé
Nous pouvons utiliser un tas maximal sur le côté gauche pour représenter des éléments qui sont moins que la médiane efficace, et un tas min sur le côté droit pour représenter des éléments supérieurs à la médiane efficace. Lorsque la différence entre la taille de deux tas est supérieure ou égale à 2, nous passons un élément à un autre tas de taille plus petite.
Propriétés
Back to Top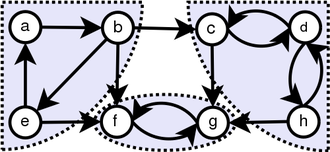
Idée clé
Grâce à une observation simple, nous découvrons que Tranpose of Graph a les mêmes SCC que le graphique d'origine. Nous exécutons DFS deux fois. Première fois, nous l'exécutons sur G et calculons l'heure de finition pour chaque sommet. Et puis, nous exécutons des DF sur g ^ t mais dans la boucle principale de DFS, considérons les sommets dans l'ordre de diminuer le temps de finition.
Propriétés
Back to Top
Idée clé
Dans un graphique non dirigé, nous pouvons utiliser cette structure de données pour savoir combien de SCC. La figure ci-dessous montre comment elle fonctionne.
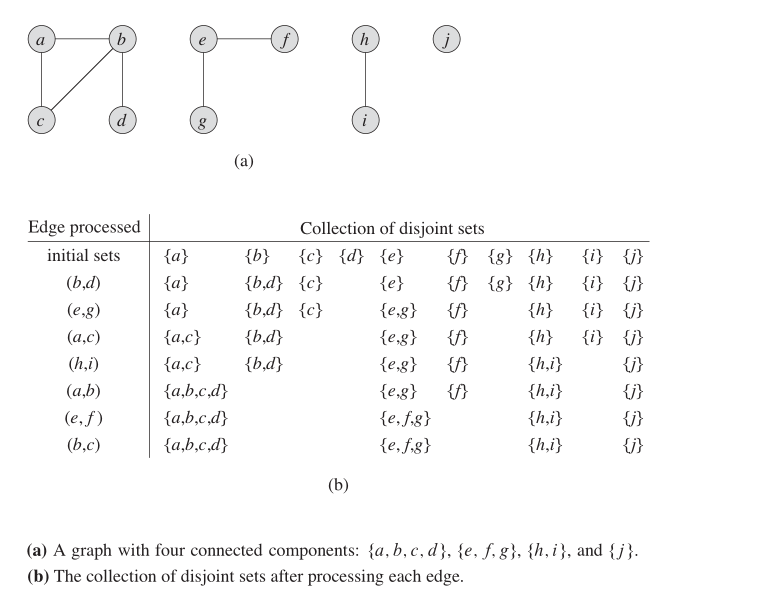
Propriétés
Back to Top Dans cette section, je vais présenter des algorithmes gourmands, une puissante stratégie de conception d'algorithmes.
De Wikipedia, un algorithme gourmand est un paradigme algorithmique qui suit l'heuristique de résolution de problèmes de faire le choix localement optimal à chaque étape [1] dans l'espoir de trouver un optimum mondial. Dans de nombreux problèmes, une stratégie gourmand ne produit pas en général une solution optimale, mais néanmoins une heuristique gourmand peut donner des solutions optimales localement qui approximativement une solution optimale globale dans un temps raisonnable.
Dans le problème de la sélection des activités, chaque activité a son propre poids et longueur. Et notre objectif est de minimiser la somme de la longueur du poids *. C'est un exemple très facile et excellent pour montrer comment l'algorithme gourmand fonctionne et fournir une preuve élégante en utilisant la technique d'échange d'argument.
Idée clé
Si nous trions l'activité par poids / longueur de valeur, nous pouvons prouver qu'une structure optimale existante ne peut pas être meilleure que cet arrangement. 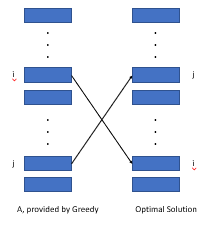
Comme la figure indiquée ci-dessus, nous considérons le coût causé par deux activités qui sont variées différemment dans deux arrangements (i, j). Nous découvrons que le coût dans l'algorithme gourmand est inférieur à la structure optimale par la valeur de wi * lj - wj * li, qui est supérieure ou égale à 0.
Propriétés
Back to Top
Idée clé
Nous avons trié le tableau en fonction de son temps d'arrivée. L'algorithme a mis le premier emploi dont l'heure de début est plus grande que l'heure d'arrivée du dernier emploi.
Propriétés
Back to Top
Une façon d'encoder ce livre est d'utiliser le codage fixe de longueur. Comme indiqué ci-dessous:
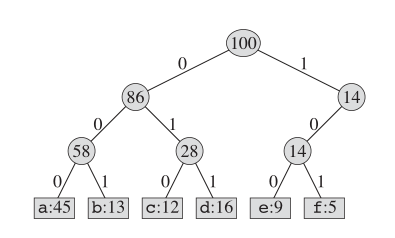
Quant au codage de Huffman, la structure réelle de l'arbre ressemble à ceci:
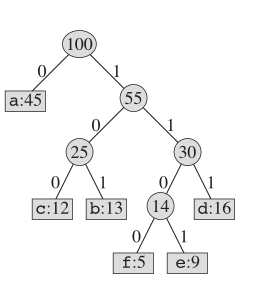
Idée clé
Nous maintenons un arbre binaire et créons un nouveau nœud en tant que parent pour deux lettres les moins fréquentes. Et la clé de ce nouveau nœud est la somme des clés de ses deux enfants. Nous répétons cela jusqu'à ce qu'il ne reste plus de nœuds dans ce "livre".
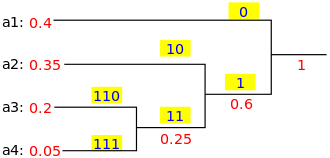
Propriétés
Back to TopL'algorithme de Dijkstra est un algorithme pour trouver les chemins les plus courts entre les nœuds d'un graphique. Cependant, il a une condition préalable, tous les chemins doivent être supérieurs ou égaux à 0.
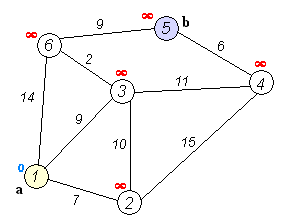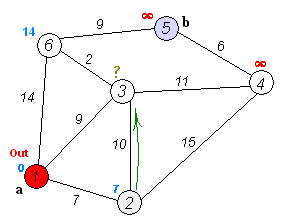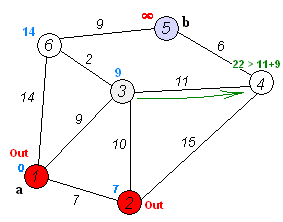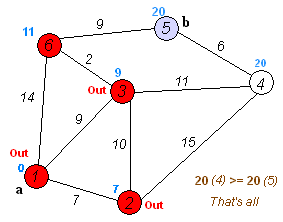
Idée clé
Séparer les nœuds en deux groupes, un groupe est marqué comme exploré. Et nous mettons à jour la distance du groupe inexploré à un groupe exploré par la distance la plus courte.
Propriétés
Back to Top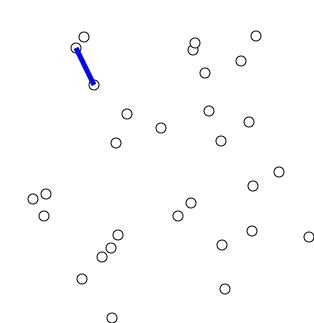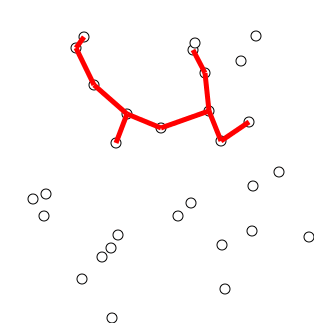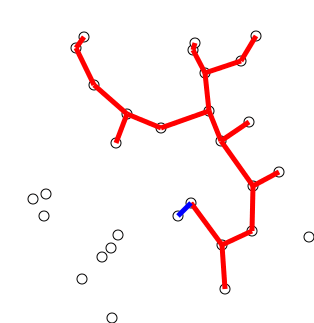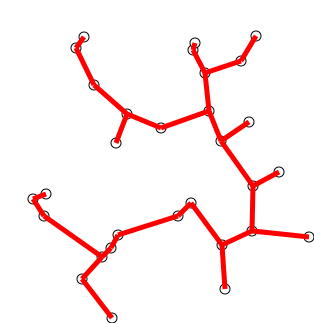
Idée clé
L'algorithme peut être décrit de manière informelle comme effectuant les étapes suivantes:
Initialisez un arbre avec un seul sommet, choisi arbitrairement à partir du graphique.
Faites pousser l'arbre par un bord: des bords qui relient l'arbre aux sommets non encore dans l'arbre, trouvez le bord minimum et transférez-le à l'arbre.
Répétez l'étape 2 (jusqu'à ce que tous les sommets soient dans l'arbre).
Propriétés
Back to Top
Idée clé
Très similaire à SCC, nous pouvons tôt arrêter l'alogrithme pour contrôler le nombre de classes dans notre graphique, c'est-à-dire que nous pouvons regrouper le graphique.
Propriétés
Back to Top Dans cette section, je vais introduire des algorithmes dynamiques, une puissante stratégie de conception d'algorithmes.
De Wikipedia, la programmation dynamique (également connue sous le nom d'optimisation dynamique) est une méthode pour résoudre un problème complexe en le décomposant en une collection de sous-problèmes plus simples, en résolvant chacun de ces sous-problèmes une seule fois et en stockant leurs solutions.
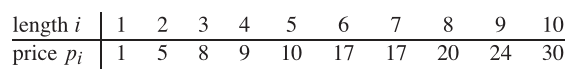
Ainsi, si la longueur de la tige est de 8 et que les valeurs de différentes pièces sont données comme suivantes, la valeur maximale obtenue est de 22 (en coupant en deux morceaux de longueurs 2 et 6).
Idée clé
Nous considérons une décomposition comme composée d'un premier morceau de longueur que j'ai coupé l'extrémité gauche, puis un reste de la longueur à droite n - i. Donc, le pseudocode ressemble:
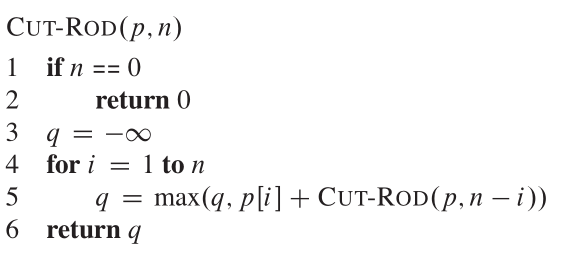
L'arbre de récursivité montrant des appels récursifs résultant d'un appel Cut_rod (p, n) ressemble:
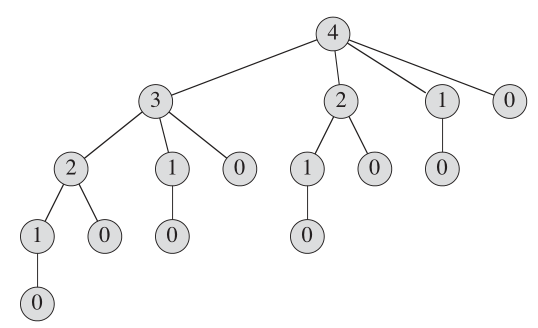
Afin de sauvegarder le calcul répété pour les petits sous-problèmes, nous avons mémorisé un tableau pour stocker ces valeurs.
Propriétés
Back to Top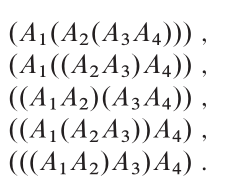
Idée clé
Structure optimale:
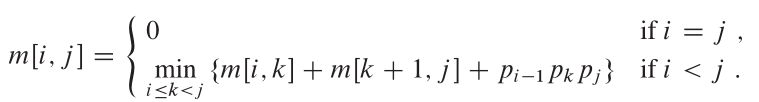
Propriétés
Back to Top Idée clé
De CLRS, la structure optimale de ce problème est:
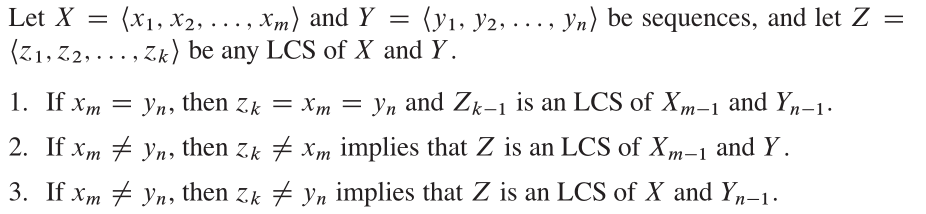
Propriétés
Back to Top Idée clé
Cet algorithme est basé sur une observation très intuitive. Supposons que nous ayons un sous-ensemble {1, 2, 3, 4, ..., k} (désigne V (k)) du groupe de sommets d'origine {1, 2, 3, ..., n}. Si P est un chemin le plus court de i à j dans V (k), nous avons deux cas. D'abord, si k n'est pas en p, alors P doit être un chemin le plus court en V (K-1). Deuxièmement, si k est en p, alors nous pouvons séparer le chemin en deux, P1: I K, P2: K j. et P1 doit être le chemin le plus court de i à k avec V (K-1), P2 doit être le chemin le plus court de K à J avec V (K-1).
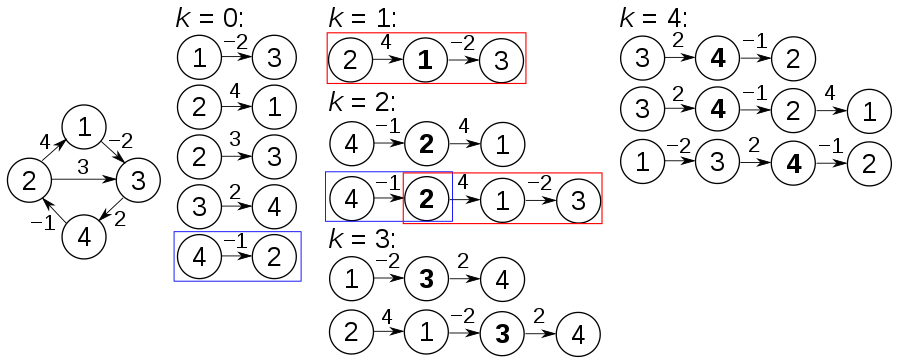
Propriétés
Back to Top De From Wikipedia, un problème de décision NP-Complete est celui appartenant à la fois au NP et aux classes de complexité NP-dur. Dans ce contexte, NP signifie «temps polynomial non déterministe». L'ensemble des problèmes NP-Complete est souvent indiqué par NP-C ou NPC.
Dans cette section, je vais présenter trois problèmes de PNJ très célèbres et expliquer les algorithmes d'approximation pour les approcher.
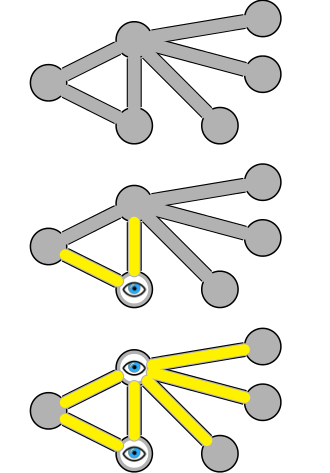
Idée clé
Il est très difficile de trouver une couverture de sommet minimum, mais nous pouvons trouver une couverture approximative avec au plus deux fois les sommets en temps polynomial.

Propriétés
Back to Top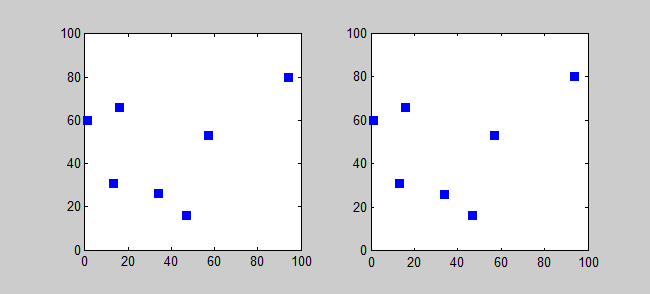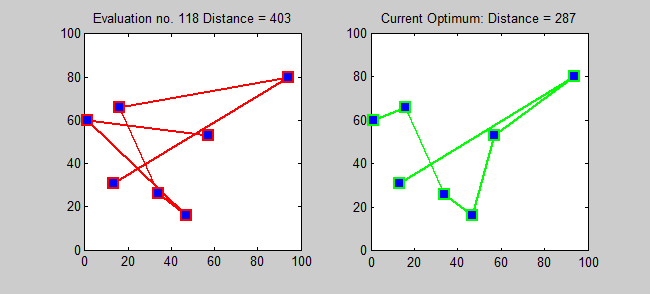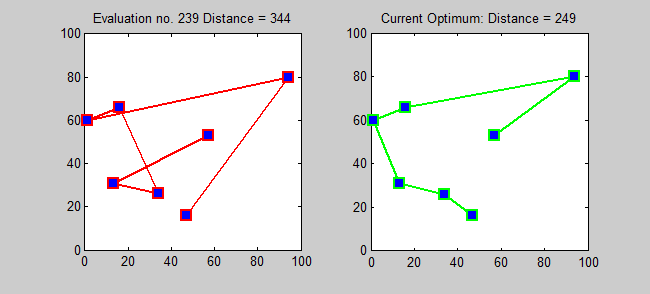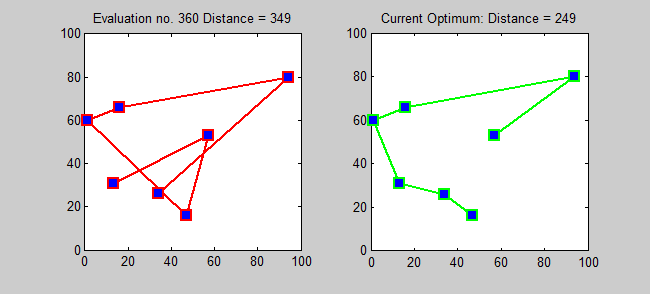
Idée clé
L'algorithme d'approximation pour TSP est un algorithme gourmand (CLRS P1114). Ici, je veux également introduire un algorithme exact pour TSP en utilisant la programmation dynamique.
Sous-problème: pour chaque destination j ∈ {1,2, ..., n}, chaque sous-ensemble s ⊆ {1,2, ..., n} qui contient 1 et j, que ls, j = longueur minimale d'un chemin de 1 à j qui visite précisément les sommets de s [exactement une fois chaque]. Ainsi, récidive correspondante:
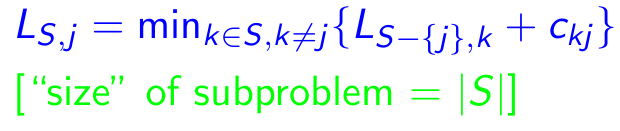
Propriétés
Back to Top Le 3-SAT est l'un des 21 NP complete de KARP, et il est utilisé comme point de départ pour prouver que d'autres problèmes sont également durs NP.
Ici, je présente l'algorithme de Papadimitriou pour 2-SAT (c'est un algorithme très très intéressant , donc je décide de l'introduire même si 2-SAT n'est pas NPC).
Idée clé
Choisissez une affectation initiale aléatoire et choisissez une clause arbitraire non satisfaite et retournez la valeur de l'une de ses variables. Voici le pseudocode:

Une telle affaire occasionnelle avec des clauses nous donnerait étouffément une très grande probabilité de trouver la vraie réponse. Le mécanisme réside dans un terme physique (marche aléatoire). Si vous êtes intéressé, je vous recommande fortement de passer par la marche aléatoire liée à Papadimitriou.
Propriétés
Back to Top