このリポジトリは、Pythonを使用して有名なアルゴリズムを実装します。アルゴリズムは、使用される戦略に従って配置されます。各アルゴリズムには、解決しようとする問題と関連するリソースの説明があります。
(このリポジトリの目標は、私がレビューしたこれらすべての素晴らしいアルゴリズムのために美しい読み取りを作成することです。)
コンテンツ:
このセクションでは、有名な分裂と征服戦略について説明し、この戦略のいくつかのアプリケーションを示します。
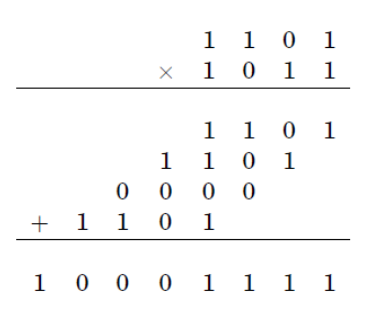
2つのN桁の数値を乗算するための標準手順には、比例した多くの基本操作が必要です。 Karatsubaのアルゴリズムについては、最大で実行時間を短縮します
重要なアイデア
Karatsubaのアルゴリズムの基本的なステップは、2つの多数の積を計算し、それぞれが約半分の数字の数字を持つ3つの多数の乗算を使用することを可能にする式であり、さらにいくつかの追加と数字のシフトがあります。
プロパティ
Back to Top
このアルゴリズムの最悪の実行時間はです。
上記のGIFは、マージソートがどのように機能するかを示しています。 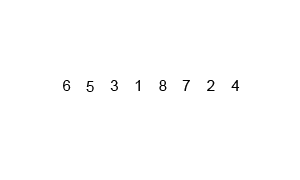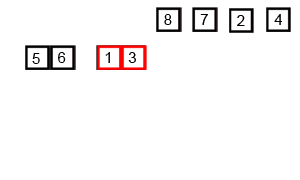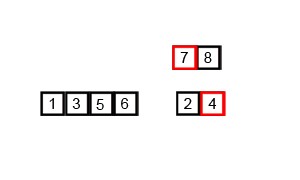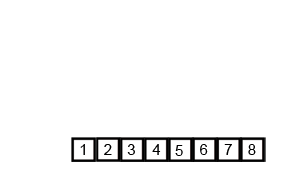
重要なアイデア
アンソートリストをNサブリストに分割し、それぞれに1つの要素(1つの要素のリストがソートされていると見なされ)を含み、サブリストが1つしか残っていないまで、新しいソートサブリストを生成するためにサブリストを繰り返し統合します。これがソートされたリストになります。
プロパティ
Back to Top
重要なアイデア
上の図のように、マージ操作で右サブアレイから最初に要素を取り入れるとき、右要素が(左サブアレイの長さ - 左要素のインデックスの長さ)要素よりも小さいことを示します。
アルゴリズムが進行すると、すべての反転が合計反転を与えます。
プロパティ
Back to Top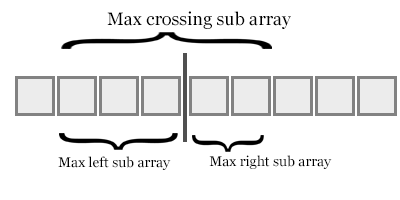
プロパティ
Back to Topこのセクションでは、内部でランダム変数を使用した2つのアルゴリズムについて説明します。
重要なアイデア
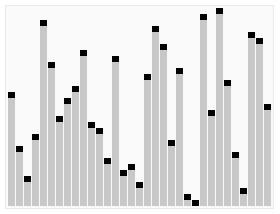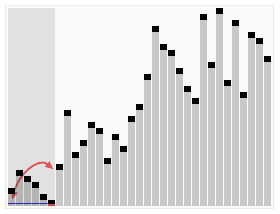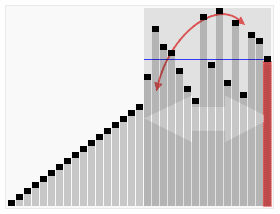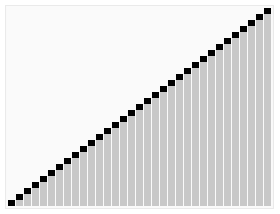
QuickSortは、最初に大きな配列を2つの小さなサブアレイに分割します。ランダムに選択された要素に対する低要素と高要素です。 QuickSortは、サブアレイを再帰的にソートできます。したがって、クイックソートの重要なポイントは、パーティション要素を選択することです。
プロパティ
Back to Top
重要なアイデア
独立したランダム選択で収縮アルゴリズムの時間を繰り返し、最小のカットを返すことにより、最小限のカットを見つけない可能性はです
プロパティ
Back to Topデータ構造を独立したセクションとして配置することは誤解を招くものです。ただし、データ構造によってエレガントに解決される困惑の問題を紹介します。一部のデータ構造には、まだレビューされていないアルゴリズム設計戦略がある場合があります。
重要なアイデア
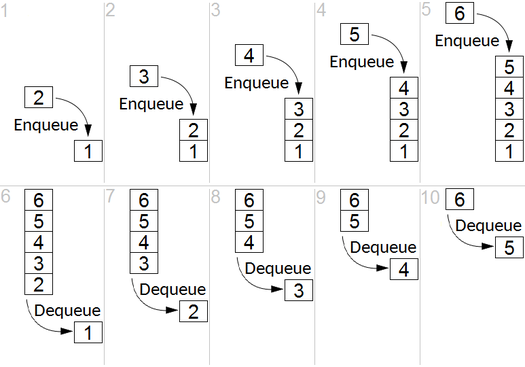
BFSは、無向または指示グラフのソースノードからのリーチ可能なノードをカウントするために使用されます。到達可能なノードが見つかった順序で印刷されます。キューは、ノードカラーグレーを保存するために使用されます(以下のGIFを参照)。 BFSの「幅」という用語は、最も短い長さの到達可能なノードを見つけることを意味します。幅は、訪問したノードと未発見のノードとの境界を拡張します。
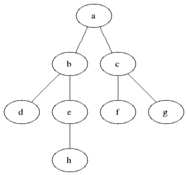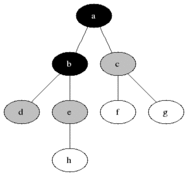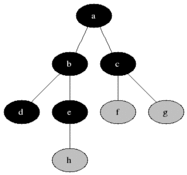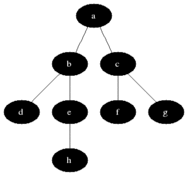
プロパティ
Back to Top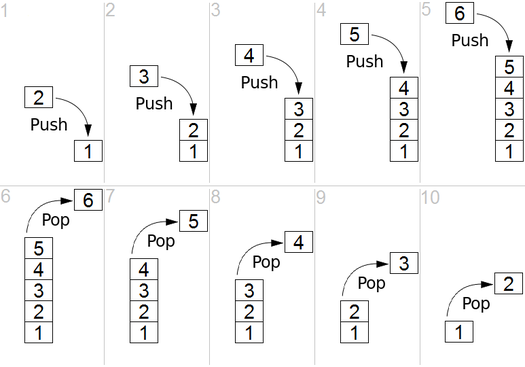
重要なアイデア
DFSは指向グラフで使用され、ソースノードがいくつのノードにアクセスできるかを示し、それらを見つけた順序でそれらを印刷します。スタックを使用して、グラフの開始点として分類されるノードを保存します。その名前の「深さ」は、このアルゴリズムが特定のソースに対してできる限り深く進むことを意味し、エンドポイントに到達すると、開始ノードに戻ります。
プロパティ
Back to Top
メンテナンスの問題の中央値は、整数がデータストリームから読み取られている場合、効率的な方法でそのように読み取られる要素の中央値を見つけることです。簡単にするために、重複はないと仮定します。
重要なアイデア
左側の最大ヒープを使用して、有効な中央値よりも低い要素を表し、右側に最小ヒープを表して、有効な中央値よりも大きい要素を表すことができます。 2つのヒープのサイズの違いが2に大きい場合、1つの要素を別の小さなサイズのヒープに切り替えます。
プロパティ
Back to Top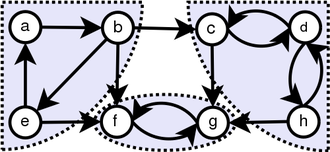
重要なアイデア
単純な観察を通じて、グラフのTranposeが元のグラフと同じSCCを持っていることがわかります。 DFSを2回実行します。初めて、それをGで実行し、各頂点の仕上げ時間を計算します。そして、G^tでDFSを実行しますが、DFSのメインループでは、終了時間を短縮する順に頂点を検討します。
プロパティ
Back to Top
重要なアイデア
無向グラフでは、このデータ構造を使用して、SCCの数を確認できます。下の図は、それがどのように機能するかを示しています。
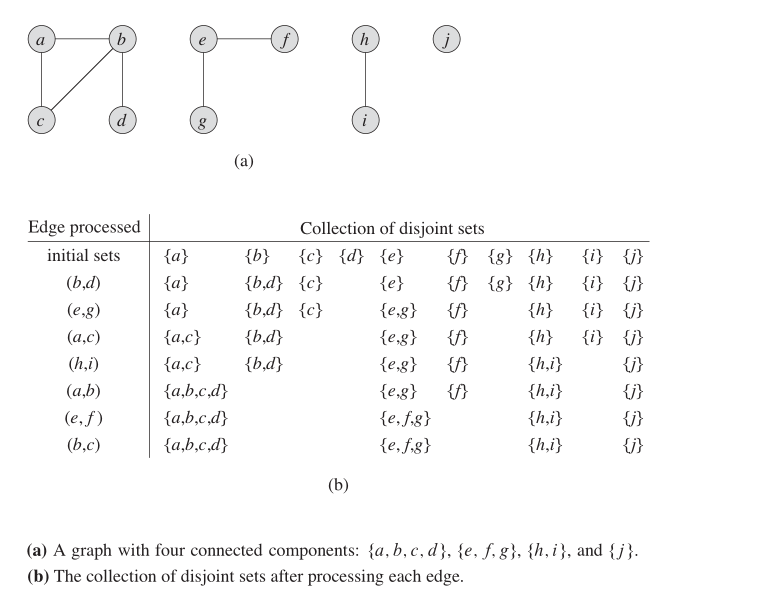
プロパティ
Back to Topこのセクションでは、1つの強力なアルゴリズム設計戦略である貪欲なアルゴリズムを紹介します。
ウィキペディアから、貪欲なアルゴリズムは、グローバルな最適を見つけることを期待して、各段階で局所的に最適な選択をするという問題を解決する問題を解決することに続くアルゴリズムのパラダイムです。多くの問題で、貪欲な戦略は一般に最適なソリューションを生み出すわけではありませんが、それでも貪欲なヒューリスティックは、合理的な時期にグローバルな最適なソリューションを近似する局所的に最適なソリューションをもたらす可能性があります。
アクティビティ選択の問題では、すべてのアクティビティには独自の重量と長さがあります。そして、私たちの目標は、重量*の長さの合計を最小限に抑えることです。貪欲なアルゴリズムがどのように機能するかを示すのは非常に簡単で素晴らしい例です。
重要なアイデア
値の重み/長さでアクティビティを並べ替えると、既存の最適構造がこの配置よりも優れていないことを証明できます。 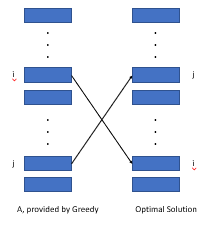
上記の図に示すように、2つの配置(i、j)で異なる範囲の2つのアクティビティによって引き起こされるコストを考慮します。貪欲なアルゴリズムのコストは、wi*lj -wj*liの値によって最適構造よりも小さく、0以上のものであることがわかります。
プロパティ
Back to Top
重要なアイデア
仕上げ時間に従って配列をソートしました。アルゴリズムは、最初のジョブの最初のジョブを最後のジョブの終了時間よりも大きくしました。
プロパティ
Back to Top
この本をエンコードする1つの方法は、固定長さのコーディングを使用することです。以下に示すように:
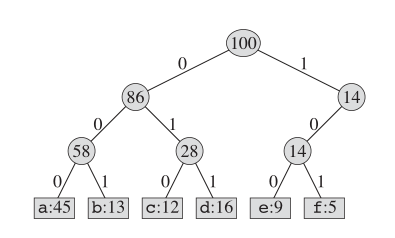
ハフマンコーディングに関しては、実際のツリー構造は次のようになります。
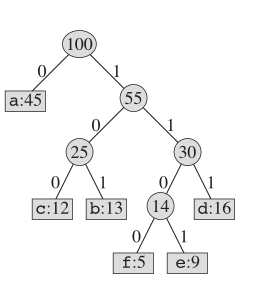
重要なアイデア
バイナリツリーを維持し、2つの最小限の文字の親として新しいノードを作成します。そして、この新しいノードの鍵は、2人の子供のキーの合計です。この「本」にノードが残されないまでこれを繰り返します。
プロパティ
Back to TopDijkstraのアルゴリズムは、グラフ内のノード間の最短パスを見つけるためのアルゴリズムです。ただし、1つの前提条件があり、すべてのパスは0以下である必要があります。
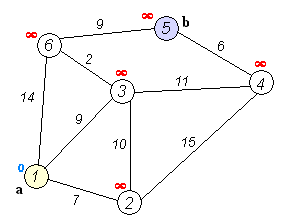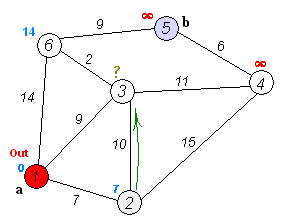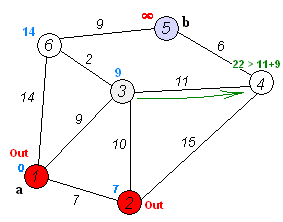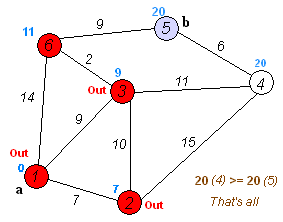
重要なアイデア
ノードを2つのグループに分け、1つのグループが調査されているようにマークされます。そして、未開拓のグループから探索したグループへの距離を最短距離で更新します。
プロパティ
Back to Top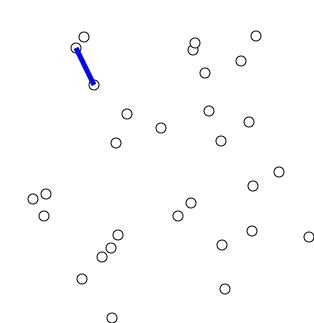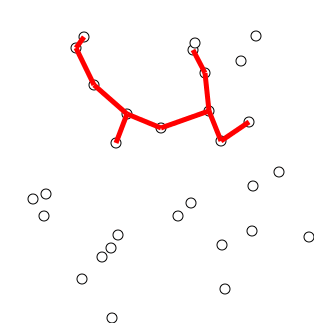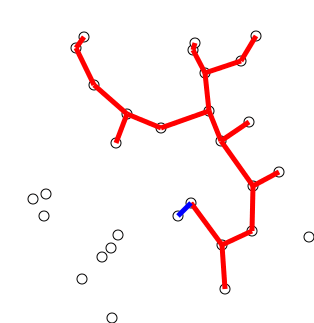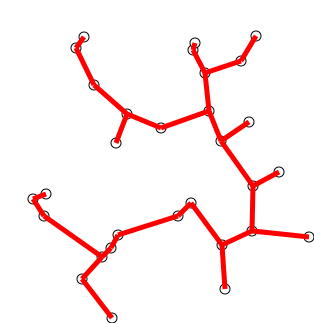
重要なアイデア
アルゴリズムは、非公式に次の手順を実行すると説明できます。
グラフから任意に選択された単一の頂点でツリーを初期化します。
ツリーを1つの端で成長させます。ツリーをツリーにまだ頂点に接続するエッジのエッジを、最小重量のエッジを見つけて、木に移します。
ステップ2を繰り返します(すべての頂点がツリー内にあるまで)。
プロパティ
Back to Top
重要なアイデア
SCCと非常によく似ていますが、グラフのクラスの数を制御するためにAlogrithmを早期に停止できます。つまり、グラフをクラスターすることができます。
プロパティ
Back to Topこのセクションでは、1つの強力なアルゴリズム設計戦略である動的アルゴリズムを紹介します。
ウィキペディアから、動的プログラミング(動的最適化とも呼ばれます)は、それをより単純なサブ問題のコレクションに分解し、それらの各サブ問題を1回だけ解決し、ソリューションを保存することにより、複雑な問題を解決する方法です。
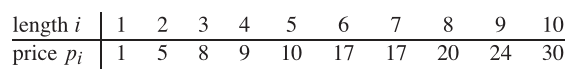
したがって、ロッドの長さが8で、異なるピースの値が次のように与えられている場合、最大取得可能な値は22です(長さ2と6の2つのピースを切断することにより)。
重要なアイデア
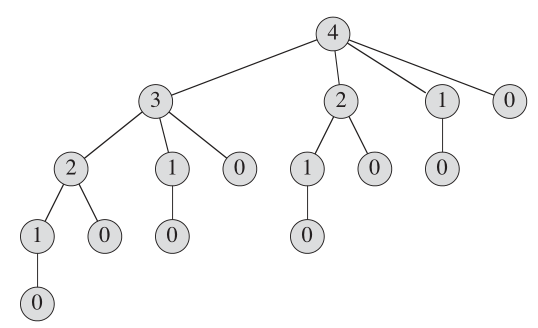
分解は、左側の端を切り取った最初の長さの長さで構成され、次に長さn-iの右側の残りで構成されると考えています。だから、擬似コードは次のように見えます:
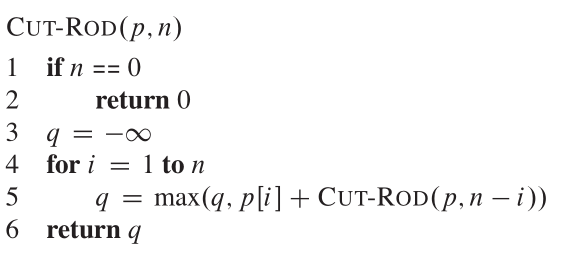
コールCUT_ROD(P、N)に起因する再帰コールを示す再帰ツリーは次のように見えます。
小さなサブ問題の繰り返し計算を保存するために、これらの値を保存するための配列を記憶しました。
プロパティ
Back to Top
重要なアイデア
最適な構造:
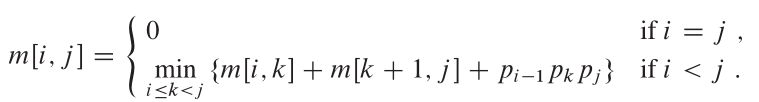
プロパティ
Back to Top重要なアイデア
CLRSから、この問題の最適な構造は次のとおりです。
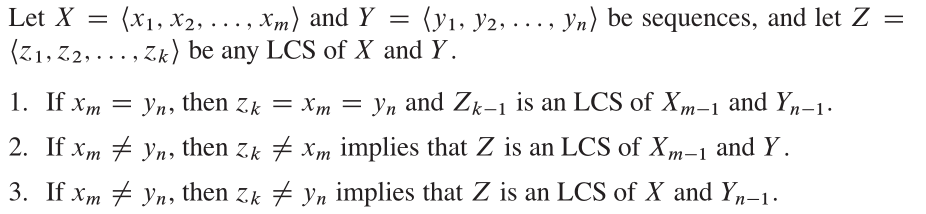
プロパティ
Back to Top重要なアイデア
このアルゴリズムは、非常に直感的な観察に基づいています。元の頂点グループ{1、2、3、...、n}のサブセット{1、2、3、4、...、k}(v(k)として示される)があるとします。 PがV(k)でiからJへの最短経路である場合、2つのケースがあります。まず、KがPにない場合、PはV(K-1)で最短経路でなければなりません。第二に、kがPにある場合、パスを2つに分離することができます、p1:i K、P2:k j。 P1は、v(k-1)でiからkまでの最短経路でなければなりません。P2は、kからjまでのkまでの最短経路でなければなりません。
プロパティ
Back to TopWikipediaから、NP完全な決定問題は、NPとNPハードの複雑さの両方に属するものです。これに関連して、NPは「非決定論的多項式時間」の略です。 NP不完全な問題のセットは、多くの場合、NP-CまたはNPCで示されます。
このセクションでは、3つの非常に有名なNPC問題を導入し、近似アルゴリズムを説明してそれらにアプローチします。
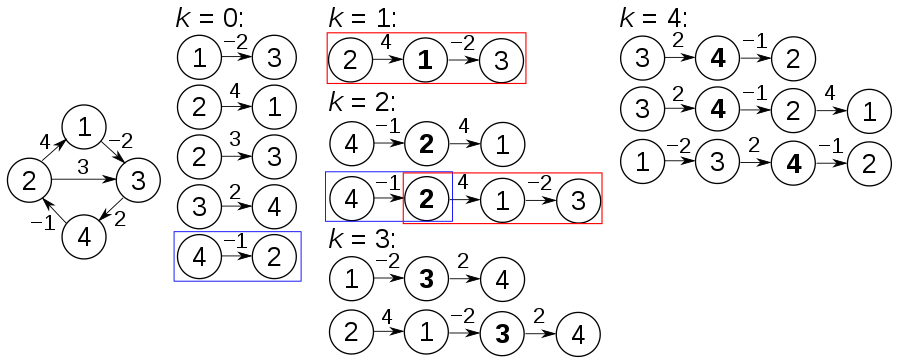
重要なアイデア
最小の頂点カバーを見つけることは非常に困難ですが、多項式時間の最大2倍の頂点でおおよそのカバーを見つけることができます。

プロパティ
Back to Top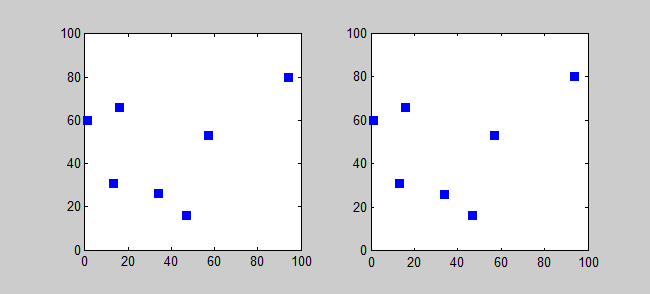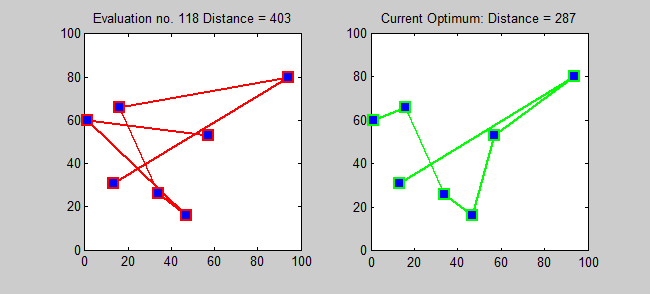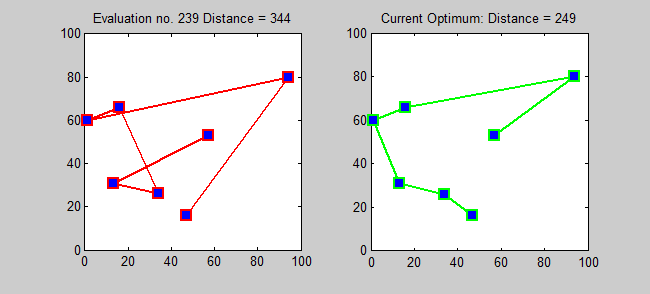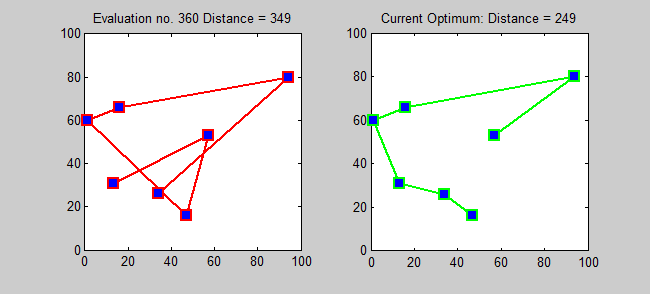
重要なアイデア
TSPの近似アルゴリズムは、貪欲なアルゴリズムです(CLRS P1114)。ここでは、動的プログラミングを使用してTSPの正確なアルゴリズムも紹介したいと思います。
問題:すべての宛先J∈{1,2、...、n}、すべてのサブセットs⊆{1,2、...、n}を含むすべてのサブセットs⊆、jを含む、ls、j = 1からjまでのパスの最小長さは、sの頂点を正確に訪れる[1回は1回]。したがって、対応する再発:
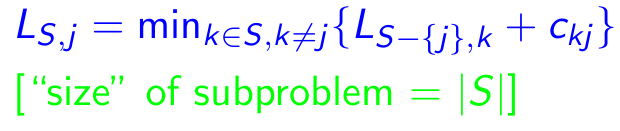
プロパティ
Back to Top 3-SATは、KARPの21のNP完全な問題の1つであり、他の問題もNPハードであることを証明するための出発点として使用されます。
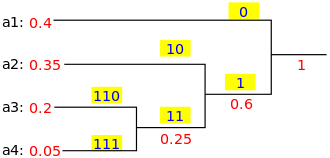
ここでは、2-SATのPapadimitriouのアルゴリズムを紹介します(これは非常に非常に興味深いアルゴリズムなので、2-SATはNPCではない場合でも導入することにしました)。
重要なアイデア
ランダムな初期割り当てを選択し、任意の不満の句を選択し、その変数の1つの値をひっくり返します。これが擬似コードです:

このようなカジュアルな条項との取引は、驚くべきことに、本当の答えを見つける可能性が非常に大きいでしょう。メカニズムは物理学用語(ランダムウォーク)にあります。興味のある方は、パパディミトリウとのランダムウォークにどのように関連しているかを確認することを強くお勧めします。
プロパティ
Back to Top