algorithms in python

algorithms-in-python

This repository, I will use Python to implement some famous algorithms. The algorithms are arranged according to the strategy used. Each algorithm will have an explanation to the problem it attempts to solves and some relevant resources.
(The goal of this repository is to create a beautiful README for all of these brilliant algorithms that I have reviewed.)

Content:

• 1.0 - Divide and Conquer
  • 1.1 - Interger Multiplication Problem
  • 1.2 - Merge Sort (and Insertion Sort)
  • 1.3 - Count Inversions
  • 1.4 - Maximum Subarray
• 2.0 - Randomized Algorithms
  • 2.1 - Quick Sort
  • 2.2 - Karger's Algorithm
• 3.0 - Data Structures
  • 3.1 - Queue and Breadth First Search
  • 3.2 - Stack and Depth First Search
  • 3.3 - Heap and Median Median Maintenance
  • 3.4 - Strongly Connected Component
  • 3.5 - Disjoint-set and SCC
• 4.0 - Greedy Algorithms
  • 4.1 - Shedule Activities
  • 4.2 - Activity selection
  • 4.3 - Huffman Coding
  • 4.4 - Dijkstra's Algorithm
  • 4.5 - Prim's Algorithm
  • 4.6 - Kruskal's Algorithm and Clustering Problem
• 5.0 - Dynamic Programming
  • 5.1 - Rod Cutting
  • 5.2 - Matrix Chain Multiplication
  • 5.3 - Longest Common Subsequence
  • 5.4 - Floyd-Warshall Algorithm
• 6.0 - Approximation Algorithms for NPC
  • 6.1 - Vertex Cover
  • 6.2 - Travelling Salesman Problem
  • 6.3 - Boolean Satisfiability Problem

1.0 - Divide and Conquer

This section, I will talk about the famous divide and conquer strategy and show some applications of this strategy.

1.1 - Interger Multiplication Problem

• Useful Link
  

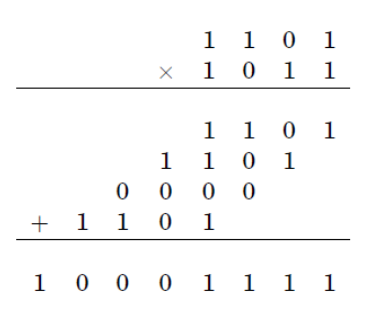
The standard procedure for multiplication of two n-digit numbers requires a number of elementary operations proportional to . As for The Karatsuba algorithm, it reduces the running time to at most

Key idea
The basic step of Karatsuba's algorithm is a formula that allows one to compute the product of two large numbers and using three multiplications of smaller numbers, each with about half as many digits as or , plus some additions and digit shifts.
Properties

• Running Time:
  Back to Top

1.2 - Merge Sort (and Insertion Sort)

• Useful Link
  Before we discuss merge sort, the insertion sort algorithm will be analyzed and its running time to appreciate merge sort. The picture below shows the intuitive idea for sorting is to imitate how cards are arranged according to its size. When we receive a card, we immediately arrange it based on other cards in our hand.

The worst running time for this algorithm is .
Gif above shows how merge sort works:

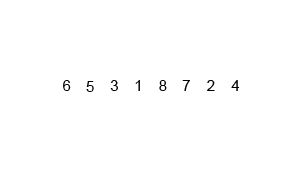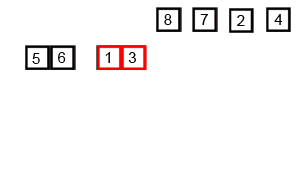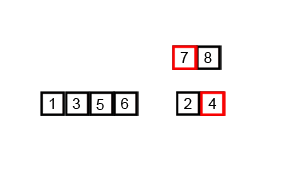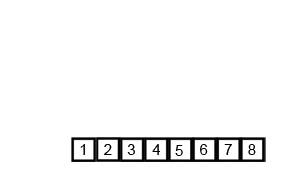
Key idea
Divide the unsorted list into n sublists, each containing 1 element (a list of 1 element is considered sorted) and repeatedly merge sublists to produce new sorted sublists until there is only 1 sublist remaining. This will be the sorted list.
Properties

• Running Time:
  Back to Top

1.3 - Count Inversions

• Useful Link
  Actually, this can be treated as application of Merger Sort. Every time we do merge operation in merge sort, we implicitly calculate the inversions.
  

Key idea
Like the figure above, when we first take in element from right sub-array in merge operation, that indicates the right element is smaller than ( length of left sub-array - the index of left element) elements.
As the algorithm progresses, add all the inversions will give us the total inversions.
Properties

• Running Time:
  Back to Top

1.4 - Maximum Subarray

• Useful Link
  The maximum subarray problem is the task of finding the contiguous subarray within a one-dimensional array, a[1...n], of numbers which has the largest sum.
  Key idea
  If we use the divide and conquer strategy, if the array is A[low..high] and the middle point is represented as mid. A[i..j]is what we want to calculate. A[i..j] has to be one of the three cases:
  

• A[i..j] belongs to A[low..mid]
• A[i..j] belongs to A[mid+1..high]
• i <= mid < j
  So, our job is to find the largest sub array crossing the mid point and choose the largest one among these three algorithms.

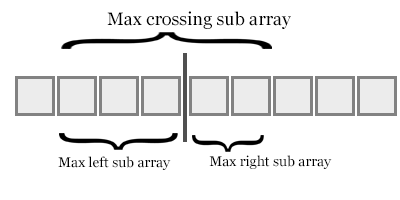
Properties

• Running Time:
  Back to Top

2.0 - Randomized Algorithms

This section I will talk about two algorithms which has used random variable inside.

2.1 - Quick Sort

• Useful Link
  

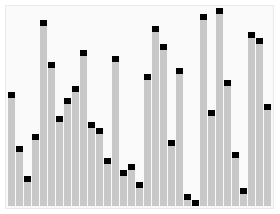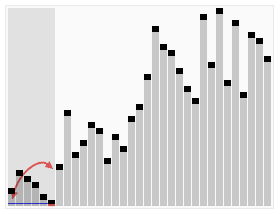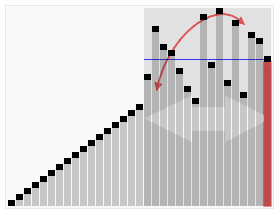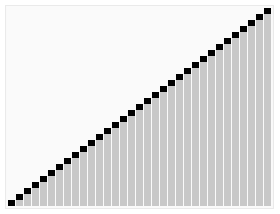
Key idea
Quicksort first divides a large array into two smaller sub-arrays: the low elements and the high elements relative to a randomly chosen element. Quicksort can then recursively sort the sub-arrays. So, the key point in quick sort is to choose partition element.
Properties

• Worst case performance O(n^2)
• Best case performance O(n log n) or O(n) with three-way partition
• Average case performance O(n log n)
  Back to Top

2.2 - Karger Algorithm

• Useful Link
  The idea of the algorithm is based on the concept of contraction of an edge (u,v) in an undirected graph G=(V,E). Informally speaking, the contraction of an edge merges the nodes u and v into one, reducing the total number of nodes of the graph by one. The figure below shows how contraction works. In the sub figure left, two Bold Black nodes are fused into one (the sub figure in the right).

Key idea
By repeating the contraction algorithm times with independent random choices and returning the smallest cut, the probability of not finding a minimum cut is
Properties

• With high probability we can find all min cuts in the running time of
• Not finding a min cut probability is times.
  Back to Top

3.0 - Data Structures

To place data structures as an independent section is misleading; however, I will introduce perplexing problems which are elegantly solved by data structures. Some data structures may have an algorithm design strategy that have not been reviewed yet.

3.1 - Queue and Breadth First Search

• Useful Link1 Link2
  Queue, also known as FIFO, is an acronym for first in, first out, a method for organizing and manipulating a data buffer, where the oldest (first) entry, or 'head' of the queue, is processed first.

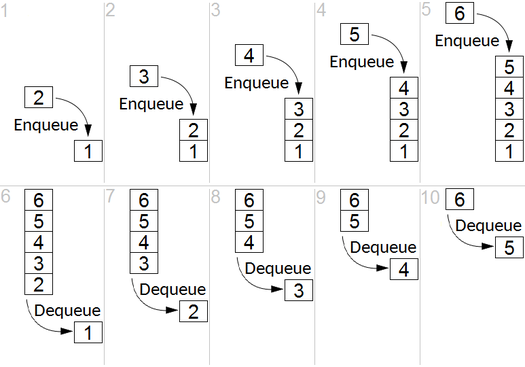
Key idea
BFS is used to count reachable nodes from a source node in a undirected or directed graph. Reachable nodes are printed in the order found. A queue is used to store the nodes colored grey (see the gif below). The term "breadth" in BFS means finding a reachable node with the shortest length. The breadth extends the border between the visited nodes and the undiscovered nodes.

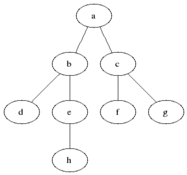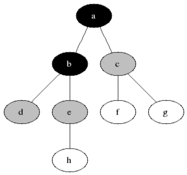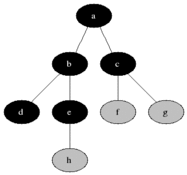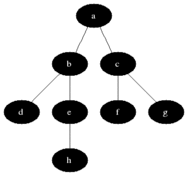
Properties

• Running Time: T(n)= O(V+E), V is number of vertices, E is number of edges
  Back to Top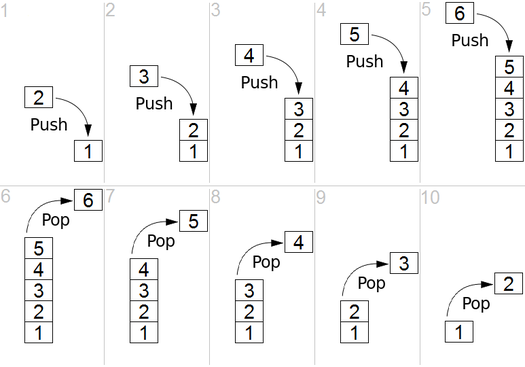

3.2 - Stack and Depth First Search

• Useful Link1 Link2
  Stack, also known as LIFO, has the property of last in, first out.
  

Key idea
And DFS is used in directed graph and it tells how many nodes a source node can reach and print them out by the order we find them. We use stack to store the nodes we classify as the start points for graph. The "depth" in its name means that this algorithm will go as deeply as it can for a given source and when it reaches the endpoint, it returns to the start node.

Properties

• Running Time: T(n)= O(V+E), V is number of vertices, E is number of edges
  Back to Top

3.3 - Heap and Median Median Maintenance

• Useful Link1 Link2
  Heap is a specialized tree-based data structure that satisfies the heap property: if P is a parent node of C, then the key (the value) of P is either greater than or equal to (in a max heap) or less than or equal to (in a min heap) the key of C.[1] The node at the "top" of the heap (with no parents) is called the root node.

Median Maintenance problem is that if integers are read from a data stream, find median of elements read so for in efficient way. For simplicity assume there are no duplicates.

Key idea
We can use a max heap on left side to represent elements that are less than effective median, and a min heap on right side to represent elements that are greater than effective median. When the difference between size of two heaps is greater or equal to 2, we switch one element to another smaller size heap.

Properties

• Running Time:
  Back to Top

3.4 - Strongly Connected Component

• Useful Link
  A directed graph is called strongly connected if there is a path in each direction between each pair of vertices of the graph. In a directed graph G that may not itself be strongly connected, a pair of vertices u and v are said to be strongly connected to each other if there is a path in each direction between them.

Key idea
Through simple observation, we find out that tranpose of graph has the same SCCs as the original graph. We run DFS twice. First time, we run it on G and compute finishing time for each vertex. And then, we run DFS on G^T but in the main loop of DFS, consider the vertices in order of decreasing finishing time.
Properties

• Running Time: , V is number of vertices, E is number of edges
  Back to Top

3.5 - Disjoint-set and SCC

• Useful Link
  A disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that keeps track of a set of elements partitioned into a number of disjoint (non-overlapping) subsets.
  For a naive disjoint-set, it supports two main operations, Make-Set and Union. Make-set make every vertex an independent group. Union puts two vertices in one group.

Key idea
In an undirected graph, we can use this data structure to find out how many SCCs. The figure below shows how it works.

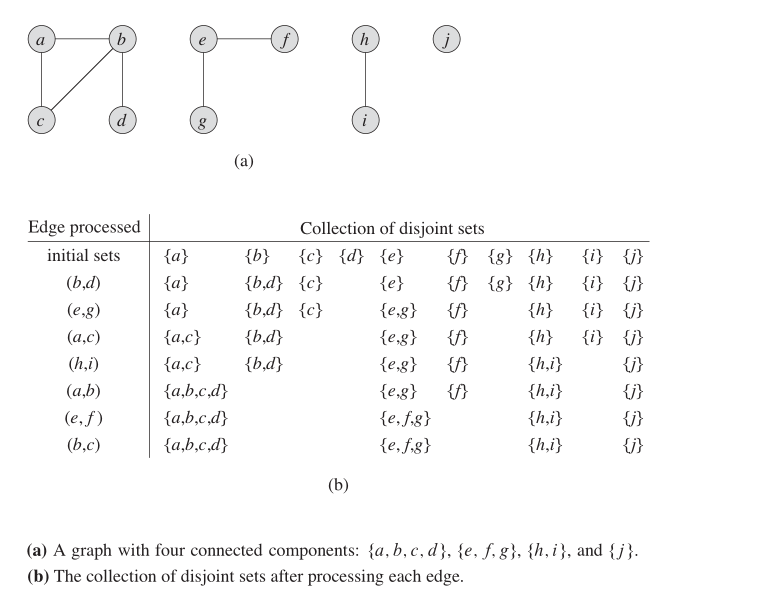
Properties

• We can use a weighted-union heuristic to save time when call find_set operation
• Path compression can greatly improve time efficiency of union find
  Back to Top

4.0 - Greedy Algorithms

In this section, I'm going to introducce greedy algorithms, one powerful algorithm design strategy.
From Wikipedia, a greedy algorithm is an algorithmic paradigm that follows the problem solving heuristic of making the locally optimal choice at each stage[1] with the hope of finding a global optimum. In many problems, a greedy strategy does not in general produce an optimal solution, but nonetheless a greedy heuristic may yield locally optimal solutions that approximate a global optimal solution in a reasonable time.

4.1 - Shedule Activities

In activity selection problem, every activity has its own weight and length. And our goal is to minimize the sum of weight*length. It is a very easy and great example to show how greedy algorithm works and provide an elegant proof using argument exchange technique.
Key idea
If we sort activity by value weight/length, we can prove an existing optimal structure cannot be better than this arrangement.

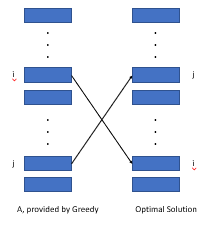
As the figure shown above, we consider the cost caused by two activities that are ranged differently in two arrangement (i, j). We find out that the cost in greedy algorithm is smaller than optimal structure by the value of wi*lj - wj*li, which is greater than or equal to 0.

Properties

• Running time is dominated by sorting
  Back to Top

4.2 - Activity selection

• Useful Link
  In this problem, every activity has its own start time and finish time. our goal is to selection a max-length subset, where jobs are compatible.
  

Key idea
We sorted the array according to its finish time. The algorithm put the first job whose start time is bigger than last job's finish time.
Properties

• The recursive activity selection running time is
  Back to Top

4.3 - Huffman Coding

• Useful Link
  Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. For example, the table below shows letters' frequency in a "book".

One way to encode this book is to use fixed length coding. As shown below:

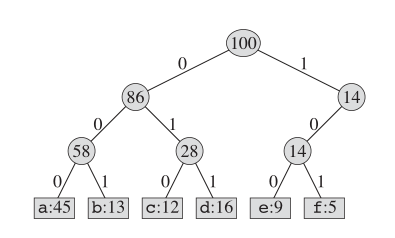
As for huffman coding, the actual tree structure looks like this:

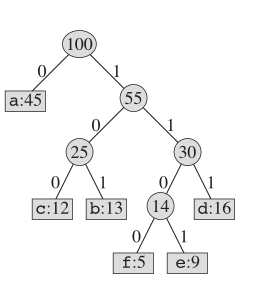
Key idea
We maintain a binary tree and create a new node as the parent for two least-frequent letters. And the key for this new node is the sum of keys for its two children. We repeat this until no nodes left in this "book".

Properties

• Procedure HUFFMAN produces an optimal prefix code
  Back to Top

4.4 - Dijkstra Algorithm

• Useful Link
  

Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a graph. However, it has one prerequisite, all paths have to be greater or equal to 0.

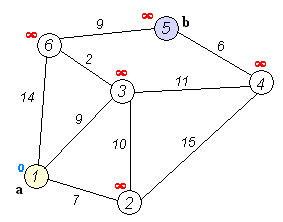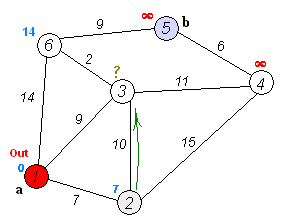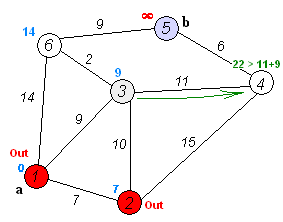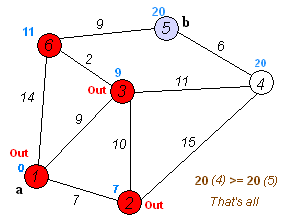
Key idea
Separate nodes into two groups, one group is marked as explored. And we update the distance from unexplored group to explored group by the shortest distance.

Properties

• Running time based on a min-priority queue implemented by a Fibonacci heap
  Back to Top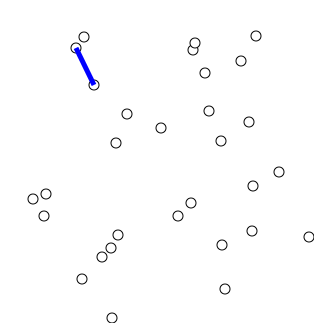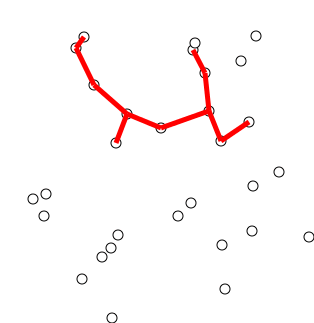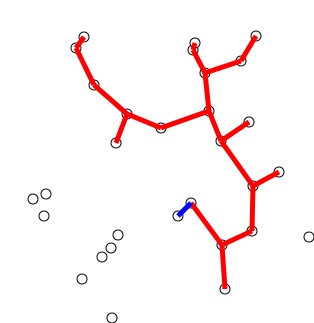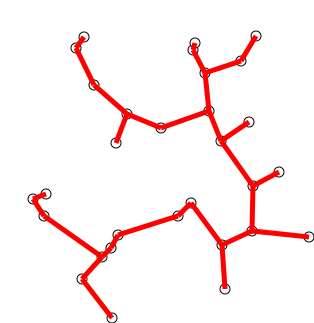

4.5 - Prim Algorithm

• Useful Link
  Prim's algorithm is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph. Very similar to Dijkstra Algorithm, we maintain two sets, explored one and unexplored one. Every time, we only absorb the vertex, which has the smallest distance to explored set. This is shown very clearly in the figure below:

Key idea
The algorithm may informally be described as performing the following steps:

Initialize a tree with a single vertex, chosen arbitrarily from the graph.
Grow the tree by one edge: of the edges that connect the tree to vertices not yet in the tree, find the minimum-weight edge, and transfer it to the tree.
Repeat step 2 (until all vertices are in the tree).

Properties

• Running time

• adjacency matrix, searching
• binary heap and adjacency list
• Fibonacci heap and adjacency list
  Back to Top

4.6 - Kruskal Algorithm and Clustering Problem

• Useful Link
  Prim's algorithm is another greedy algorithm that finds a minimum spanning tree for a weighted undirected graph. Instead of maintaining a tree like Prim, it maintains forest.

Key idea
Very similar to SCC, we can early stop the alogrithm to control number of classes in our graph, which is to say we can cluster the graph.

Properties

• Running time O(ElogV)
  Back to Top

5.0 - Dynamic Programming

In this section, I'm going to introduce dynamic algorithms, one powerful algorithm design strategy.
From Wikipedia, dynamic programming (also known as dynamic optimization) is a method for solving a complex problem by breaking it down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions.

5.1 - Rod Cutting

• Useful Link
  Given a rod of length n inches and an array of prices that contains prices of all pieces of size smaller than n. Determine the maximum value obtainable by cutting up the rod and selling the pieces.
  The following table shows the relationship between price and length.

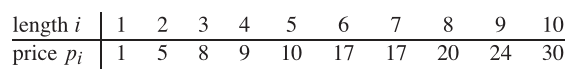
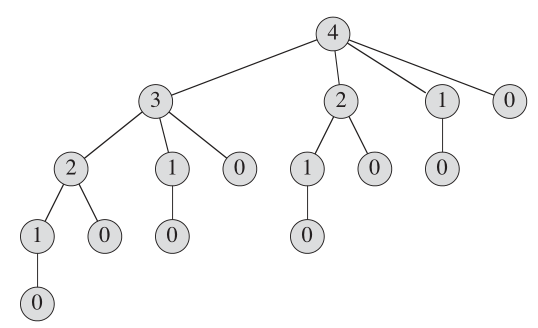
So, if length of the rod is 8 and the values of different pieces are given as following, then the maximum obtainable value is 22 (by cutting in two pieces of lengths 2 and 6).

Key idea
We view a decomposition as consisting of a first piece of length i cut off the left-hand end, and then a right-hand remainder of length n - i. So, the pseudocode looks like:

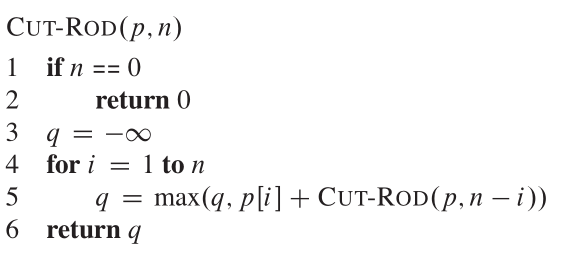
The recursion tree showing recursive calls resulting from a call CUT_ROD(p, n) looks like:

In order to save the repeated computation for small sub-problems, we memorized an array to store these values.

Properties

• Time Complexity of the above implementation is O(n^2)
  Back to Top

5.2 - Matrix Chain Multiplication

• Useful Link
  Matrix chain multiplication (or Matrix Chain Ordering Problem, MCOP) is an optimization problem that can be solved using dynamic programming. Given a sequence of matrices, the goal is to find the most efficient way to multiply these matrices. The problem is not actually to perform the multiplications, but merely to decide the sequence of the matrix multiplications involved.

Key idea
Optimal structure:

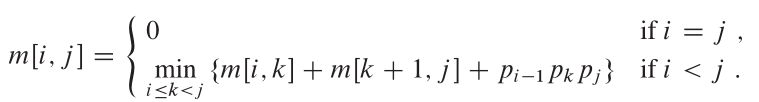
Properties

• Time Complexity of the above implementation is
  Back to Top

5.3 - Longest Common Subsequence

• Useful Link
  The longest common subsequence (LCS) problem is the problem of finding the longest subsequence common to all sequences in a set of sequences (often just two sequences).

Key idea
From CLRS, the optimal structure for this problem is:

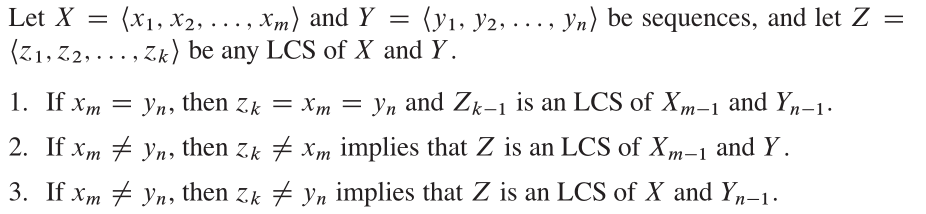
Properties

• Time Complexity of the above implementation is $theta(mn)$
  Back to Top

5.4 - Floyd-Warshall Algorithm

• Useful Link
  Floyd–Warshall algorithm is an algorithm for finding shortest paths in a weighted graph with positive or negative edge weights (but with no negative cycles).

Key idea
This algorithm is based on very intuitive observation. Suppose we have a subset {1, 2, 3, 4, ..., k} (denote as V(k)) of original vertices group {1, 2, 3, ..., n}. If p is a shortest path from i to j in V(k), we have two cases. First, if k is not in p, then p must be a shortest path in V(k-1). Second, if k is in p, then we can seperate the path into two, P1: ik, P2:kj. and P1 must be the shortest path from i to k with V(k-1), P2 must be the shortest path from k to j with V(k-1).

Properties

• Time Complexity of the above implementation is
  Back to Top

6.0 - Approximation Algorithms for NPC

From From Wikipedia, an NP-complete decision problem is one belonging to both the NP and the NP-hard complexity classes. In this context, NP stands for "nondeterministic polynomial time". The set of NP-complete problems is often denoted by NP-C or NPC.

In this section, I am going to introduce three very famous NPC problems and explain approximation algorithms to approach them.

6.1 - Vertex Cover

• Useful Link
  A vertex cover (sometimes node cover) of a graph is a set of vertices such that each edge of the graph is incident to at least one vertex of the set. The figure below shows a minimum vertex cover (where the cover set must have at least two vertice, zero and one wouldn't help).

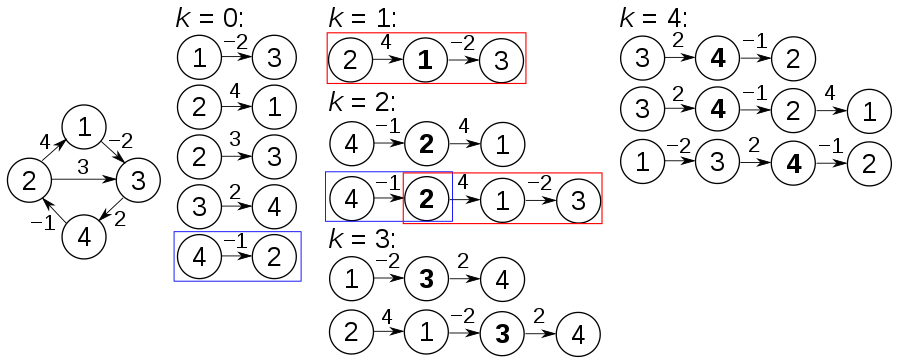
Key idea
It is very difficult to find a minimum vertex cover but we can find a approximate cover with at most twice the vertices in polynomial time.

Properties

• APPROR-VERTEX-COVER is a polynomial-time 2-approximation algorithm.
  Back to Top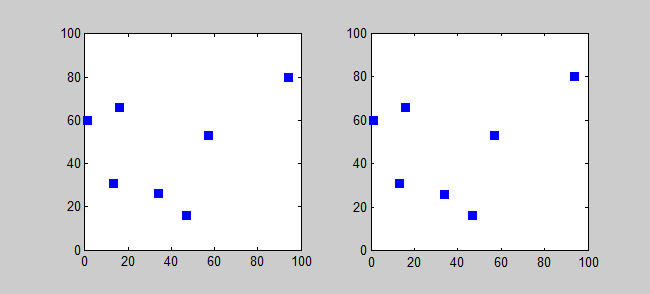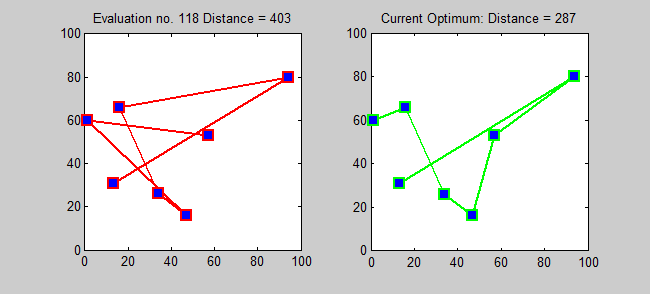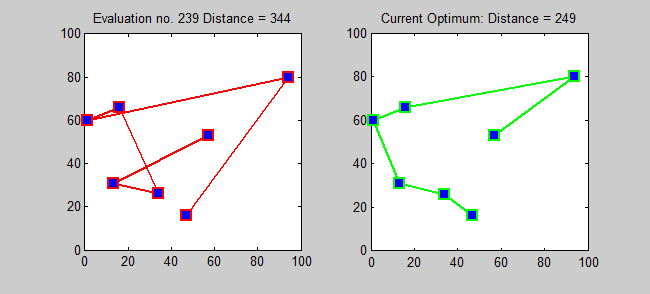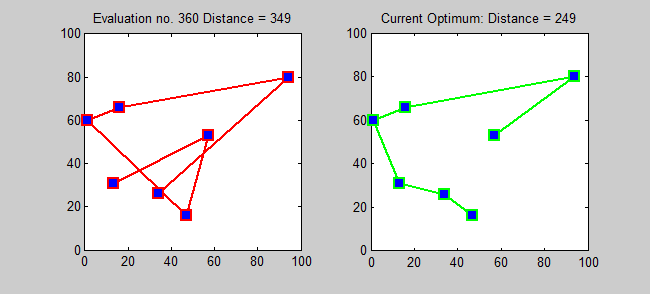

6.2 - Travelling Salesman Problem

• Useful Link
  The travelling salesman problem (TSP) asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?" The gif shows brute force for tsp.

Key idea
The approximation algorithm for tsp is a greedy algorithm (CLRS P1114). Here, I also want to introduce an exact algorithm for tsp using dynamic programming.

Subproblem: for every destination j ∈ {1,2,...,n}, every subset S ⊆ {1,2,...,n} that contains 1 and j, let L S,j = minimum length of a path from 1 to j that visits precisely the vertices of S [exactly once each]. So, Corresponding recurrence:

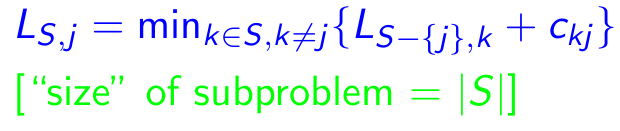
Properties

• Running Time for exact algorithm:
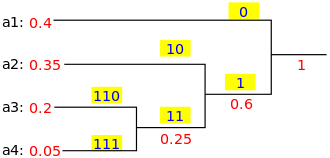
  Back to Top

6.3 - Boolean Satisfiability Problem

• Useful Link
  Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated as SATISFIABILITY or SAT) is the problem of determining if there exists an interpretation that satisfies a given Boolean formula.

3-SAT is one of Karp's 21 NP-complete problems, and it is used as a starting point for proving that other problems are also NP-hard.

Herein, I introduce Papadimitriou’s Algorithm for 2-SAT (This is a very very very interesting algorithm , so I decide to introduce it even though 2-SAT is not NPC).

Key idea
Choose random initial assignment and pick arbitrary unsatisfied clause and flip the value of one of its variable. Here is the pseudocode:

Such a casual dealing with clauses would suprisingly give us a very large probability to find the real answer. The mechanism lies in a physics term (random walk). If you are interested, I strongly recommend you to go through how random walk related to Papadimitriou.

Properties

• For a satisfiable 2-SAT instance with n variables, Papadimitriou’s algorithm produces a satisfying assignment with probability ≥ 1 − 1/n
• Runs in polynomial time
• Always correct on unsatisfiable instances
  Back to Top