Este repositório, usarei o Python para implementar alguns algoritmos famosos. Os algoritmos são organizados de acordo com a estratégia usada. Cada algoritmo terá uma explicação para o problema que tenta resolver e alguns recursos relevantes.
(O objetivo deste repositório é criar um belo ReadMe para todos esses algoritmos brilhantes que eu revisei.)
Contente:
Nesta seção, falarei sobre a famosa estratégia de divisão e conquista e mostrarei algumas aplicações dessa estratégia.
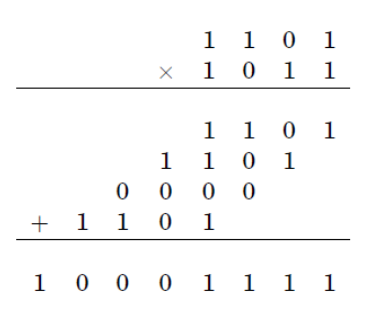
O procedimento padrão para multiplicação de dois números de dígitos N requer várias operações elementares proporcionais a. Quanto ao algoritmo Karatsuba, reduz o tempo de execução para a maioria
Ideia -chave
A etapa básica do algoritmo de Karatsuba é uma fórmula que permite calcular o produto de dois grandes números e usar três multiplicações de números menores, cada um com cerca da metade do mesmo tempo de dígitos que ou, além de algumas adições e mudanças de dígitos.
Propriedades
Back to Top
O pior tempo de execução para esse algoritmo é.
GIF acima mostra como a classificação da mesclagem funciona: 
Ideia -chave
Divida a lista não classificada em n sublistas, cada um contendo 1 elemento (uma lista de 1 elemento é considerada classificada) e mescla repetidamente sublistas para produzir novos sublistas classificados até que haja apenas 1 sublista restante. Esta será a lista classificada.
Propriedades
Back to Top
Ideia -chave
Como a figura acima, quando assumimos o elemento da sub-matriz direita na operação de mesclagem, isso indica que o elemento direito é menor que (comprimento da sub-matriz esquerda-o índice do elemento esquerdo).
À medida que o algoritmo avança, adicione todas as inversões nos dará as inversões totais.
Propriedades
Back to Top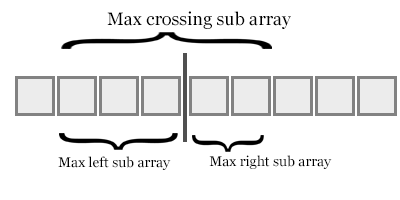
Propriedades
Back to TopNesta seção, falarei sobre dois algoritmos que usaram variável aleatória dentro.
Ideia -chave
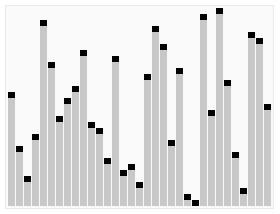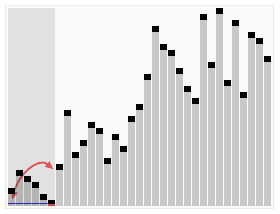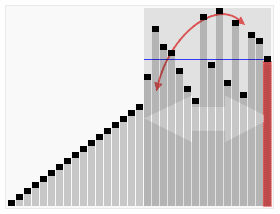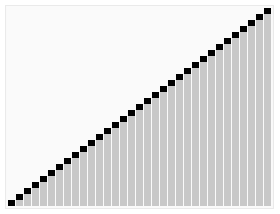
O Quicksort primeiro divide uma grande matriz em dois sub-maiores de teatro: os elementos baixos e os elementos altos em relação a um elemento escolhido aleatoriamente. O Quicksort pode então classificar recursivamente os sub-maiores. Portanto, o ponto principal da classificação rápida é escolher o elemento de partição.
Propriedades
Back to Top
Ideia -chave
Ao repetir o algoritmo de contração com opções aleatórias independentes e retornar o menor corte, a probabilidade de não encontrar um corte mínimo é
Propriedades
Back to TopColocar as estruturas de dados como uma seção independente é enganosa; No entanto, apresentarei problemas desconcertantes que são resolvidos elegantemente por estruturas de dados. Algumas estruturas de dados podem ter uma estratégia de design de algoritmo que ainda não foi revisada.
Ideia -chave
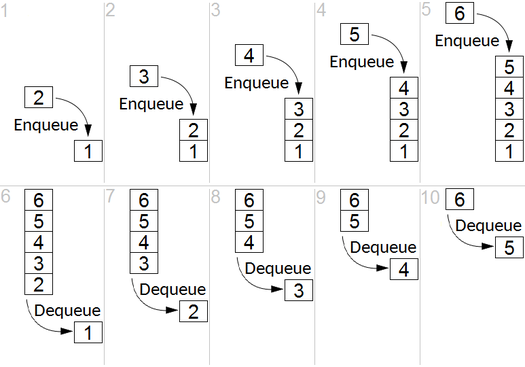
O BFS é usado para contar nós acessíveis a partir de um nó de origem em um gráfico não direcionado ou direcionado. Os nós acessíveis são impressos na ordem encontrada. Uma fila é usada para armazenar os nós de cor cinza (veja o GIF abaixo). O termo "largura" no BFS significa encontrar um nó acessível com o menor comprimento. A amplitude estende a fronteira entre os nós visitados e os nós não descobertos.
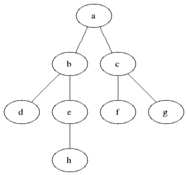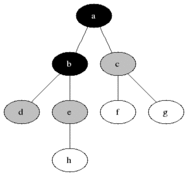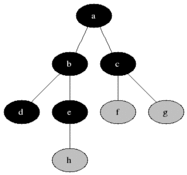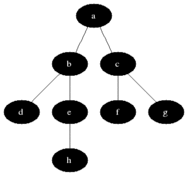
Propriedades
Back to Top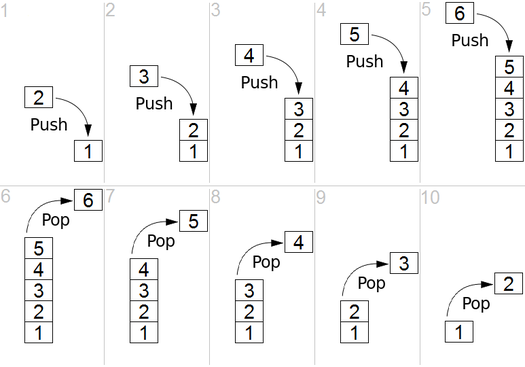
Ideia -chave
E o DFS é usado no gráfico direcionado e informa quantos nós um nó de origem pode alcançá -los e imprimi -los pelo pedido que os encontramos. Usamos a pilha para armazenar os nós classificamos como os pontos de partida para o gráfico. A "profundidade" em seu nome significa que esse algoritmo será o mais profundamente possível para uma determinada fonte e, quando atingir o terminal, ele retorna ao nó de início.
Propriedades
Back to Top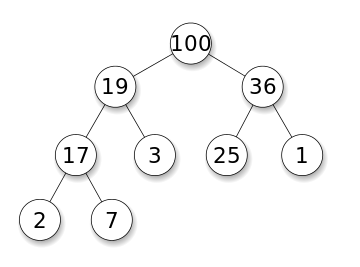
O problema médio de manutenção é que, se os números inteiros forem lidos a partir de um fluxo de dados, encontre a mediana dos elementos lidos assim para de maneira eficiente. Por simplicidade, assuma que não há duplicatas.
Ideia -chave
Podemos usar uma pilha máxima no lado esquerdo para representar elementos que são menos que a mediana eficaz e uma pilha min no lado direito para representar elementos maiores que a mediana eficaz. Quando a diferença entre o tamanho de dois pilhas é maior ou igual a 2, trocamos um elemento para outro pilheiro de tamanho menor.
Propriedades
Back to Top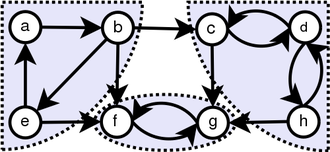
Ideia -chave
Através da simples observação, descobrimos que a transposição de gráficos tem os mesmos SCCs que o gráfico original. Nós executamos o DFS duas vezes. Primeira vez, o executamos no G e calculamos o tempo de acabamento para cada vértice. E então, executamos DFs em G^t, mas no loop principal do DFS, consideramos os vértices em ordem decrescente de tempo de acabamento.
Propriedades
Back to Top
Ideia -chave
Em um gráfico não direcionado, podemos usar essa estrutura de dados para descobrir quantos SCCs. A figura abaixo mostra como funciona.
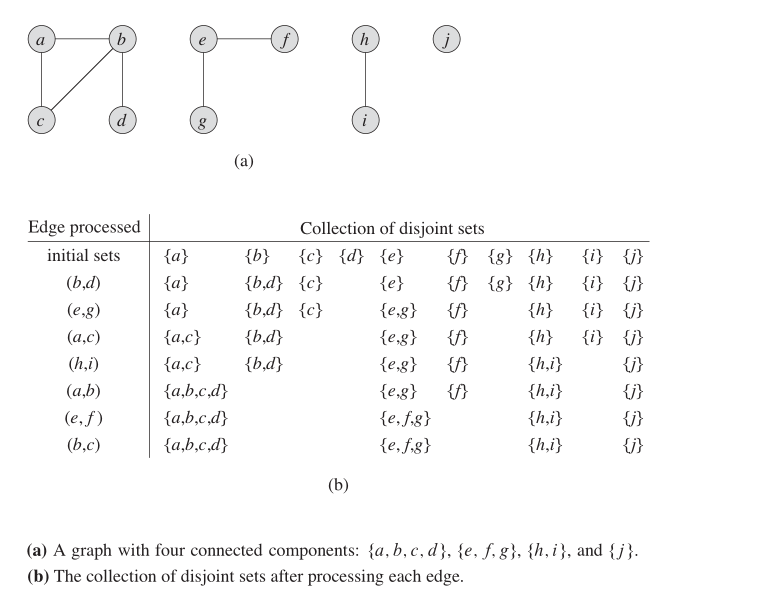
Propriedades
Back to Top Nesta seção, vou apresentar algoritmos gananciosos, uma poderosa estratégia de design de algoritmos.
Da Wikipedia, um algoritmo ganancioso é um paradigma algorítmico que segue o problema que resolve a heurística de fazer a escolha localmente ótima em cada estágio [1] com a esperança de encontrar um ótimo global. Em muitos problemas, uma estratégia gananciosa não produz, em geral, uma solução ideal, mas, no entanto, uma heurística gananciosa pode produzir soluções ideais localmente que se aproximam de uma solução ótima global em um tempo razoável.
No problema de seleção de atividades, toda atividade tem seu próprio peso e comprimento. E nosso objetivo é minimizar a soma do peso*comprimento. É um exemplo muito fácil e ótimo para mostrar como o algoritmo ganancioso funciona e fornecer uma prova elegante usando a técnica de troca de argumentos.
Ideia -chave
Se classificarmos a atividade por valor/comprimento, podemos provar que uma estrutura ideal existente não pode ser melhor que esse arranjo. 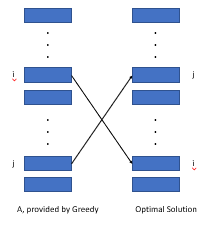
Como a figura mostrada acima, consideramos o custo causado por duas atividades que variam de maneira diferente em dois arranjos (i, j). Descobrimos que o custo no algoritmo ganancioso é menor que a estrutura ideal pelo valor de Wi*lj - WJ*li, que é maior ou igual a 0.
Propriedades
Back to Top
Ideia -chave
Nós classificamos a matriz de acordo com o horário de término. O algoritmo colocou o primeiro emprego cujo tempo de início é maior que o horário de término do último trabalho.
Propriedades
Back to Top
Uma maneira de codificar este livro é usar a codificação de comprimento fixo. Como mostrado abaixo:
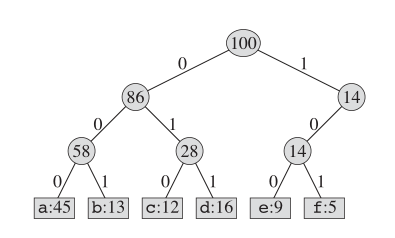
Quanto à codificação de Huffman, a estrutura real da árvore se parece com a seguinte:
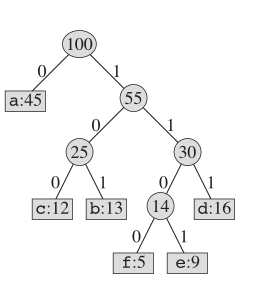
Ideia -chave
Mantemos uma árvore binária e criamos um novo nó como pai para duas letras menos frequentes. E a chave para esse novo nó é a soma das chaves para seus dois filhos. Repitamos isso até que não haja nós neste "livro".
Propriedades
Back to TopO algoritmo de Dijkstra é um algoritmo para encontrar os caminhos mais curtos entre nós em um gráfico. No entanto, tem um pré -requisito, todos os caminhos precisam ser maiores ou iguais a 0.
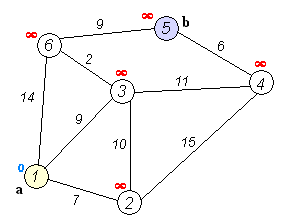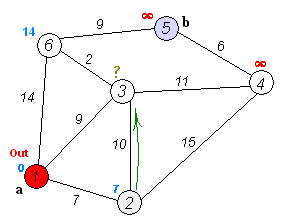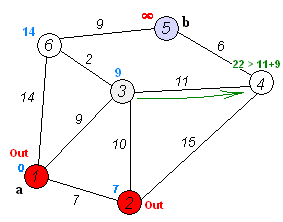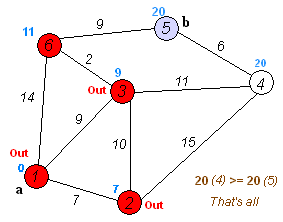
Ideia -chave
Nós separados em dois grupos, um grupo é marcado como explorado. E atualizamos a distância do grupo inexplorado para o grupo explorado pela menor distância.
Propriedades
Back to Top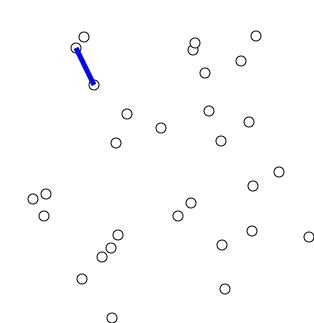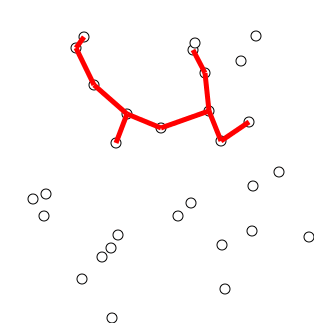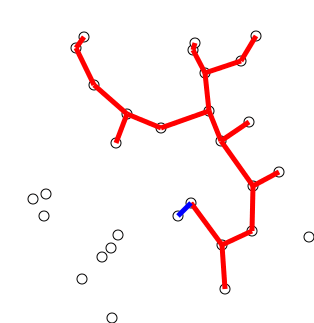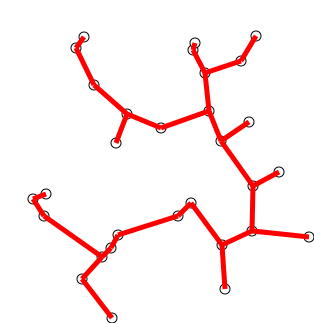
Ideia -chave
O algoritmo pode ser descrito informalmente como executando as seguintes etapas:
Inicialize uma árvore com um único vértice, escolhido arbitrariamente no gráfico.
Cultive a árvore por uma borda: das bordas que conectam a árvore a vértices ainda não na árvore, encontre a borda do peso mínimo e transfira-a para a árvore.
Repita a etapa 2 (até que todos os vértices estejam na árvore).
Propriedades
Back to Top
Ideia -chave
Muito semelhante ao SCC, podemos interromper mais cedo o alogritmo para controlar o número de classes em nosso gráfico, o que é dizer que podemos agrupar o gráfico.
Propriedades
Back to Top Nesta seção, vou introduzir algoritmos dinâmicos, uma poderosa estratégia de design de algoritmos.
Da Wikipedia, a programação dinâmica (também conhecida como otimização dinâmica) é um método para resolver um problema complexo, dividindo -o em uma coleção de subproblemas mais simples, resolvendo cada um desses subproblemas apenas uma vez e armazenando suas soluções.
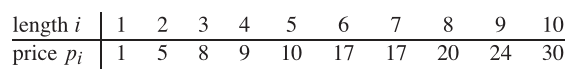
Portanto, se o comprimento da haste for 8 e os valores de peças diferentes forem dadas como seguintes, o valor máximo de obtenção é 22 (cortando dois pedaços de comprimentos 2 e 6).
Ideia -chave
Vemos uma decomposição como consistindo em um primeiro pedaço de comprimento, cortei a extremidade esquerda e, em seguida, um restante direito do comprimento n-i. Então, o pseudocódigo se parece:
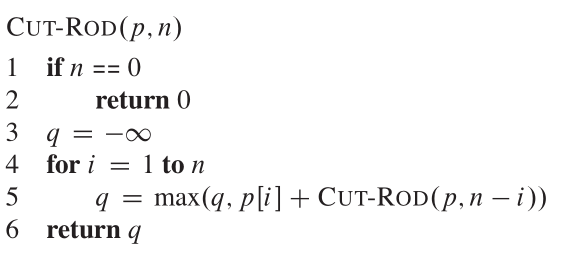
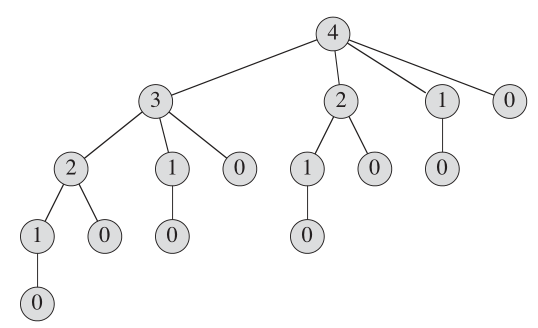
A árvore de recursão mostrando chamadas recursivas resultantes de uma chamada cut_rod (p, n) parece:
Para salvar o cálculo repetido para pequenos subproblemas, memorizamos uma matriz para armazenar esses valores.
Propriedades
Back to Top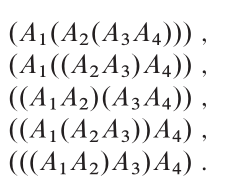
Ideia -chave
Estrutura ideal:
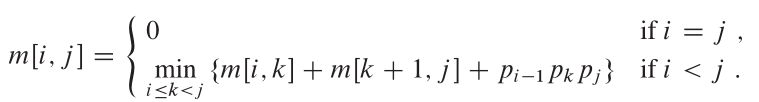
Propriedades
Back to Top Ideia -chave
No CLRS, a estrutura ideal para esse problema é:
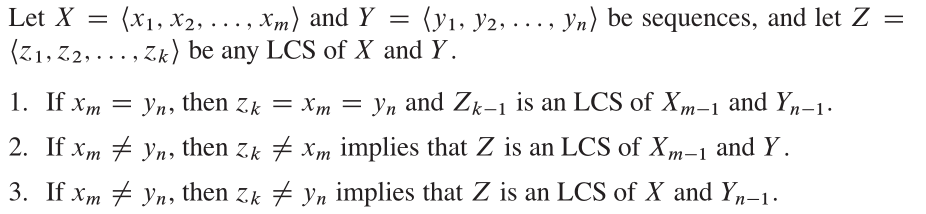
Propriedades
Back to Top Ideia -chave
Esse algoritmo é baseado em observação muito intuitiva. Suponha que tenhamos um subconjunto {1, 2, 3, 4, ..., k} (indicado como v (k)) do grupo original dos vértices {1, 2, 3, ..., n}. Se P é um caminho mais curto de I a J em V (k), temos dois casos. Primeiro, se K não estiver em P, então P deve ser um caminho mais curto em V (K-1). Segundo, se K estiver em P, então podemos separar o caminho em dois, p1: i K, P2: k j. e P1 deve ser o caminho mais curto de I a K com V (K-1), P2 deve ser o caminho mais curto de K a J com V (K-1).
Propriedades
Back to Top Da Wikipedia, um problema de decisão preenchido por NP é um pertencente às classes de complexidade NP e NP. Nesse contexto, o NP significa "tempo polinomial não determinístico". O conjunto de problemas de preenchimento NP é frequentemente indicado pelo NP-C ou NPC.
Nesta seção, vou apresentar três problemas muito famosos do NPC e explicar algoritmos de aproximação para abordá -los.
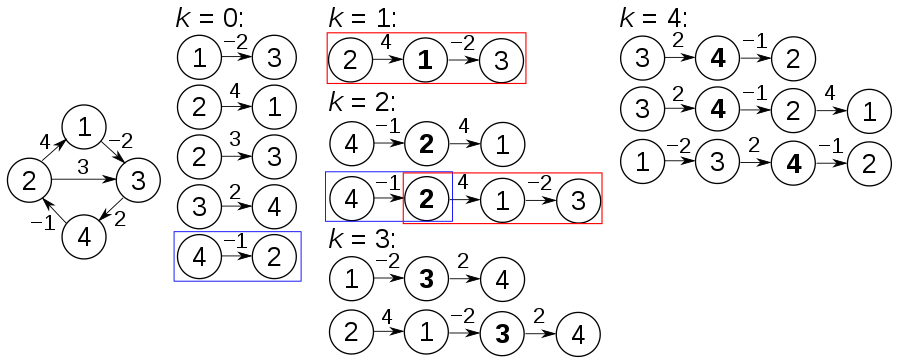
Ideia -chave
É muito difícil encontrar uma cobertura mínima de vértice, mas podemos encontrar uma cobertura aproximada com no máximo o dobro dos vértices no tempo polinomial.

Propriedades
Back to Top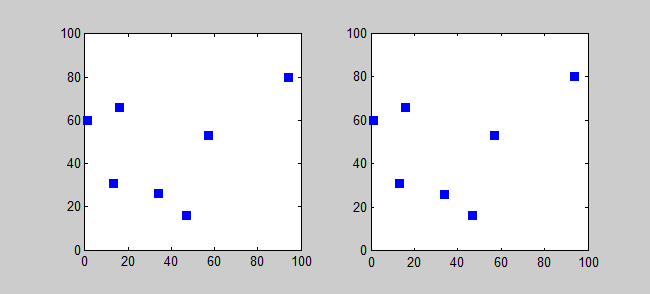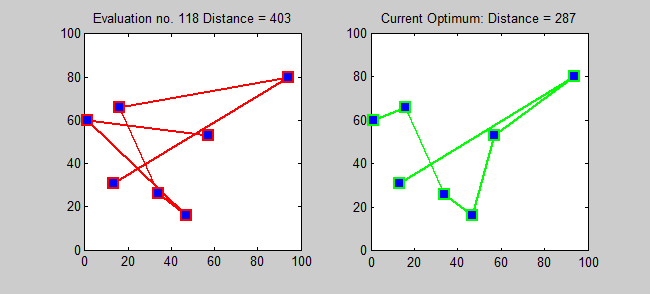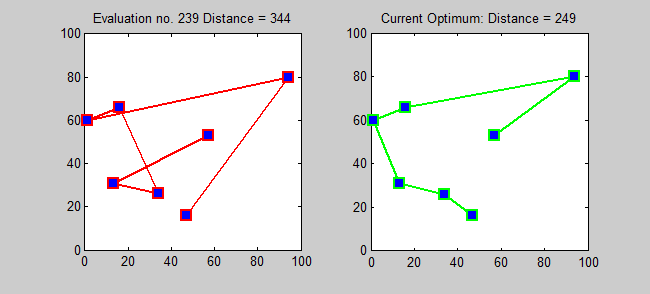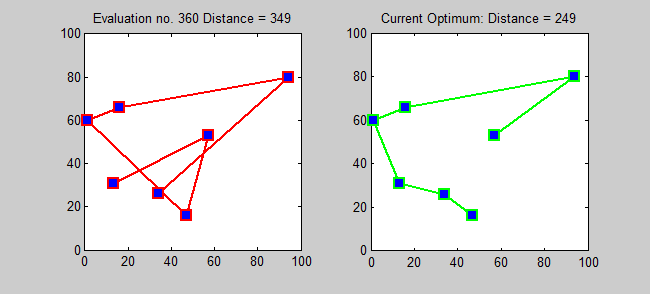
Ideia -chave
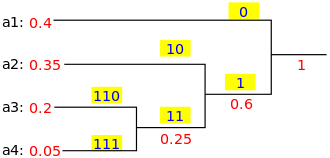
O algoritmo de aproximação para TSP é um algoritmo ganancioso (CLRS P1114). Aqui, também quero introduzir um algoritmo exato para TSP usando programação dinâmica.
Subproblema: Para todos os destinos j ∈ {1,2, ..., n}, todo subconjunto s ⊆ {1,2, ..., n} que contém 1 e j, deixe ls, j = comprimento mínimo de um caminho de 1 a j que visita precise dos vértices de s [uma vez cada]. Então, recorrência correspondente:
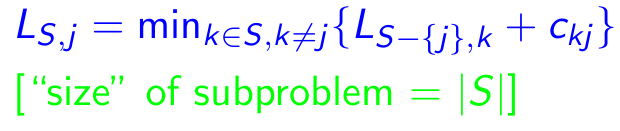
Propriedades
Back to Top O 3-SAT é um dos 21 problemas completos do KARP e é usado como ponto de partida para provar que outros problemas também são NP.
Aqui, apresento o algoritmo de Papadimitriou para 2-SAT (este é um algoritmo muito, muito interessante , então eu decido apresentá-lo, embora 2-SAT não seja NPC).
Ideia -chave
Escolha a atribuição inicial aleatória e escolha cláusula insatisfeita arbitrária e gire o valor de uma de sua variável. Aqui está o pseudocódigo:

Um lidar tão casual com cláusulas nos daria uma probabilidade muito grande de encontrar a resposta real. O mecanismo está em um termo de física (caminhada aleatória). Se você estiver interessado, recomendo fortemente que você passasse como caminhada aleatória relacionada a Papadimitriou.
Propriedades
Back to Top