algorithms in python

algoritma-in-python

Repositori ini, saya akan menggunakan Python untuk mengimplementasikan beberapa algoritma terkenal. Algoritma diatur sesuai dengan strategi yang digunakan. Setiap algoritma akan memiliki penjelasan tentang masalah yang dicoba diselesaikan dan beberapa sumber daya yang relevan.
(Tujuan dari repositori ini adalah untuk membuat readme yang indah untuk semua algoritma brilian yang telah saya ulas ini.)

Isi:

• 1.0 - Bagilah dan menaklukkan
  • 1.1 - Masalah multiplikasi interger
  • 1.2 - Gabungkan Sort (dan Sort Penyisipan)
  • 1.3 - Hitung inversi
  • 1.4 - Subarray maksimum
• 2.0 - Algoritma acak
  • 2.1 - Sortir Cepat
  • 2.2 - Algoritma Karger
• 3.0 - Struktur Data
  • 3.1 - Antrian dan Luas Pencarian Pertama
  • 3.2 - Tumpukan dan Kedalaman Pencarian Pertama
  • 3.3 - Tumpukan dan median median pemeliharaan
  • 3.4 - Komponen yang sangat terhubung
  • 3.5 - Disjoint -set dan SCC
• 4.0 - algoritma serakah
  • 4.1 - Kegiatan Shedule
  • 4.2 - Pemilihan Aktivitas
  • 4.3 - Huffman Coding
  • 4.4 - Algoritma Dijkstra
  • 4.5 - Algoritma Prim
  • 4.6 - Algoritma Kruskal dan masalah pengelompokan
• 5.0 - Pemrograman Dinamis
  • 5.1 - Pemotongan batang
  • 5.2 - Perkalian rantai matriks
  • 5.3 - Umum terpanjang setelahnya
  • 5.4 - Algoritma Floyd -Warshall
• 6.0 - Algoritma Perkiraan untuk NPC
  • 6.1 - Penutup Verteks
  • 6.2 - Masalah Salesman Bepergian
  • 6.3 - masalah kepuasan boolean

1.0 - Bagilah dan menaklukkan

Bagian ini, saya akan berbicara tentang strategi Divide and Conquer yang terkenal dan menunjukkan beberapa aplikasi dari strategi ini.

1.1 - Masalah multiplikasi interger

• Tautan yang berguna
  

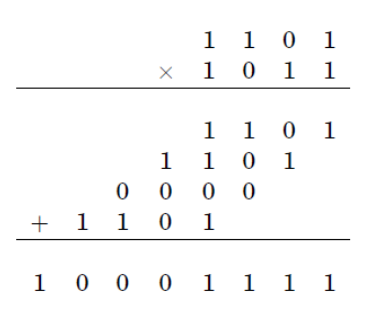
Prosedur standar untuk multiplikasi dua angka n digit membutuhkan sejumlah operasi dasar yang sebanding dengan. Adapun algoritma Karatsuba, ini mengurangi waktu berjalan ke sebagian besar

Ide utama
Langkah dasar algoritma Karatsuba adalah formula yang memungkinkan seseorang untuk menghitung produk dari dua angka besar dan menggunakan tiga multiplikasi angka yang lebih kecil, masing -masing dengan sekitar setengah lebih banyak digit atau, ditambah beberapa tambahan dan pergeseran digit.
Properti

• Waktu berjalan:
  Back to Top

1.2 - Gabungkan Sort (dan Sort Penyisipan)

• Tautan yang berguna
  Sebelum kita membahas gabungan gabungan, algoritma Sort Penyisipan akan dianalisis dan waktu berjalannya untuk menghargai jenis gabungan. Gambar di bawah ini menunjukkan ide intuitif untuk penyortiran adalah untuk meniru bagaimana kartu diatur sesuai dengan ukurannya. Ketika kami menerima kartu, kami segera mengaturnya berdasarkan kartu lain di tangan kami.

Waktu berjalan terburuk untuk algoritma ini adalah.
Gif di atas menunjukkan cara kerja gabungan bekerja:

Ide utama
Bagilah daftar yang tidak disortir ke dalam N sublists, masing -masing berisi 1 elemen (daftar elemen 1 dianggap diurutkan) dan berulang kali menggabungkan sublist untuk menghasilkan sublists baru yang diurutkan sampai hanya ada 1 sublist yang tersisa. Ini akan menjadi daftar yang diurutkan.
Properti

• Waktu berjalan:
  Back to Top

1.3 - Hitung inversi

• Tautan yang berguna
  Sebenarnya, ini dapat diperlakukan sebagai aplikasi jenis merger. Setiap kali kami melakukan operasi penggabungan dalam jenis gabungan, kami secara implisit menghitung inversi.
  

Ide utama
Seperti gambar di atas, ketika kita pertama kali menerima elemen dari sub-array kanan dalam operasi penggabungan, yang menunjukkan elemen kanan lebih kecil dari (panjang sub-array kiri-indeks elemen elemen kiri).
Saat algoritma berlangsung, tambahkan semua inversi akan memberi kita total inversi.
Properti

• Waktu berjalan:
  Back to Top

1.4 - Subarray maksimum

• Tautan yang berguna
  Masalah subarray maksimum adalah tugas menemukan subarray yang berdekatan dalam array satu dimensi, [1 ... n], dari jumlah yang memiliki jumlah terbesar.
  Ide utama
  Jika kita menggunakan strategi Divide and Conquer, jika array adalah [rendah .. Tinggi] dan titik tengah direpresentasikan sebagai pertengahan. A [i..j] adalah apa yang ingin kami hitung. A [i..j] harus menjadi salah satu dari tiga kasus:
  

• A [i..j] milik [rendah..mid]
• A [i..j] milik [mid+1..sebiganya]
• i <= mid <j
  Jadi, tugas kami adalah menemukan sub array terbesar melintasi titik tengah dan memilih yang terbesar di antara ketiga algoritma ini.

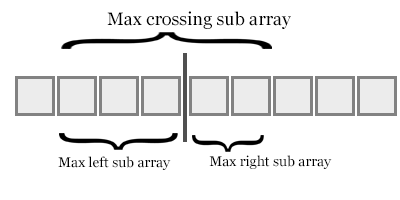
Properti

• Waktu berjalan:
  Back to Top

2.0 - Algoritma acak

Bagian ini saya akan berbicara tentang dua algoritma yang telah menggunakan variabel acak di dalamnya.

2.1 - Sortir Cepat

• Tautan yang berguna
  

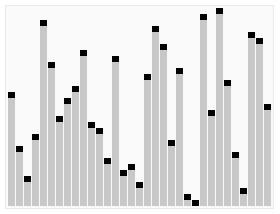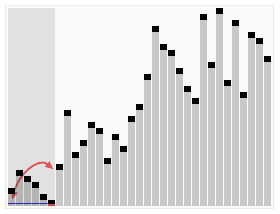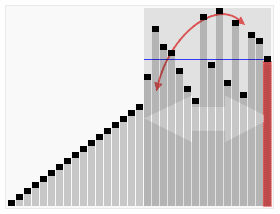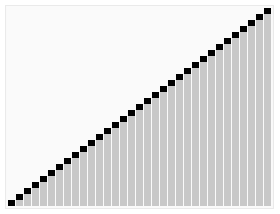
Ide utama
Quicksort pertama kali membagi array besar menjadi dua sub-array yang lebih kecil: elemen rendah dan elemen tinggi relatif terhadap elemen yang dipilih secara acak. Quicksort kemudian dapat mengurutkan sub-array secara rekursif. Jadi, titik kunci dalam jenis cepat adalah memilih elemen partisi.
Properti

• Kinerja kasus terburuk o (n^2)
• Kinerja kasus terbaik o (n log n) atau o (n) dengan partisi tiga arah
• Kinerja kasus rata -rata o (n log n)
  Back to Top

2.2 - Algoritma Karger

• Tautan yang berguna
  Gagasan algoritma didasarkan pada konsep kontraksi tepi (u, v) dalam grafik yang tidak diarahkan g = (v, e). Secara informal, kontraksi tepi menggabungkan node U dan V menjadi satu, mengurangi jumlah total node grafik dengan satu. Gambar di bawah ini menunjukkan cara kerja kontraksi. Di sub figur kiri, dua node hitam tebal menyatu menjadi satu (sub figur di kanan).

Ide utama
Dengan mengulangi waktu algoritma kontraksi dengan pilihan acak independen dan mengembalikan potongan terkecil, probabilitas tidak menemukan pemotongan minimum adalah
Properti

• Dengan probabilitas tinggi kita dapat menemukan semua pemotongan min dalam waktu berjalan
• Tidak menemukan probabilitas pemotongan min adalah waktu.
  Back to Top

3.0 - Struktur Data

Untuk menempatkan struktur data sebagai bagian independen menyesatkan; Namun, saya akan memperkenalkan masalah yang membingungkan yang diselesaikan secara elegan oleh struktur data. Beberapa struktur data mungkin memiliki strategi desain algoritma yang belum ditinjau.

3.1 - Antrian dan Luas Pencarian Pertama

• Link1 Link2 yang berguna
  Antrian, juga dikenal sebagai FIFO, adalah akronim untuk First In, First Out, metode untuk mengatur dan memanipulasi buffer data, di mana entri tertua (pertama), atau 'kepala' antrian, diproses terlebih dahulu.

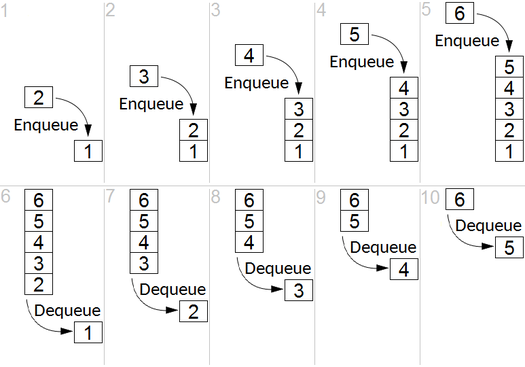
Ide utama
BFS digunakan untuk menghitung node yang dapat dijangkau dari node sumber dalam grafik yang tidak terarah atau diarahkan. Node yang dapat dijangkau dicetak dalam urutan yang ditemukan. Antrian digunakan untuk menyimpan node berwarna abu -abu (lihat gif di bawah). Istilah "luas" di BFS berarti menemukan simpul yang dapat dijangkau dengan panjang terpendek. Luasnya memperluas perbatasan antara node yang dikunjungi dan node yang belum ditemukan.

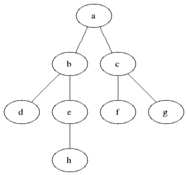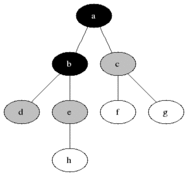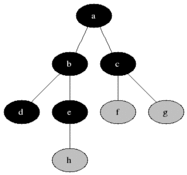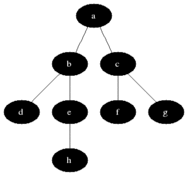
Properti

• Waktu berjalan: t (n) = o (v+e), v adalah jumlah simpul, e adalah jumlah tepi
  Back to Top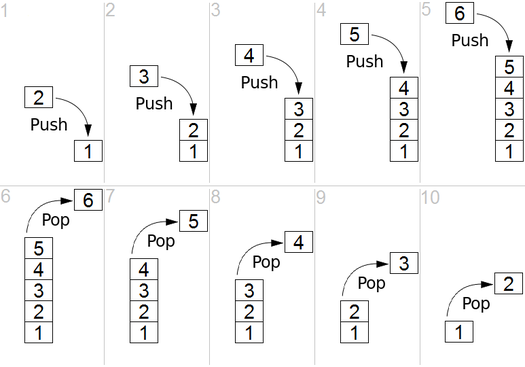

3.2 - Tumpukan dan Kedalaman Pencarian Pertama

• Link1 Link2 yang berguna
  Stack, juga dikenal sebagai Lifo, memiliki properti terakhir, pertama keluar.
  

Ide utama
Dan DFS digunakan dalam grafik terarah dan memberi tahu berapa banyak node yang dapat dijangkau oleh simpul sumber dan mencetaknya dengan urutan yang kami temukan. Kami menggunakan Stack untuk menyimpan node yang kami klasifikasi sebagai titik awal untuk grafik. "Kedalaman" dalam namanya berarti bahwa algoritma ini akan berjalan sedalam mungkin untuk sumber yang diberikan dan ketika mencapai titik akhir, ia kembali ke simpul start.

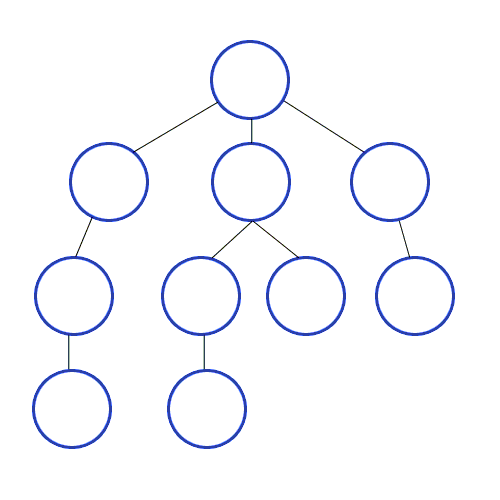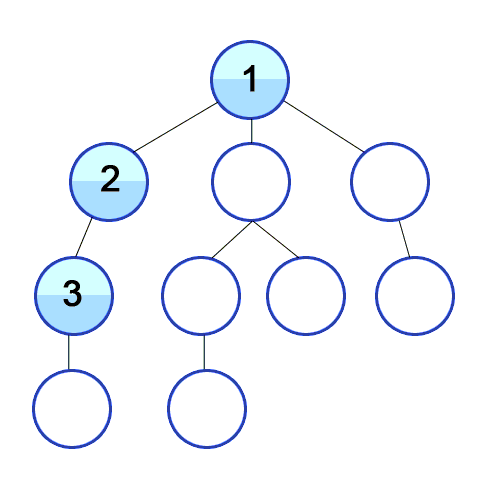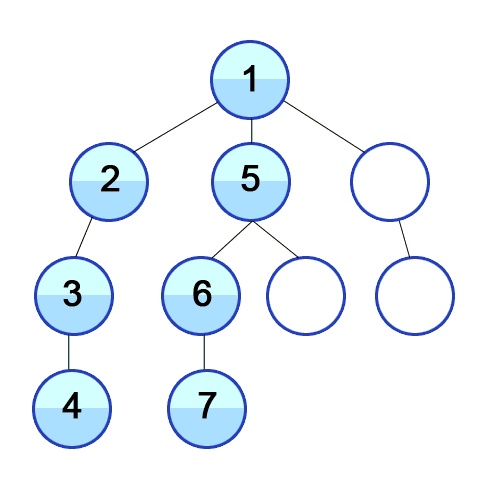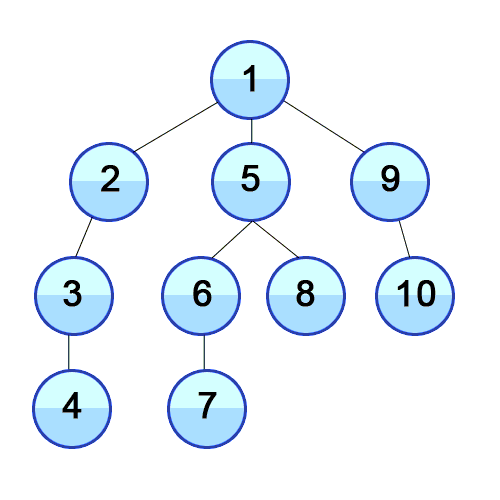
Properti

• Waktu berjalan: t (n) = o (v+e), v adalah jumlah simpul, e adalah jumlah tepi
  Back to Top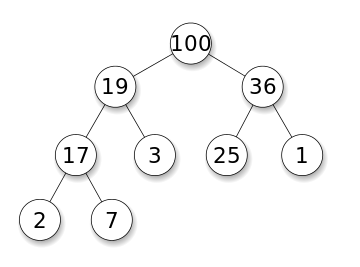

3.3 - Tumpukan dan median median pemeliharaan

• Link1 Link2 yang berguna
  Heap adalah struktur data berbasis pohon khusus yang memenuhi properti heap: jika p adalah simpul induk C, maka kunci (nilai) p lebih besar dari atau sama dengan (dalam tumpukan maks) atau kurang dari atau sama dengan (dalam heap min) kunci C. [1] Node di "atas" tumpukan (tanpa orang tua) disebut simpul root.

Masalah pemeliharaan median adalah bahwa jika bilangan bulat dibaca dari aliran data, temukan median elemen yang dibaca demikian dengan cara yang efisien. Untuk kesederhanaan, anggap tidak ada duplikat.

Ide utama
Kita dapat menggunakan tumpukan maks di sisi kiri untuk mewakili elemen yang kurang dari median yang kurang efektif, dan tumpukan min di sisi kanan untuk mewakili elemen yang lebih besar dari median efektif. Ketika perbedaan antara ukuran dua tumpukan lebih besar atau sama dengan 2, kami beralih satu elemen ke tumpukan ukuran lain yang lebih kecil.

Properti

• Waktu berjalan:
  Back to Top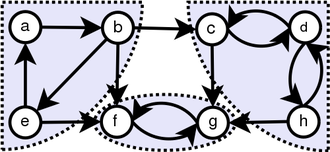

3.4 - Komponen yang sangat terhubung

• Tautan yang berguna
  Grafik terarah disebut sangat terhubung jika ada jalur di setiap arah antara setiap pasangan simpul grafik. Dalam grafik terir yang mungkin tidak terhubung dengan kuat, sepasang simpul U dan V dikatakan sangat terhubung satu sama lain jika ada jalur di setiap arah di antara mereka.

Ide utama
Melalui pengamatan sederhana, kami mengetahui bahwa tranpose grafik memiliki SCC yang sama dengan grafik asli. Kami menjalankan DFS dua kali. Pertama kali, kami menjalankannya pada G dan menghitung waktu finishing untuk setiap simpul. Dan kemudian, kita menjalankan DFS pada g^t tetapi di loop utama DFS, pertimbangkan simpul dalam urutan penurunan waktu finishing.
Properti

• Waktu berjalan :, v adalah jumlah simpul, E adalah jumlah tepi
  Back to Top

3.5 - Disjoint -set dan SCC

• Tautan yang berguna
  Struktur data yang dipisahkan, yang juga disebut struktur data penembak serikat atau himpunan gabungan, adalah struktur data yang melacak serangkaian elemen yang dipartisi ke dalam sejumlah himpunan bagian (tidak tumpang tindih).
  Untuk set terputus-putus yang naif, ini mendukung dua operasi utama, make-set dan Union. Make-set membuat setiap simpul grup independen. Union menempatkan dua simpul dalam satu kelompok.

Ide utama
Dalam grafik yang tidak diarahkan, kita dapat menggunakan struktur data ini untuk mengetahui berapa banyak SCC. Gambar di bawah ini menunjukkan cara kerjanya.

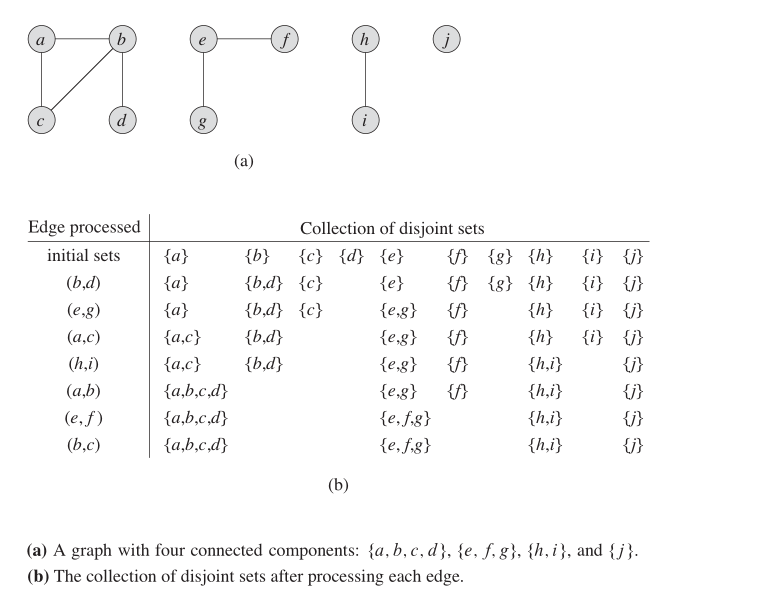
Properti

• Kita dapat menggunakan heuristik serikat tertimbang untuk menghemat waktu saat panggilan find_set
• Kompresi jalur dapat sangat meningkatkan efisiensi waktu penemuan serikat pekerja
  Back to Top

4.0 - algoritma serakah

Di bagian ini, saya akan memperkenalkan algoritma serakah, satu strategi desain algoritma yang kuat.
Dari Wikipedia, algoritma serakah adalah paradigma algoritmik yang mengikuti heuristik pemecahan masalah dalam membuat pilihan optimal lokal pada setiap tahap [1] dengan harapan menemukan optimal global. Dalam banyak masalah, strategi serakah tidak secara umum menghasilkan solusi yang optimal, tetapi tetap saja heuristik serakah dapat menghasilkan solusi optimal lokal yang mendekati solusi optimal global dalam waktu yang wajar.

4.1 - Kegiatan Shedule

Dalam masalah pemilihan aktivitas, setiap aktivitas memiliki berat dan panjangnya sendiri. Dan tujuan kami adalah untuk meminimalkan jumlah berat*. Ini adalah contoh yang sangat mudah dan bagus untuk menunjukkan bagaimana algoritma serakah bekerja dan memberikan bukti yang elegan menggunakan teknik pertukaran argumen.
Ide utama
Jika kita mengurutkan aktivitas berdasarkan berat/panjang nilai, kita dapat membuktikan struktur optimal yang ada tidak bisa lebih baik dari pengaturan ini.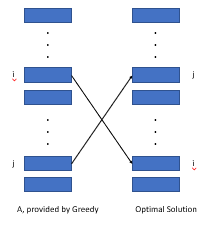

Seperti gambar yang ditunjukkan di atas, kami mempertimbangkan biaya yang disebabkan oleh dua kegiatan yang berkisar berbeda dalam dua pengaturan (I, J). Kami mengetahui bahwa biaya dalam algoritma serakah lebih kecil dari struktur optimal dengan nilai wi*lj - wj*li, yang lebih besar dari atau sama dengan 0.

Properti

• Waktu berjalan didominasi oleh penyortiran
  Back to Top

4.2 - Pemilihan Aktivitas

• Tautan yang berguna
  Dalam masalah ini, setiap kegiatan memiliki waktu mulai dan akhir waktu. Tujuan kami adalah memilih subset max-length, di mana pekerjaan kompatibel.
  

Ide utama
Kami mengurutkan array sesuai dengan waktu selesai. Algoritma ini menempatkan pekerjaan pertama yang waktu mulainya lebih besar dari waktu selesai Last Job.
Properti

• Waktu berjalan seleksi aktivitas rekursif adalah
  Back to Top

4.3 - Huffman Coding

• Tautan yang berguna
  Huffman Code adalah jenis kode awalan optimal tertentu yang biasanya digunakan untuk kompresi data lossless. Misalnya, tabel di bawah ini menunjukkan frekuensi huruf dalam "buku".

Salah satu cara untuk menyandikan buku ini adalah dengan menggunakan pengkodean panjang tetap. Seperti yang ditunjukkan di bawah ini:

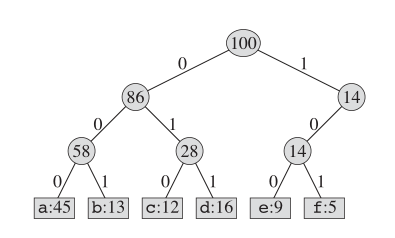
Adapun pengkodean Huffman, struktur pohon yang sebenarnya terlihat seperti ini:

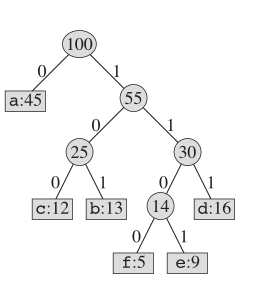
Ide utama
Kami memelihara pohon biner dan membuat simpul baru sebagai induk untuk dua huruf yang paling tidak sering. Dan kunci untuk simpul baru ini adalah jumlah kunci untuk kedua anaknya. Kami mengulangi ini sampai tidak ada node yang tersisa di "buku" ini.

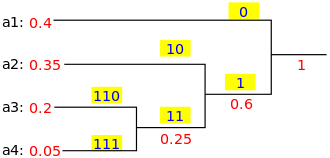
Properti

• Prosedur Huffman menghasilkan kode awalan yang optimal
  Back to Top

4.4 - Algoritma Dijkstra

• Tautan yang berguna
  

Algoritma Dijkstra adalah algoritma untuk menemukan jalur terpendek antara node dalam grafik. Namun, ia memiliki satu prasyarat, semua jalur harus lebih besar atau sama dengan 0.

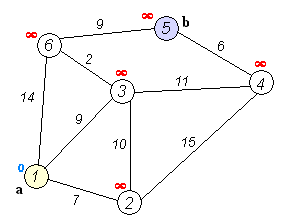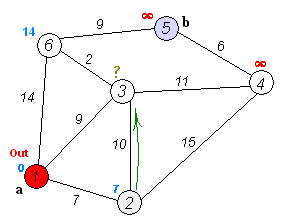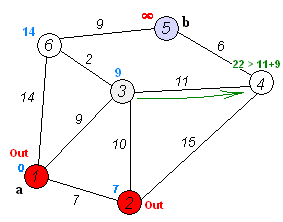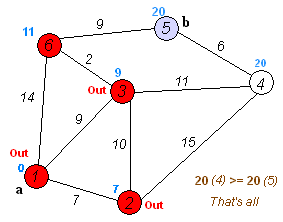
Ide utama
Node terpisah menjadi dua kelompok, satu kelompok ditandai seperti yang dieksplorasi. Dan kami memperbarui jarak dari grup yang belum dijelajahi ke grup yang dijelajahi dengan jarak terpendek.

Properti

• Waktu berjalan berdasarkan antrian prioritas min yang diimplementasikan oleh heap fibonacci
  Back to Top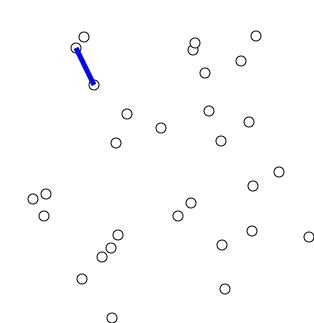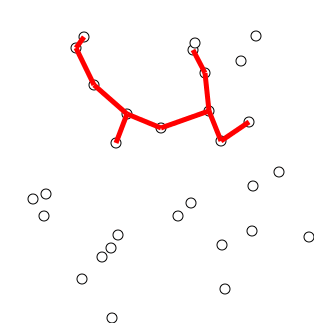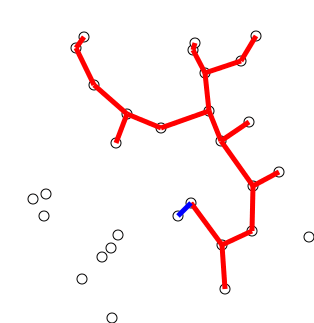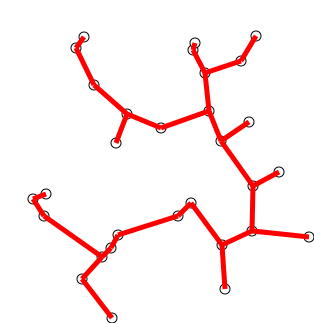

4.5 - Algoritma Prim

• Tautan yang berguna
  Algoritma Prim adalah algoritma serakah yang menemukan pohon spanning minimum untuk grafik yang tidak tertimbang. Sangat mirip dengan algoritma Dijkstra, kami mempertahankan dua set, menjelajahi satu dan satu yang belum dijelajahi. Setiap kali, kami hanya menyerap simpul, yang memiliki jarak terkecil untuk dieksplorasi. Ini ditunjukkan dengan sangat jelas pada gambar di bawah ini:

Ide utama
Algoritma dapat secara informal digambarkan sebagai melakukan langkah -langkah berikut:

Inisialisasi pohon dengan satu titik, dipilih secara sewenang -wenang dari grafik.
Tumbuhkan pohon dengan satu tepi: dari tepi yang menghubungkan pohon ke simpul belum di pohon, temukan tepi minimum, dan pindahkan ke pohon.
Ulangi Langkah 2 (sampai semua simpul ada di pohon).

Properti

• Waktu berjalan

• Matriks kedekatan, pencarian
• Daftar tumpukan biner dan kedekatan
• Daftar Tumpukan dan kedekatan Fibonacci
  Back to Top

4.6 - Algoritma Kruskal dan masalah pengelompokan

• Tautan yang berguna
  Algoritma Prim adalah algoritma serakah lain yang menemukan pohon spanning minimum untuk grafik tidak terarah yang tidak tertimbang. Alih -alih memelihara pohon seperti prim, ia mempertahankan hutan.

Ide utama
Sangat mirip dengan SCC, kita dapat menghentikan alogrithm awal untuk mengontrol jumlah kelas dalam grafik kita, yang berarti kita dapat mengelompokkan grafik.

Properti

• Waktu berjalan o (elogv)
  Back to Top

5.0 - Pemrograman Dinamis

Di bagian ini, saya akan memperkenalkan algoritma dinamis, satu strategi desain algoritma yang kuat.
Dari Wikipedia, pemrograman dinamis (juga dikenal sebagai Optimasi Dinamis) adalah metode untuk menyelesaikan masalah yang kompleks dengan memecahnya menjadi kumpulan subproblem yang lebih sederhana, memecahkan masing -masing subproblem tersebut hanya sekali, dan menyimpan solusi mereka.

5.1 - Pemotongan batang

• Tautan yang berguna
  Diberi batang panjang N inci dan serangkaian harga yang berisi harga semua ukuran lebih kecil dari n. Tentukan nilai maksimum yang dapat diperoleh dengan memotong batang dan menjual potongan.
  Tabel berikut menunjukkan hubungan antara harga dan panjang.

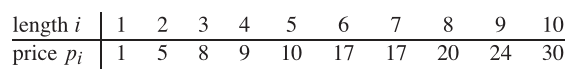
Jadi, jika panjang batang adalah 8 dan nilai -nilai potongan yang berbeda diberikan sebagai berikut, maka nilai maksimum yang dapat diperoleh adalah 22 (dengan memotong dua potong panjang 2 dan 6).

Ide utama
Kami melihat dekomposisi sebagai terdiri dari sepotong panjang pertama saya memotong ujung kiri, dan kemudian sisa tangan kanan panjang n-i. Jadi, pseudocode terlihat seperti:

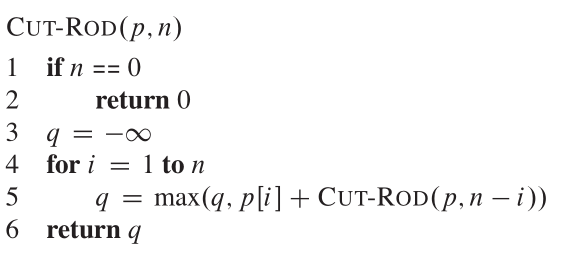
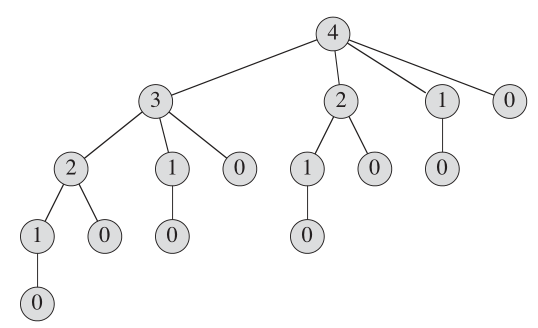
Pohon rekursi yang menunjukkan panggilan rekursif yang dihasilkan dari panggilan cut_rod (p, n) terlihat seperti:

Untuk menyimpan perhitungan berulang untuk sub-masalah kecil, kami menghafal array untuk menyimpan nilai-nilai ini.

Properti

• Kompleksitas waktu implementasi di atas adalah O (n^2)
  Back to Top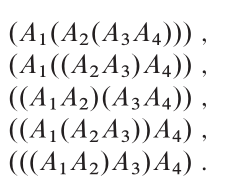

5.2 - Perkalian rantai matriks

• Tautan yang berguna
  Multiplikasi rantai matriks (atau masalah pemesanan rantai matriks, MCOP) adalah masalah optimisasi yang dapat diselesaikan dengan menggunakan pemrograman dinamis. Diberi urutan matriks, tujuannya adalah untuk menemukan cara paling efisien untuk melipatgandakan matriks ini. Masalahnya sebenarnya bukan untuk melakukan perkalian, tetapi hanya untuk memutuskan urutan multiplikasi matriks yang terlibat.

Ide utama
Struktur optimal:

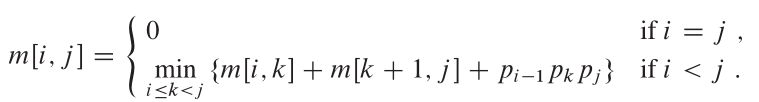
Properti

• Kompleksitas waktu implementasi di atas adalah
  Back to Top

5.3 - Umum terpanjang setelahnya

• Tautan yang berguna
  Masalah Common Common (LCS) terpanjang adalah masalah menemukan yang paling lama umum untuk semua sekuens dalam serangkaian urutan (seringkali hanya dua urutan).

Ide utama
Dari CLRS, struktur optimal untuk masalah ini adalah:

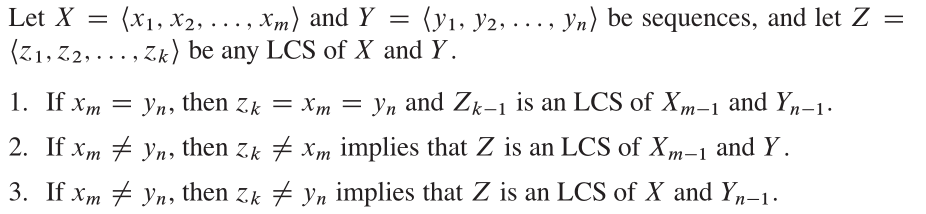
Properti

• Kompleksitas waktu implementasi di atas adalah $ theta (mn) $
  Back to Top

5.4 - Algoritma Floyd -Warshall

• Tautan yang berguna
  Algoritma Floyd -Warshall adalah algoritma untuk menemukan jalur terpendek dalam grafik tertimbang dengan bobot tepi positif atau negatif (tetapi tanpa siklus negatif).

Ide utama
Algoritma ini didasarkan pada pengamatan yang sangat intuitif. Misalkan kita memiliki subset {1, 2, 3, 4, ..., k} (menunjukkan sebagai v (k)) dari kelompok simpul asli {1, 2, 3, ..., n}. Jika P adalah jalan terpendek dari I ke J dalam V (k), kami memiliki dua kasus. Pertama, jika k tidak ada di P, maka P harus menjadi jalur terpendek di V (K-1). Kedua, jika k ada di P, maka kita dapat memisahkan jalan menjadi dua, p1: i K, P2: k J. dan P1 harus menjadi jalan terpendek dari I ke K dengan V (K-1), P2 harus menjadi jalan terpendek dari K ke J dengan V (K-1).

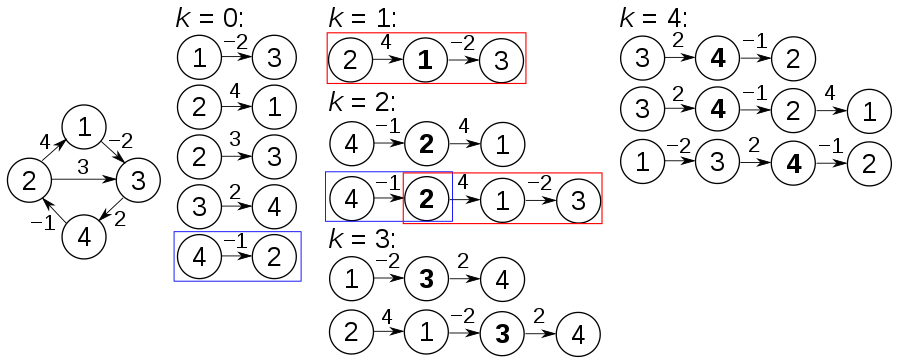
Properti

• Kompleksitas waktu implementasi di atas adalah
  Back to Top

6.0 - Algoritma Perkiraan untuk NPC

Dari dari Wikipedia, masalah keputusan NP-lengkap adalah salah satu milik NP dan kelas kompleksitas NP-hard. Dalam konteks ini, NP berarti "waktu polinomial nondeterministik". Set masalah NP-Complete sering dilambangkan dengan NP-C atau NPC.

Di bagian ini, saya akan memperkenalkan tiga masalah NPC yang sangat terkenal dan menjelaskan algoritma perkiraan untuk mendekatinya.

6.1 - Penutup Verteks

• Tautan yang berguna
  Penutup simpul (kadang -kadang penutup simpul) dari grafik adalah satu set simpul sehingga setiap tepi grafik adalah insiden untuk setidaknya satu simpul dari set. Gambar di bawah ini menunjukkan penutup verteks minimum (di mana set penutup harus memiliki setidaknya dua simpul, nol dan satu tidak akan membantu).

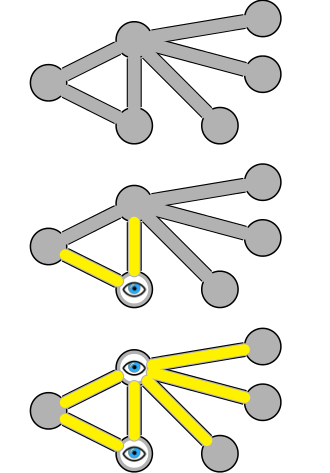
Ide utama
Sangat sulit untuk menemukan penutup simpul minimum tetapi kita dapat menemukan penutup perkiraan dengan paling banyak dua kali simpul dalam waktu polinomial.

Properti

• Appror-Vertex-Cover adalah algoritma 2-aproksimasi waktu polinomial.
  Back to Top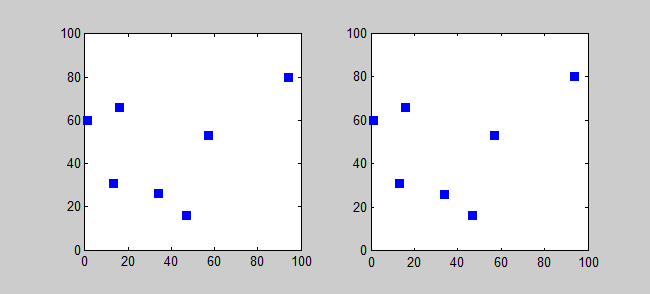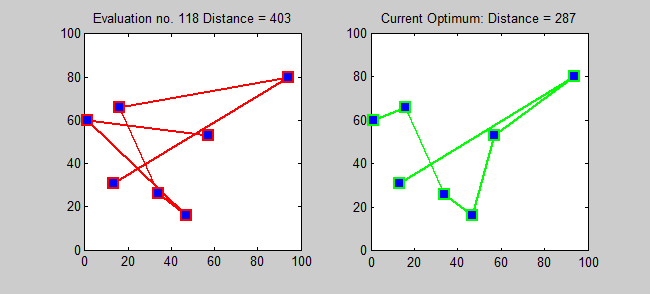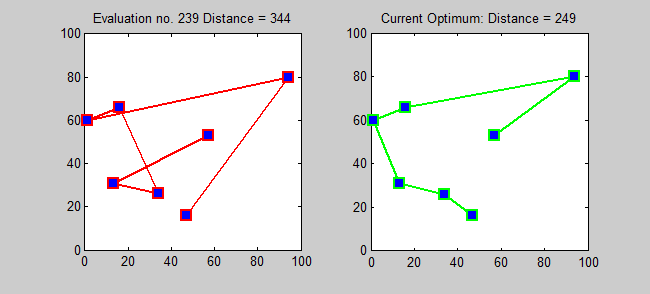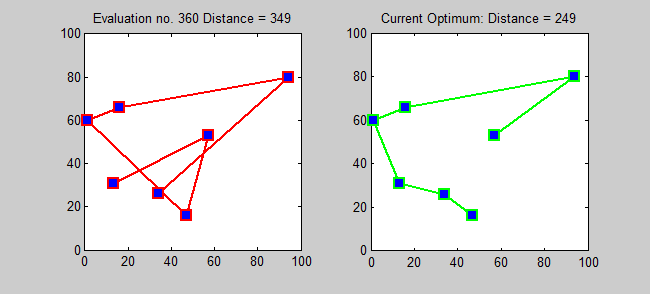

6.2 - Masalah Salesman Bepergian

• Tautan yang berguna
  The Travelling Salesman Problem (TSP) mengajukan pertanyaan berikut: "Diberikan daftar kota dan jarak antara setiap pasangan kota, apa rute sesingkat mungkin yang mengunjungi setiap kota dan kembali ke kota asal?" GIF menunjukkan kekuatan kasar untuk TSP.

Ide utama
Algoritma perkiraan untuk TSP adalah algoritma serakah (CLRS P1114). Di sini, saya juga ingin memperkenalkan algoritma yang tepat untuk TSP menggunakan pemrograman dinamis.

Subproblem: Untuk setiap tujuan j ∈ {1,2, ..., n}, setiap subset s {1,2, ..., n} yang berisi 1 dan j, mari ls, j = panjang minimum jalur dari 1 ke j yang mengunjungi tepatnya simpul s [tepat sekali masing -masing]. Jadi, kekambuhan yang sesuai:

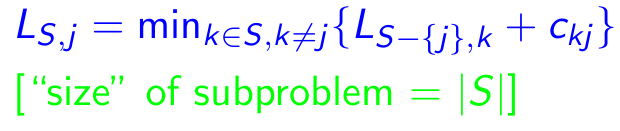
Properti

• Waktu berjalan untuk algoritma yang tepat:
  Back to Top

6.3 - masalah kepuasan boolean

• Tautan yang berguna
  Masalah kepuasan boolean (kadang -kadang disebut masalah kepuasan proposisional dan disingkat kepuasan atau SAT) adalah masalah menentukan apakah ada interpretasi yang memenuhi formula boolean yang diberikan.

3-SAT adalah salah satu dari 21 masalah lengkap NP-NP, dan digunakan sebagai titik awal untuk membuktikan bahwa masalah lain juga keras.

Di sini, saya memperkenalkan algoritma Papadimitriou untuk 2-SAT (ini adalah algoritma yang sangat sangat menarik , jadi saya memutuskan untuk memperkenalkannya meskipun 2-SAT bukan NPC).

Ide utama
Pilih penugasan awal acak dan pilih klausa yang tidak puas sewenang -wenang dan balikkan nilai salah satu variabelnya. Ini pseudocode:

Kesepakatan santai seperti itu dengan klausa akan secara mengejutkan memberi kita kemungkinan yang sangat besar untuk menemukan jawaban yang sebenarnya. Mekanisme ini terletak pada istilah fisika (jalan acak). Jika Anda tertarik, saya sangat menyarankan Anda untuk melalui bagaimana berjalan acak terkait dengan papadimitriou.

Properti

• Untuk instance 2-SAT yang memuaskan dengan variabel N, algoritma papadimitriou menghasilkan penugasan yang memuaskan dengan probabilitas ≥ 1-1/n
• Berjalan dalam waktu polinomial
• Selalu perbaiki pada contoh yang tidak memuaskan
  Back to Top