algorithms in python

Алгоритмы-в питоне

В этом хранилище я буду использовать Python для реализации некоторых известных алгоритмов. Алгоритмы расположены в соответствии с используемой стратегией. Каждый алгоритм будет иметь объяснение проблемы, которую она пытается решить, и некоторые соответствующие ресурсы.
(Цель этого репозитория - создать прекрасную Readme для всех этих блестящих алгоритмов, которые я рассмотрел.)

Содержание:

• 1.0 - разделите и побеждайте
  • 1.1 - Проблема размножения интеркала
  • 1.2 - сортировка слияния (и вставка)
  • 1.3 - Считайте инверсии
  • 1.4 - максимальный субрай
• 2.0 - рандомизированные алгоритмы
  • 2.1 - быстрая сортировка
  • 2.2 - Алгоритм Каргера
• 3.0 - Структуры данных
  • 3.1 - Первый поиск в очереди и ширине
  • 3.2 - стек и глубина первого поиска
  • 3.3 - Куча и медианное обслуживание
  • 3.4 - сильно связанный компонент
  • 3.5 - Discoint -Set и SCC
• 4.0 - жадные алгоритмы
  • 4.1 -
  • 4.2 - Выбор активности
  • 4.3 - Кодирование Хаффмана
  • 4.4 - Алгоритм Дейкстры
  • 4.5 - Алгоритм Прима
  • 4.6 - Алгоритм и проблема кластеризации Крускала
• 5.0 - Динамическое программирование
  • 5.1 - Резка стержня
  • 5.2 - умножение матричной цепи
  • 5.3 - Самая длинная общая последующая последовательность
  • 5.4 - Алгоритм Флойд -Варшалла
• 6.0 - Алгоритмы приближения для NPC
  • 6.1 - крышка вершины
  • 6.2 - Проблема с продавцом -путешественниками
  • 6.3 - Проблема логической удовлетворенности

1.0 - разделите и побеждайте

В этом разделе я расскажу о знаменитой стратегии «Разделение и победит» и покажу некоторые приложения этой стратегии.

1.1 - Проблема размножения интеркала

• Полезная ссылка
  

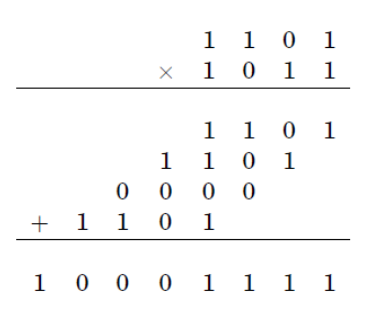
Стандартная процедура для умножения двух N-цифр требует ряд элементарных операций, пропорциональных. Что касается алгоритма карацуба, он уменьшает время работы до максимума

Ключевая идея
Основным шагом алгоритма Карацубы является формула, которая позволяет вычислять продукт двух больших чисел и использовать три умножения меньших чисел, каждая из которых составляет около половины цифр, а также, плюс некоторые дополнения и цифровые сдвиги.
Характеристики

• Время работы:
  Back to Top

1.2 - сортировка слияния (и вставка)

• Полезная ссылка
  Прежде чем мы обсудим сортировку слияния, будет проанализирован алгоритм сортировки вставки, и его время работы с целью оценить сортировку слияния. На рисунке ниже показана интуитивная идея сортировки, чтобы имитировать, как карты расположены в соответствии с его размером. Когда мы получаем карту, мы сразу же организуем ее на основе других карт в нашей руке.

Худшее время для этого алгоритма - это.
GIF выше показывает, как работает сортировка слияния:

Ключевая идея
Разделите несортированный список на N -сублисты, каждый из которых содержит 1 элемент (список из 1 элемента считается отсортированным) и неоднократно объединяет сублисты для создания новых отсортированных сублистов, пока остается только 1 сублисты. Это будет отсортированный список.
Характеристики

• Время работы:
  Back to Top

1.3 - Считайте инверсии

• Полезная ссылка
  На самом деле, это можно рассматривать как применение сортировки слияния. Каждый раз, когда мы выполняем операцию слияния в сортировке слияния, мы неявно рассчитываем инверсии.
  

Ключевая идея
Как и рисунок выше, когда мы впервые принимаем элемент с правой подоружкой в ​​операции слияния, что указывает на то, что правый элемент меньше (длина левой подрайки-индекс левого элемента) элементов.
По мере развития алгоритма добавить все инверсии даст нам общие инверсии.
Характеристики

• Время работы:
  Back to Top

1.4 - максимальный субрай

• Полезная ссылка
  Максимальная проблема Subarray-задача поиска смежного субрайя в одномерном массиве, a [1 ... n] чисел, которые имеют наибольшую сумму.
  Ключевая идея
  Если мы используем стратегию разделения и завоевания, если массив является [низким ... высоким], а средняя точка представлена ​​как средняя. [I..j] - это то, что мы хотим рассчитать. [I..J] должен быть одним из трех случаев:
  

• [I..j] принадлежит [низко .. мимо]
• [I..J] принадлежит [середине+1..high]
• я <= середина <j
  Таким образом, наша задача - найти самый большой подметок, пересекающий среднюю точку и выбрать самый большой среди этих трех алгоритмов.

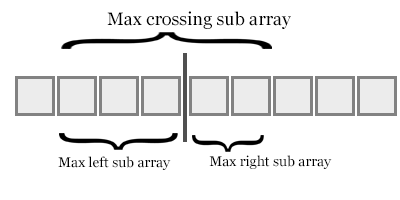
Характеристики

• Время работы:
  Back to Top

2.0 - рандомизированные алгоритмы

В этом разделе я расскажу о двух алгоритмах, которые использовали случайную величину внутри.

2.1 - быстрая сортировка

• Полезная ссылка
  

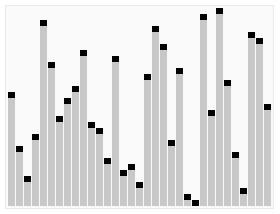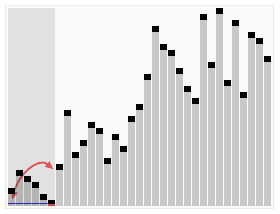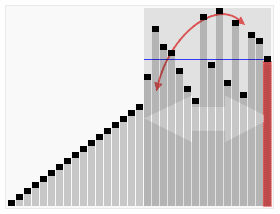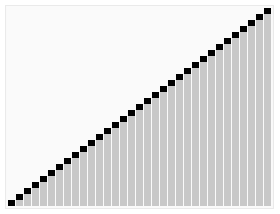
Ключевая идея
QuickSort сначала делит большой массив на две меньшие суб-борьбы: низкие элементы и высокие элементы относительно случайно выбранного элемента. QuickSort может затем рекурсивно сортировать суб-магистрали. Таким образом, ключевым моментом в быстром сортировке является выбор элемента раздела.
Характеристики

• Худший случай производительности o (n^2)
• Лучшая производительность случая O (n log n) или O (n) с трехсторонним разделом
• Средняя производительность корпуса O (n log n)
  Back to Top

2.2 - Алгоритм карьера

• Полезная ссылка
  Идея алгоритма основана на концепции сокращения края (u, v) в неориентированном графике g = (v, e). Неофициально говоря, сокращение края объединяет узлы U и V в один, уменьшая общее количество узлов графика одним. На рисунке ниже показано, как работает сокращение. На слева на рисунке два смелых черных узла сливаются в один (подпрограмма справа).

Ключевая идея
Повторяя время алгоритма сокращения с независимыми случайными вариантами и возвращая наименьший сокращение, вероятность отсутствия минимального разреза
Характеристики

• С высокой вероятностью мы можем найти все сокращения мин во время выполнения
• Не находить вероятность нарезания мин - это время.
  Back to Top

3.0 - Структуры данных

Размещать структуры данных как независимый раздел вводит в заблуждение; Тем не менее, я введу проблемы с озадачивающимися проблемами, которые элегантно решаются структурами данных. Некоторые структуры данных могут иметь стратегию разработки алгоритма, которая еще не была рассмотрена.

3.1 - Первый поиск в очереди и ширине

• Полезный Link1 Link2
  Очередь, также известная как FIFO, является аббревиатурой для First In, сначала, метод организации и манипулирования буфером данных, где сначала обрабатывается самая старая (первая) запись или «голова» очереди.

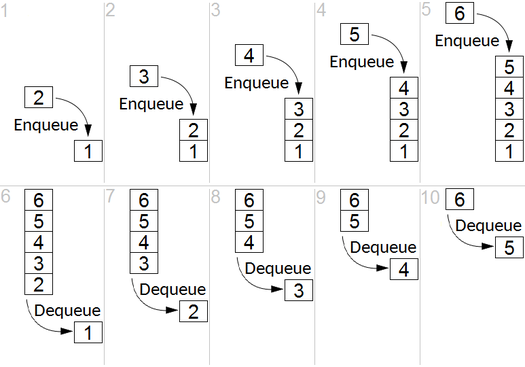
Ключевая идея
BFS используется для подсчета достижимых узлов из исходного узла в неисправном или направленном графике. Достигаемые узлы напечатаны в найденном порядке. Очередь используется для хранения серых узлов (см. GIF ниже). Термин «ширина» в BFS означает поиск достижимого узла с самой короткой длиной. Ширина расширяет границу между посещаемыми узлами и неоткрытыми узлами.

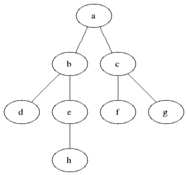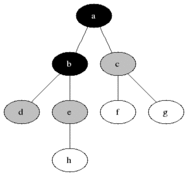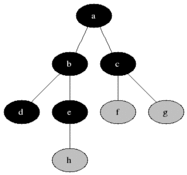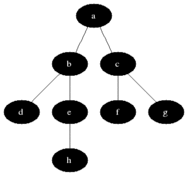
Характеристики

• Время работы: t (n) = o (v+e), v - количество вершин, e - количество краев
  Back to Top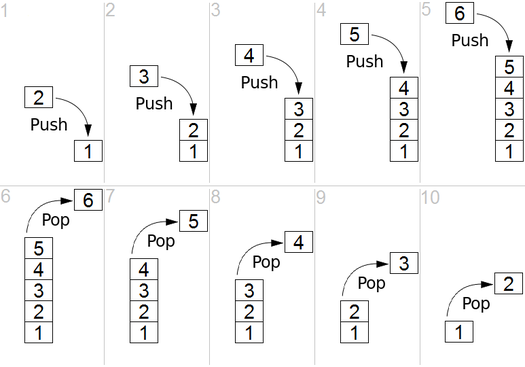

3.2 - стек и глубина первого поиска

• Полезный Link1 Link2
  Стек, также известный как Lifo, обладает собственностью Last In, сначала.
  

Ключевая идея
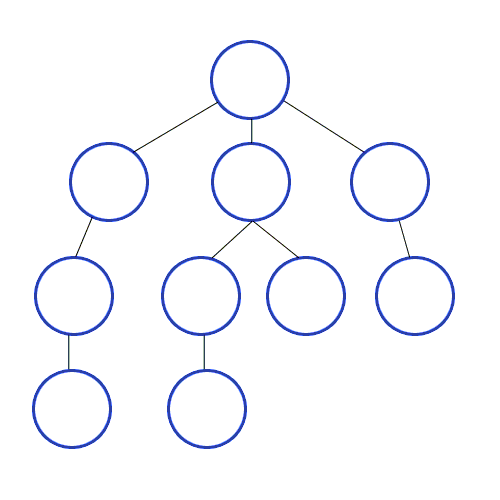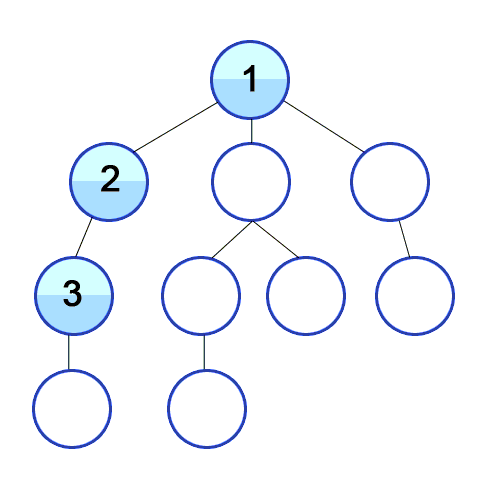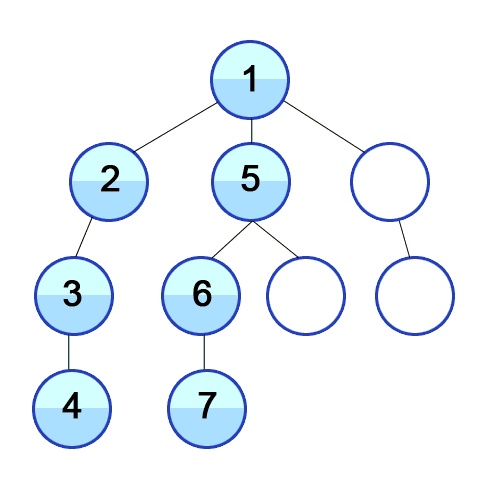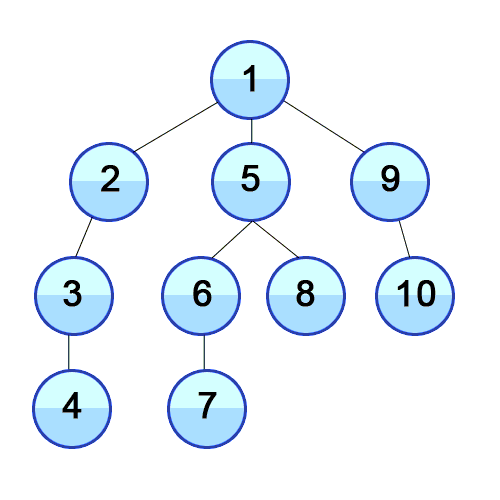
И DFS используется в направленном графике и сообщает, сколько узлов может достичь исходного узла, и распечатайте их по заказу, который мы их найдем. Мы используем стек для хранения узлов, которые мы классифицируем как начальные точки для графика. «Глубина» в его имени означает, что этот алгоритм пойдет так глубоко, как и для данного источника, и когда он достигнет конечной точки, он возвращается к начальному узлу.

Характеристики

• Время работы: t (n) = o (v+e), v - количество вершин, e - количество краев
  Back to Top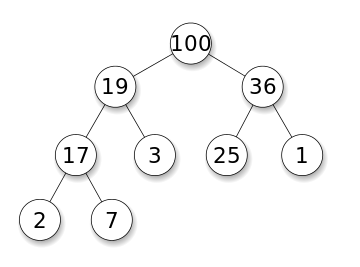

3.3 - Куча и медианное обслуживание

• Полезный Link1 Link2
  Куча-это специализированная структура данных на основе деревьев, которая удовлетворяет свойству кучи: если P-родительский узел C, то ключ (значение) P будет либо больше, либо равным (в максимальной куче), либо меньше или равным (в мине-куче) ключ C. [1] Узел в «верхней части» кучи (без родителей) называется корневым узлом.

Средняя проблема обслуживания состоит в том, что если целые числа считываются из потока данных, найдите медиану элементов, читаемые так для эффективного способа. Для простоты предположим, что нет дубликатов.

Ключевая идея
Мы можем использовать максимальную кучу на левой стороне, чтобы представлять элементы, которые менее чем эффективны, и кучу мин на правой стороне, чтобы представлять элементы, которые больше, чем эффективная медиана. Когда разница между размером двух кучей больше или равна 2, мы переключаем один элемент на другую кучу меньшего размера.

Характеристики

• Время работы:
  Back to Top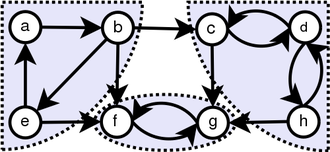

3.4 - сильно связанный компонент

• Полезная ссылка
  Направленный график называется тесно связанным, если в каждом направлении есть путь между каждой парой вершин графика. В направленном графике G, который сам по себе не может быть тесно связан, пара вершин U и V, как говорят, тесно связаны друг с другом, если в каждом направлении есть путь в каждом направлении.

Ключевая идея
Благодаря простому наблюдению, мы обнаруживаем, что Tranpose of Graph имеет те же SCCS, что и исходный график. Мы запускаем DFS дважды. Впервые мы запускаем его на G и вычислите время отделки для каждой вершины. И затем мы запускаем DFS на G^T, но в основной цикле DFS рассмотрим вершины в порядке уменьшения времени отделки.
Характеристики

• Время работы:, V - количество вершин, E - количество краев
  Back to Top

3.5 - Discoint -Set и SCC

• Полезная ссылка
  Структура данных, установленная в невысоке, также называемая структурой данных и набором данных Union-Find или набором слияния, представляет собой структуру данных, которая отслеживает набор элементов, разделенных на ряд непересекающихся подмножеств.
  Для наивного нереализованного набора, он поддерживает две основные операции: сет и союз. Сделать набор делает каждую вершину независимой группой. Юнион помещает две вершины в одну группу.

Ключевая идея
На неориентированном графике мы можем использовать эту структуру данных, чтобы выяснить, сколько SCC. На рисунке ниже показано, как это работает.

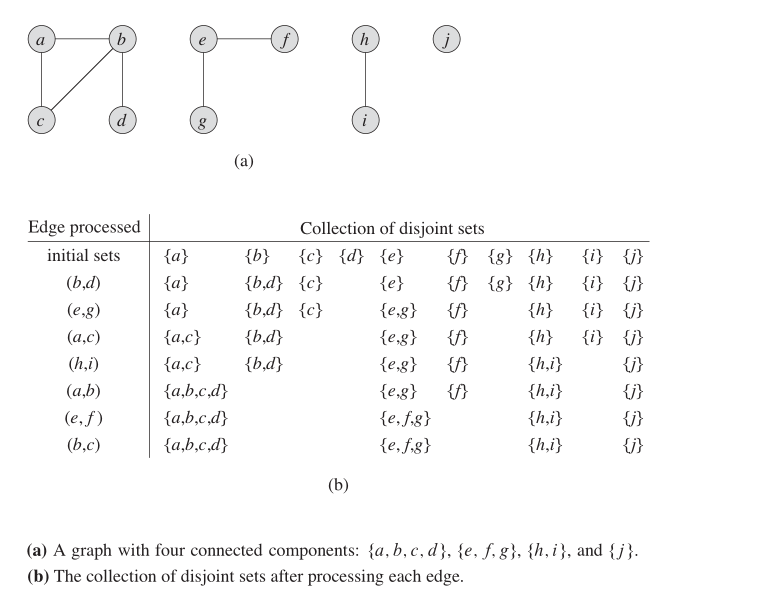
Характеристики

• Мы можем использовать эвристику с взвешенным союзом, чтобы сэкономить время, когда вызов
• Сжатие пути может значительно повысить эффективность времени находки профсоюзов
  Back to Top

4.0 - жадные алгоритмы

В этом разделе я собираюсь ввести жадные алгоритмы, одну мощную стратегию дизайна алгоритма.
Из Википедии жадный алгоритм представляет собой алгоритмическую парадигму, которая следует за эвристикой решения проблем, позволяющей сделать локально оптимальный выбор на каждом этапе [1] с надеждой найти глобальный оптимум. Во многих проблемах жадная стратегия в целом не производит оптимальное решение, но, тем не менее, жадная эвристика может дать локально оптимальные решения, которые приближаются к глобальному оптимальному решению в разумное время.

4.1 -

В проблеме выбора активности каждое действие имеет свой вес и длину. И наша цель - минимизировать сумму веса*длины. Это очень простой и отличный пример, чтобы показать, как работает жадный алгоритм, и предоставить элегантное доказательство с использованием техники обмена аргументами.
Ключевая идея
Если мы сортируем активность по значению веса/длины, мы можем доказать, что существующая оптимальная структура не может быть лучше, чем это расположение.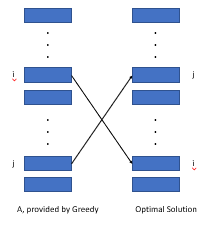

Как показано выше, мы рассмотрим стоимость, вызванные двумя видами деятельности, которые по -разному варьируются в двух расположениях (i, j). Мы обнаруживаем, что стоимость жадного алгоритма меньше оптимальной структуры по значению wi*lj - wj*li, что больше или равно 0.

Характеристики

• Время работы преобладает сортировка
  Back to Top

4.2 - Выбор активности

• Полезная ссылка
  В этой проблеме каждое занятие имеет свое время начала и время завершения. Наша цель состоит в том, чтобы выбрать подмножество максимальной длины, где рабочие места совместимы.
  

Ключевая идея
Мы отсортировали массив в соответствии с его временем завершения. Алгоритм поместил первую работу, время начала которого больше, чем время за последней работой.
Характеристики

• Время работы рекурсивного выбора активности
  Back to Top

4.3 - Кодирование Хаффмана

• Полезная ссылка
  Код Huffman - это конкретный тип оптимального кода префикса, который обычно используется для сжатия данных без потерь. Например, в таблице ниже показана частота букв в «книге».

Один из способов кодирования этой книги - использовать кодирование фиксированной длины. Как показано ниже:

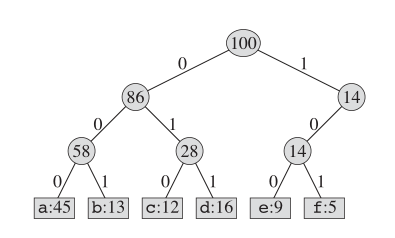
Что касается кодирования Хаффмана, реальная структура дерева выглядит следующим образом:

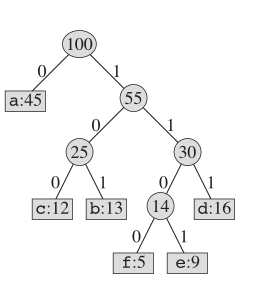
Ключевая идея
Мы поддерживаем двоичное дерево и создаем новый узел в качестве родителя для двух наименее нечастого буква. И ключом для этого нового узла является сумма ключей для двух детей. Мы повторяем это, пока в этой «книге» не осталось узлов.

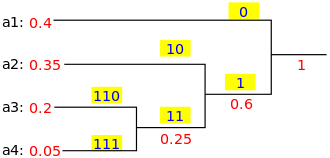
Характеристики

• Процедура Хаффман создает оптимальный код префикса
  Back to Top

4.4 - алгоритм Dijkstra

• Полезная ссылка
  

Алгоритм Дейкстры является алгоритмом для поиска кратчайших путей между узлами на графике. Тем не менее, он имеет одну предпосылку, все пути должны быть больше или равны 0.

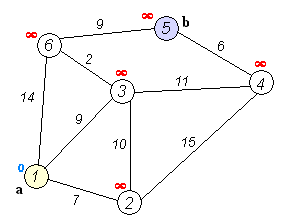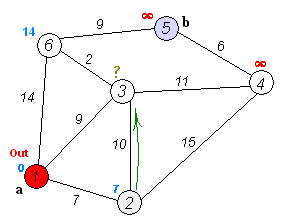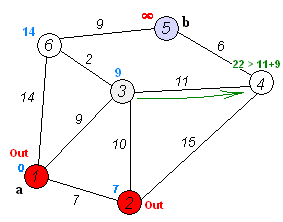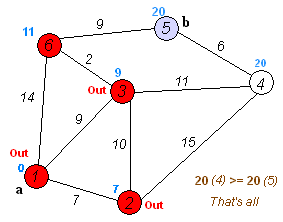
Ключевая идея
Отдельные узлы в две группы, одна группа отмечена как исследованная. И мы обновляем расстояние от неисследованной группы до изучения группы на кратчайшие расстояния.

Характеристики

• Время работы в зависимости от очереди Min-приоритета, реализованной кучей Fibonacci
  Back to Top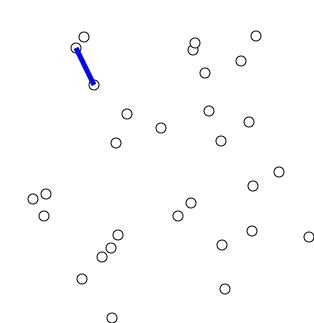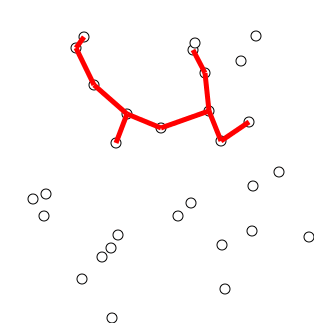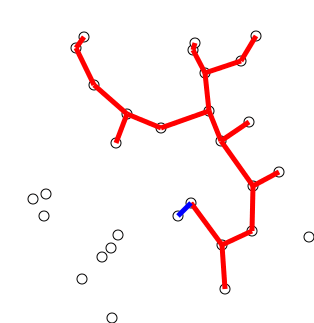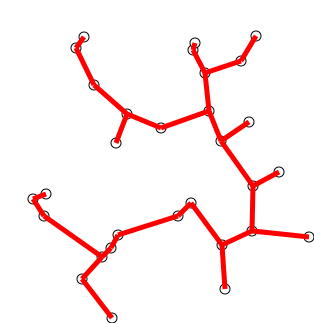

4.5 - Алгоритм PRIM

• Полезная ссылка
  Алгоритм PRIM является жадным алгоритмом, который находит минимальное охватывающее дерево для взвешенного неистового графика. Очень похоже на алгоритм Dijkstra, мы поддерживаем два набора, исследовали один и неисследованный. Каждый раз мы поглощаем только вершину, которая имеет наименьшее расстояние для изучения набора. Это очень четко показано на рисунке ниже:

Ключевая идея
Алгоритм можно неформально описать как выполнение следующих шагов:

Инициализируйте дерево с одной вершиной, выбранной произвольно из графика.
Вырастите дерево одним краем: из краев, которые соединяют дерево с вершинами, еще не в дереве, найдите минимальный края и перенесите его на дерево.
Повторите шаг 2 (пока все вершины не будут в дереве).

Характеристики

• Время работы

• Матрица смежности, поиск
• Бинарная куча и смежность списка
• Список кучи и смежности Фибоначчи
  Back to Top

4.6 - Алгоритм Крускала и проблема кластеризации

• Полезная ссылка
  Алгоритм PRIM является еще одним жадным алгоритмом, который находит минимальное дерево охватывающих для взвешенного неистового графика. Вместо того, чтобы поддерживать дерево, подобное первому, оно поддерживает лес.

Ключевая идея
Очень похоже на SCC, мы можем раннее остановить алогрифм, чтобы контролировать количество классов в нашем графике, то есть мы можем снять график.

Характеристики

• Время работы O (ELOGV)
  Back to Top

5.0 - Динамическое программирование

В этом разделе я собираюсь ввести динамические алгоритмы, одну мощную стратегию дизайна алгоритмов.
Из Википедии динамическое программирование (также известное как динамическая оптимизация) - это метод решения сложной проблемы, разбивая ее на набор более простых подпроектов, решая каждую из этих подзадач только один раз и сохраняя свои решения.

5.1 - Резка стержня

• Полезная ссылка
  Учитывая стержень длины n дюймов и множество цен, которые содержат цены на все части размера меньше n. Определите максимальное значение, которое можно получить, разрезая стержень и продав кусочки.
  Следующая таблица показывает взаимосвязь между ценой и длиной.

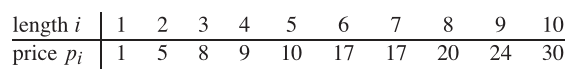
Таким образом, если длина стержня составляет 8, а значения различных частей задаются следующим образом, то максимально достижимое значение составляет 22 (по разрезанию двух частей длины 2 и 6).

Ключевая идея
Мы рассматриваем разложение как состоящую из первого куска длины, я отрезал левый конец, а затем правую оставшуюся часть длины n-i. Итак, псевдокод выглядит как:

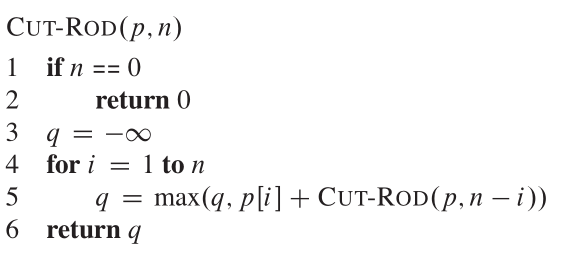
Дерево рекурсии, показывающее рекурсивные вызовы, возникающие в результате вызова cut_rod (p, n), выглядит как:

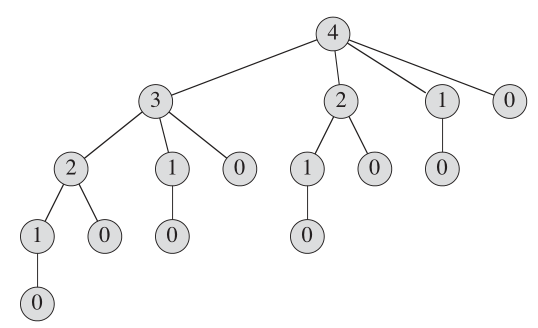
Чтобы сохранить повторные вычисления для небольших подпрограмм, мы запомнили массив для хранения этих значений.

Характеристики

• Временная сложность приведенной выше реализации составляет O (n^2)
  Back to Top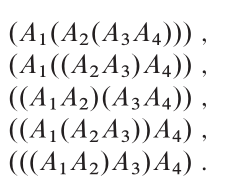

5.2 - умножение матричной цепи

• Полезная ссылка
  Умножение матричной цепи (или задача по упорядочению цепочки матрицы, MCOP) - это проблема оптимизации, которую можно решить с помощью динамического программирования. Учитывая последовательность матриц, цель состоит в том, чтобы найти наиболее эффективный способ умножения этих матриц. Проблема на самом деле заключается не в том, чтобы выполнить умножения, а просто для определения последовательности участвующих умножений матрицы.

Ключевая идея
Оптимальная структура:

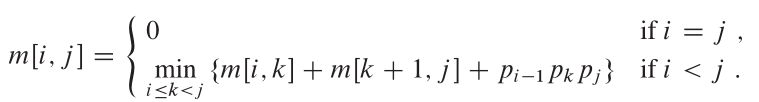
Характеристики

• Временная сложность приведенной выше реализации
  Back to Top

5.3 - Самая длинная общая последующая последовательность

• Полезная ссылка
  Самая длинная проблема общей последующей последовательности (LCS) - это проблема поиска самой длинной последующей последовательности, общей для всех последовательностей в наборе последовательностей (часто только две последовательности).

Ключевая идея
Из CLR оптимальная структура для этой проблемы такова:

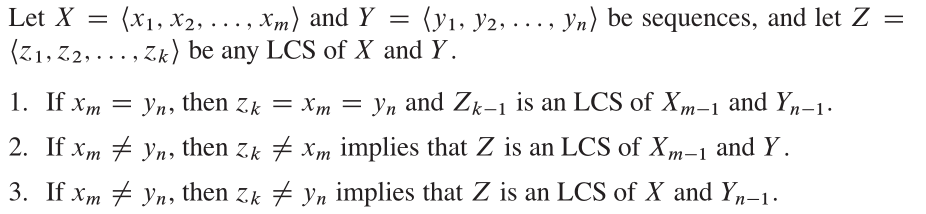
Характеристики

• Временная сложность приведенной выше реализации $ theta (mn) $
  Back to Top

5.4 - Алгоритм Флойд -Варшалла

• Полезная ссылка
  Алгоритм Floyd -Warshall является алгоритмом для поиска самых коротких путей на взвешенном графике с положительным или отрицательным весом края (но без отрицательных циклов).

Ключевая идея
Этот алгоритм основан на очень интуитивном наблюдении. Предположим, у нас есть подмножество {1, 2, 3, 4, ..., k} (обозначает как v (k)) оригинальной группы вершин {1, 2, 3, ..., n}. Если P - самый короткий путь от I до J в V (k), у нас есть два случая. Во-первых, если K не в P, то P должен быть кратчайшим путем в V (K-1). Во -вторых, если K находится в P, то мы можем разделить путь на два, p1: i K, P2: K. Дж. и P1 должен быть самым коротким путем от I до K с V (K-1), P2 должен быть самым коротким путем от K до J с V (K-1).

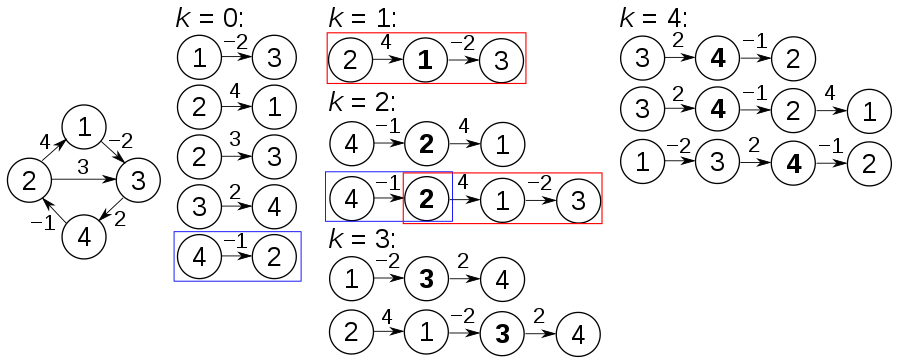
Характеристики

• Временная сложность приведенной выше реализации
  Back to Top

6.0 - Алгоритмы приближения для NPC

Из Wikipedia проблема с решением NP-это та, которая принадлежит как к классам сложности NP, так и к NP-Hard. В этом контексте NP означает «неэнергинизм полиномиального времени». Набор задач NP-полных часто обозначается NP-C или NPC.

В этом разделе я собираюсь представить три очень известные проблемы NPC и объяснить алгоритмы приближения, чтобы приблизиться к ним.

6.1 - крышка вершины

• Полезная ссылка
  Крышка вершины (иногда крышка узла) графика представляет собой набор вершин, так что каждый край графика зависит как минимум с одной вершиной набора. На рисунке ниже показано минимальная крышка вершины (где набор крышки должен иметь как минимум две версии, ноль и никто не поможет).

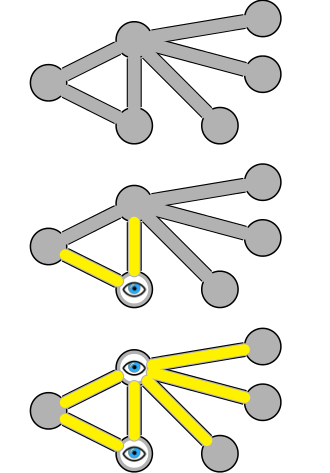
Ключевая идея
Очень сложно найти минимальную крышку вершины, но мы можем найти приблизительное покрытие с большим вдвое больше вершин в полиномиальное время.

Характеристики

• Appor-vertex-cover-это алгоритм полиномиального времени 2-ореама.
  Back to Top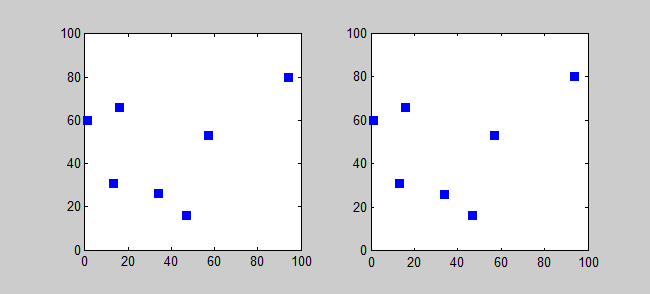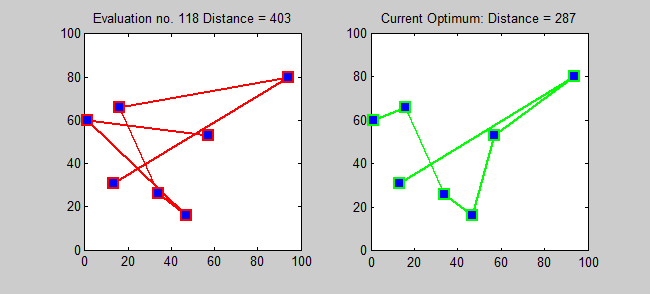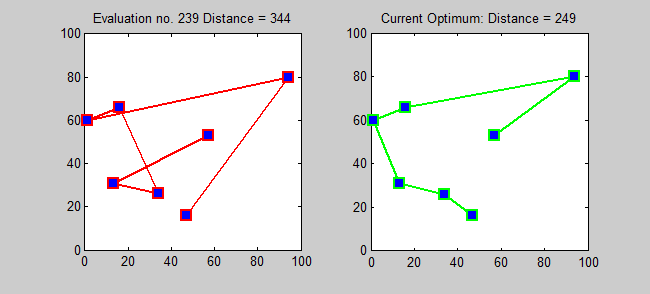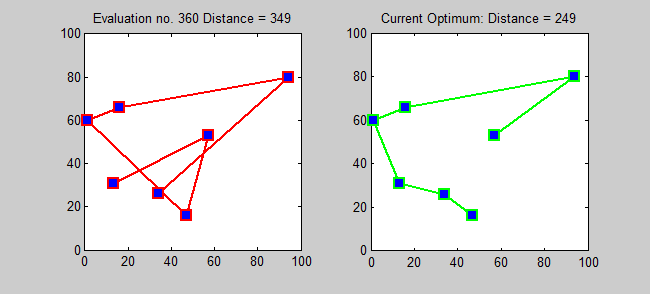

6.2 - Проблема с продавцом -путешественниками

• Полезная ссылка
  Проблема переезда продавца (TSP) задает следующий вопрос: «Учитывая список городов и расстояния между каждой парой городов, какой самый короткий возможный маршрут, который посещает каждый город и возвращается в город происхождения?» GIF показывает грубую силу для TSP.

Ключевая идея
Алгоритм приближения для TSP представляет собой жадный алгоритм (CLRS P1114). Здесь я также хочу представить точный алгоритм для TSP с использованием динамического программирования.

Подпрозрачная: для каждого пункта назначения j ∈ {1,2, ..., n}, каждое подмножество s ⊆ {1,2, ..., n}, которое содержит 1 и j, пусть ls, j = минимальная длина пути от 1 до J, который посещает именно вершины S [точно один раз каждый]. Итак, соответствующий рецидив:

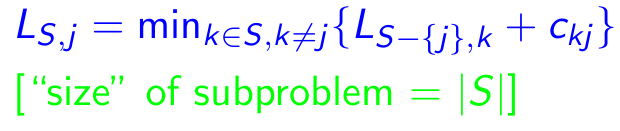
Характеристики

• Время работы точного алгоритма:
  Back to Top

6.3 - Проблема логической удовлетворенности

• Полезная ссылка
  Проблема удовлетворенности логины (иногда называемая проблемой удовлетворенности и сокращением как удовлетворенность или SAT) является проблемой определения, существует ли интерпретация, которая удовлетворяет данной логической формуле.

3-SAT является одной из 21 задач KARP, и используется в качестве отправной точки для доказательства того, что другие проблемы также являются NP-Hard.

Здесь я представляю алгоритм Papadimitriou для 2-сат (это очень-очень-очень интересный алгоритм , поэтому я решаю представить его, хотя 2-сат не NPC).

Ключевая идея
Выберите случайное начальное назначение и выберите произвольный неудовлетворенный пункт и переверните значение одной из ее переменной. Вот псевдокод:

Такое случайное дело с предложениями удивительно даст нам очень большую вероятность найти реальный ответ. Механизм лежит в физическом термине (случайная прогулка). Если вы заинтересованы, я настоятельно рекомендую вам рассказать, как случайная прогулка связана с пападимитриу.

Характеристики

• Для удовлетворенного экземпляра 2-сат с n переменными алгоритм Пападимитриу создает удовлетворительное назначение с вероятностью ≥ 1-1/n
• Пробегает в полиномиальное время
• Всегда верните в неудовлетворительных случаях
  Back to Top