ที่เก็บนี้ฉันจะใช้ Python เพื่อใช้อัลกอริทึมที่มีชื่อเสียง อัลกอริทึมถูกจัดเรียงตามกลยุทธ์ที่ใช้ อัลกอริทึมแต่ละตัวจะมีคำอธิบายเกี่ยวกับปัญหาที่พยายามแก้ปัญหาและทรัพยากรที่เกี่ยวข้อง
(เป้าหมายของที่เก็บนี้คือการสร้าง readme ที่สวยงามสำหรับอัลกอริทึมที่ยอดเยี่ยมเหล่านี้ทั้งหมดที่ฉันได้ตรวจสอบ)
เนื้อหา:
ส่วนนี้ฉันจะพูดคุยเกี่ยวกับกลยุทธ์การแบ่งแยกและพิชิตที่มีชื่อเสียงและแสดงแอปพลิเคชันบางอย่างของกลยุทธ์นี้
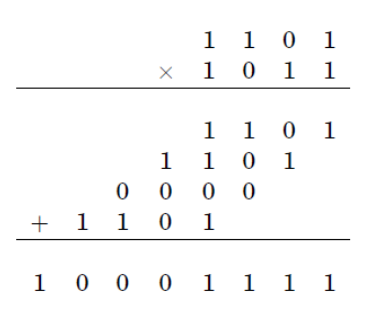
ขั้นตอนมาตรฐานสำหรับการคูณของตัวเลข N สองตัวเลขต้องใช้จำนวนการดำเนินงานเบื้องต้นตามสัดส่วน สำหรับอัลกอริทึม Karatsuba จะช่วยลดเวลาทำงานได้มากที่สุด
ความคิดหลัก ๆ
ขั้นตอนพื้นฐานของอัลกอริทึมของ Karatsuba เป็นสูตรที่ช่วยให้หนึ่งสามารถคำนวณผลิตภัณฑ์ของตัวเลขจำนวนมากสองตัวและใช้การคูณของตัวเลขที่เล็กกว่าสามครั้งแต่ละตัวมีตัวเลขประมาณครึ่งหลักเป็นหรือรวมถึงการเพิ่มเติมและการเปลี่ยนแปลงหลัก
คุณสมบัติ
Back to Top
เวลาทำงานที่เลวร้ายที่สุดสำหรับอัลกอริทึมนี้คือ
GIF ด้านบนแสดงให้เห็นว่าการเรียงลำดับการทำงานแบบผสานทำงานอย่างไร: 
ความคิดหลัก ๆ
แบ่งรายการที่ไม่ได้เรียงลำดับออกเป็น n sublist แต่ละรายการที่มี 1 องค์ประกอบ (รายการ 1 องค์ประกอบได้รับการพิจารณาเรียงลำดับ) และรวม sublists ซ้ำ ๆ เพื่อผลิต sublist ที่เรียงลำดับใหม่จนกว่าจะมีเพียง 1 sublist ที่เหลืออยู่ นี่จะเป็นรายการเรียงลำดับ
คุณสมบัติ
Back to Top
ความคิดหลัก ๆ
เช่นเดียวกับรูปด้านบนเมื่อเราใช้องค์ประกอบจากการอาร์เรย์ย่อยที่ถูกต้องเป็นครั้งแรกในการดำเนินการผสานซึ่งบ่งชี้ว่าองค์ประกอบด้านขวามีขนาดเล็กกว่า (ความยาวของการอาเรย์ย่อยซ้าย-ดัชนีขององค์ประกอบด้านซ้าย)
เมื่ออัลกอริทึมดำเนินไปเพิ่มการรุกรานทั้งหมดจะทำให้เรามีการรุกรานทั้งหมด
คุณสมบัติ
Back to Top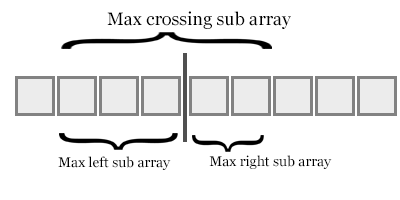
คุณสมบัติ
Back to Topส่วนนี้ฉันจะพูดถึงอัลกอริทึมสองตัวที่ใช้ตัวแปรสุ่มภายใน
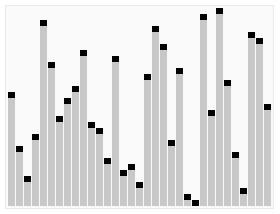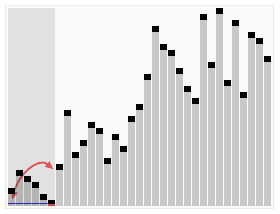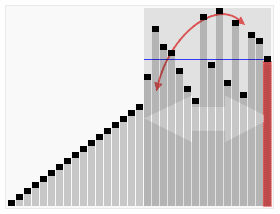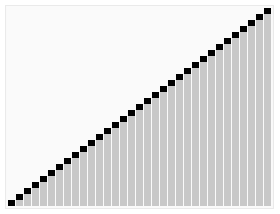
ความคิดหลัก ๆ
Quicksort ก่อนแบ่งอาเรย์ขนาดใหญ่ออกเป็นสองอาร์เรย์ขนาดเล็กสองอัน: องค์ประกอบต่ำและองค์ประกอบสูงที่สัมพันธ์กับองค์ประกอบที่เลือกแบบสุ่ม Quicksort สามารถจัดเรียงอาร์เรย์ย่อยซ้ำได้ ดังนั้นจุดสำคัญในการเรียงลำดับอย่างรวดเร็วคือการเลือกองค์ประกอบพาร์ติชัน
คุณสมบัติ
Back to Top
ความคิดหลัก ๆ
ด้วยการทำซ้ำอัลกอริทึมการหดตัวด้วยตัวเลือกแบบสุ่มอิสระและส่งคืนการตัดที่เล็กที่สุดความน่าจะเป็นที่จะไม่พบการตัดขั้นต่ำคือ
คุณสมบัติ
Back to Topการวางโครงสร้างข้อมูลเป็นส่วนที่เป็นอิสระทำให้เข้าใจผิด อย่างไรก็ตามฉันจะแนะนำปัญหาที่น่างงงวยซึ่งได้รับการแก้ไขอย่างหรูหราโดยโครงสร้างข้อมูล โครงสร้างข้อมูลบางอย่างอาจมีกลยุทธ์การออกแบบอัลกอริทึมที่ยังไม่ได้รับการตรวจสอบ
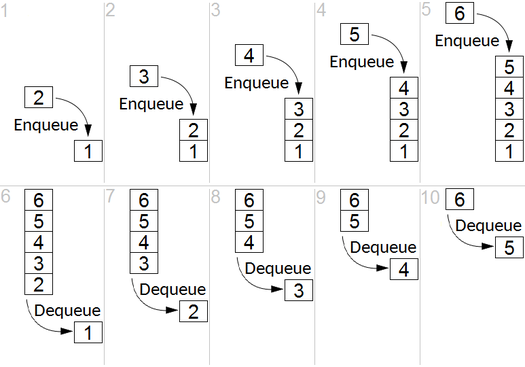
ความคิดหลัก ๆ
BFS ใช้เพื่อนับโหนดที่เข้าถึงได้จากโหนดต้นทางในกราฟที่ไม่ได้กำกับหรือกำกับ โหนดที่เข้าถึงได้จะถูกพิมพ์ตามลำดับที่พบ คิวใช้เพื่อเก็บสีเทาสีโหนด (ดู GIF ด้านล่าง) คำว่า "ความกว้าง" ใน BFS หมายถึงการค้นหาโหนดที่เข้าถึงได้ด้วยความยาวที่สั้นที่สุด ความกว้างขยายขอบเขตระหว่างโหนดที่เข้าชมและโหนดที่ยังไม่ได้เปิด
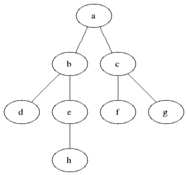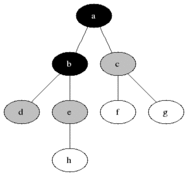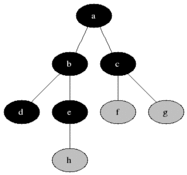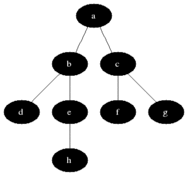
คุณสมบัติ
Back to Top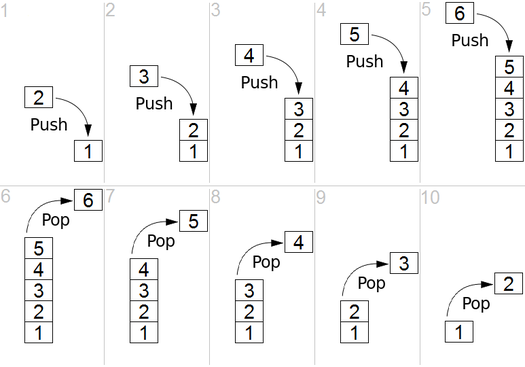
ความคิดหลัก ๆ
และ DFS ถูกใช้ในกราฟกำกับและบอกว่าโหนดแหล่งกำเนิดสามารถเข้าถึงและพิมพ์ได้กี่โหนดตามลำดับที่เราพบ เราใช้สแต็กเพื่อจัดเก็บโหนดที่เราจัดประเภทเป็นจุดเริ่มต้นสำหรับกราฟ "ความลึก" ในชื่อของมันหมายความว่าอัลกอริทึมนี้จะไปอย่างลึกซึ้งที่สุดเท่าที่จะทำได้สำหรับแหล่งที่มาและเมื่อถึงจุดสิ้นสุดมันจะกลับไปที่โหนดเริ่มต้น
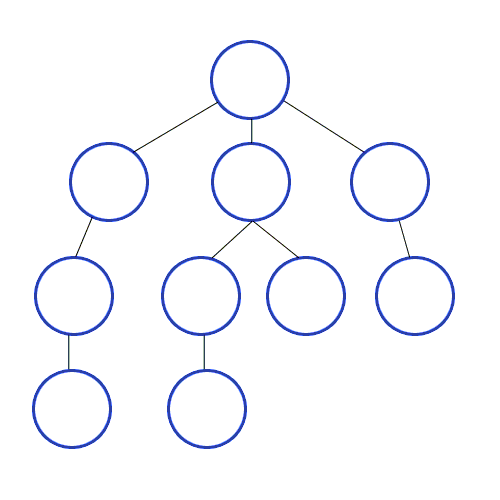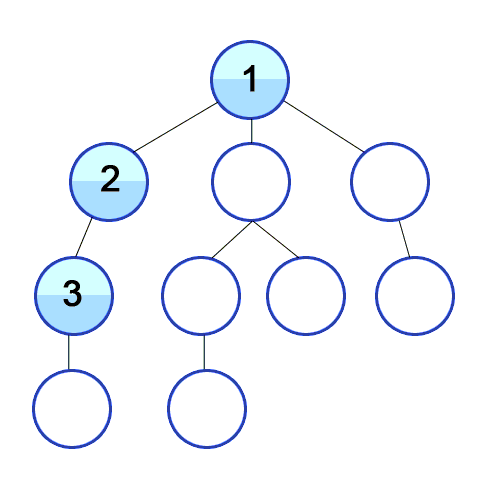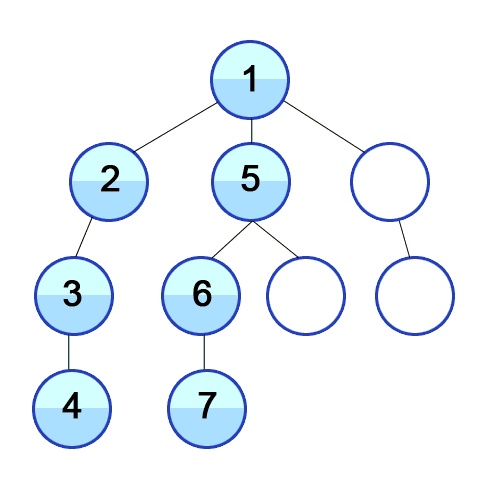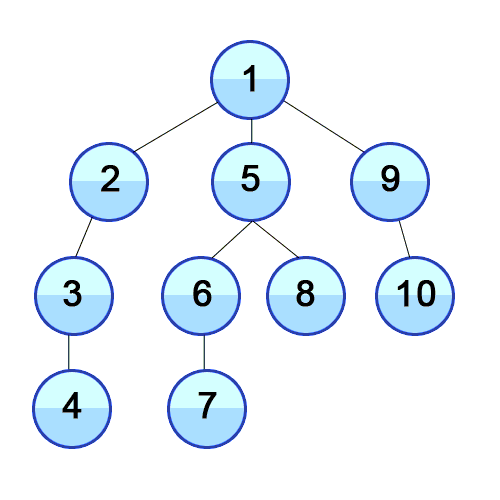
คุณสมบัติ
Back to Top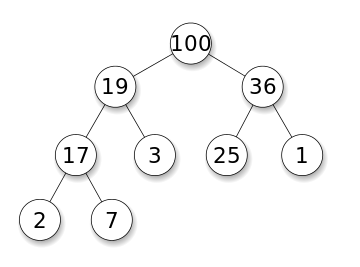
ปัญหาการบำรุงรักษาค่ามัธยฐานคือถ้าจำนวนเต็มถูกอ่านจากกระแสข้อมูลให้ค้นหาค่ามัธยฐานขององค์ประกอบที่อ่านได้อย่างมีประสิทธิภาพ เพื่อความเรียบง่ายสมมติว่าไม่มีการทำซ้ำ
ความคิดหลัก ๆ
เราสามารถใช้กองสูงสุดทางด้านซ้ายเพื่อเป็นตัวแทนขององค์ประกอบที่น้อยกว่าค่ามัธยฐานที่มีประสิทธิภาพและกองนาทีด้านขวาเพื่อแสดงองค์ประกอบที่มากกว่าค่ามัธยฐานที่มีประสิทธิภาพ เมื่อความแตกต่างระหว่างขนาดของสองกองสูงกว่าหรือเท่ากับ 2 เราจะสลับองค์ประกอบหนึ่งเป็นกองขนาดเล็กกว่าอื่น
คุณสมบัติ
Back to Top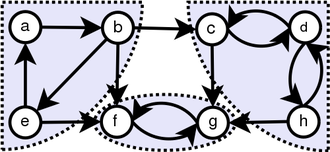
ความคิดหลัก ๆ
จากการสังเกตอย่างง่ายเราพบว่า tranpose ของกราฟมี SCCs เดียวกับกราฟดั้งเดิม เราเรียกใช้ DFS สองครั้ง ครั้งแรกเราเรียกใช้กับ G และคำนวณเวลาจบสำหรับแต่ละจุดสุดยอด จากนั้นเราเรียกใช้ dfs บน g^t แต่ในห่วงหลักของ DFS ให้พิจารณาจุดยอดตามลำดับเวลาที่ลดลง
คุณสมบัติ
Back to Top
ความคิดหลัก ๆ
ในกราฟที่ไม่ได้กำกับเราสามารถใช้โครงสร้างข้อมูลนี้เพื่อค้นหาจำนวน SCC รูปด้านล่างแสดงวิธีการทำงาน
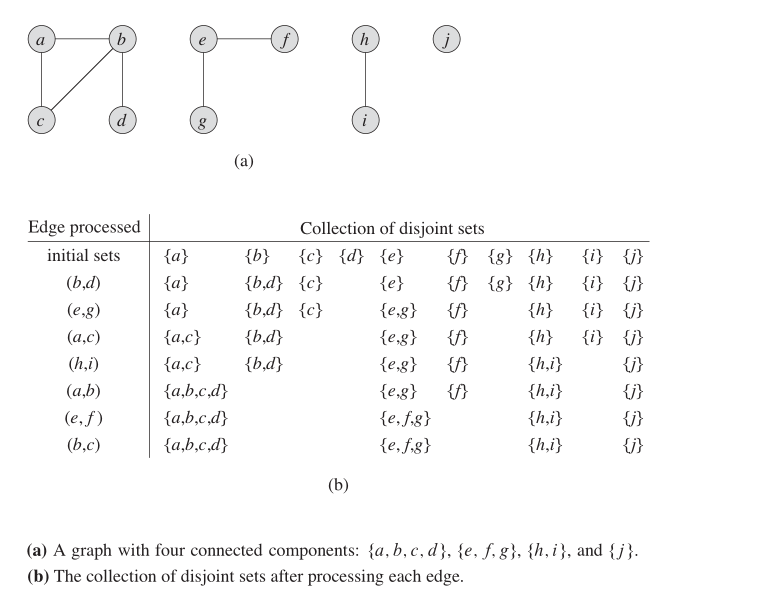
คุณสมบัติ
Back to Top ในส่วนนี้ฉันจะแนะนำอัลกอริทึมโลภซึ่งเป็นกลยุทธ์การออกแบบอัลกอริทึมที่ทรงพลังอย่างหนึ่ง
จาก Wikipedia อัลกอริทึมโลภเป็นกระบวนทัศน์อัลกอริทึมที่ตามมาด้วยการแก้ปัญหาการแก้ปัญหาการเลือกที่ดีที่สุดในท้องถิ่นในแต่ละขั้นตอน [1] ด้วยความหวังว่าจะได้พบกับที่ดีที่สุดทั่วโลก ในปัญหาหลายอย่างกลยุทธ์โลภไม่ได้ผลิตทางออกที่ดีที่สุดโดยทั่วไป แต่ถึงกระนั้นก็ตามฮิวริสติกโลภอาจให้โซลูชั่นที่ดีที่สุดในท้องถิ่น
ในปัญหาการเลือกกิจกรรมทุกกิจกรรมมีน้ำหนักและความยาวของตัวเอง และเป้าหมายของเราคือลดผลรวมของน้ำหนัก* มันเป็นตัวอย่างที่ง่ายและยอดเยี่ยมในการแสดงให้เห็นว่าอัลกอริทึมโลภทำงานได้อย่างไรและให้การพิสูจน์ที่หรูหราโดยใช้เทคนิคการแลกเปลี่ยนอาร์กิวเมนต์
ความคิดหลัก ๆ
หากเราเรียงลำดับกิจกรรมตามค่าน้ำหนัก/ความยาวเราสามารถพิสูจน์โครงสร้างที่ดีที่สุดที่มีอยู่ไม่สามารถดีกว่าการจัดเรียงนี้ 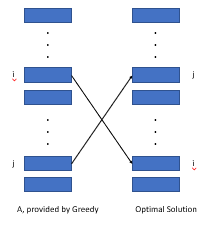
ดังที่แสดงไว้ข้างต้นเราพิจารณาค่าใช้จ่ายที่เกิดจากสองกิจกรรมที่อยู่ในช่วงแตกต่างกันในสองข้อ (i, j) เราพบว่าค่าใช้จ่ายในอัลกอริทึมโลภมีขนาดเล็กกว่าโครงสร้างที่ดีที่สุดโดยค่าของ wi*lj - wj*li ซึ่งมากกว่าหรือเท่ากับ 0
คุณสมบัติ
Back to Top
ความคิดหลัก ๆ
เราจัดเรียงอาร์เรย์ตามเวลาเสร็จสิ้น อัลกอริทึมทำให้งานแรกที่เวลาเริ่มต้นใหญ่กว่าเวลาทำงานสุดท้ายของงาน
คุณสมบัติ
Back to Top
วิธีหนึ่งในการเข้ารหัสหนังสือเล่มนี้คือการใช้การเข้ารหัสความยาวคงที่ ดังที่แสดงด้านล่าง:
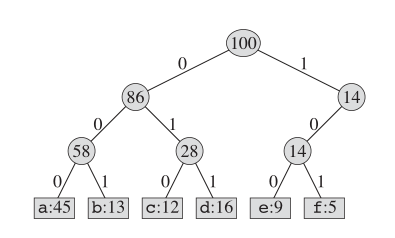
สำหรับการเข้ารหัส Huffman โครงสร้างต้นไม้ที่แท้จริงมีลักษณะเช่นนี้:
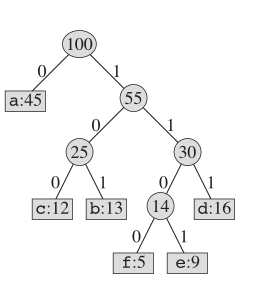
ความคิดหลัก ๆ
เรารักษาต้นไม้ไบนารีและสร้างโหนดใหม่เป็นพาเรนต์สำหรับตัวอักษรสองตัวน้อยที่สุด และกุญแจสำคัญสำหรับโหนดใหม่นี้คือผลรวมของกุญแจสำหรับเด็กสองคน เราทำซ้ำสิ่งนี้จนกว่าจะไม่มีโหนดเหลืออยู่ใน "หนังสือ" นี้
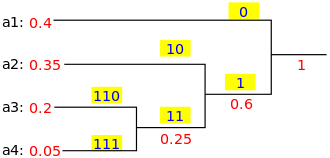
คุณสมบัติ
Back to Topอัลกอริทึมของ Dijkstra เป็นอัลกอริทึมสำหรับการค้นหาเส้นทางที่สั้นที่สุดระหว่างโหนดในกราฟ อย่างไรก็ตามมันมีข้อกำหนดเบื้องต้นหนึ่งเส้นทางจะต้องสูงกว่าหรือเท่ากับ 0
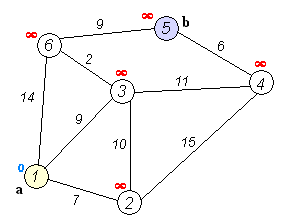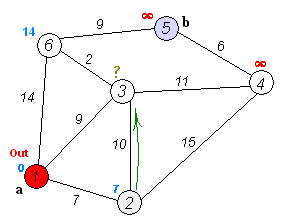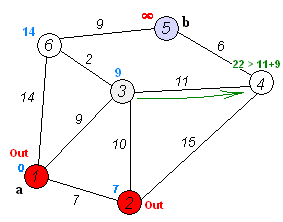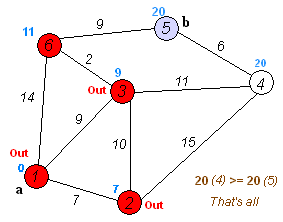
ความคิดหลัก ๆ
โหนดแยกออกเป็นสองกลุ่มกลุ่มหนึ่งถูกทำเครื่องหมายว่าสำรวจ และเราอัปเดตระยะทางจากกลุ่มที่ยังไม่ได้สำรวจไปยังกลุ่มสำรวจในระยะทางที่สั้นที่สุด
คุณสมบัติ
Back to Top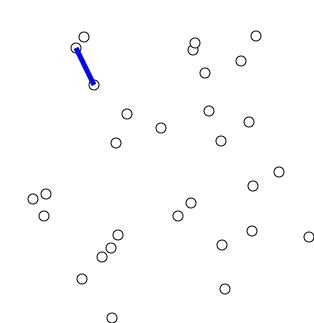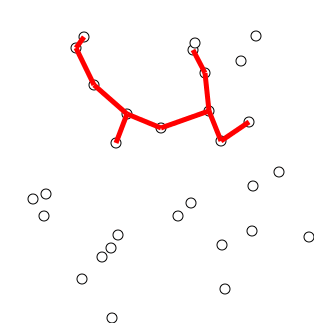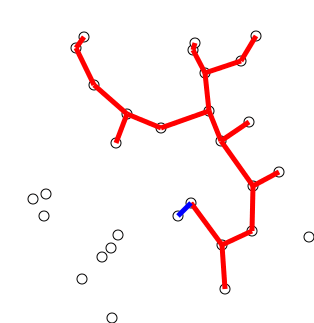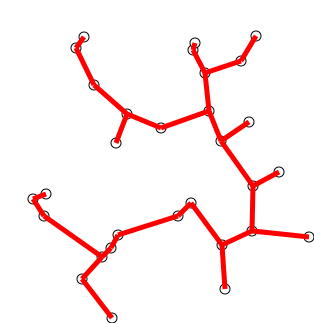
ความคิดหลัก ๆ
อัลกอริทึมอาจอธิบายอย่างไม่เป็นทางการว่าทำตามขั้นตอนต่อไปนี้:
เริ่มต้นต้นไม้ด้วยจุดสุดยอดเดียวที่เลือกโดยพลการจากกราฟ
ปลูกต้นไม้ด้วยขอบด้านเดียว: จากขอบที่เชื่อมต่อต้นไม้เข้ากับจุดยอดที่ยังไม่ได้อยู่ในต้นไม้ค้นหาขอบน้ำหนักต่ำสุดและถ่ายโอนไปยังต้นไม้
ทำซ้ำขั้นตอนที่ 2 (จนกว่าจุดยอดทั้งหมดจะอยู่ในต้นไม้)
คุณสมบัติ
Back to Top
ความคิดหลัก ๆ
คล้ายกับ SCC มากเราสามารถหยุด Alogrithm ได้ก่อนเพื่อควบคุมจำนวนคลาสในกราฟของเราซึ่งก็คือบอกว่าเราสามารถจัดกลุ่มกราฟได้
คุณสมบัติ
Back to Top ในส่วนนี้ฉันจะแนะนำอัลกอริทึมแบบไดนามิกซึ่งเป็นกลยุทธ์การออกแบบอัลกอริทึมที่ทรงพลังอย่างหนึ่ง
จาก Wikipedia การเขียนโปรแกรมแบบไดนามิก (หรือที่เรียกว่าการเพิ่มประสิทธิภาพแบบไดนามิก) เป็นวิธีการแก้ปัญหาที่ซับซ้อนโดยแบ่งมันออกเป็นคอลเลกชันของปัญหาย่อยที่ง่ายกว่าแก้ปัญหาย่อยเหล่านั้นเพียงครั้งเดียวและเก็บโซลูชันของพวกเขา
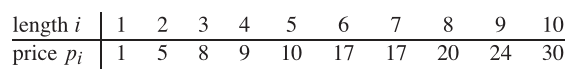
ดังนั้นหากความยาวของก้านคือ 8 และค่าของชิ้นส่วนต่าง ๆ จะได้รับดังต่อไปนี้ค่าสูงสุดที่หาได้คือ 22 (โดยการตัดในสองชิ้นของความยาว 2 และ 6)
ความคิดหลัก ๆ
เราดูการสลายตัวซึ่งประกอบด้วยความยาวชิ้นแรกที่ฉันตัดปลายซ้ายมือจากนั้นส่วนที่เหลืออยู่ทางขวาของความยาว n-i ดังนั้น pseudocode จึงดูเหมือนว่า:
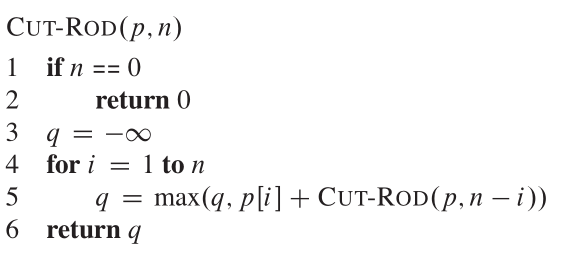
ต้นไม้เรียกซ้ำที่แสดงการโทรแบบเรียกซ้ำเป็นผลมาจากการโทร cut_rod (p, n) ดูเหมือนว่า:
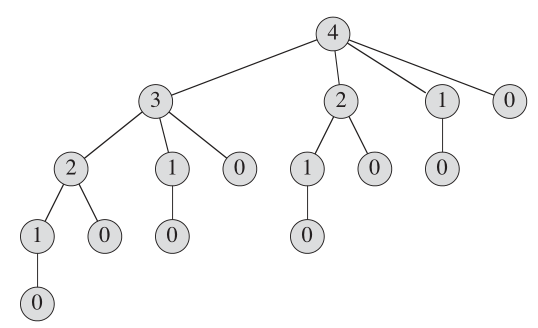
เพื่อบันทึกการคำนวณซ้ำสำหรับปัญหาย่อยขนาดเล็กเราได้จดจำอาร์เรย์เพื่อเก็บค่าเหล่านี้
คุณสมบัติ
Back to Top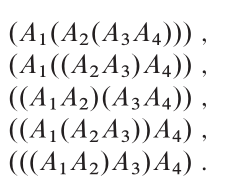
ความคิดหลัก ๆ
โครงสร้างที่ดีที่สุด:
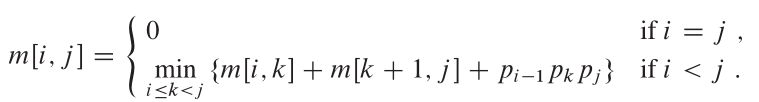
คุณสมบัติ
Back to Top ความคิดหลัก ๆ
จาก CLRS โครงสร้างที่ดีที่สุดสำหรับปัญหานี้คือ:
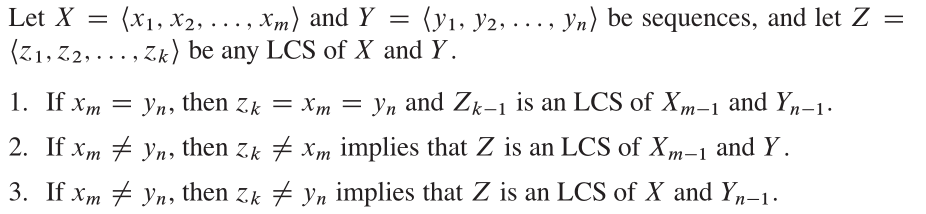
คุณสมบัติ
Back to Top ความคิดหลัก ๆ
อัลกอริทึมนี้ขึ้นอยู่กับการสังเกตที่ใช้งานง่ายมาก สมมติว่าเรามีชุดย่อย {1, 2, 3, 4, ... , k} (แสดงว่า V (k)) ของกลุ่มจุดยอดดั้งเดิม {1, 2, 3, ... , n} หาก P เป็นเส้นทางที่สั้นที่สุดจาก I ถึง J ใน V (K) เรามีสองกรณี ก่อนอื่นถ้า k ไม่ได้อยู่ใน P ดังนั้น p จะต้องเป็นเส้นทางที่สั้นที่สุดใน V (K-1) ประการที่สองถ้า k อยู่ใน p เราสามารถแยกเส้นทางออกเป็นสอง p1: i K, P2: K j. และ P1 จะต้องเป็นเส้นทางที่สั้นที่สุดจาก I ถึง K ด้วย V (K-1), P2 ต้องเป็นเส้นทางที่สั้นที่สุดจาก K ถึง J ด้วย V (K-1)
คุณสมบัติ
Back to Top จากจาก Wikipedia ปัญหาการตัดสินใจของ NP-complete เป็นหนึ่งในคลาส NP และคลาสความซับซ้อนของ NP-Hard ในบริบทนี้ NP หมายถึง "เวลาพหุนามแบบไม่ใช้เวลา" ชุดของปัญหา NP-complete มักแสดงโดย NP-C หรือ NPC
ในส่วนนี้ฉันจะแนะนำปัญหา NPC ที่มีชื่อเสียงสามประการและอธิบายอัลกอริทึมการประมาณเพื่อเข้าหาพวกเขา
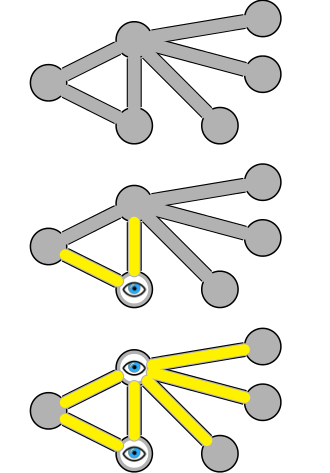
ความคิดหลัก ๆ
มันยากมากที่จะหาปกจุดสุดยอดขั้นต่ำ แต่เราสามารถหาฝาครอบโดยประมาณได้มากที่สุดสองเท่าของจุดยอดในเวลาพหุนาม

คุณสมบัติ
Back to Top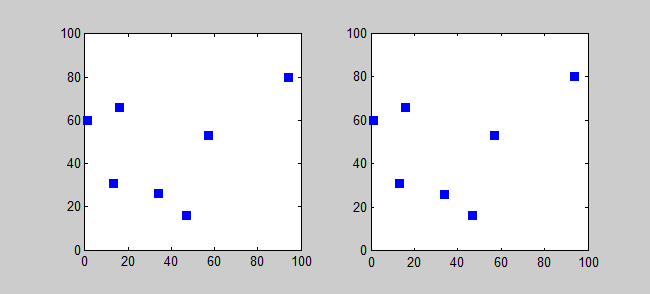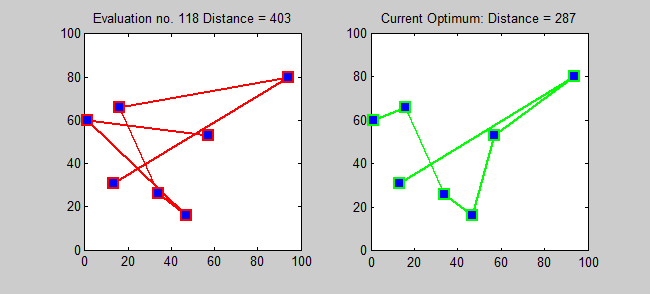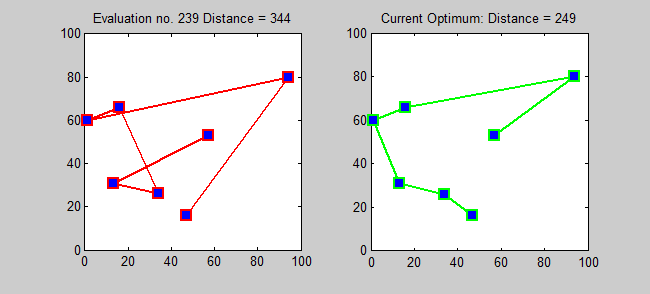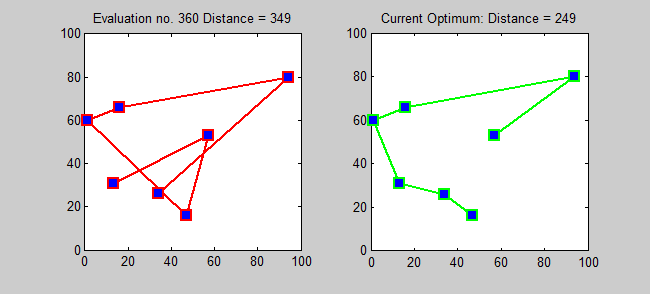
ความคิดหลัก ๆ
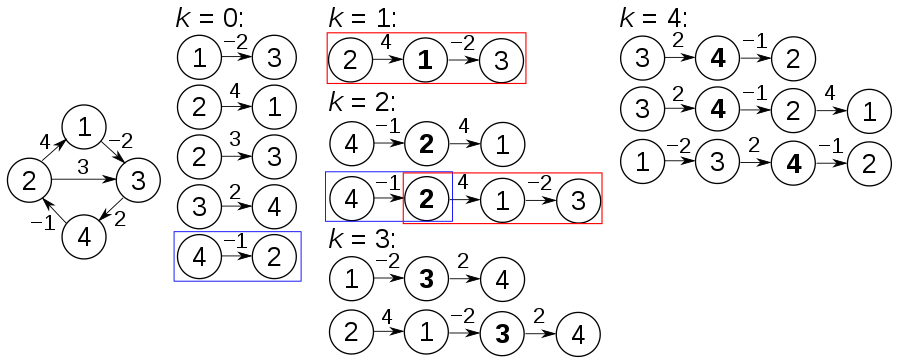
อัลกอริทึมการประมาณสำหรับ TSP เป็นอัลกอริทึมโลภ (CLRS P1114) ที่นี่ฉันต้องการแนะนำ อัลกอริทึมที่แน่นอน สำหรับ TSP โดยใช้การเขียนโปรแกรมแบบไดนามิก
subproblem: สำหรับทุกปลายทาง j ∈ {1,2, ... , n}, ชุดย่อยทุกชุด s ⊆ {1,2, ... , n} ที่มี 1 และ j, ให้ ls, j = ความยาวขั้นต่ำของเส้นทางจาก 1 ถึง J ดังนั้นการเกิดซ้ำที่สอดคล้องกัน:
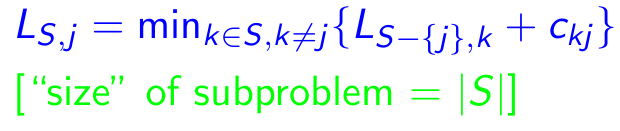
คุณสมบัติ
Back to Top 3-SAT เป็นหนึ่งในปัญหา 21 NP ที่สมบูรณ์ของ Karp และใช้เป็นจุดเริ่มต้นสำหรับการพิสูจน์ว่าปัญหาอื่น ๆ นั้นเป็น NP-hard
ในที่นี้ฉันแนะนำอัลกอริทึมของ Papadimitriou สำหรับ 2-Sat (นี่เป็น อัลกอริทึมที่น่าสนใจมาก ดังนั้นฉันจึงตัดสินใจที่จะแนะนำแม้ว่า 2-SAT ไม่ใช่ NPC)
ความคิดหลัก ๆ
เลือกการมอบหมายเริ่มต้นแบบสุ่มและเลือกประโยคที่ไม่พอใจโดยพลการและพลิกค่าของตัวแปรใดตัวหนึ่ง นี่คือ pseudocode:

การจัดการแบบสบาย ๆ เช่นนี้จะทำให้เรามีความน่าจะเป็นที่ใหญ่มากในการค้นหาคำตอบที่แท้จริง กลไกอยู่ในระยะฟิสิกส์ (การเดินแบบสุ่ม) หากคุณสนใจฉันขอแนะนำให้คุณผ่านการเดินแบบสุ่มที่เกี่ยวข้องกับ papadimitriou
คุณสมบัติ
Back to Top