algorithms in python

algoritmos en python

Este repositorio, usaré Python para implementar algunos algoritmos famosos. Los algoritmos se organizan de acuerdo con la estrategia utilizada. Cada algoritmo tendrá una explicación del problema que intenta resolver y algunos recursos relevantes.
(El objetivo de este repositorio es crear una hermosa lectura para todos estos algoritmos brillantes que he revisado).

Contenido:

• 1.0 - Divide y conquistar
  • 1.1 - Problema de multiplicación entre trabajos
  • 1.2 - Sorteo de fusión (y clasificación de inserción)
  • 1.3 - Conte las inversiones
  • 1.4 - Subarrray máxima
• 2.0 - Algoritmos aleatorios
  • 2.1 - clasificación rápida
  • 2.2 - Algoritmo de Karger
• 3.0 - Estructuras de datos
  • 3.1 - cola y amplitud primera búsqueda
  • 3.2 - Primera búsqueda de pila y profundidad
  • 3.3 - Mantenimiento medio y mediano
  • 3.4 - componente fuertemente conectado
  • 3.5 - Set de disjunto y SCC
• 4.0 - Algoritmos codiciosos
  • 4.1 - Actividades de cobertura
  • 4.2 - Selección de actividad
  • 4.3 - Codificación de Huffman
  • 4.4 - Algoritmo de Dijkstra
  • 4.5 - Algoritmo de Prim
  • 4.6 - El algoritmo de Kruskal y el problema de la agrupación
• 5.0 - Programación dinámica
  • 5.1 - Corte de barras
  • 5.2 - Multiplicación de la cadena de matriz
  • 5.3 - Subsecuencia común más larga
  • 5.4 - Algoritmo Floyd -Warshall
• 6.0 - Algoritmos de aproximación para NPC
  • 6.1 - Cubierta de vértices
  • 6.2 - Problema de vendedor ambulante
  • 6.3 - Problema de satisfilidad booleana

1.0 - Divide y conquistar

Esta sección, hablaré sobre la famosa estrategia de división y conquista y mostraré algunas aplicaciones de esta estrategia.

1.1 - Problema de multiplicación entre trabajos

• Enlace útil
  

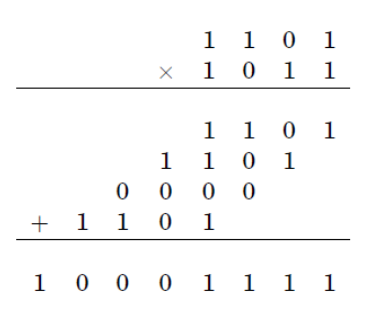
El procedimiento estándar para la multiplicación de dos números de N-dígitos requiere una serie de operaciones elementales proporcionales a. En cuanto al algoritmo Karatsuba, reduce el tiempo de ejecución a la mayoría

Idea clave
El paso básico del algoritmo de Karatsuba es una fórmula que le permite calcular el producto de dos grandes números y usar tres multiplicaciones de números más pequeños, cada uno con aproximadamente la mitad de dígitos que o, además de algunas adiciones y cambios de dígitos.
Propiedades

• Tiempo de ejecución:
  Back to Top

1.2 - Sorteo de fusión (y clasificación de inserción)

• Enlace útil
  Antes de discutir la clasificación de fusión, se analizará el algoritmo de clasificación de inserción y su tiempo de ejecución para apreciar la clasificación de fusiones. La imagen a continuación muestra que la idea intuitiva para la clasificación es imitar cómo las tarjetas se organizan de acuerdo con su tamaño. Cuando recibimos una tarjeta, la organizamos inmediatamente en función de otras tarjetas en nuestra mano.

El peor tiempo de ejecución para este algoritmo es.
GIF anterior muestra cómo funciona la clasificación de fusión: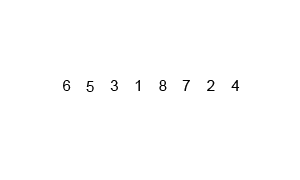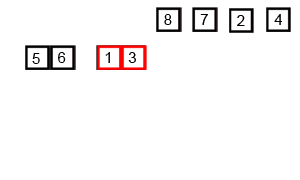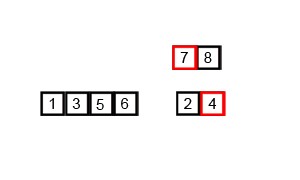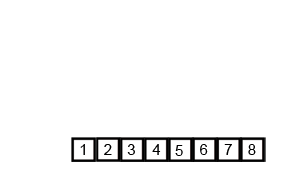

Idea clave
Divida la lista no organizada en n sublistas, cada uno que contiene 1 elemento (una lista de 1 elemento se considera ordenada) y fusione repetidamente sublistas para producir nuevos sublistas clasificados hasta que solo quede 1 sublista restante. Esta será la lista ordenada.
Propiedades

• Tiempo de ejecución:
  Back to Top

1.3 - Conte las inversiones

• Enlace útil
  En realidad, esto puede tratarse como la aplicación del orden de fusión. Cada vez que fusionamos la operación en el tipo de fusión, calculamos implícitamente las inversiones.
  

Idea clave
Al igual que la figura anterior, cuando primero tomamos un elemento desde la sub-array de la derecha en la operación de fusión, eso indica que el elemento derecho es más pequeño que (longitud de la sub-matriz izquierda-el índice del elemento izquierdo).
A medida que avanza el algoritmo, agregue todas las inversiones nos darán las inversiones totales.
Propiedades

• Tiempo de ejecución:
  Back to Top

1.4 - Subarrray máxima

• Enlace útil
  El problema máximo de la subarray es la tarea de encontrar la subarrray contigua dentro de una matriz unidimensional, a [1 ... n], de números que tienen la suma más grande.
  Idea clave
  Si usamos la estrategia de división y conquistar, si la matriz es un [bajo..migh] y el punto medio se representa como medio. A [i..j] es lo que queremos calcular. A [i..j] tiene que ser uno de los tres casos:
  

• A [i..j] pertenece a un [bajo..mid]
• A [i..j] pertenece a un [Mid+1..high]
• i <= Mid <j
  Por lo tanto, nuestro trabajo es encontrar la subgrora más grande que cruza el punto medio y elegir el más grande entre estos tres algoritmos.

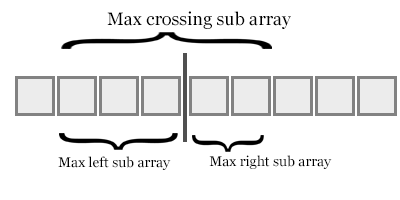
Propiedades

• Tiempo de ejecución:
  Back to Top

2.0 - Algoritmos aleatorios

Esta sección hablaré sobre dos algoritmos que han usado variable aleatoria en el interior.

2.1 - clasificación rápida

• Enlace útil
  

Idea clave
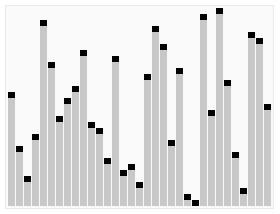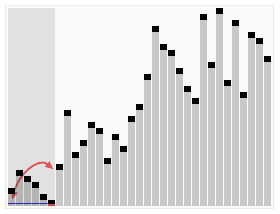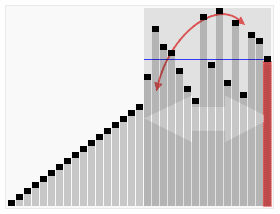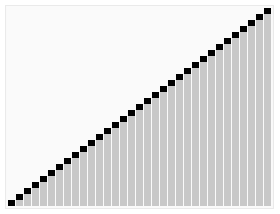
Quicksort primero divide una gran matriz en dos sub-matrices más pequeñas: los elementos bajos y los elementos altos en relación con un elemento elegido al azar. Quicksort puede ordenar recursivamente las subrayas. Entonces, el punto de clave en el tipo rápido es elegir el elemento de partición.
Propiedades

• El peor de los casos de rendimiento o (n^2)
• El mejor rendimiento de los casos o (n log n) o o (n) con partición de tres vías
• Rendimiento promedio de casos o (n log n)
  Back to Top

2.2 - Algoritmo Karger

• Enlace útil
  La idea del algoritmo se basa en el concepto de contracción de un borde (U, V) en un gráfico no dirigido G = (V, E). Hablando informalmente, la contracción de un borde fusiona los nodos U y V en uno, reduciendo el número total de nodos del gráfico por uno. La siguiente figura muestra cómo funciona la contracción. En la sub figura izquierda, dos nodos negros en negrita se fusionan en uno (la sub figura en la derecha).

Idea clave
Al repetir los tiempos del algoritmo de contracción con opciones aleatorias independientes y devolver el corte más pequeño, la probabilidad de no encontrar un corte mínimo es
Propiedades

• Con alta probabilidad, podemos encontrar todos los cortes min en el tiempo de ejecución de
• No encontrar una probabilidad de corte mínimo son tiempos.
  Back to Top

3.0 - Estructuras de datos

Colocar estructuras de datos como una sección independiente es engañoso; Sin embargo, introduciré problemas desconcertantes que se resuelven elegantemente por las estructuras de datos. Algunas estructuras de datos pueden tener una estrategia de diseño de algoritmo que aún no se ha revisado.

3.1 - cola y amplitud primera búsqueda

• Link1 de enlace útil22
  La cola, también conocida como FIFO, es un acrónimo de First In, First Out, un método para organizar y manipular un búfer de datos, donde la entrada más antigua (primera), o 'cabeza' de la cola, se procesa primero.

Idea clave
BFS se utiliza para contar nodos accesibles desde un nodo fuente en un gráfico no dirigido o dirigido. Los nodos accesibles se imprimen en el orden encontrado. Se usa una cola para almacenar los nodos de color gris (ver el GIF a continuación). El término "amplitud" en BFS significa encontrar un nodo accesible con la longitud más corta. La amplitud extiende el borde entre los nodos visitados y los nodos no descubiertos.

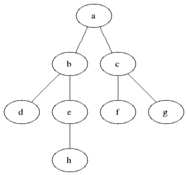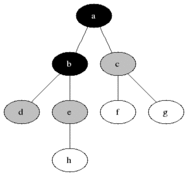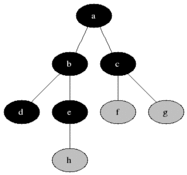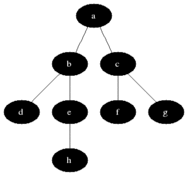
Propiedades

• Tiempo de ejecución: t (n) = o (v+e), v es número de vértices, e es un número de bordes
  Back to Top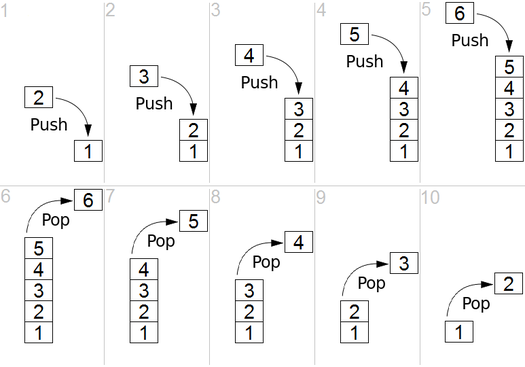

3.2 - Primera búsqueda de pila y profundidad

• Link1 de enlace útil22
  Stack, también conocido como LIFO, tiene la propiedad de Last In, First Out.
  

Idea clave
Y DFS se usa en el gráfico dirigido y dice cuántos nodos puede alcanzar un nodo fuente e imprimirlos por el orden que los encontramos. Usamos Stack para almacenar los nodos que clasificamos como puntos de inicio para el gráfico. La "profundidad" en su nombre significa que este algoritmo irá tan profundamente como sea posible para una fuente dada y cuando alcance el punto final, vuelve al nodo de inicio.

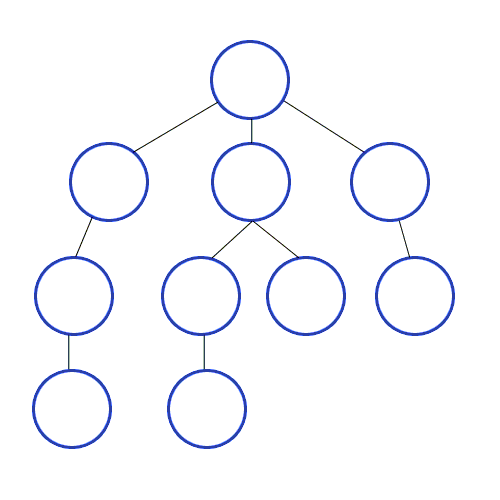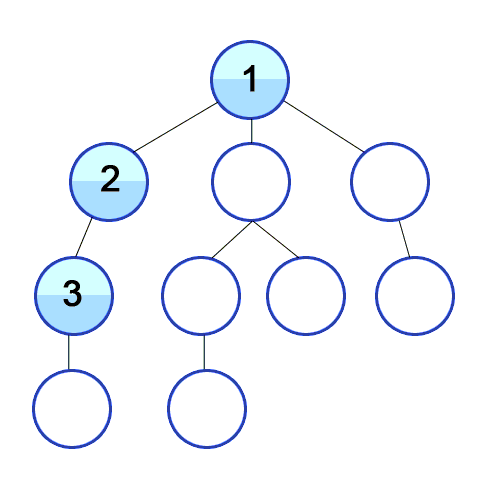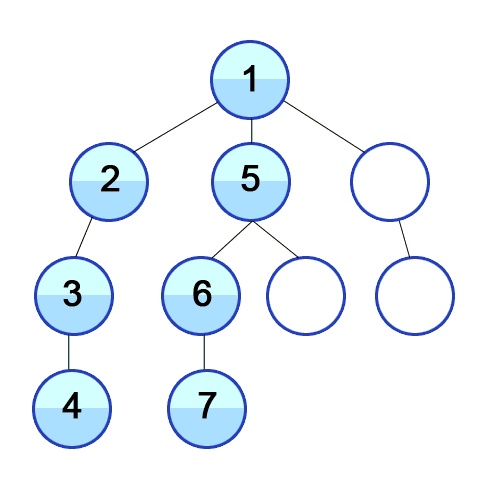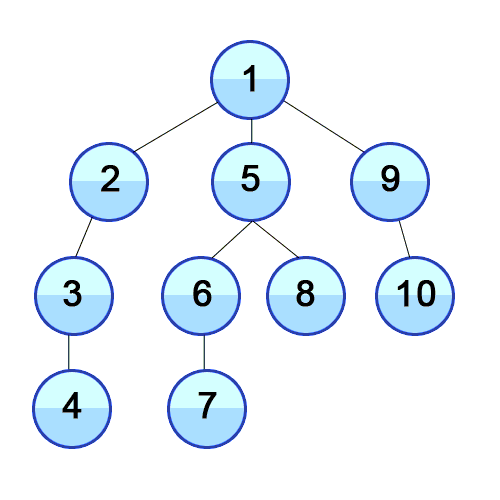
Propiedades

• Tiempo de ejecución: t (n) = o (v+e), v es número de vértices, e es un número de bordes
  Back to Top

3.3 - Mantenimiento medio y mediano

• Link1 de enlace útil22
  Heap es una estructura de datos especializada basada en árbol que satisface la propiedad del montón: si P es un nodo principal de C, entonces la clave (el valor) de P es mayor o igual a (en un montón máximo) o menos o igual a (en un montón mínimo) la clave de C. [1] El nodo en la "parte superior" del montón (sin padres) se llama nodo raíz.

El problema mediano de mantenimiento es que si se leen enteros de un flujo de datos, encuentre una mediana de elementos leídos de manera eficiente. Por simplicidad, suponga que no hay duplicados.

Idea clave
Podemos usar un montón máximo en el lado izquierdo para representar elementos que son menos que la mediana efectiva, y un montón mínimo en el lado derecho para representar elementos que son mayores que la mediana efectiva. Cuando la diferencia entre el tamaño de dos montones es mayor o igual a 2, cambiamos un elemento a otro montón de tamaño más pequeño.

Propiedades

• Tiempo de ejecución:
  Back to Top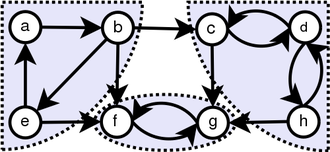

3.4 - componente fuertemente conectado

• Enlace útil
  Un gráfico dirigido se llama fuertemente conectado si hay una ruta en cada dirección entre cada par de vértices del gráfico. En un gráfico dirigido G que puede no estar fuertemente conectado, se dice que un par de vértices U y V están fuertemente conectados entre sí si hay una ruta en cada dirección entre ellos.

Idea clave
A través de una simple observación, descubrimos que Tranpose of Graph tiene el mismo SCC que el gráfico original. Ejecutamos DFS dos veces. La primera vez, lo ejecutamos en G y calculamos el tiempo de finalización para cada vértice. Y luego, ejecutamos DFS en G^t pero en el bucle principal de DFS, considere los vértices en orden de disminución del tiempo de finalización.
Propiedades

• Tiempo de ejecución: v es número de vértices, e es un número de bordes
  Back to Top

3.5 - Set de disjunto y SCC

• Enlace útil
  Una estructura de datos de conjunto de disjunto, también llamada estructura de datos de unión o un conjunto de fusiones de fusión, es una estructura de datos que realiza un seguimiento de un conjunto de elementos divididos en una serie de subconjuntos disjuntos (no superpuestas).
  Para un set de disjunta ingenuo, admite dos operaciones principales, maquillaje y unión. Make-Set hace que cada vértice sea un grupo independiente. Union pone dos vértices en un grupo.

Idea clave
En un gráfico no dirigido, podemos usar esta estructura de datos para averiguar cuántos SCC. La siguiente figura muestra cómo funciona.

Propiedades

• Podemos usar una heurística de unión ponderada para ahorrar tiempo cuando la operación Find_set llame
• La compresión de la ruta puede mejorar en gran medida la eficiencia del tiempo de la Unión.
  Back to Top

4.0 - Algoritmos codiciosos

En esta sección, voy a introducir algoritmos codiciosos, una poderosa estrategia de diseño de algoritmos.
Desde Wikipedia, un algoritmo codicioso es un paradigma algorítmico que sigue a los problemas que resuelven la heurística de hacer la decisión localmente óptima en cada etapa [1] con la esperanza de encontrar un óptimo global. En muchos problemas, una estrategia codiciosa no produce en general una solución óptima, pero, sin embargo, una heurística codiciosa puede producir soluciones localmente óptimas que se aproximan a una solución óptima global en un tiempo razonable.

4.1 - Actividades de cobertura

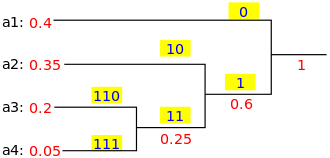
En el problema de selección de actividades, cada actividad tiene su propio peso y longitud. Y nuestro objetivo es minimizar la suma de peso*longitud. Es un ejemplo muy fácil y excelente para mostrar cómo funciona el algoritmo codicioso y proporcionar una prueba elegante utilizando la técnica de intercambio de argumentos.
Idea clave
Si clasificamos la actividad por peso/longitud, podemos demostrar que una estructura óptima existente no puede ser mejor que esta disposición.

Como la figura mostrada anteriormente, consideramos el costo causado por dos actividades que varían de manera diferente en dos disposiciones (I, J). Descubrimos que el costo en el algoritmo codicioso es más pequeño que la estructura óptima por el valor de wi*lj - wj*li, que es mayor o igual a 0.

Propiedades

• El tiempo de ejecución está dominado por la clasificación
  Back to Top

4.2 - Selección de actividad

• Enlace útil
  En este problema, cada actividad tiene su propio tiempo de inicio y tiempo de finalización. Nuestro objetivo es seleccionar un subconjunto de longitud máxima, donde los trabajos son compatibles.
  

Idea clave
Ordenamos la matriz de acuerdo con su tiempo de finalización. El algoritmo puso el primer trabajo cuyo tiempo de inicio es más grande que el tiempo de finalización del último trabajo.
Propiedades

• El tiempo de ejecución de la selección de actividad recursiva es
  Back to Top

4.3 - Codificación de Huffman

• Enlace útil
  El código Huffman es un tipo particular de código de prefijo óptimo que se usa comúnmente para la compresión de datos sin pérdidas. Por ejemplo, la siguiente tabla muestra la frecuencia de las letras en un "libro".

Una forma de codificar este libro es usar la codificación de longitud fija. Como se muestra a continuación:

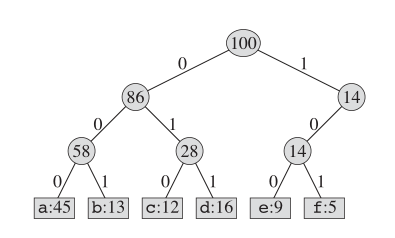
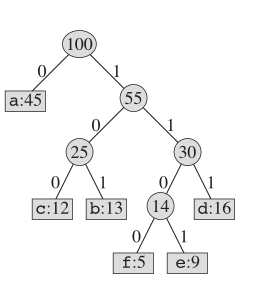
En cuanto a la codificación de Huffman, la estructura real del árbol se ve así:

Idea clave
Mantenemos un árbol binario y creamos un nuevo nodo como padre para dos letras menos frecuentes. Y la clave para este nuevo nodo es la suma de claves para sus dos hijos. Repetimos esto hasta que no queden nodos en este "libro".

Propiedades

• Procedimiento Huffman produce un código de prefijo óptimo
  Back to Top

4.4 - Algoritmo de Dijkstra

• Enlace útil
  

El algoritmo de Dijkstra es un algoritmo para encontrar las rutas más cortas entre los nodos en un gráfico. Sin embargo, tiene un requisito previo, todas las rutas deben ser mayores o iguales a 0.

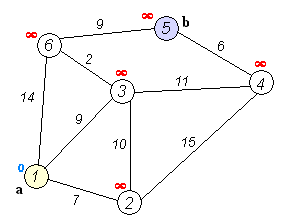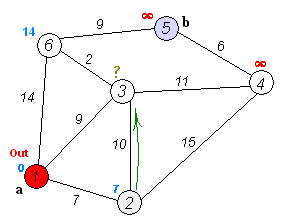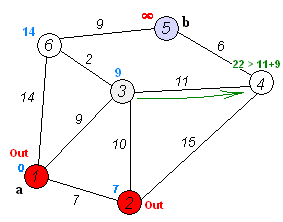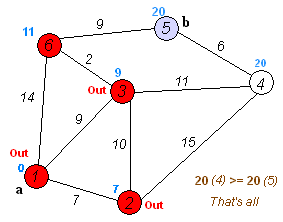
Idea clave
Nodos separados en dos grupos, un grupo está marcado como se explora. Y actualizamos la distancia desde el grupo inexplorado hasta el grupo explorado por la distancia más corta.

Propiedades

• Tiempo de ejecución basado en una cola de prioridad mínima implementada por un montón de Fibonacci
  Back to Top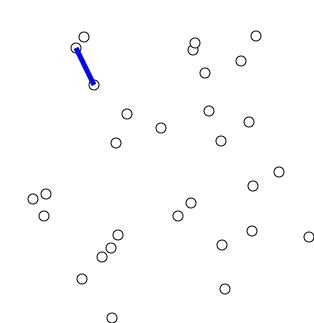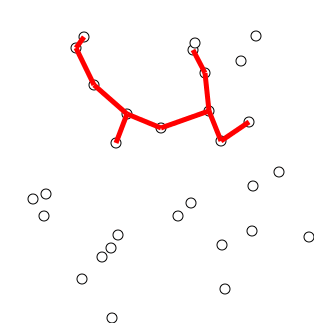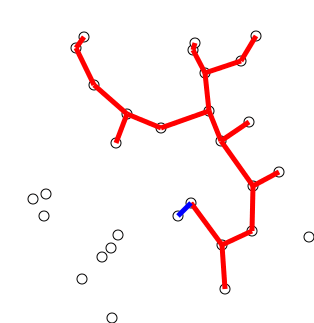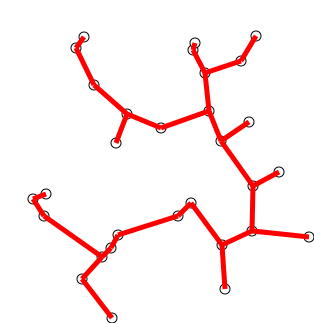

4.5 - Algoritmo Prim

• Enlace útil
  El algoritmo de Prim es un algoritmo codicioso que encuentra un árbol de expansión mínimo para un gráfico no dirigido ponderado. Muy similar al algoritmo de Dijkstra, mantenemos dos conjuntos, exploramos uno y inexplorado uno. Cada vez, solo absorbemos el vértice, que tiene la distancia más pequeña al conjunto explorado. Esto se muestra muy claramente en la figura a continuación:

Idea clave
El algoritmo puede describirse informalmente como realizando los siguientes pasos:

Inicialice un árbol con un solo vértice, elegido arbitrariamente del gráfico.
Cultive el árbol por un borde: de los bordes que conectan el árbol a los vértices que aún no están en el árbol, encuentre el borde de peso mínimo y transfiéralos al árbol.
Repita el paso 2 (hasta que todos los vértices estén en el árbol).

Propiedades

• Tiempo de ejecución

• matriz de adyacencia, búsqueda
• Lista de moneda binaria y adyacencia
• Fibonacci montón y lista de adyacencia
  Back to Top

4.6 - Algoritmo de Kruskal y problema de agrupación

• Enlace útil
  El algoritmo de Prim es otro algoritmo codicioso que encuentra un árbol de expansión mínimo para un gráfico no dirigido ponderado. En lugar de mantener un árbol como Prim, mantiene el bosque.

Idea clave
Muy similar a SCC, podemos detener temprano el algritmo para controlar el número de clases en nuestro gráfico, lo que quiere decir que podemos agrupar el gráfico.

Propiedades

• Tiempo de ejecución o (elogv)
  Back to Top

5.0 - Programación dinámica

En esta sección, voy a introducir algoritmos dinámicos, una poderosa estrategia de diseño de algoritmos.
Desde Wikipedia, la programación dinámica (también conocida como optimización dinámica) es un método para resolver un problema complejo al dividirlo en una colección de subproblemas más simples, resolver cada uno de esos subproblemas solo una vez y almacenar sus soluciones.

5.1 - Corte de barras

• Enlace útil
  Dada una varilla de longitud n pulgadas y una variedad de precios que contienen precios de todas las piezas de tamaño más pequeñas que n. Determine el valor máximo que se puede obtener cortando la barra y vendiendo las piezas.
  La siguiente tabla muestra la relación entre el precio y la longitud.

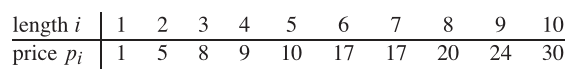
Entonces, si la longitud de la barra es 8 y los valores de diferentes piezas se dan de la siguiente manera, entonces el valor máximo obtenible es 22 (cortando dos piezas de longitudes 2 y 6).

Idea clave
Vemos que una descomposición consiste en una primera pieza de longitud que corté el extremo izquierdo, y luego un resto de la longitud a la derecha n-i. Entonces, el pseudocodo parece:

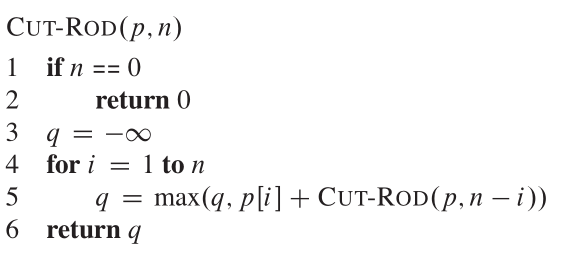
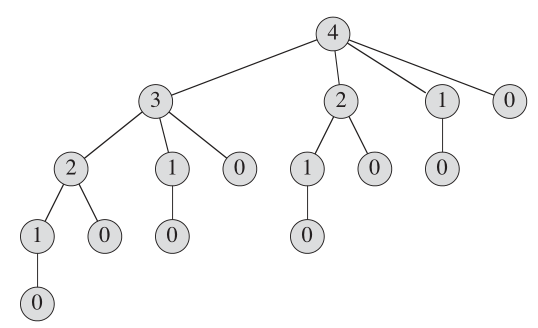
El árbol de recursión que muestra llamadas recursivas resultantes de una llamada Cut_rod (P, N) parece:

Para guardar el cálculo repetido para pequeños subproblemas, memorizamos una matriz para almacenar estos valores.

Propiedades

• La complejidad del tiempo de la implementación anterior es O (n^2)
  Back to Top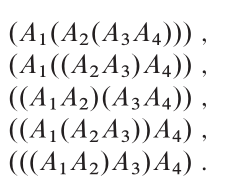

5.2 - Multiplicación de la cadena de matriz

• Enlace útil
  La multiplicación de la cadena de matriz (o problema de ordenamiento de cadena de matriz, MCOP) es un problema de optimización que se puede resolver utilizando la programación dinámica. Dada una secuencia de matrices, el objetivo es encontrar la forma más eficiente de multiplicar estas matrices. El problema no es realmente realizar las multiplicaciones, sino simplemente decidir la secuencia de las multiplicaciones de matriz involucradas.

Idea clave
Estructura óptima:

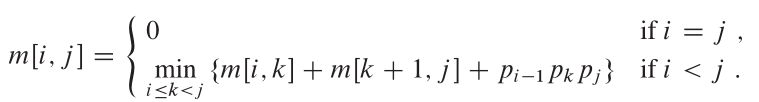
Propiedades

• La complejidad del tiempo de la implementación anterior es
  Back to Top

5.3 - Subsecuencia común más larga

• Enlace útil
  El problema más largo de la subsecuencia común (LCS) es el problema de encontrar la posterior posterior más larga común a todas las secuencias en un conjunto de secuencias (a menudo solo dos secuencias).

Idea clave
De CLRS, la estructura óptima para este problema es:

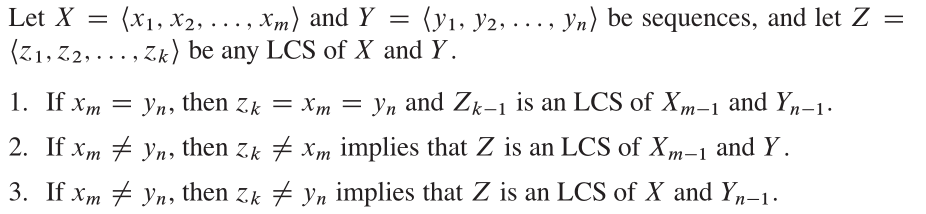
Propiedades

• La complejidad del tiempo de la implementación anterior es $ theta (mn) $
  Back to Top

5.4 - Algoritmo Floyd -Warshall

• Enlace útil
  El algoritmo Floyd -Warshall es un algoritmo para encontrar rutas más cortas en un gráfico ponderado con pesos de borde positivos o negativos (pero sin ciclos negativos).

Idea clave
Este algoritmo se basa en una observación muy intuitiva. Supongamos que tenemos un subconjunto {1, 2, 3, 4, ..., k} (denote como v (k)) del grupo de vértices originales {1, 2, 3, ..., n}. Si P es un camino más corto de I a J en V (K), tenemos dos casos. Primero, si K no está en P, P debe ser una ruta más corta en V (K-1). Segundo, si K está en P, entonces podemos separar el camino en dos, P1: I K, P2: K j. y P1 debe ser el camino más corto de I a K con V (K-1), P2 debe ser el camino más corto de K a J con V (K-1).

Propiedades

• La complejidad del tiempo de la implementación anterior es
  Back to Top

6.0 - Algoritmos de aproximación para NPC

Desde Wikipedia, un problema de decisión NP-completado es uno que pertenece tanto a las clases de complejidad NP y NP-Hard. En este contexto, NP significa "tiempo polinomial no determinista". El conjunto de problemas completos de NP a menudo se denota por NP-C o NPC.

En esta sección, voy a presentar tres problemas de NPC muy famosos y explicar los algoritmos de aproximación para abordarlos.

6.1 - Cubierta de vértices

• Enlace útil
  Una cubierta de vértice (a veces la cubierta del nodo) de un gráfico es un conjunto de vértices, de modo que cada borde del gráfico es incidente a al menos un vértice del conjunto. La siguiente figura muestra una cubierta mínima del vértice (donde el conjunto de cubierta debe tener al menos dos vértices, cero y una no ayudaría).

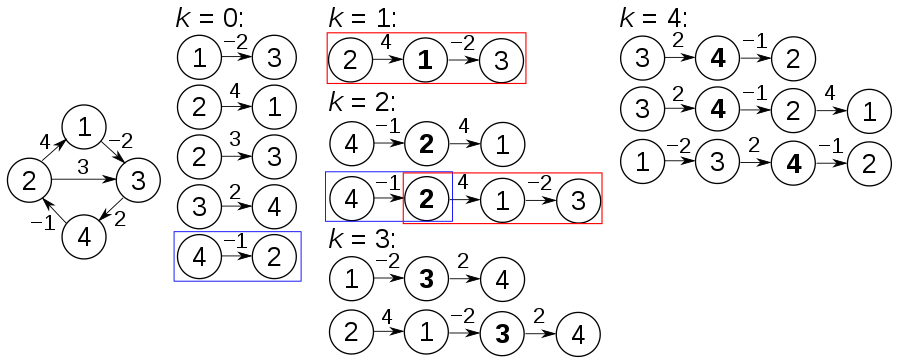
Idea clave
Es muy difícil encontrar una cubierta mínima de vértice, pero podemos encontrar una cubierta aproximada con el máximo el doble de los vértices en tiempo polinomial.

Propiedades

• La cobertura de Apror-Viex es un algoritmo de Aprolitación de 2 tiempos polinómicos.
  Back to Top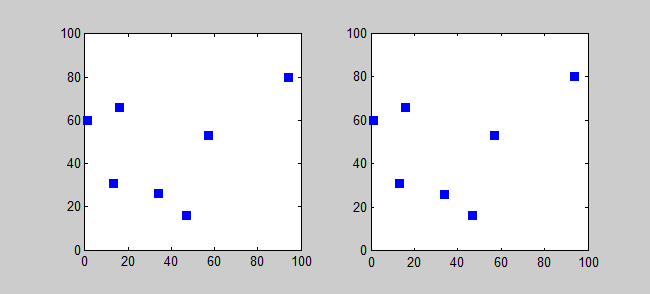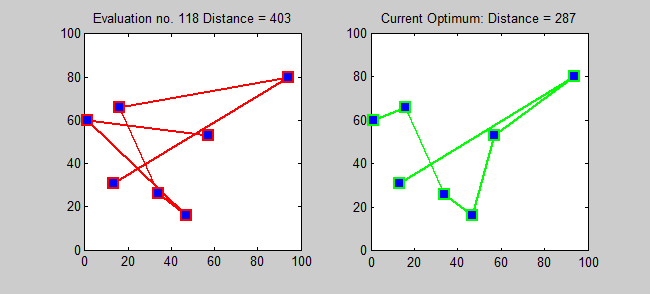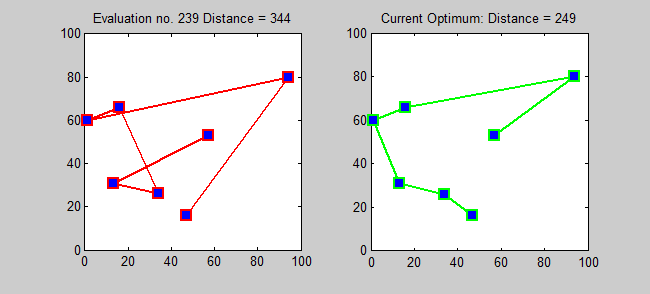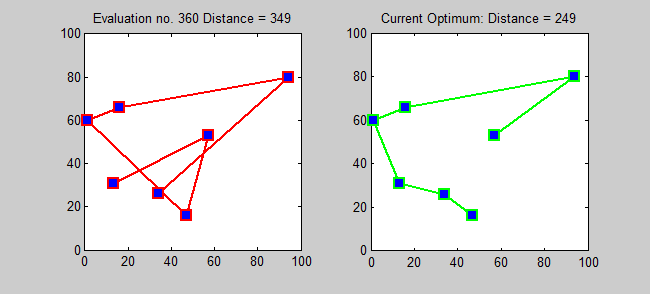

6.2 - Problema de vendedor ambulante

• Enlace útil
  El problema del vendedor ambulante (TSP) hace la siguiente pregunta: "Dada una lista de ciudades y las distancias entre cada par de ciudades, ¿cuál es la ruta más corta posible que visita cada ciudad y regresa a la ciudad de Origin?" El GIF muestra la fuerza bruta para TSP.

Idea clave
El algoritmo de aproximación para TSP es un algoritmo codicioso (CLRS P1114). Aquí, también quiero introducir un algoritmo exacto para TSP utilizando programación dinámica.

Subproblema: para cada destino j ∈ {1,2, ..., n}, cada subconjunto s ⊆ {1,2, ..., n} que contiene 1 y j, que Ls, j = longitud mínima de una ruta de 1 a j que visite precisamente los vértices de S [exactamente una vez cada uno]. Entonces, la recurrencia correspondiente:

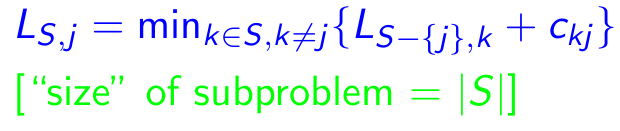
Propiedades

• Tiempo de ejecución para algoritmo exacto:
  Back to Top

6.3 - Problema de satisfilidad booleana

• Enlace útil
  El problema de satisfilidad booleano (a veces llamado problema de satisfacción proposicional y abreviado como satisfilidad o SAT) es el problema de determinar si existe una interpretación que satisface una fórmula booleana dada.

3-SAT es uno de los 21 problemas completos de KARP NP, y se utiliza como punto de partida para demostrar que otros problemas también son np.

Aquí, presento el algoritmo de Papadimitriou para 2-sat (este es un algoritmo muy muy interesante , por lo que decido presentarlo a pesar de que 2-SAT no es NPC).

Idea clave
Elija una asignación inicial aleatoria y elija una cláusula arbitraria insatisfecha arbitraria y voltee el valor de una de sus variables. Aquí está el pseudocódigo:

Un trato casual con cláusulas nos daría una probabilidad muy grande de encontrar la respuesta real. El mecanismo se encuentra en un término físico (caminata aleatoria). Si está interesado, le recomiendo que pase por cómo la caminata aleatoria se relacionó con Papadimitriou.

Propiedades

• Para una instancia de 2-SAT satisfable con N variables, el algoritmo de Papadimitriou produce una asignación satisfactoria con probabilidad ≥ 1-1/n
• Corre en tiempo polinomial
• Siempre correcto en instancias insatisfactorias
  Back to Top