SQL Server正態分佈,高斯或鐘形曲線
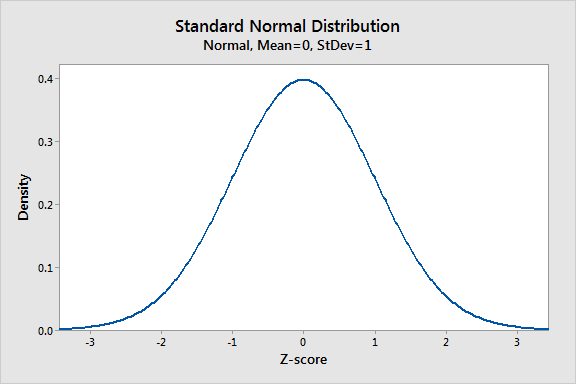
正態分佈是統計中最重要的概率分佈,因為它符合許多自然現象。例如,高度,血壓,測量誤差和智商得分遵循正態分佈。它也被稱為高斯分佈和鍾形曲線。
正態分佈是描述變量值分佈的概率函數。這是一個對稱分佈,其中大多數觀測值都集中在中心峰周圍,並且在兩個方向上平均錐度均勻偏離平均錐度的值概率。分佈的兩個尾巴中的極端值也不太可能。
在此博客文章中,您將學習如何使用正常分佈,其參數以及如何計算z得分以標準化數據並找到概率。正態分佈數據的示例:高度
高度數據是正態分佈的。此示例中的分佈符合我在研究期間從14歲女孩那裡收集的真實數據。
高度的正態分佈。
如您所見,高度的分佈遵循所有正常分佈的典型模式。大多數女孩接近平均水平(1.512米)。一個人的身高和平均值之間的差異小於與平均值的實質性偏差。標準偏差為0.0741m,這表明單個女孩往往會從平均身高下降的典型距離。
分佈是對稱的。女子的人數短於平均水平,等於高於平均水平的女孩人數。在分佈的兩個尾巴中,極度短的女孩的出現很少像極高的女孩一樣。正態分佈的參數
與任何概率分佈一樣,正態分佈的參數完全定義其形狀和概率。正態分佈具有兩個參數,平均值和標準偏差。正態分佈不僅具有一種形式。相反,形狀基於參數值會更改,如下圖所示。意思是
平均值是分佈的核心趨勢。它定義了正常分佈的峰位置。大多數值集中在均值周圍。在圖上,更改均值將整個曲線移動在X軸上向左或向右移動。
以不同方式顯示正常分佈的圖。標準偏差
標準偏差是可變性的度量。它定義了正態分佈的寬度。標準偏差決定了距離平均值往往會下降多遠。它代表觀測值和平均值之間的典型距離。
在圖表上,更改標準偏差可以收緊或沿X軸分佈的寬度。較大的標準偏差會產生更分佈的分佈。
圖表顯示出具有不同標準偏差的正常分佈。
當您的分佈狹窄時,概率較高,即值不會遠離平均值。隨著您增加分佈的傳播,觀察結果遠離平均值的可能性也會增加。人口參數與樣本估計值
平均值和標準偏差是適用於整個人群的參數值。對於正態分佈,統計學家通過使用希臘符號μ(MU)來表示參數,用於種群平均值,σ(Sigma)用於人口標準偏差。
不幸的是,人口參數通常是未知的,因為通常不可能衡量整個人口。但是,您可以使用隨機樣本來計算這些參數的估計值。統計學家代表這些參數的樣本估計值,用於樣品平均值和样本標準偏差的樣本均值。
相關文章:正態分佈的各種形式的中心趨勢和可變性的衡量標準
儘管形狀不同,但所有形式的正態分佈都具有以下特徵性能。
They’re all symmetric. The normal distribution cannot model skewed distributions.
The mean, median, and mode are all equal.
Half of the population is less than the mean and half is greater than the mean.
The Empirical Rule allows you to determine the proportion of values that fall within certain distances from the mean. More on this below!
儘管正態分佈在統計中至關重要,但它只是許多概率分佈之一,並且不符合所有種群。要了解如何確定正態分佈是否為您的樣本數據提供最佳擬合,請閱讀有關如何識別數據分佈並評估正態性的文章:直方圖與正常概率圖。正態分佈的經驗規則
當您正常分佈數據時,標準偏差將變得特別有價值。您可以使用它來確定屬於指定數量的標準偏差與平均值的值的比例。例如,在正態分佈中,有68%的觀測值屬於+/- 1與平均值的標準偏差。該屬性是經驗規則的一部分,該屬性描述了與鍾形曲線平均值的特定數量偏差數在特定的標準偏差之內的數據百分比。平均+/-標準偏差百分比包含1 68%2 95%3 99.7%
讓我們看一個披薩送貨示例。假設一家披薩餐廳的平均交貨時間為30分鐘,標準偏差為5分鐘。使用經驗規則,我們可以確定68%的輸送時間在25-35分鐘之間(30 +/- 5),95%在20-40分鐘之間(30 +/- 2 5),而99.7%在15-45分鐘之間(30 +/- 3 5)。下圖以圖形方式說明了此屬性。
圖表顯示正態分佈,區域除以標準偏差。標準正態分佈和標準分數
如上所述,正態分佈具有許多不同的形狀,具體取決於參數值。但是,標準正態分佈是平均值為零且標準偏差為1的正態分佈的特殊情況。此分佈也稱為z分佈。
標準正態分佈的值稱為標準分數或z得分。標準分數表示特定觀察值下降的平均值以上或低於平均值的標準偏差數量。例如,標準分數為1.5,表明該觀察值高於平均值1.5標準偏差。另一方面,負分數代表低於平均值的值。平均值為0。
圖表顯示標準正態分佈。
假設您稱重蘋果,重110克。從一個蘋果與其他蘋果相比,沒有辦法從重量中分辨出來。但是,如您所見,在計算其Z分數後,您知道它相對於其他蘋果的位置。標準化:如何計算z得分
標準分數是了解特定觀察結果相對於整個分佈的何處的好方法。它們還允許您從具有不同手段和標準偏差的正態分佈中提取的觀察結果,並將其放置在標準尺度上。該標準秤使您能夠比較原本很難的觀察結果。
此過程稱為標準化,它允許您比較觀察結果併計算不同人群的概率。換句話說,它允許您將蘋果與橘子進行比較。統計不大!
為了標準化數據,您需要將原始測量值轉換為Z分數。
要計算觀察的標準分數,請進行原始測量,減去平均值並除以標準偏差。從數學上講,該過程的公式如下:
z = { displaystyle frac { text {x} - mu} { sigma}}}}
x表示興趣測量的原始價值。 MU和Sigma代表了從中繪製觀測值的人群的參數。
標準化數據後,您可以將它們放置在標準正態分佈中。通過這種方式,標準化使您可以根據每個觀測值屬於其自身分佈的位置比較不同類型的觀測值。使用標準分數將蘋果進行橙色比較的示例
假設我們想將蘋果與橙子進行比較。具體來說,讓我們比較自己的體重。想像一下,我們有一個重110克的蘋果和一個重100克的橙色。
如果我們比較原始值,很容易看到蘋果的重量比橙色重。但是,讓我們比較他們的標準分數。為此,我們需要了解蘋果和橘子的重量分佈的屬性。假設蘋果和橙子的權重遵循正態分佈,其參數值以下:蘋果橙平均重量克100 140標準偏差15 25
現在,我們將計算Z分數:
Apple = 110-100/15 = 0.667
Orange = 100-140/25 = -1.6
蘋果的Z分數(0.667)為正,這意味著我們的蘋果的重量大於普通蘋果。無論如何,這都不是極端價值,但是蘋果的平均水平高於平均水平。另一方面,橙色的z得分相當負(-1.6)。它遠低於橘子的平均重量。我將這些Z值放在下面的標準正態分佈中。
使用z評分將蘋果與橙色進行比較的標準正態分佈圖。
雖然我們的蘋果的重量比橙色重,但我們的蘋果比平均蘋果更重的蘋果與徹頭徹尾的微弱的橙色進行了比較!使用Z分數,我們已經了解了每個果實如何適合其自身分佈以及它們如何相互比較。在正態分佈的曲線下查找區域
正態分佈是概率分佈。與任何概率分佈一樣,在概率分佈圖上屬於兩個點之間的曲線面積的比例表明值將值在該間隔內。要了解有關此屬性的更多信息,請閱讀我有關理解概率分佈的文章。
通常,我使用統計軟件來查找曲線下的區域。但是,當您使用正態分佈並將值轉換為標準分數時,您可以通過在標準正態分佈表中查找z得分來計算區域。
由於存在無限數量的不同正常分佈,因此發布者無法為每個分佈打印一張表。但是,您可以將值從任何正常分佈轉換為z得分,然後使用標準分數表來計算概率。使用z得分錶
讓我們對蘋果(0.667)進行Z分數,並使用它來確定其重量百分位。百分位數是人口的比例低於特定價值。因此,要確定百分位數,我們需要找到與小於0.667的Z分數範圍相對應的區域。在下表的部分中,我們最接近我們的z得分為0.65,我們將使用。
照片顯示了標準分數表(z得分)的一部分。
這些表的訣竅是將值與正態分佈的屬性結合使用來計算所需的概率。表值表明-0.65和+0.65之間的曲線面積為48.43%。但是,這不是我們想知道的。我們希望該區域小於Z得分為0.65。
我們知道正態分佈的兩個半分佈是彼此的鏡像。因此,如果間隔為-0.65和+0.65的區域為48.43%,則範圍從0到+0.65,必須是其中的一半:48.43/2 = 24.215%。此外,我們知道所有分數小於零的面積是分佈的一半(50%)。
因此,所有分數的面積高達0.65 = 50% + 24.215%= 74.215%
我們的蘋果大約是第74個百分位數。
以下是統計軟件產生的概率分佈圖,該圖顯示了相同的百分位數以及曲線下相應區域的圖形表示。該值略有不同,因為我們使用表格為0.65,而軟件則使用更精確的值為0.667。
使用Z分數以圖形方式顯示百分位數的概率分佈圖。正態分佈很重要的其他原因
除了上述所有內容外,正態分佈在統計數據中至關重要的其他原因有很多。
Some statistical hypothesis tests assume that the data follow a normal distribution. However, as I explain in my post about parametric and nonparametric tests, there’s more to it than only whether the data are normally distributed.
Linear and nonlinear regression both assume that the residuals follow a normal distribution. Learn more in my post about assessing residual plots.
The central limit theorem states that as the sample size increases, the sampling distribution of the mean follows a normal distribution even when the underlying distribution of the original variable is non-normal.
這是關於正態分佈的很多!希望您可以理解,這是至關重要的,因為分析師使用它的多種方式。
資料來源:https://statistissbyjim.com/basics/normal-distribution/

具有期望值0和標準偏差的正態分佈的累積概率1: 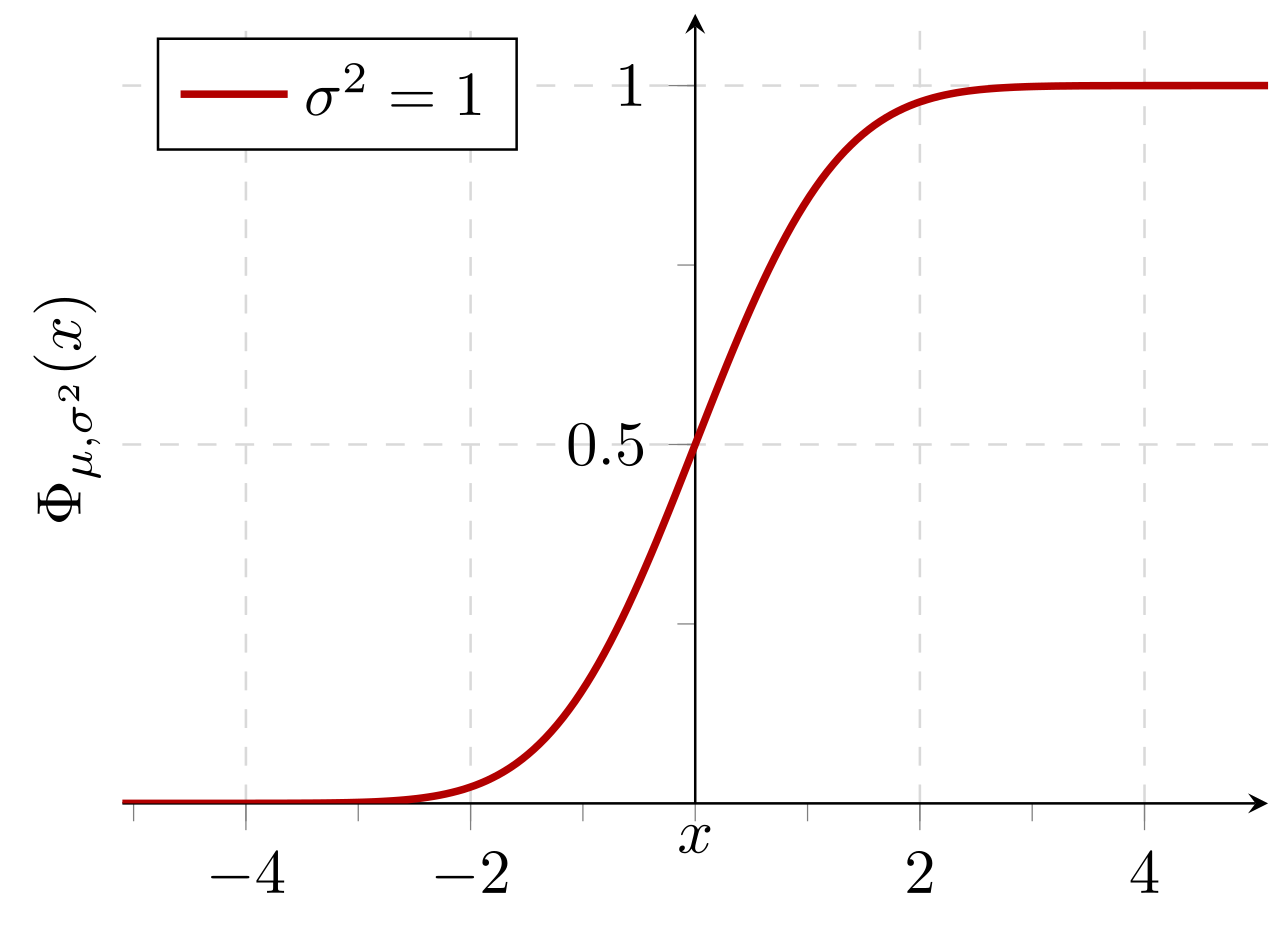
這是免費且無限制的軟件,發佈到公共領域 - 有關詳細信息,請參見許可證文件。
由JavierCañon製成的。