SQL Server Normal Distribution, Gauss o Bell Curve
La distribución normal es la distribución de probabilidad más importante en las estadísticas porque se ajusta a muchos fenómenos naturales. Por ejemplo, las alturas, la presión arterial, el error de medición y los puntajes de IQ siguen la distribución normal. También se conoce como la distribución gaussiana y la curva de campana.
La distribución normal es una función de probabilidad que describe cómo se distribuyen los valores de una variable. Es una distribución simétrica donde la mayoría de las observaciones se agrupan alrededor del pico central y las probabilidades de valores más lejos de la reducción media de la igualmente en ambas direcciones. Los valores extremos en ambas colas de la distribución son igualmente improbables.
En esta publicación de blog, aprenderá cómo usar la distribución normal, sus parámetros y cómo calcular las puntuaciones Z para estandarizar sus datos y encontrar probabilidades. Ejemplo de datos distribuidos normalmente: alturas
Los datos de altura se distribuyen normalmente. La distribución en este ejemplo se ajusta a los datos reales que recopilé de las niñas de 14 años durante un estudio.
Distribución normal de alturas.
Como puede ver, la distribución de alturas sigue el patrón típico para todas las distribuciones normales. La mayoría de las chicas están cerca del promedio (1.512 metros). Pequeñas diferencias entre la altura de un individuo y la media ocurren con mayor frecuencia que las desviaciones sustanciales de la media. La desviación estándar es 0.0741m, lo que indica la distancia típica de que las niñas individuales tienden a caer desde la altura media.
La distribución es simétrica. El número de chicas más cortas que el promedio es igual al número de niñas más alta que el promedio. En ambas colas de la distribución, las niñas extremadamente cortas ocurren tan con poca frecuencia como las niñas extremadamente altas. Parámetros de la distribución normal
Al igual que con cualquier distribución de probabilidad, los parámetros para la distribución normal definen su forma y probabilidades por completo. La distribución normal tiene dos parámetros, la media y la desviación estándar. La distribución normal no tiene una sola forma. En cambio, la forma cambia en función de los valores de los parámetros, como se muestra en los gráficos a continuación. Significar
La media es la tendencia central de la distribución. Define la ubicación del pico para distribuciones normales. La mayoría de los valores se agrupan alrededor de la media. En un gráfico, cambiar la media cambia toda la curva hacia la izquierda o hacia la derecha en el eje X.
Gráfico que muestre distribuciones normales con diferentes medios. Desviación estándar
La desviación estándar es una medida de variabilidad. Define el ancho de la distribución normal. La desviación estándar determina qué tan lejos de la media tiende a caer los valores. Representa la distancia típica entre las observaciones y el promedio.
En un gráfico, cambiar la desviación estándar se tensa o extiende el ancho de la distribución a lo largo del eje X. Las desviaciones estándar más grandes producen distribuciones que se extienden más.
Gráfico que muestra distribuciones normales con diferentes desviaciones estándar.
Cuando tiene distribuciones estrechas, las probabilidades son más altas de que los valores no se alejarán de la media. A medida que aumenta la propagación de la distribución, la probabilidad de que las observaciones estén más lejos de la media también aumenta. Parámetros de población versus estimaciones de muestra
La media y la desviación estándar son valores de parámetros que se aplican a poblaciones completas. Para la distribución normal, los estadísticos significan los parámetros utilizando el símbolo griego μ (MU) para la media de la población y σ (Sigma) para la desviación estándar de la población.
Desafortunadamente, los parámetros de población generalmente son desconocidos porque generalmente es imposible medir una población completa. Sin embargo, puede usar muestras aleatorias para calcular estimaciones de estos parámetros. Los estadísticos representan estimaciones de muestra de estos parámetros utilizando X̅ para la media de muestra y S para la desviación estándar de la muestra.
Publicaciones relacionadas: Medidas de tendencia central y medidas de variabilidad Propiedades comunes para todas las formas de la distribución normal
A pesar de las diferentes formas, todas las formas de la distribución normal tienen las siguientes propiedades características.
They’re all symmetric. The normal distribution cannot model skewed distributions.
The mean, median, and mode are all equal.
Half of the population is less than the mean and half is greater than the mean.
The Empirical Rule allows you to determine the proportion of values that fall within certain distances from the mean. More on this below!
Si bien la distribución normal es esencial en las estadísticas, es solo una de las muchas distribuciones de probabilidad, y no se ajusta a todas las poblaciones. Para aprender cómo determinar si la distribución normal proporciona el mejor ajuste a sus datos de muestra, lea mis publicaciones sobre cómo identificar la distribución de sus datos y evaluar la normalidad: histogramas versus gráficos de probabilidad normales. La regla empírica para la distribución normal
Cuando tiene datos normalmente distribuidos, la desviación estándar se vuelve particularmente valiosa. Puede usarlo para determinar la proporción de los valores que caen dentro de un número específico de desviaciones estándar de la media. Por ejemplo, en una distribución normal, el 68% de las observaciones caen dentro de la desviación estándar +/- 1 de la media. Esta propiedad es parte de la regla empírica, que describe el porcentaje de datos que se encuentran dentro de números específicos de desviaciones estándar de la media para las curvas en forma de campana. Media +/- Desviaciones estándar Porcentaje de datos contenía 1 68% 2 95% 3 99.7%
Veamos un ejemplo de entrega de pizza. Suponga que un restaurante de pizza tiene un tiempo de entrega medio de 30 minutos y una desviación estándar de 5 minutos. Usando la regla empírica, podemos determinar que el 68% de los tiempos de entrega están entre 25 y 35 minutos (30 +/- 5), el 95% están entre 20-40 minutos (30 +/- 2 5) y el 99.7% están entre 15-45 minutos (30 +/- 3 5). El cuadro a continuación ilustra esta propiedad gráficamente.
Gráfico que muestra una distribución normal con áreas divididas por desviaciones estándar. Distribución normal estándar y puntajes estándar
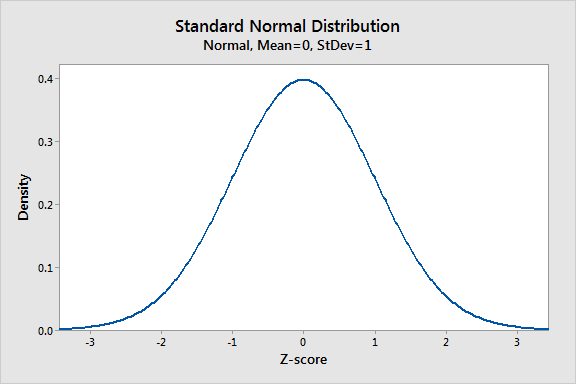
Como hemos visto anteriormente, la distribución normal tiene muchas formas diferentes según los valores de los parámetros. Sin embargo, la distribución normal estándar es un caso especial de la distribución normal donde la media es cero y la desviación estándar es 1. Esta distribución también se conoce como distribución Z.
Un valor en la distribución normal estándar se conoce como puntaje estándar o una puntuación Z. Una puntuación estándar representa el número de desviaciones estándar por encima o por debajo de la media que cae una observación específica. Por ejemplo, una puntuación estándar de 1.5 indica que la observación es 1.5 desviaciones estándar por encima de la media. Por otro lado, una puntuación negativa representa un valor por debajo del promedio. La media tiene una puntuación Z de 0.
Gráfico que muestre una distribución normal estándar.
Supongamos que pesa una manzana y pesa 110 gramos. No hay forma de saber solo por el peso cómo se compara esta manzana con otras manzanas. Sin embargo, como verá, después de calcular su puntaje Z, sabes dónde cae en relación con otras manzanas. Estandarización: cómo calcular las puntuaciones Z
Los puntajes estándar son una excelente manera de comprender dónde cae una observación específica en relación con toda la distribución. También le permiten tomar observaciones extraídas de poblaciones normalmente distribuidas que tienen diferentes medios y desviaciones estándar y colocarlas en una escala estándar. Esta escala estándar le permite comparar observaciones que de otro modo serían difíciles.
Este proceso se llama estandarización y le permite comparar observaciones y calcular las probabilidades en diferentes poblaciones. En otras palabras, le permite comparar manzanas con naranjas. ¿No son las estadísticas geniales!
Para estandarizar sus datos, debe convertir las mediciones sin procesar en puntajes Z.
Para calcular la puntuación estándar para una observación, tome la medición sin procesar, reste la media y divida por la desviación estándar. Matemáticamente, la fórmula para ese proceso es la siguiente:
Z = { displaystyle frac { text {x} - mu} { sigma}}
X representa el valor en bruto de la medición de interés. Mu y Sigma representan los parámetros para la población de los cuales se extrajo la observación.
Después de estandarizar sus datos, puede colocarlos dentro de la distribución normal estándar. De esta manera, la estandarización le permite comparar diferentes tipos de observaciones en función de donde cada observación cae dentro de su propia distribución. Ejemplo del uso de puntajes estándar para hacer una comparación de manzanas a naranjas
Supongamos que literalmente queremos comparar manzanas con naranjas. Específicamente, comparemos sus pesos. Imagine que tenemos una manzana que pesa 110 gramos y una naranja que pesa 100 gramos.
Si comparamos los valores en bruto, es fácil ver que la manzana pesa más que la naranja. Sin embargo, comparemos sus puntajes estándar. Para hacer esto, necesitaremos conocer las propiedades de las distribuciones de peso para manzanas y naranjas. Suponga que los pesos de las manzanas y las naranjas siguen una distribución normal con los siguientes valores de parámetros: las naranjas de manzanas significan Gramos de peso 100 140 desviación estándar 15 25
Ahora calcularemos las puntuaciones Z:
Apple = 110-100/15 = 0.667
Orange = 100-140/25 = -1.6
La puntuación Z para la Apple (0.667) es positiva, lo que significa que nuestra manzana pesa más que la manzana promedio. No es un valor extremo de ninguna manera, pero está por encima del promedio de manzanas. Por otro lado, la naranja tiene un puntaje Z bastante negativo (-1.6). Está bastante por debajo del peso medio para las naranjas. He colocado estos valores Z en la distribución normal estándar a continuación.
Gráfico de una distribución normal estándar que compara las manzanas con las naranjas utilizando un puntaje Z.
Si bien nuestra manzana pesa más que nuestra naranja, estamos comparando una manzana algo más pesada que el promedio con una naranja francamente insignificante. Usando puntajes Z, hemos aprendido cómo cada fruta se ajusta dentro de su propia distribución y cómo se comparan entre sí. Encontrar áreas bajo la curva de una distribución normal
La distribución normal es una distribución de probabilidad. Al igual que con cualquier distribución de probabilidad, la proporción del área que cae bajo la curva entre dos puntos en un gráfico de distribución de probabilidad indica la probabilidad de que un valor caiga dentro de ese intervalo. Para obtener más información sobre esta propiedad, lea mi publicación sobre la comprensión de las distribuciones de probabilidad.
Por lo general, uso software estadístico para encontrar áreas bajo la curva. Sin embargo, cuando trabaja con la distribución normal y convierte los valores en puntajes estándar, puede calcular las áreas buscando puntajes Z en una tabla de distribución normal estándar.
Debido a que hay un número infinito de diferentes distribuciones normales, los editores no pueden imprimir una tabla para cada distribución. Sin embargo, puede transformar los valores de cualquier distribución normal en puntajes Z, y luego usar una tabla de puntajes estándar para calcular las probabilidades. Usando una tabla de puntajes Z
Tomemos el puntaje Z para nuestra manzana (0.667) y la usemos para determinar su percentil de peso. Un percentil es la proporción de una población que cae por debajo de un valor específico. En consecuencia, para determinar el percentil, necesitamos encontrar el área que corresponde al rango de puntajes Z que son inferiores a 0.667. En la parte de la tabla a continuación, la puntuación Z más cercana a la nuestra es 0.65, que usaremos.
La fotografía muestra una parte de una tabla de puntajes estándar (puntajes Z).
El truco con estas tablas es usar los valores junto con las propiedades de la distribución normal para calcular la probabilidad que necesita. El valor de la tabla indica que el área de la curva entre -0.65 y +0.65 es del 48.43%. Sin embargo, eso no es lo que queremos saber. Queremos el área que es inferior a una puntuación Z de 0.65.
Sabemos que las dos mitades de la distribución normal son imágenes de espejo entre sí. Entonces, si el área para el intervalo de -0.65 y +0.65 es 48.43%, entonces el rango de 0 a +0.65 debe ser la mitad de eso: 48.43/2 = 24.215%. Además, sabemos que el área para todos los puntajes inferiores a cero es la mitad (50%) de la distribución.
Por lo tanto, el área para todos los puntajes de hasta 0.65 = 50% + 24.215% = 74.215%
Nuestra manzana es aproximadamente el percentil 74.
A continuación se muestra un gráfico de distribución de probabilidad producido por un software estadístico que muestra el mismo percentil junto con una representación gráfica del área correspondiente bajo la curva. El valor es ligeramente diferente porque utilizamos un puntaje Z de 0.65 de la tabla, mientras que el software usa el valor más preciso de 0.667.
Un gráfico de distribución de probabilidad que muestra gráficamente un percentil usando un puntaje Z. Otras razones por las cuales la distribución normal es importante
Además de todo lo anterior, hay varias otras razones por las cuales la distribución normal es crucial en las estadísticas.
Some statistical hypothesis tests assume that the data follow a normal distribution. However, as I explain in my post about parametric and nonparametric tests, there’s more to it than only whether the data are normally distributed.
Linear and nonlinear regression both assume that the residuals follow a normal distribution. Learn more in my post about assessing residual plots.
The central limit theorem states that as the sample size increases, the sampling distribution of the mean follows a normal distribution even when the underlying distribution of the original variable is non-normal.
¡Eso fue bastante sobre la distribución normal! Con suerte, puede entender que es crucial debido a las muchas formas en que los analistas lo usan.
Fuente: https://statisticsbyjim.com/basics/normal-distribution/

Probabilidad acumulativa de una distribución normal con el valor esperado 0 y la desviación estándar 1: 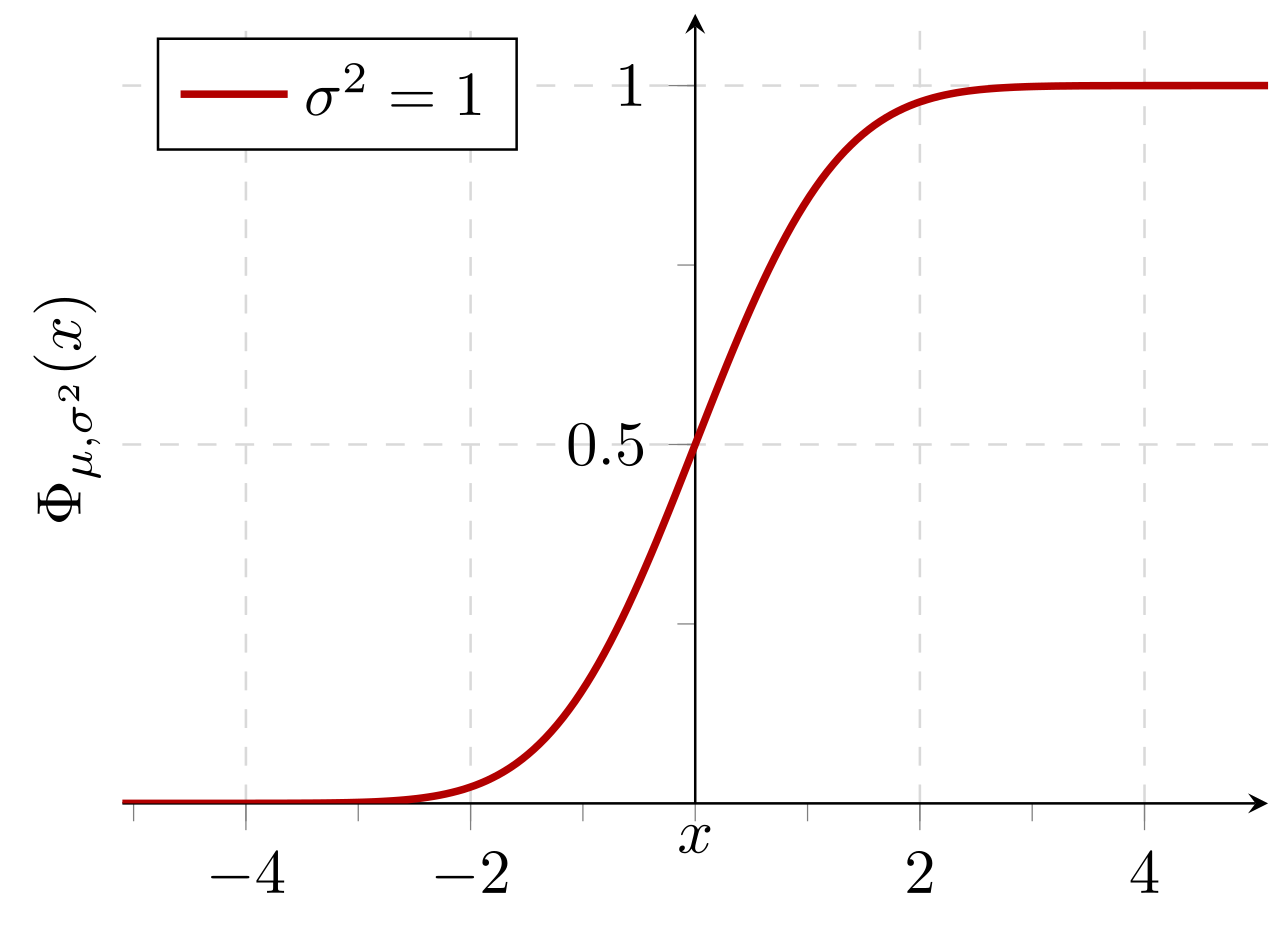
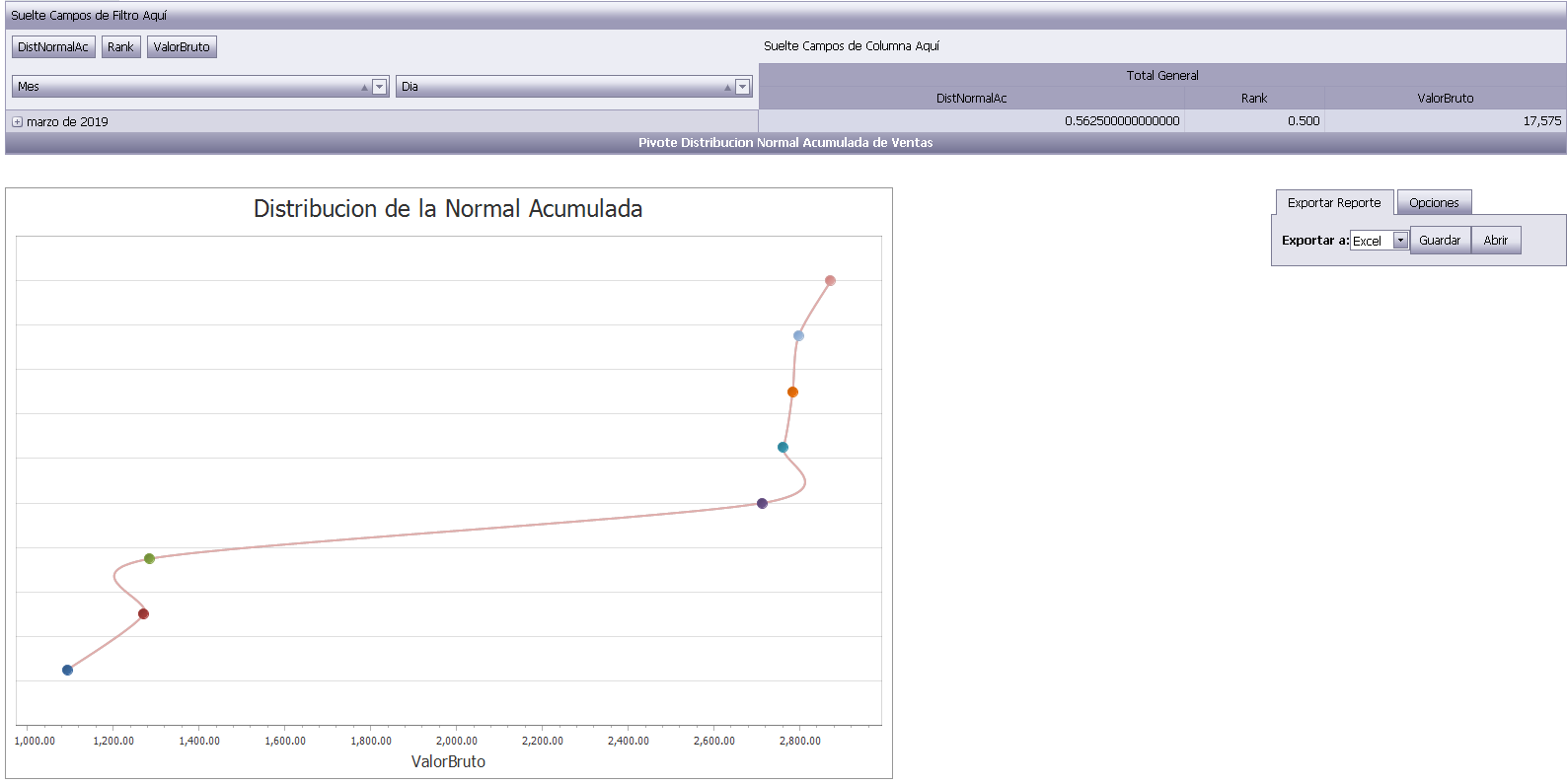
Este es un software gratuito y sin gabidos lanzado en el dominio público; consulte el archivo de licencia para obtener más detalles.
Hecho con ❤️ por Javier Cañon.