SQL Server Normalverteilung, Gauß oder Glockenkurve
Die Normalverteilung ist die wichtigste Wahrscheinlichkeitsverteilung in Statistiken, da sie zu vielen natürlichen Phänomenen passt. Zum Beispiel folgen Höhen, Blutdruck, Messfehler und IQ -Werte der Normalverteilung. Es ist auch als Gaußsche Verteilung und die Glockenkurve bekannt.
Die Normalverteilung ist eine Wahrscheinlichkeitsfunktion, die beschreibt, wie die Werte einer Variablen verteilt sind. Es handelt sich um eine symmetrische Verteilung, bei der sich die meisten Beobachtungen um den zentralen Peak und die Wahrscheinlichkeiten für Werte weiter vom mittleren Verjüngung in beiden Richtungen entfernt. Extremwerte in beiden Schwänzen der Verteilung sind ähnlich unwahrscheinlich.
In diesem Blog-Beitrag erfahren Sie, wie Sie die Normalverteilung, ihre Parameter und die Berechnung von Z-Scores verwenden, um Ihre Daten zu standardisieren und Wahrscheinlichkeiten zu finden. Beispiel für normal verteilte Daten: Höhen
Höhendaten werden normal verteilt. Die Verteilung in diesem Beispiel passt zu echten Daten, die ich während einer Studie von 14-jährigen Mädchen gesammelt habe.
Normalverteilung der Höhen.
Wie Sie sehen können, folgt die Verteilung der Höhen dem typischen Muster für alle Normalverteilungen. Die meisten Mädchen sind nahe am Durchschnitt (1,512 Meter). Kleine Unterschiede zwischen der Höhe eines Individuums und dem Mittelwert treten häufiger auf als wesentliche Abweichungen vom Mittelwert. Die Standardabweichung beträgt 0,0741 m, was den typischen Abstand anzeigt, dass einzelne Mädchen dazu neigen, von der mittleren Höhe zu fallen.
Die Verteilung ist symmetrisch. Die Anzahl der Mädchen, die kürzer als der Durchschnitt kürzer sind, entspricht der Anzahl der Mädchen, die mehr als durchschnittlich sind. In beiden Schwänzen der Verteilung treten extrem kurze Mädchen so selten wie extrem große Mädchen auf. Parameter der Normalverteilung
Wie bei jeder Wahrscheinlichkeitsverteilung definieren die Parameter für die Normalverteilung ihre Form und Wahrscheinlichkeiten vollständig. Die Normalverteilung hat zwei Parameter, den Mittelwert und die Standardabweichung. Die Normalverteilung hat nicht nur eine Form. Stattdessen ändert sich die Form basierend auf den Parameterwerten, wie in den folgenden Grafiken gezeigt. Bedeuten
Der Mittelwert ist die zentrale Tendenz der Verteilung. Es definiert den Ort des Peaks für Normalverteilungen. Die meisten Werte gruppieren sich um den Mittelwert. Durch das Ändern des Mittelwerts verschiebt in einem Diagramm die gesamte Kurve nach links oder rechts auf der X-Achse.
Grafik, die Normalverteilungen mit unterschiedlichen Mitteln anzeigen. Standardabweichung
Die Standardabweichung ist ein Maß für die Variabilität. Es definiert die Breite der Normalverteilung. Die Standardabweichung bestimmt, wie weit der Mittelwert von den Werten entfernt ist, um zu fallen. Es repräsentiert den typischen Abstand zwischen den Beobachtungen und dem Durchschnitt.
Wenn Sie in einem Diagramm die Standardabweichung ändern, wird die Breite der Verteilung entlang der X-Achse festgezogen oder ausbreitet. Größere Standardabweichungen erzeugen Verteilungen, die mehr verteilt sind.
Graph, das Normalverteilungen mit unterschiedlichen Standardabweichungen anzeigt.
Wenn Sie enge Verteilungen haben, sind die Wahrscheinlichkeiten höher, als die Werte nicht weit vom Mittelwert abfallen. Wenn Sie die Ausbreitung der Verteilung erhöhen, nimmt die Wahrscheinlichkeit, dass die Beobachtungen weiter vom Mittelwert entfernt sein werden. Populationsparameter gegenüber Stichprobenschätzungen
Der Mittelwert und die Standardabweichung sind Parameterwerte, die für ganze Populationen gelten. Für die Normalverteilung bedeuten Statistiker die Parameter, indem sie das griechische Symbol μ (MU) für den Bevölkerungsmittelwert und σ (Sigma) für die Bevölkerungsstandardabweichung verwenden.
Leider sind die Bevölkerungsparameter normalerweise nicht bekannt, da es im Allgemeinen unmöglich ist, eine ganze Bevölkerung zu messen. Sie können jedoch zufällige Stichproben verwenden, um die Schätzungen dieser Parameter zu berechnen. Statistiker repräsentieren Stichprobenschätzungen dieser Parameter unter Verwendung von X̅ für den Stichprobenmittelwert und S für die Stichprobenstandardabweichung.
Verwandte Stellen: Maßnahmen zur zentralen Tendenz und der Messungen der Variabilität gemeinsame Eigenschaften für alle Formen der Normalverteilung
Trotz der verschiedenen Formen haben alle Formen der Normalverteilung die folgenden charakteristischen Eigenschaften.
They’re all symmetric. The normal distribution cannot model skewed distributions.
The mean, median, and mode are all equal.
Half of the population is less than the mean and half is greater than the mean.
The Empirical Rule allows you to determine the proportion of values that fall within certain distances from the mean. More on this below!
Während die Normalverteilung in Statistiken wesentlich ist, ist sie nur eine von vielen Wahrscheinlichkeitsverteilungen und passt nicht zu allen Populationen. Um zu erfahren, wie Sie feststellen, ob die Normalverteilung die besten Anpassungen Ihrer Beispieldaten bietet, lesen Sie meine Beiträge zur Identifizierung der Verteilung Ihrer Daten und zur Bewertung der Normalität: Histogramme im Vergleich zu normalen Wahrscheinlichkeitsnarks. Die empirische Regel für die Normalverteilung
Wenn Sie normalerweise verteilte Daten haben, wird die Standardabweichung besonders wertvoll. Sie können es verwenden, um den Anteil der Werte zu bestimmen, die innerhalb einer bestimmten Anzahl von Standardabweichungen vom Mittelwert fallen. Beispielsweise fallen 68% der Beobachtungen in einer Normalverteilung innerhalb der Standardabweichung von +/- 1 vom Mittelwert. Diese Eigenschaft ist Teil der empirischen Regel, die den Prozentsatz der Daten beschreibt, die in bestimmte Anzahl von Standardabweichungen vom Mittelwert für glockenförmige Kurven fallen. Mittelwert +/- Standardabweichungen Prozentsatz der Daten enthielten 1 68% 2 95% 3 99,7%
Schauen wir uns ein Beispiel für Pizza -Lieferung an. Angenommen, ein Pizza -Restaurant hat eine mittlere Lieferzeit von 30 Minuten und eine Standardabweichung von 5 Minuten. Mit der empirischen Regel können wir feststellen, dass 68% der Lieferzeiten zwischen 25-35 Minuten (30 +/- 5), 95% zwischen 20-40 Minuten (30 +/- 2 5) liegen und 99,7% zwischen 15-45 Minuten (30 +/- 3 5) liegen . Das folgende Diagramm zeigt diese Eigenschaft grafisch.
Graph, das eine Normalverteilung mit Bereichen angezeigt wird, geteilt durch Standardabweichungen. Standard -Normalverteilung und Standardwerte
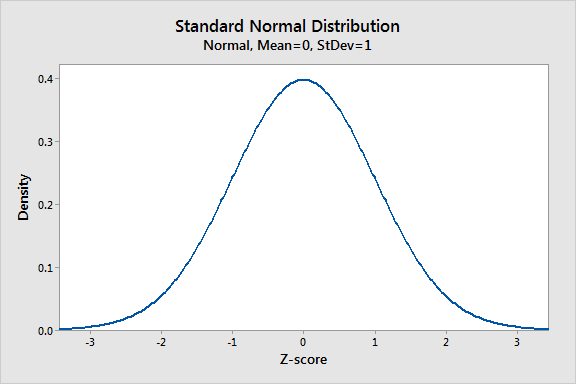
Wie wir oben gesehen haben, hat die Normalverteilung abhängig von den Parameterwerten viele verschiedene Formen. Die Standard-Normalverteilung ist jedoch ein spezieller Fall der Normalverteilung, bei dem der Mittelwert Null ist und die Standardabweichung 1 ist. Diese Verteilung wird auch als Z-Verteilung bezeichnet.
Ein Wert für die Standardnormalverteilung wird als Standardbewertung oder Z-Score bezeichnet. Eine Standardbewertung stellt die Anzahl der Standardabweichungen über oder unter dem Mittelwert dar, dass eine bestimmte Beobachtung fällt. Beispielsweise zeigt ein Standardwert von 1,5 an, dass die Beobachtung 1,5 Standardabweichungen über dem Mittelwert liegt. Andererseits stellt eine negative Punktzahl einen Wert unter dem Durchschnitt dar. Der Mittelwert hat einen Z-Score von 0.
Grafik, die eine Standardnormalverteilung anzeigen.
Angenommen, Sie wiegen einen Apfel und er wiegt 110 Gramm. Es gibt keine Möglichkeit, allein aus dem Gewicht zu erkennen, wie dieser Apfel mit anderen Äpfeln verglichen wird. Wie Sie jedoch sehen werden, wissen Sie, nachdem Sie den Z-Score berechnet haben, wo es im Verhältnis zu anderen Äpfeln fällt. Standardisierung: Berechnung von Z-Scores
Standardwerte sind eine großartige Möglichkeit zu verstehen, wo eine bestimmte Beobachtung im Verhältnis zur gesamten Verteilung fällt. Sie ermöglichen es Ihnen auch, Beobachtungen aus normalverteilten Populationen mit unterschiedlichen Mitteln und Standardabweichungen zu übernehmen und auf eine Standardmaßstab zu platzieren. Mit dieser Standardskala können Sie Beobachtungen vergleichen, die sonst schwierig wären.
Dieser Prozess wird als Standardisierung bezeichnet und ermöglicht es Ihnen, Beobachtungen zu vergleichen und die Wahrscheinlichkeiten über verschiedene Populationen hinweg zu berechnen. Mit anderen Worten, es ermöglicht es Ihnen, Äpfel mit Orangen zu vergleichen. Ist Statistiken nicht großartig!
Um Ihre Daten zu standardisieren, müssen Sie die RAW-Messungen in Z-Scores umwandeln.
Um den Standardwert für eine Beobachtung zu berechnen, nehmen Sie die RAW -Messung an, subtrahieren Sie den Mittelwert und teilen Sie dies durch die Standardabweichung. Mathematisch ist die Formel für diesen Prozess die folgende:
Z = { displaystyle frac { text {x} - mu} { sigma}}
X repräsentiert den Rohwert der Messung von Interesse. MU und Sigma repräsentieren die Parameter für die Bevölkerung, aus der die Beobachtung stammte.
Nachdem Sie Ihre Daten standardisieren, können Sie sie in die Standardnormalverteilung einfügen. Auf diese Weise können Sie auf diese Weise verschiedene Arten von Beobachtungen vergleichen, basierend darauf, wo jede Beobachtung in ihre eigene Verteilung fällt. Beispiel für die Verwendung von Standardwerten, um Äpfel für Orangenvergleiche zu erstellen
Angenommen, wir wollen buchstäblich Äpfel mit Orangen vergleichen. Vergleichen wir im Einzelnen ihre Gewichte. Stellen Sie sich vor, wir haben einen Apfel, der 110 Gramm wiegt und eine Orange mit einem Gewicht von 100 Gramm.
Wenn wir die Rohwerte vergleichen, ist es leicht zu erkennen, dass der Apfel mehr wiegt als die Orange. Vergleichen wir jedoch ihre Standardwerte. Dazu müssen wir die Eigenschaften der Gewichtsverteilungen für Äpfel und Orangen kennen. Angenommen, die Gewichte von Äpfeln und Orangen folgen einer Normalverteilung mit den folgenden Parameterwerten
Jetzt werden wir die Z-Scores berechnen:
Apple = 110-100/15 = 0.667
Orange = 100-140/25 = -1.6
Der Z-Score für den Apfel (0,667) ist positiv, was bedeutet, dass unser Apfel mehr wiegt als der durchschnittliche Apfel. Es ist keineswegs ein extremer Wert, aber für Äpfel ist es überdurchschnittlich. Andererseits hat die Orange ziemlich negative Z-Score (-1,6). Es liegt ziemlich weit unter dem mittleren Gewicht für Orangen. Ich habe diese Z-Werte in die Standardnormalverteilung unten gestellt.
Grafik einer Standardnormalverteilung, die Äpfel mit Orangen mit einem Z-Score vergleicht.
Während unser Apfel mehr wies unser Orange wiegen, vergleichen wir einen etwas schwereren als durchschnittlichen Apfel mit einer geradezu mickrigen Orange! Mit Z-Scores haben wir gelernt, wie jede Frucht in ihre eigene Verteilung passt und wie sie sich miteinander vergleichen. Auffinden von Bereichen unter der Kurve einer Normalverteilung
Die Normalverteilung ist eine Wahrscheinlichkeitsverteilung. Wie bei jeder Wahrscheinlichkeitsverteilung zeigt der Anteil des Bereichs, der zwischen zwei Punkten auf einem Wahrscheinlichkeitsverteilungsdiagramm unter die Kurve fällt, die Wahrscheinlichkeit, dass ein Wert innerhalb dieses Intervalls fällt. Um mehr über diese Eigenschaft zu erfahren, lesen Sie meinen Beitrag über das Verständnis der Wahrscheinlichkeitsverteilungen.
Normalerweise verwende ich statistische Software, um Bereiche unter der Kurve zu finden. Wenn Sie jedoch mit der Normalverteilung arbeiten und Werte in Standard-Scores konvertieren, können Sie Bereiche berechnen, indem Sie Z-Scores in einer Standardnormalverteilungstabelle nachschlagen.
Da es eine unendliche Anzahl verschiedener Normalverteilungen gibt, können Verlage für jede Verteilung keine Tabelle drucken. Sie können die Werte jedoch von jeder Normalverteilung in Z-Scores umwandeln und dann eine Tabelle mit Standard-Scores verwenden, um die Wahrscheinlichkeiten zu berechnen. Verwenden einer Tabelle von Z-Scores
Nehmen wir den Z-Score für unseren Apfel (0,667) und verwenden Sie ihn, um das Gewichts Prozentsatz zu bestimmen. Ein Perzentil ist der Anteil einer Bevölkerung, der unter einen bestimmten Wert fällt. Um das Perzentil zu bestimmen, müssen wir folglich die Fläche ermitteln, die dem Bereich der Z-Scores entspricht, die weniger als 0,667 sind. Im Abschnitt der folgenden Tabelle beträgt der nächstgelegene Z-Score für uns 0,65, was wir verwenden werden.
Das Foto zeigt einen Teil einer Tabelle mit Standardwerten (Z-Scores).
Der Trick mit diesen Tabellen besteht darin, die Werte in Verbindung mit den Eigenschaften der Normalverteilung zu verwenden, um die Wahrscheinlichkeit zu berechnen, die Sie benötigen. Der Tabellenwert zeigt an, dass die Fläche der Kurve zwischen -0,65 und +0,65 48,43%beträgt. Das wollen wir jedoch nicht wissen. Wir wollen den Bereich, der weniger als einen Z-Score von 0,65 ist.
Wir wissen, dass die beiden Hälften der Normalverteilung Spiegelbilder voneinander sind. Wenn der Bereich für das Intervall von -0,65 und +0,65 48,43%beträgt, muss der Bereich von 0 bis +0,65 die Hälfte davon sein: 48,43/2 = 24,215%. Darüber hinaus wissen wir, dass der Bereich für alle Punkte von weniger als Null die Hälfte (50%) der Verteilung beträgt.
Daher die Fläche für alle Punktzahlen von bis zu 0,65 = 50% + 24,215% = 74,215%
Unser Apfel befindet sich ungefähr im 74. Perzentil.
Im Folgenden finden Sie ein Wahrscheinlichkeitsverteilungsdiagramm, das von statistischer Software erzeugt wird und das gleiche Perzentil zusammen mit einer grafischen Darstellung des entsprechenden Bereichs unter der Kurve zeigt. Der Wert ist geringfügig unterschiedlich, da wir einen Z-Score von 0,65 aus der Tabelle verwendet haben, während die Software den genaueren Wert von 0,667 verwendet.
Ein Wahrscheinlichkeitsverteilungsdiagramm, das ein Perzentil mit einem Z-Score grafisch zeigt. Andere Gründe, warum die Normalverteilung wichtig ist
Zusätzlich zu all dem oben genannten gibt es mehrere andere Gründe, warum die Normalverteilung in der Statistik von entscheidender Bedeutung ist.
Some statistical hypothesis tests assume that the data follow a normal distribution. However, as I explain in my post about parametric and nonparametric tests, there’s more to it than only whether the data are normally distributed.
Linear and nonlinear regression both assume that the residuals follow a normal distribution. Learn more in my post about assessing residual plots.
The central limit theorem states that as the sample size increases, the sampling distribution of the mean follows a normal distribution even when the underlying distribution of the original variable is non-normal.
Das war einiges an der Normalverteilung! Hoffentlich können Sie verstehen, dass es aufgrund der vielen Möglichkeiten, die Analysten verwenden, von entscheidender Bedeutung ist.
Quelle: https://statisticsbyjim.com/basics/normal-distribution/

Kumulative Wahrscheinlichkeit einer Normalverteilung mit dem erwarteten Wert 0 und der Standardabweichung 1: 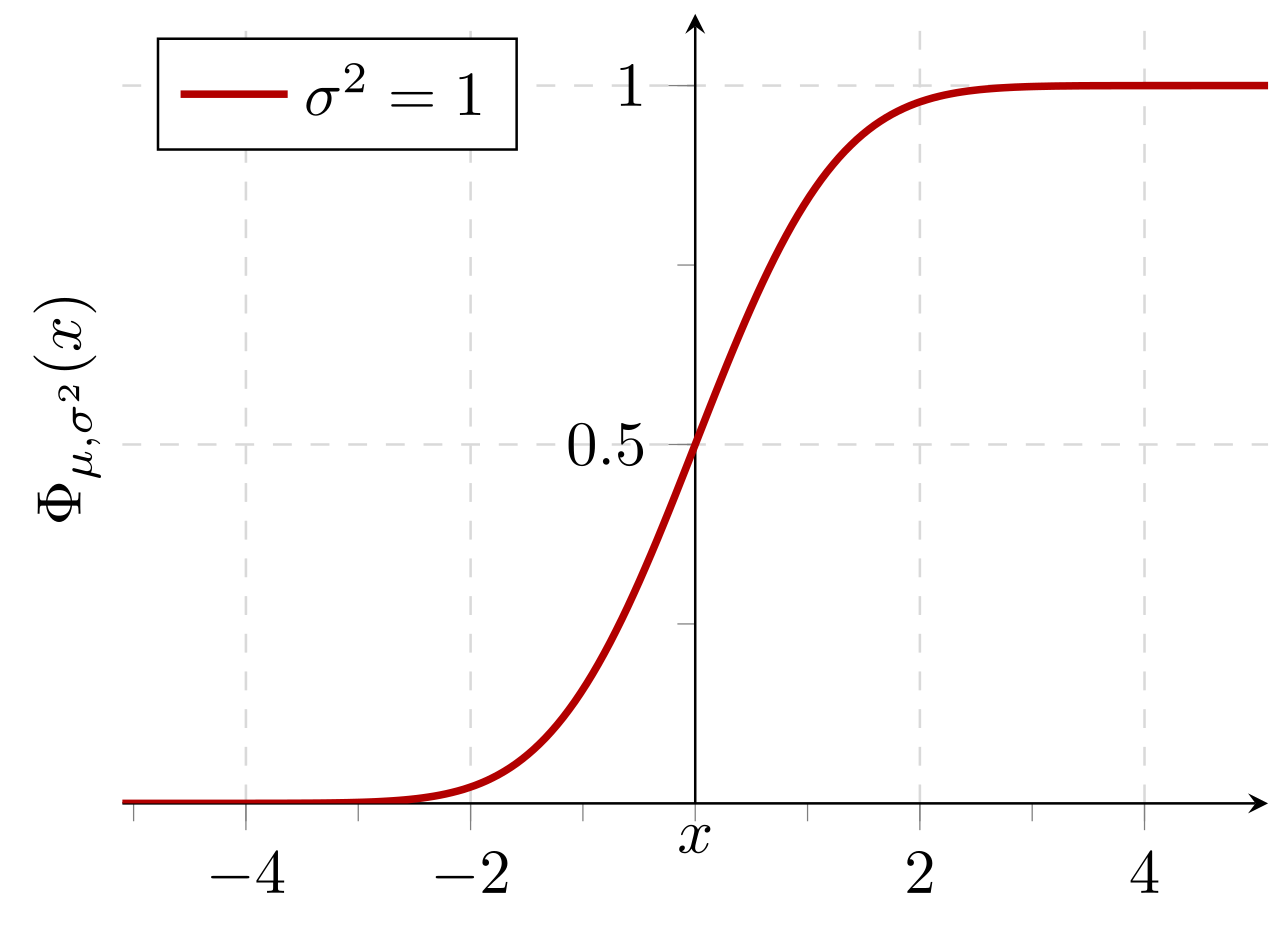
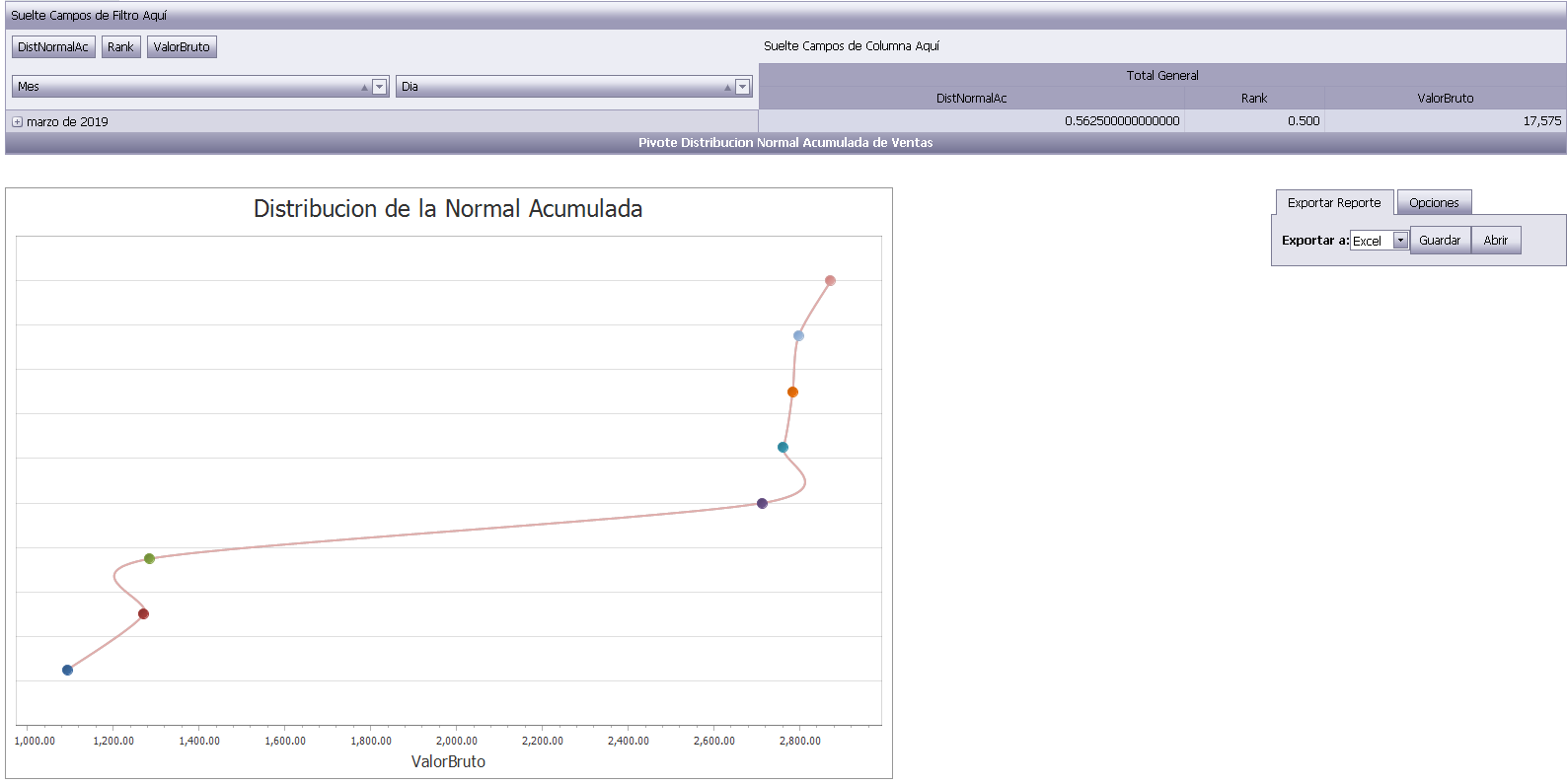
Dies ist kostenlose und nicht belastete Software, die öffentlich zugänglich gemacht wird. Weitere Informationen finden Sie in der Lizenzdatei.
Hergestellt mit ❤️ von Javier Cañon.