SQL Server Distribusi Normal, Gauss atau Bell Curve
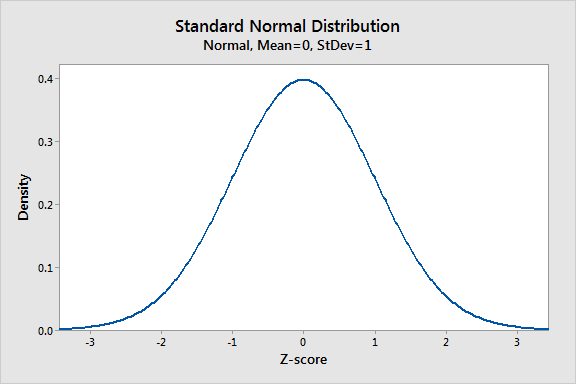
Distribusi normal adalah distribusi probabilitas yang paling penting dalam statistik karena cocok dengan banyak fenomena alam. Misalnya, ketinggian, tekanan darah, kesalahan pengukuran, dan skor IQ mengikuti distribusi normal. Ini juga dikenal sebagai distribusi Gaussian dan kurva lonceng.
Distribusi normal adalah fungsi probabilitas yang menjelaskan bagaimana nilai variabel didistribusikan. Ini adalah distribusi simetris di mana sebagian besar pengamatan mengelompok di sekitar puncak pusat dan probabilitas untuk nilai -nilai lebih jauh dari lancip rata -rata yang sama di kedua arah. Nilai ekstrem di kedua ekor distribusi sama tidak mungkin.
Dalam posting blog ini, Anda akan belajar cara menggunakan distribusi normal, parameternya, dan cara menghitung skor-z untuk menstandarkan data Anda dan menemukan probabilitas. Contoh data yang didistribusikan secara normal: ketinggian
Data tinggi didistribusikan secara normal. Distribusi dalam contoh ini cocok dengan data nyata yang saya kumpulkan dari anak perempuan berusia 14 tahun selama penelitian.
Distribusi ketinggian normal.
Seperti yang Anda lihat, distribusi ketinggian mengikuti pola khas untuk semua distribusi normal. Sebagian besar gadis dekat dengan rata -rata (1,512 meter). Perbedaan kecil antara tinggi individu dan rata -rata terjadi lebih sering daripada penyimpangan substansial dari rata -rata. Deviasi standar adalah 0,0741m, yang menunjukkan jarak khas yang cenderung jatuh dari tinggi rata -rata.
Distribusinya simetris. Jumlah gadis yang lebih pendek dari rata -rata sama dengan jumlah gadis yang lebih tinggi dari rata -rata. Di kedua ekor distribusi, gadis -gadis yang sangat pendek terjadi jarang seperti gadis yang sangat tinggi. Parameter distribusi normal
Seperti halnya distribusi probabilitas apa pun, parameter untuk distribusi normal menentukan bentuk dan probabilitasnya sepenuhnya. Distribusi normal memiliki dua parameter, rata -rata dan standar deviasi. Distribusi normal tidak hanya memiliki satu bentuk. Sebaliknya, bentuk berubah berdasarkan nilai parameter, seperti yang ditunjukkan pada grafik di bawah ini. Berarti
Rata -rata adalah kecenderungan utama distribusi. Ini mendefinisikan lokasi puncak untuk distribusi normal. Sebagian besar nilai mengelompok di sekitar rata -rata. Pada grafik, mengubah rata-rata menggeser seluruh kurva ke kiri atau kanan pada sumbu x.
Grafik yang menampilkan distribusi normal dengan cara yang berbeda. Deviasi standar
Deviasi standar adalah ukuran variabilitas. Ini mendefinisikan lebar distribusi normal. Deviasi standar menentukan seberapa jauh dari rata -rata nilai cenderung turun. Ini mewakili jarak khas antara pengamatan dan rata -rata.
Pada grafik, mengubah standar deviasi baik mengencangkan atau menyebarkan lebar distribusi sepanjang sumbu x. Penyimpangan standar yang lebih besar menghasilkan distribusi yang lebih tersebar.
Grafik yang menampilkan distribusi normal dengan standar deviasi yang berbeda.
Ketika Anda memiliki distribusi sempit, probabilitas lebih tinggi karena nilai tidak akan jauh dari rata -rata. Ketika Anda meningkatkan penyebaran distribusi, kemungkinan bahwa pengamatan akan jauh dari rata -rata juga meningkat. Parameter populasi versus estimasi sampel
Rata -rata dan standar deviasi adalah nilai parameter yang berlaku untuk seluruh populasi. Untuk distribusi normal, ahli statistik menandakan parameter dengan menggunakan simbol Yunani μ (MU) untuk rata -rata populasi dan σ (Sigma) untuk standar deviasi populasi.
Sayangnya, parameter populasi biasanya tidak diketahui karena umumnya tidak mungkin mengukur seluruh populasi. Namun, Anda dapat menggunakan sampel acak untuk menghitung estimasi parameter ini. Statistik mewakili estimasi sampel parameter ini menggunakan X̅ untuk rata -rata sampel dan S untuk standar deviasi sampel.
Posting Terkait: Ukuran Kecenderungan Pusat dan Ukuran Variabilitas Properti Umum Untuk Semua Bentuk Distribusi Normal
Terlepas dari bentuk yang berbeda, semua bentuk distribusi normal memiliki sifat karakteristik berikut.
They’re all symmetric. The normal distribution cannot model skewed distributions.
The mean, median, and mode are all equal.
Half of the population is less than the mean and half is greater than the mean.
The Empirical Rule allows you to determine the proportion of values that fall within certain distances from the mean. More on this below!
Sementara distribusi normal sangat penting dalam statistik, itu hanyalah salah satu dari banyak distribusi probabilitas, dan tidak sesuai dengan semua populasi. Untuk mempelajari cara menentukan apakah distribusi normal memberikan yang paling cocok untuk data sampel Anda, baca posting saya tentang cara mengidentifikasi distribusi data Anda dan menilai normalitas: histogram vs plot probabilitas normal. Aturan empiris untuk distribusi normal
Ketika Anda memiliki data yang didistribusikan secara normal, standar deviasi menjadi sangat berharga. Anda dapat menggunakannya untuk menentukan proporsi nilai -nilai yang termasuk dalam jumlah standar deviasi yang ditentukan dari rata -rata. Misalnya, dalam distribusi normal, 68% dari pengamatan termasuk dalam +/- 1 standar deviasi dari rata-rata. Properti ini adalah bagian dari aturan empiris, yang menggambarkan persentase data yang termasuk dalam jumlah spesifik standar deviasi dari rata-rata untuk kurva berbentuk lonceng. Rata-rata +/- standar deviasi data berisi 1 68% 2 95% 3 99,7%
Mari kita lihat contoh pengiriman pizza. Asumsikan bahwa restoran pizza memiliki waktu pengiriman rata -rata 30 menit dan standar deviasi 5 menit. Dengan menggunakan aturan empiris, kita dapat menentukan bahwa 68% dari waktu pengiriman adalah antara 25-35 menit (30 +/- 5), 95% adalah antara 20-40 menit (30 +/- 2 5), dan 99,7% antara 15-45 menit (30 +/- 3 5). Bagan di bawah ini menggambarkan properti ini secara grafis.
Grafik yang menampilkan distribusi normal dengan area dibagi dengan standar deviasi. Distribusi normal standar dan skor standar
Seperti yang telah kita lihat di atas, distribusi normal memiliki banyak bentuk yang berbeda tergantung pada nilai parameter. Namun, distribusi normal standar adalah kasus khusus dari distribusi normal di mana rata-rata adalah nol dan standar deviasi adalah 1. Distribusi ini juga dikenal sebagai distribusi Z.
Nilai pada distribusi normal standar dikenal sebagai skor standar atau skor-Z. Skor standar mewakili jumlah standar deviasi di atas atau di bawah rata -rata bahwa pengamatan spesifik jatuh. Misalnya, skor standar 1,5 menunjukkan bahwa pengamatan adalah 1,5 standar deviasi di atas rata -rata. Di sisi lain, skor negatif mewakili nilai di bawah rata -rata. Rata-rata memiliki skor-Z 0.
Grafik yang menampilkan distribusi normal standar.
Misalkan Anda menimbang apel dan beratnya 110 gram. Tidak ada cara untuk mengetahui dari berat saja bagaimana apel ini dibandingkan dengan apel lainnya. Namun, seperti yang akan Anda lihat, setelah Anda menghitung skor-Z, Anda tahu di mana ia jatuh relatif terhadap apel lainnya. Standardisasi: Cara menghitung skor-z
Skor standar adalah cara yang bagus untuk memahami di mana pengamatan spesifik jatuh relatif terhadap seluruh distribusi. Mereka juga memungkinkan Anda untuk melakukan pengamatan yang diambil dari populasi yang didistribusikan secara normal yang memiliki cara dan standar deviasi yang berbeda dan menempatkannya pada skala standar. Skala standar ini memungkinkan Anda untuk membandingkan pengamatan yang seharusnya sulit.
Proses ini disebut standardisasi, dan memungkinkan Anda untuk membandingkan pengamatan dan menghitung probabilitas di berbagai populasi. Dengan kata lain, ini memungkinkan Anda untuk membandingkan apel dengan jeruk. Bukan statistik yang bagus!
Untuk menstandarkan data Anda, Anda perlu mengubah pengukuran mentah menjadi skor-z.
Untuk menghitung skor standar untuk pengamatan, ambil pengukuran mentah, kurangi rata -rata, dan bagi dengan standar deviasi. Secara matematis, formula untuk proses itu adalah sebagai berikut:
Z = { displaystyle frac { text {x} - mu} { sigma}}
X mewakili nilai mentah dari pengukuran bunga. MU dan Sigma mewakili parameter untuk populasi dari mana pengamatan diambil.
Setelah Anda menstandarkan data Anda, Anda dapat menempatkannya dalam distribusi normal standar. Dengan cara ini, standardisasi memungkinkan Anda untuk membandingkan berbagai jenis pengamatan berdasarkan di mana setiap pengamatan termasuk dalam distribusinya sendiri. Contoh menggunakan skor standar untuk membuat perbandingan apel dengan jeruk
Misalkan kita benar -benar ingin membandingkan apel dengan jeruk. Secara khusus, mari kita bandingkan bobotnya. Bayangkan bahwa kami memiliki apel yang beratnya 110 gram dan jeruk yang beratnya 100 gram.
Jika kita membandingkan nilai -nilai mentah, mudah untuk melihat bahwa apel lebih berat daripada jeruk. Namun, mari kita bandingkan skor standar mereka. Untuk melakukan ini, kita perlu mengetahui sifat -sifat distribusi berat untuk apel dan jeruk. Asumsikan bahwa bobot apel dan jeruk mengikuti distribusi normal dengan nilai parameter berikut: apel jeruk rata -rata gram bobot 100 140 standar deviasi 15 25
Sekarang kami akan menghitung skor-z:
Apple = 110-100/15 = 0.667
Orange = 100-140/25 = -1.6
SCOR Z untuk apel (0,667) positif, yang berarti bahwa apel kami memiliki berat lebih dari rata-rata apel. Ini bukan nilai ekstrem dengan cara apa pun, tetapi di atas rata -rata untuk apel. Di sisi lain, oranye memiliki skor-Z yang cukup negatif (-1.6). Cukup jauh di bawah berat rata -rata untuk jeruk. Saya telah menempatkan nilai-z ini dalam distribusi normal standar di bawah ini.
Grafik distribusi normal standar yang membandingkan apel dengan jeruk menggunakan skor-z.
Sementara apel kami memiliki berat lebih dari oranye kami, kami membandingkan apel yang agak lebih berat dari rata -rata dengan oranye kecil yang lemah! Menggunakan skor-z, kami telah belajar bagaimana setiap buah sesuai dengan distribusinya sendiri dan bagaimana mereka membandingkan satu sama lain. Menemukan area di bawah kurva distribusi normal
Distribusi normal adalah distribusi probabilitas. Seperti halnya distribusi probabilitas apa pun, proporsi area yang berada di bawah kurva antara dua titik pada plot distribusi probabilitas menunjukkan probabilitas bahwa nilai akan termasuk dalam interval tersebut. Untuk mempelajari lebih lanjut tentang properti ini, baca posting saya tentang memahami distribusi probabilitas.
Biasanya, saya menggunakan perangkat lunak statistik untuk menemukan area di bawah kurva. Namun, ketika Anda bekerja dengan distribusi normal dan mengonversi nilai ke skor standar, Anda dapat menghitung area dengan mencari skor-z dalam tabel distribusi normal standar.
Karena ada jumlah yang tak terbatas dari distribusi normal yang berbeda, penerbit tidak dapat mencetak tabel untuk setiap distribusi. Namun, Anda dapat mengubah nilai dari distribusi normal apa pun menjadi skor-z, dan kemudian menggunakan tabel skor standar untuk menghitung probabilitas. Menggunakan tabel z-skor
Mari kita ambil skor-Z untuk apel kita (0,667) dan gunakan untuk menentukan persentil beratnya. Persentil adalah proporsi populasi yang berada di bawah nilai tertentu. Akibatnya, untuk menentukan persentil, kita perlu menemukan area yang sesuai dengan kisaran skor-z yang kurang dari 0,667. Di bagian tabel di bawah ini, skor-Z terdekat dengan kami adalah 0,65, yang akan kami gunakan.
Foto menunjukkan sebagian dari tabel skor standar (skor-z).
Trik dengan tabel ini adalah menggunakan nilai -nilai bersamaan dengan sifat -sifat distribusi normal untuk menghitung probabilitas yang Anda butuhkan. Nilai tabel menunjukkan bahwa luas kurva antara -0,65 dan +0,65 adalah 48,43%. Namun, bukan itu yang ingin kita ketahui. Kami menginginkan area yang kurang dari skor-Z 0,65.
Kita tahu bahwa dua bagian dari distribusi normal adalah gambar cermin satu sama lain. Jadi, jika area untuk interval dari -0,65 dan +0,65 adalah 48,43%, maka kisaran dari 0 hingga +0,65 harus setengah dari itu: 48,43/2 = 24,215%. Selain itu, kita tahu bahwa area untuk semua skor kurang dari nol adalah setengah (50%) dari distribusi.
Oleh karena itu, area untuk semua skor hingga 0,65 = 50% + 24.215% = 74.215%
Apple kami berada di sekitar persentil ke -74.
Di bawah ini adalah plot distribusi probabilitas yang dihasilkan oleh perangkat lunak statistik yang menunjukkan persentil yang sama bersama dengan representasi grafis dari area yang sesuai di bawah kurva. Nilainya sedikit berbeda karena kami menggunakan skor-Z 0,65 dari tabel sementara perangkat lunak menggunakan nilai yang lebih tepat dari 0,667.
Plot distribusi probabilitas yang secara grafis menampilkan persentil menggunakan skor-Z. Alasan lain mengapa distribusi normal itu penting
Selain semua hal di atas, ada beberapa alasan lain mengapa distribusi normal sangat penting dalam statistik.
Some statistical hypothesis tests assume that the data follow a normal distribution. However, as I explain in my post about parametric and nonparametric tests, there’s more to it than only whether the data are normally distributed.
Linear and nonlinear regression both assume that the residuals follow a normal distribution. Learn more in my post about assessing residual plots.
The central limit theorem states that as the sample size increases, the sampling distribution of the mean follows a normal distribution even when the underlying distribution of the original variable is non-normal.
Itu cukup sedikit tentang distribusi normal! Mudah -mudahan, Anda dapat memahami bahwa ini sangat penting karena banyak cara yang digunakan para analis.
Sumber: https://statisticsbyjim.com/basics/normal-distribution/

Probabilitas kumulatif dari distribusi normal dengan nilai yang diharapkan 0 dan standar deviasi 1: 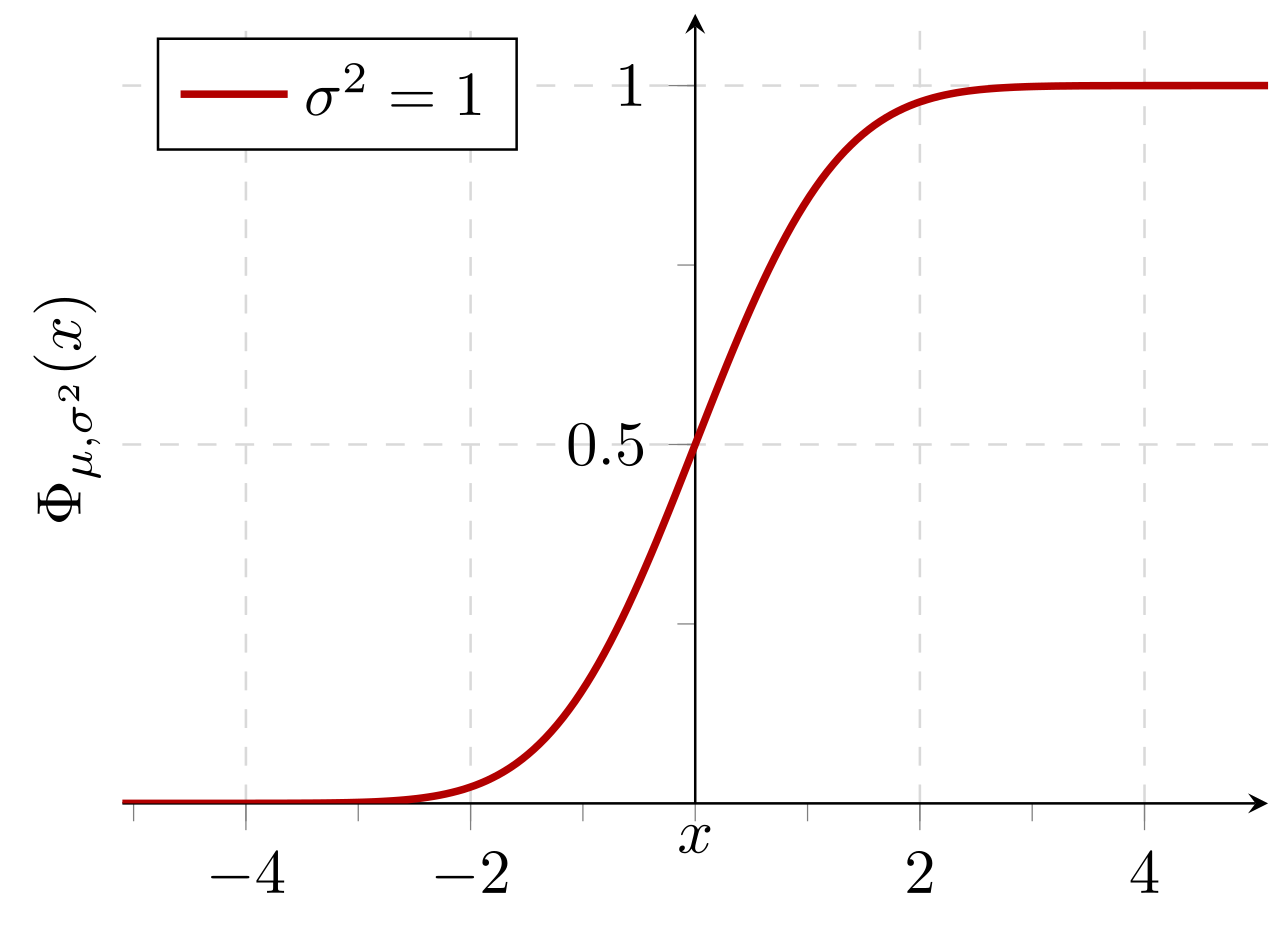
Ini adalah perangkat lunak gratis dan tidak terbebani yang dirilis ke domain publik - lihat file lisensi untuk detailnya.
Dibuat dengan ❤️ oleh Javier Cañon.