SQL Server Distribution ปกติ Gauss หรือ Bell Curve
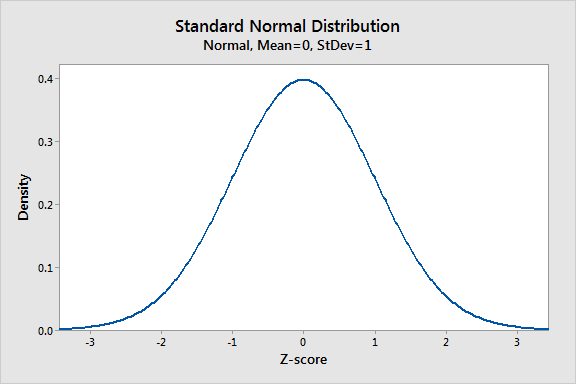
การแจกแจงแบบปกติคือการกระจายความน่าจะเป็นที่สำคัญที่สุดในสถิติเนื่องจากเหมาะกับปรากฏการณ์ทางธรรมชาติมากมาย ตัวอย่างเช่นความสูงความดันโลหิตข้อผิดพลาดการวัดและคะแนน IQ เป็นไปตามการกระจายปกติ มันยังเป็นที่รู้จักกันในชื่อการกระจายแบบเกาส์และเส้นโค้งระฆัง
การแจกแจงแบบปกติเป็นฟังก์ชันความน่าจะเป็นที่อธิบายถึงวิธีการกระจายค่าของตัวแปร มันเป็นการกระจายแบบสมมาตรที่กลุ่มการสังเกตส่วนใหญ่รอบจุดสูงสุดกลางและความน่าจะเป็นสำหรับค่าที่ไกลออกไปจากค่าเฉลี่ยเรียวออกอย่างเท่าเทียมกันในทั้งสองทิศทาง ค่าสุดขีดในทั้งสองหางของการแจกแจงนั้นไม่น่าเป็นไปได้เช่นเดียวกัน
ในโพสต์บล็อกนี้คุณจะได้เรียนรู้วิธีการใช้การกระจายปกติพารามิเตอร์และวิธีการคำนวณคะแนน Z เพื่อสร้างมาตรฐานข้อมูลของคุณและค้นหาความน่าจะเป็น ตัวอย่างของข้อมูลที่กระจายตามปกติ: ความสูง
ข้อมูลความสูงมักจะกระจาย การกระจายในตัวอย่างนี้เหมาะกับข้อมูลจริงที่ฉันรวบรวมจากเด็กหญิงอายุ 14 ปีในระหว่างการศึกษา
การกระจายความสูงปกติ
อย่างที่คุณเห็นการกระจายความสูงเป็นไปตามรูปแบบทั่วไปสำหรับการแจกแจงปกติทั้งหมด ผู้หญิงส่วนใหญ่อยู่ใกล้กับค่าเฉลี่ย (1.512 เมตร) ความแตกต่างเล็กน้อยระหว่างความสูงของแต่ละบุคคลและค่าเฉลี่ยเกิดขึ้นบ่อยกว่าการเบี่ยงเบนที่สำคัญจากค่าเฉลี่ย ค่าเบี่ยงเบนมาตรฐานคือ 0.0741m ซึ่งบ่งชี้ถึงระยะทางทั่วไปที่เด็กผู้หญิงแต่ละคนมักจะตกจากความสูงเฉลี่ย
การกระจายเป็นสมมาตร จำนวนผู้หญิงที่สั้นกว่าค่าเฉลี่ยเท่ากับจำนวนสาวที่สูงกว่าค่าเฉลี่ย ในทั้งสองหางของการแจกจ่ายผู้หญิงสั้นมากเกิดขึ้นไม่บ่อยนักเหมือนผู้หญิงที่สูงมาก พารามิเตอร์ของการแจกแจงปกติ
เช่นเดียวกับการแจกแจงความน่าจะเป็นพารามิเตอร์สำหรับการแจกแจงแบบปกติจะกำหนดรูปร่างและความน่าจะเป็นทั้งหมด การแจกแจงแบบปกติมีพารามิเตอร์สองตัวคือค่าเฉลี่ยและค่าเบี่ยงเบนมาตรฐาน การแจกแจงแบบปกติไม่ได้มีเพียงรูปแบบเดียว แต่รูปร่างจะเปลี่ยนไปตามค่าพารามิเตอร์ดังที่แสดงในกราฟด้านล่าง หมายถึง
ค่าเฉลี่ยคือแนวโน้มกลางของการกระจาย มันกำหนดตำแหน่งของจุดสูงสุดสำหรับการแจกแจงปกติ ค่าส่วนใหญ่คลัสเตอร์รอบค่าเฉลี่ย บนกราฟการเปลี่ยนค่าเฉลี่ยจะเปลี่ยนเส้นโค้งทั้งหมดซ้ายหรือขวาบนแกน x
กราฟที่แสดงการแจกแจงแบบปกติด้วยวิธีการที่แตกต่างกัน ค่าเบี่ยงเบนมาตรฐาน
ค่าเบี่ยงเบนมาตรฐานคือการวัดความแปรปรวน มันกำหนดความกว้างของการแจกแจงปกติ ค่าเบี่ยงเบนมาตรฐานกำหนดว่าค่าเฉลี่ยของค่ามักจะลดลง มันแสดงถึงระยะห่างทั่วไประหว่างการสังเกตและค่าเฉลี่ย
บนกราฟการเปลี่ยนค่าเบี่ยงเบนมาตรฐานไม่ว่าจะกระชับหรือกระจายความกว้างของการกระจายไปตามแกน x ค่าเบี่ยงเบนมาตรฐานที่ใหญ่ขึ้นผลิตการแจกแจงที่กระจายออกไปมากขึ้น
กราฟที่แสดงการแจกแจงแบบปกติที่มีค่าเบี่ยงเบนมาตรฐานที่แตกต่างกัน
เมื่อคุณมีการแจกแจงแบบแคบ ๆ ความน่าจะเป็นสูงกว่าที่ค่าจะไม่ตกอยู่ไกลจากค่าเฉลี่ย เมื่อคุณเพิ่มการแพร่กระจายของการกระจายความเป็นไปได้ที่การสังเกตจะอยู่ห่างจากค่าเฉลี่ยเพิ่มขึ้นเช่นกัน พารามิเตอร์ประชากรเมื่อเทียบกับการประมาณตัวอย่าง
ค่าเฉลี่ยและค่าเบี่ยงเบนมาตรฐานคือค่าพารามิเตอร์ที่ใช้กับประชากรทั้งหมด สำหรับการแจกแจงแบบปกตินักสถิติมีความหมายถึงพารามิเตอร์โดยใช้สัญลักษณ์กรีกμ (MU) สำหรับค่าเฉลี่ยประชากรและσ (ซิกมา) สำหรับค่าเบี่ยงเบนมาตรฐานประชากร
น่าเสียดายที่พารามิเตอร์ประชากรมักไม่เป็นที่รู้จักเพราะโดยทั่วไปแล้วเป็นไปไม่ได้ที่จะวัดประชากรทั้งหมด อย่างไรก็ตามคุณสามารถใช้ตัวอย่างแบบสุ่มเพื่อคำนวณการประมาณค่าพารามิเตอร์เหล่านี้ นักสถิติแสดงถึงการประมาณตัวอย่างของพารามิเตอร์เหล่านี้โดยใช้X̅สำหรับค่าเฉลี่ยตัวอย่างและ S สำหรับค่าเบี่ยงเบนมาตรฐานตัวอย่าง
โพสต์ที่เกี่ยวข้อง: มาตรการของแนวโน้มกลางและมาตรการของความแปรปรวนคุณสมบัติทั่วไปสำหรับทุกรูปแบบของการกระจายปกติ
แม้จะมีรูปร่างที่แตกต่างกัน แต่รูปแบบของการแจกแจงแบบปกติทุกรูปแบบมีคุณสมบัติลักษณะดังต่อไปนี้
They’re all symmetric. The normal distribution cannot model skewed distributions.
The mean, median, and mode are all equal.
Half of the population is less than the mean and half is greater than the mean.
The Empirical Rule allows you to determine the proportion of values that fall within certain distances from the mean. More on this below!
ในขณะที่การกระจายปกติเป็นสิ่งจำเป็นในสถิติ แต่ก็เป็นเพียงหนึ่งในการแจกแจงความน่าจะเป็นจำนวนมากและไม่พอดีกับประชากรทั้งหมด หากต้องการเรียนรู้วิธีการตรวจสอบว่าการแจกแจงแบบปกตินั้นเหมาะสมที่สุดกับข้อมูลตัวอย่างของคุณอ่านโพสต์ของฉันเกี่ยวกับวิธีการระบุการกระจายข้อมูลของคุณและการประเมินค่าปกติ: ฮิสโตแกรมกับแปลงความน่าจะเป็นปกติ กฎเชิงประจักษ์สำหรับการแจกแจงแบบปกติ
เมื่อคุณมีข้อมูลกระจายตามปกติค่าเบี่ยงเบนมาตรฐานจะมีค่าเป็นพิเศษ คุณสามารถใช้เพื่อกำหนดสัดส่วนของค่าที่อยู่ภายในจำนวนเบี่ยงเบนมาตรฐานที่ระบุจากค่าเฉลี่ย ตัวอย่างเช่นในการกระจายปกติ 68% ของการสังเกตอยู่ภายใน +/- 1 ส่วนเบี่ยงเบนมาตรฐานจากค่าเฉลี่ย คุณสมบัตินี้เป็นส่วนหนึ่งของกฎเชิงประจักษ์ซึ่งอธิบายเปอร์เซ็นต์ของข้อมูลที่อยู่ในจำนวนเบี่ยงเบนมาตรฐานที่เฉพาะเจาะจงจากค่าเฉลี่ยสำหรับเส้นโค้งรูประฆัง ค่าเฉลี่ย +/- อัตราการเบี่ยงเบนมาตรฐานของข้อมูลที่มี 1 68% 2 95% 3 99.7%
ลองดูตัวอย่างการจัดส่งพิซซ่า สมมติว่าร้านอาหารพิซซ่ามีเวลาจัดส่งเฉลี่ย 30 นาทีและเบี่ยงเบนมาตรฐาน 5 นาที การใช้กฎเชิงประจักษ์เราสามารถระบุได้ว่า 68% ของเวลาส่งมอบระหว่าง 25-35 นาที (30 +/- 5) 95% อยู่ระหว่าง 20-40 นาที (30 +/- 2 5) และ 99.7% อยู่ระหว่าง 15-45 นาที (30 +/- 3 5) แผนภูมิด้านล่างแสดงคุณสมบัตินี้แบบกราฟิก
กราฟที่แสดงการกระจายปกติกับพื้นที่หารด้วยส่วนเบี่ยงเบนมาตรฐาน การกระจายปกติมาตรฐานและคะแนนมาตรฐาน
ดังที่เราได้เห็นข้างต้นการแจกแจงแบบปกติมีรูปร่างที่แตกต่างกันมากมายขึ้นอยู่กับค่าพารามิเตอร์ อย่างไรก็ตามการแจกแจงปกติมาตรฐานเป็นกรณีพิเศษของการแจกแจงปกติที่ค่าเฉลี่ยเป็นศูนย์และค่าเบี่ยงเบนมาตรฐานคือ 1 การแจกแจงนี้เรียกว่าการกระจาย Z
ค่าในการแจกแจงปกติมาตรฐานเรียกว่าคะแนนมาตรฐานหรือคะแนน Z คะแนนมาตรฐานแสดงถึงจำนวนของค่าเบี่ยงเบนมาตรฐานด้านบนหรือต่ำกว่าค่าเฉลี่ยที่การสังเกตที่เฉพาะเจาะจงลดลง ตัวอย่างเช่นคะแนนมาตรฐาน 1.5 บ่งชี้ว่าการสังเกตคือ 1.5 ส่วนเบี่ยงเบนมาตรฐานเหนือค่าเฉลี่ย ในทางกลับกันคะแนนลบแสดงถึงค่าต่ำกว่าค่าเฉลี่ย ค่าเฉลี่ยมีคะแนน Z เท่ากับ 0
กราฟที่แสดงการกระจายปกติมาตรฐาน
สมมติว่าคุณมีน้ำหนักแอปเปิ้ลและมีน้ำหนัก 110 กรัม ไม่มีวิธีที่จะบอกได้จากน้ำหนักเพียงอย่างเดียวแอปเปิ้ลนี้เปรียบเทียบกับแอปเปิ้ลอื่น ๆ ได้อย่างไร อย่างไรก็ตามอย่างที่คุณเห็นหลังจากที่คุณคำนวณคะแนน Z คุณจะรู้ว่ามันอยู่ตรงไหนเมื่อเทียบกับแอปเปิ้ลอื่น ๆ มาตรฐาน: วิธีการคำนวณคะแนน Z
คะแนนมาตรฐานเป็นวิธีที่ดีในการทำความเข้าใจว่าการสังเกตที่เฉพาะเจาะจงนั้นเกี่ยวข้องกับการกระจายทั้งหมด พวกเขายังอนุญาตให้คุณทำการสังเกตจากประชากรที่กระจายตามปกติซึ่งมีวิธีการที่แตกต่างกันและส่วนเบี่ยงเบนมาตรฐานและวางไว้ในระดับมาตรฐาน มาตราส่วนมาตรฐานนี้ช่วยให้คุณเปรียบเทียบการสังเกตที่อาจเป็นเรื่องยาก
กระบวนการนี้เรียกว่ามาตรฐานและช่วยให้คุณสามารถเปรียบเทียบการสังเกตและคำนวณความน่าจะเป็นในประชากรที่แตกต่างกัน กล่าวอีกนัยหนึ่งมันอนุญาตให้คุณเปรียบเทียบแอปเปิ้ลกับส้ม สถิติไม่ดี!
ในการสร้างมาตรฐานข้อมูลของคุณคุณต้องแปลงการวัดดิบเป็นคะแนน z
ในการคำนวณคะแนนมาตรฐานสำหรับการสังเกตใช้การวัดดิบลบค่าเฉลี่ยและหารด้วยค่าเบี่ยงเบนมาตรฐาน คณิตศาสตร์สูตรสำหรับกระบวนการนั้นมีดังต่อไปนี้:
z = { displaystyle frac { text {x} - mu} { sigma}}
x หมายถึงมูลค่าดิบของการวัดดอกเบี้ย MU และ Sigma เป็นตัวแทนของพารามิเตอร์สำหรับประชากรที่มีการสังเกต
หลังจากที่คุณสร้างมาตรฐานข้อมูลของคุณแล้วคุณสามารถวางไว้ในการแจกแจงแบบปกติมาตรฐาน ในลักษณะนี้มาตรฐานช่วยให้คุณสามารถเปรียบเทียบการสังเกตประเภทต่าง ๆ ตามที่การสังเกตแต่ละครั้งตกอยู่ในการแจกแจงของตัวเอง ตัวอย่างของการใช้คะแนนมาตรฐานในการเปรียบเทียบแอปเปิ้ลกับส้มเปรียบเทียบ
สมมติว่าเราต้องการเปรียบเทียบแอปเปิ้ลกับส้มอย่างแท้จริง โดยเฉพาะลองเปรียบเทียบน้ำหนักของพวกเขา ลองนึกภาพว่าเรามีแอปเปิ้ลที่มีน้ำหนัก 110 กรัมและส้มที่มีน้ำหนัก 100 กรัม
หากเราเปรียบเทียบค่าดิบมันเป็นเรื่องง่ายที่จะเห็นว่าแอปเปิ้ลมีน้ำหนักมากกว่าสีส้ม อย่างไรก็ตามลองเปรียบเทียบคะแนนมาตรฐานของพวกเขา ในการทำเช่นนี้เราจะต้องรู้คุณสมบัติของการกระจายน้ำหนักสำหรับแอปเปิ้ลและส้ม สมมติว่าน้ำหนักของแอปเปิ้ลและส้มติดตามการแจกแจงแบบปกติด้วยค่าพารามิเตอร์ต่อไปนี้: แอปเปิ้ลส้มเฉลี่ยน้ำหนักกรัม 100 140 เบี่ยงเบนมาตรฐาน 15 25 25 25 25 25 25 25 25 25 25 25 25
ตอนนี้เราจะคำนวณคะแนน z:
Apple = 110-100/15 = 0.667
Orange = 100-140/25 = -1.6
คะแนน Z สำหรับแอปเปิ้ล (0.667) เป็นค่าบวกซึ่งหมายความว่าแอปเปิ้ลของเรามีน้ำหนักมากกว่าแอปเปิ้ลเฉลี่ย มันไม่ได้มีค่ามาก แต่ก็สูงกว่าค่าเฉลี่ยสำหรับแอปเปิ้ล ในทางกลับกันสีส้มมีคะแนน Z เชิงลบ (-1.6) มันค่อนข้างต่ำกว่าน้ำหนักเฉลี่ยสำหรับส้ม ฉันได้วางค่า z เหล่านี้ไว้ในการกระจายปกติมาตรฐานด้านล่าง
กราฟของการแจกแจงปกติมาตรฐานที่เปรียบเทียบแอปเปิ้ลกับส้มโดยใช้คะแนน Z
ในขณะที่แอปเปิ้ลของเรามีน้ำหนักมากกว่าสีส้มของเรา แต่เรากำลังเปรียบเทียบแอปเปิ้ลที่ค่อนข้างหนักกว่าค่าเฉลี่ยกับส้มที่น่าพิศวง! การใช้คะแนน Z เราได้เรียนรู้ว่าผลไม้แต่ละชนิดเหมาะสมอย่างไรในการกระจายของตัวเองและวิธีการเปรียบเทียบซึ่งกันและกัน การค้นหาพื้นที่ภายใต้เส้นโค้งของการกระจายปกติ
การกระจายปกติคือการกระจายความน่าจะเป็น เช่นเดียวกับการกระจายความน่าจะเป็นสัดส่วนของพื้นที่ที่อยู่ภายใต้เส้นโค้งระหว่างสองจุดบนพล็อตการแจกแจงความน่าจะเป็นบ่งชี้ถึงความน่าจะเป็นที่ค่าจะอยู่ภายในช่วงเวลานั้น หากต้องการเรียนรู้เพิ่มเติมเกี่ยวกับคุณสมบัตินี้อ่านโพสต์ของฉันเกี่ยวกับการทำความเข้าใจการแจกแจงความน่าจะเป็น
โดยทั่วไปฉันใช้ซอฟต์แวร์ทางสถิติเพื่อค้นหาพื้นที่ภายใต้เส้นโค้ง อย่างไรก็ตามเมื่อคุณทำงานกับการแจกแจงแบบปกติและแปลงค่าเป็นคะแนนมาตรฐานคุณสามารถคำนวณพื้นที่ได้โดยค้นหาคะแนน Z ในตารางการแจกแจงปกติมาตรฐาน
เนื่องจากมีจำนวนการแจกแจงปกติที่แตกต่างกันจำนวน จำกัด ผู้เผยแพร่จึงไม่สามารถพิมพ์ตารางสำหรับการแจกแจงแต่ละครั้ง อย่างไรก็ตามคุณสามารถแปลงค่าจากการแจกแจงปกติเป็นคะแนน z จากนั้นใช้ตารางคะแนนมาตรฐานเพื่อคำนวณความน่าจะเป็น ใช้ตารางคะแนน Z
ลองใช้คะแนน Z สำหรับแอปเปิ้ลของเรา (0.667) และใช้เพื่อกำหนดเปอร์เซ็นต์น้ำหนัก เปอร์เซ็นไทล์คือสัดส่วนของประชากรที่ต่ำกว่าค่าเฉพาะ ดังนั้นเพื่อกำหนดเปอร์เซ็นไทล์เราจำเป็นต้องค้นหาพื้นที่ที่สอดคล้องกับช่วงของคะแนน Z ที่น้อยกว่า 0.667 ในส่วนของตารางด้านล่างคะแนน Z ที่ใกล้เคียงที่สุดสำหรับเราคือ 0.65 ซึ่งเราจะใช้
ภาพถ่ายแสดงส่วนหนึ่งของตารางคะแนนมาตรฐาน (คะแนน Z)
เคล็ดลับกับตารางเหล่านี้คือการใช้ค่าร่วมกับคุณสมบัติของการแจกแจงแบบปกติเพื่อคำนวณความน่าจะเป็นที่คุณต้องการ ค่าตารางระบุว่าพื้นที่ของเส้นโค้งระหว่าง -0.65 และ +0.65 คือ 48.43% อย่างไรก็ตามนั่นไม่ใช่สิ่งที่เราอยากรู้ เราต้องการพื้นที่ที่น้อยกว่าคะแนน Z ที่ 0.65
เรารู้ว่าทั้งสองครึ่งของการแจกแจงแบบปกติเป็นภาพสะท้อนของกันและกัน ดังนั้นหากพื้นที่สำหรับช่วงเวลาตั้งแต่ -0.65 และ +0.65 คือ 48.43%ดังนั้นช่วงตั้งแต่ 0 ถึง +0.65 จะต้องครึ่งหนึ่งของที่: 48.43/2 = 24.215% นอกจากนี้เรารู้ว่าพื้นที่สำหรับคะแนนทั้งหมดน้อยกว่าศูนย์คือครึ่ง (50%) ของการกระจาย
ดังนั้นพื้นที่สำหรับคะแนนทั้งหมดสูงถึง 0.65 = 50% + 24.215% = 74.215%
แอปเปิ้ลของเราอยู่ที่ประมาณร้อยละ 74
ด้านล่างเป็นพล็อตการกระจายความน่าจะเป็นที่ผลิตโดยซอฟต์แวร์ทางสถิติที่แสดงเปอร์เซ็นไทล์เดียวกันพร้อมกับการแสดงกราฟิกของพื้นที่ที่สอดคล้องกันภายใต้เส้นโค้ง ค่าแตกต่างกันเล็กน้อยเนื่องจากเราใช้คะแนน Z 0.65 จากตารางในขณะที่ซอฟต์แวร์ใช้ค่าที่แม่นยำมากขึ้น 0.667
พล็อตการแจกแจงความน่าจะเป็นที่แสดงเปอร์เซ็นต์ไทล์โดยใช้คะแนน Z เหตุผลอื่น ๆ ว่าทำไมการกระจายปกติจึงมีความสำคัญ
นอกเหนือจากทั้งหมดข้างต้นแล้วยังมีเหตุผลอื่น ๆ อีกหลายประการที่การแจกแจงแบบปกติมีความสำคัญในสถิติ
Some statistical hypothesis tests assume that the data follow a normal distribution. However, as I explain in my post about parametric and nonparametric tests, there’s more to it than only whether the data are normally distributed.
Linear and nonlinear regression both assume that the residuals follow a normal distribution. Learn more in my post about assessing residual plots.
The central limit theorem states that as the sample size increases, the sampling distribution of the mean follows a normal distribution even when the underlying distribution of the original variable is non-normal.
นั่นค่อนข้างเกี่ยวกับการกระจายปกติ! หวังว่าคุณจะเข้าใจว่ามันสำคัญมากเพราะหลายวิธีที่นักวิเคราะห์ใช้
ที่มา: https://statisticsbyjim.com/basics/normal-distribution/

ความน่าจะเป็นสะสมของการแจกแจงปกติด้วยค่าที่คาดหวัง 0 และค่าเบี่ยงเบนมาตรฐาน 1: 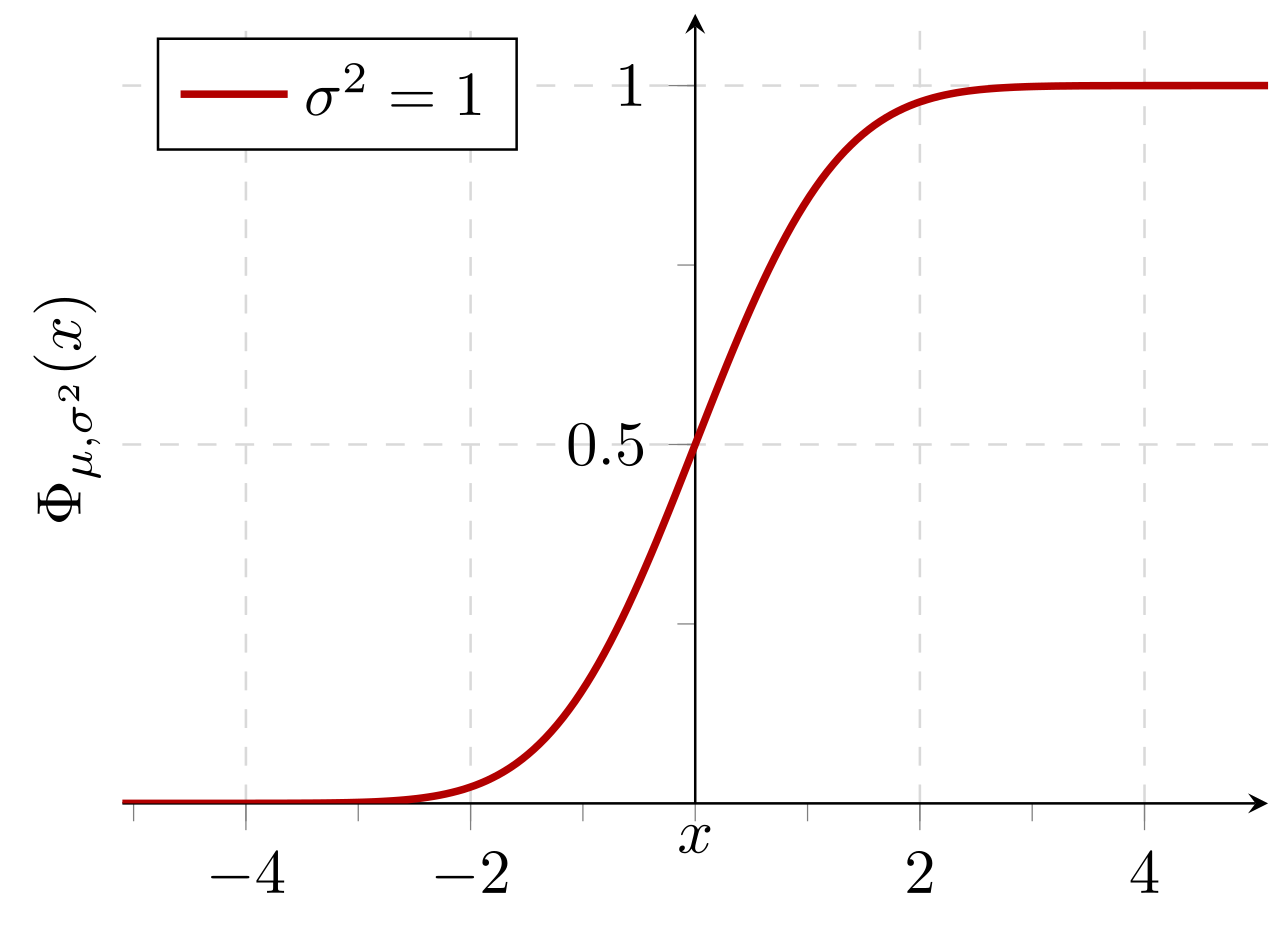
นี่คือซอฟต์แวร์ฟรีและไม่ได้รับการเผยแพร่ในโดเมนสาธารณะ - ดูไฟล์ใบอนุญาตสำหรับรายละเอียด
ทำด้วย❤โดย Javier Cañon