SQL Server Normal Distribution, Gauss ou Bell Curve
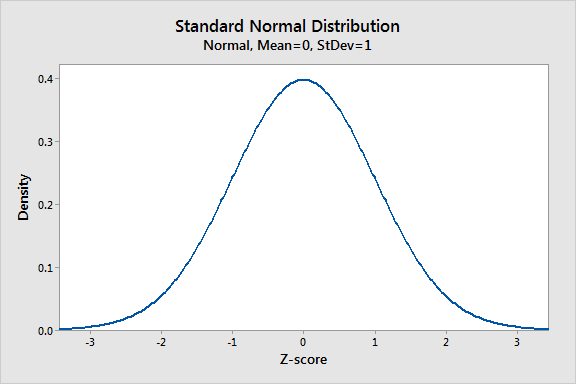
La distribution normale est la distribution de probabilité la plus importante dans les statistiques car elle correspond à de nombreux phénomènes naturels. Par exemple, les hauteurs, la pression artérielle, l'erreur de mesure et les scores de QI suivent la distribution normale. Il est également connu sous le nom de distribution gaussienne et de courbe de cloche.
La distribution normale est une fonction de probabilité qui décrit comment les valeurs d'une variable sont distribuées. Il s'agit d'une distribution symétrique où la plupart des observations se regroupent autour du pic central et les probabilités de valeurs plus éloignées du cône moyen éteint également dans les deux directions. Les valeurs extrêmes dans les deux queues de la distribution sont également peu probables.
Dans cet article de blog, vous apprendrez à utiliser la distribution normale, ses paramètres et comment calculer les scores Z pour normaliser vos données et trouver des probabilités. Exemple de données normalement distribuées: hauteurs
Les données de hauteur sont normalement distribuées. La distribution de cet exemple correspond aux données réelles que j'ai collectées auprès de filles de 14 ans lors d'une étude.
Distribution normale des hauteurs.
Comme vous pouvez le voir, la distribution des hauteurs suit le modèle typique pour toutes les distributions normales. La plupart des filles sont proches de la moyenne (1,512 mètres). De petites différences entre la hauteur d'un individu et la moyenne se produisent plus fréquemment que les écarts substantiels par rapport à la moyenne. L'écart type est de 0,0741 m, ce qui indique la distance typique que les filles individuelles ont tendance à tomber de la hauteur moyenne.
La distribution est symétrique. Le nombre de filles plus court que la moyenne est égal au nombre de filles plus hautes que la moyenne. Dans les deux queues de la distribution, les filles extrêmement courtes se produisent aussi rarement que des filles extrêmement hautes. Paramètres de la distribution normale
Comme pour toute distribution de probabilité, les paramètres de la distribution normale définissent entièrement sa forme et ses probabilités. La distribution normale a deux paramètres, la moyenne et l'écart type. La distribution normale n'a pas une seule forme. Au lieu de cela, la forme change en fonction des valeurs des paramètres, comme indiqué dans les graphiques ci-dessous. Signifier
La moyenne est la tendance centrale de la distribution. Il définit l'emplacement du pic pour les distributions normales. La plupart des valeurs se regroupent autour de la moyenne. Sur un graphique, la modification de la moyenne déplace la courbe entière à gauche ou à droite sur l'axe X.
Graphique qui affiche des distributions normales avec différents moyens. Écart-type
L'écart type est une mesure de la variabilité. Il définit la largeur de la distribution normale. L'écart type détermine à quelle distance de la moyenne des valeurs a tendance à tomber. Il représente la distance typique entre les observations et la moyenne.
Sur un graphique, la modification de l'écart type se resserre ou répartit la largeur de la distribution le long de l'axe x. Des écarts-types plus importants produisent des distributions plus étalées.
Graphique qui affiche des distributions normales avec différents écarts-types.
Lorsque vous avez des distributions étroites, les probabilités sont plus élevées que les valeurs ne tombent pas loin de la moyenne. Lorsque vous augmentez la propagation de la distribution, la probabilité que les observations soient plus éloignées de la moyenne augmente également. Paramètres de population par rapport aux estimations de l'échantillon
La moyenne et l'écart type sont les valeurs de paramètres qui s'appliquent aux populations entières. Pour la distribution normale, les statisticiens signifient les paramètres en utilisant le symbole grec μ (MU) pour la moyenne de la population et σ (Sigma) pour l'écart type de la population.
Malheureusement, les paramètres de population sont généralement inconnus car il est généralement impossible de mesurer une population entière. Cependant, vous pouvez utiliser des échantillons aléatoires pour calculer les estimations de ces paramètres. Les statisticiens représentent des estimations de l'échantillon de ces paramètres utilisant X̅ pour la moyenne de l'échantillon et S pour l'écart type de l'échantillon.
Posts connexes: Mesures de la tendance centrale et des mesures de la variabilité des propriétés communes pour toutes les formes de la distribution normale
Malgré les différentes formes, toutes les formes de la distribution normale ont les propriétés caractéristiques suivantes.
They’re all symmetric. The normal distribution cannot model skewed distributions.
The mean, median, and mode are all equal.
Half of the population is less than the mean and half is greater than the mean.
The Empirical Rule allows you to determine the proportion of values that fall within certain distances from the mean. More on this below!
Bien que la distribution normale soit essentielle dans les statistiques, ce n'est qu'une des nombreuses distributions de probabilité, et elle ne correspond pas à toutes les populations. Pour savoir comment déterminer si la distribution normale fournit le meilleur ajustement à vos exemples de données, lisez mes articles sur la façon d'identifier la distribution de vos données et d'évaluer la normalité: histogrammes par rapport aux parcelles de probabilité normales. La règle empirique pour la distribution normale
Lorsque vous avez normalement distribué des données, l'écart type devient particulièrement précieux. Vous pouvez l'utiliser pour déterminer la proportion des valeurs qui se situent dans un nombre spécifié d'écarts-types par rapport à la moyenne. Par exemple, dans une distribution normale, 68% des observations relèvent de +/- 1 écart type par rapport à la moyenne. Cette propriété fait partie de la règle empirique, qui décrit le pourcentage des données qui relèvent d'un nombre spécifique d'écarts-types par rapport à la moyenne des courbes en forme de cloche. Moyenne +/- écarts-types pourcentage de données contenues 1 68% 2 95% 3 99,7%
Regardons un exemple de livraison de pizza. Supposons qu'une pizza a un délai de livraison moyen de 30 minutes et un écart-type de 5 minutes. En utilisant la règle empirique, nous pouvons déterminer que 68% des délais de livraison sont comprises entre 25 et 35 minutes (30 +/- 5), 95% sont comprises entre 20 et 40 minutes (30 +/- 2 5) et 99,7% sont comprises entre 15 et 45 minutes (30 +/- 3 5). Le graphique ci-dessous illustre graphiquement cette propriété.
Graphique qui affiche une distribution normale avec des zones divisées par des écarts-types. Distribution normale standard et scores standard
Comme nous l'avons vu ci-dessus, la distribution normale a de nombreuses formes différentes en fonction des valeurs des paramètres. Cependant, la distribution normale standard est un cas particulier de la distribution normale où la moyenne est nulle et l'écart type est 1. Cette distribution est également connue sous le nom de distribution Z.
Une valeur sur la distribution normale standard est connue comme un score standard ou un score Z. Un score standard représente le nombre d'écarts-types au-dessus ou en dessous de la moyenne qu'une observation spécifique tombe. Par exemple, un score standard de 1,5 indique que l'observation est de 1,5 écarts-type au-dessus de la moyenne. D'un autre côté, un score négatif représente une valeur inférieure à la moyenne. La moyenne a un score z de 0.
Graphique qui affiche une distribution normale standard.
Supposons que vous pesiez une pomme et qu'il pèse 110 grammes. Il n'y a aucun moyen de dire à partir du poids seul comment cette pomme se compare aux autres pommes. Cependant, comme vous le verrez, après avoir calculé son score Z, vous savez où il tombe par rapport aux autres pommes. Standardisation: comment calculer les scores z
Les scores standard sont un excellent moyen de comprendre où une observation spécifique tombe par rapport à l'ensemble de la distribution. Ils vous permettent également de prendre des observations tirées de populations normalement distribuées qui ont des moyens et des écarts-types différents et les placer à une échelle standard. Cette échelle standard vous permet de comparer les observations qui seraient autrement difficiles.
Ce processus est appelé standardisation et vous permet de comparer les observations et de calculer les probabilités entre différentes populations. En d'autres termes, il vous permet de comparer les pommes aux oranges. Les statistiques ne sont-elles pas super!
Pour normaliser vos données, vous devez convertir les mesures brutes en z-scores.
Pour calculer le score standard pour une observation, prenez la mesure brute, soustrayez la moyenne et divisez par l'écart type. Mathématiquement, la formule de ce processus est la suivante:
Z = { displaystyle frac { text {x} - mu} { sigma}}
X représente la valeur brute de la mesure de l'intérêt. Mu et Sigma représentent les paramètres de la population à partir de laquelle l'observation a été tirée.
Après avoir standardisé vos données, vous pouvez les placer dans la distribution normale standard. De cette manière, la normalisation vous permet de comparer différents types d'observations en fonction de l'endroit où chaque observation relève de sa propre distribution. Exemple d'utilisation des scores standard pour faire une comparaison des pommes à Oranges
Supposons que nous voulons littéralement comparer les pommes aux oranges. Plus précisément, comparons leurs poids. Imaginez que nous avons une pomme qui pèse 110 grammes et une orange qui pèse 100 grammes.
Si nous comparons les valeurs brutes, il est facile de voir que la pomme pèse plus que l'orange. Cependant, comparons leurs scores standard. Pour ce faire, nous devrons connaître les propriétés des distributions de poids pour les pommes et les oranges. Supposons que les poids des pommes et des oranges suivent une distribution normale avec les valeurs de paramètre suivantes: pommes oranges de poids moyen Grams 100 140 écart type 15 25
Nous allons maintenant calculer les z-scores:
Apple = 110-100/15 = 0.667
Orange = 100-140/25 = -1.6
Le score Z pour la pomme (0,667) est positif, ce qui signifie que notre pomme pèse plus que la pomme moyenne. Ce n'est en aucun cas une valeur extrême, mais elle est supérieure à la moyenne pour les pommes. D'un autre côté, l'orange a un score Z assez négatif (-1,6). Il est assez loin en dessous du poids moyen des oranges. J'ai placé ces valeurs Z dans la distribution normale standard ci-dessous.
Graphique d'une distribution normale standard qui compare les pommes aux oranges à l'aide d'un score Z.
Alors que notre pomme pèse plus que notre orange, nous comparons une pomme quelque peu plus lourde que la moyenne à une orange carrément chétif! À l'aide de z-scores, nous avons appris comment chaque fruit s'inscrit dans sa propre distribution et comment ils se comparent les uns aux autres. Trouver des zones sous la courbe d'une distribution normale
La distribution normale est une distribution de probabilité. Comme pour toute distribution de probabilité, la proportion de la zone qui tombe sous la courbe entre deux points sur un tracé de distribution de probabilité indique la probabilité qu'une valeur se situera dans cet intervalle. Pour en savoir plus sur cette propriété, lisez mon article sur la compréhension des distributions de probabilité.
En règle générale, j'utilise un logiciel statistique pour trouver des zones sous la courbe. Cependant, lorsque vous travaillez avec la distribution normale et convertissez les valeurs en scores standard, vous pouvez calculer les zones en recherchant des scores Z dans un tableau de distribution normal standard.
Parce qu'il existe un nombre infini de distributions normales différentes, les éditeurs ne peuvent pas imprimer un tableau pour chaque distribution. Cependant, vous pouvez transformer les valeurs de n'importe quelle distribution normale en scores Z, puis utiliser un tableau des scores standard pour calculer les probabilités. Utilisation d'une table de z-scores
Prenons le score Z pour notre pomme (0,667) et utilisons-le pour déterminer son percentile de poids. Un centile est la proportion d'une population qui tombe en dessous d'une valeur spécifique. Par conséquent, pour déterminer le centile, nous devons trouver la zone qui correspond à la plage de scores Z inférieure à 0,667. Dans la partie du tableau ci-dessous, le score Z le plus proche du nôtre est de 0,65, que nous utiliserons.
La photographie montre une partie d'un tableau des scores standard (z-scores).
L'astuce avec ces tables consiste à utiliser les valeurs conjointement avec les propriétés de la distribution normale pour calculer la probabilité dont vous avez besoin. La valeur du tableau indique que l'aire de la courbe entre -0,65 et +0,65 est de 48,43%. Cependant, ce n'est pas ce que nous voulons savoir. Nous voulons la zone inférieure à un score Z de 0,65.
Nous savons que les deux moitiés de la distribution normale sont des images miroir les unes des autres. Ainsi, si l'aire de l'intervalle de -0,65 et +0,65 est de 48,43%, alors la plage de 0 à +0,65 doit être la moitié de cela: 48,43 / 2 = 24,215%. De plus, nous savons que la zone pour tous les scores inférieure à zéro est la moitié (50%) de la distribution.
Par conséquent, la zone pour tous les scores jusqu'à 0,65 = 50% + 24,215% = 74,215%
Notre pomme est à environ le 74e centile.
Vous trouverez ci-dessous un tracé de distribution de probabilité produit par un logiciel statistique qui montre le même centile ainsi qu'une représentation graphique de la zone correspondante sous la courbe. La valeur est légèrement différente car nous avons utilisé un score Z de 0,65 du tableau tandis que le logiciel utilise la valeur la plus précise de 0,667.
Un tracé de distribution de probabilité qui affiche graphiquement un centile à l'aide d'un score Z. Autres raisons pour lesquelles la distribution normale est importante
En plus de tout ce qui précède, il existe plusieurs autres raisons pour lesquelles la distribution normale est cruciale dans les statistiques.
Some statistical hypothesis tests assume that the data follow a normal distribution. However, as I explain in my post about parametric and nonparametric tests, there’s more to it than only whether the data are normally distributed.
Linear and nonlinear regression both assume that the residuals follow a normal distribution. Learn more in my post about assessing residual plots.
The central limit theorem states that as the sample size increases, the sampling distribution of the mean follows a normal distribution even when the underlying distribution of the original variable is non-normal.
C'était un peu sur la distribution normale! J'espère que vous pouvez comprendre que c'est crucial en raison des nombreuses façons dont les analystes l'utilisent.
Source: https://statisticsbyjim.com/basics/ormal-distribution/

Probabilité cumulée d'une distribution normale avec la valeur attendue 0 et l'écart type 1: 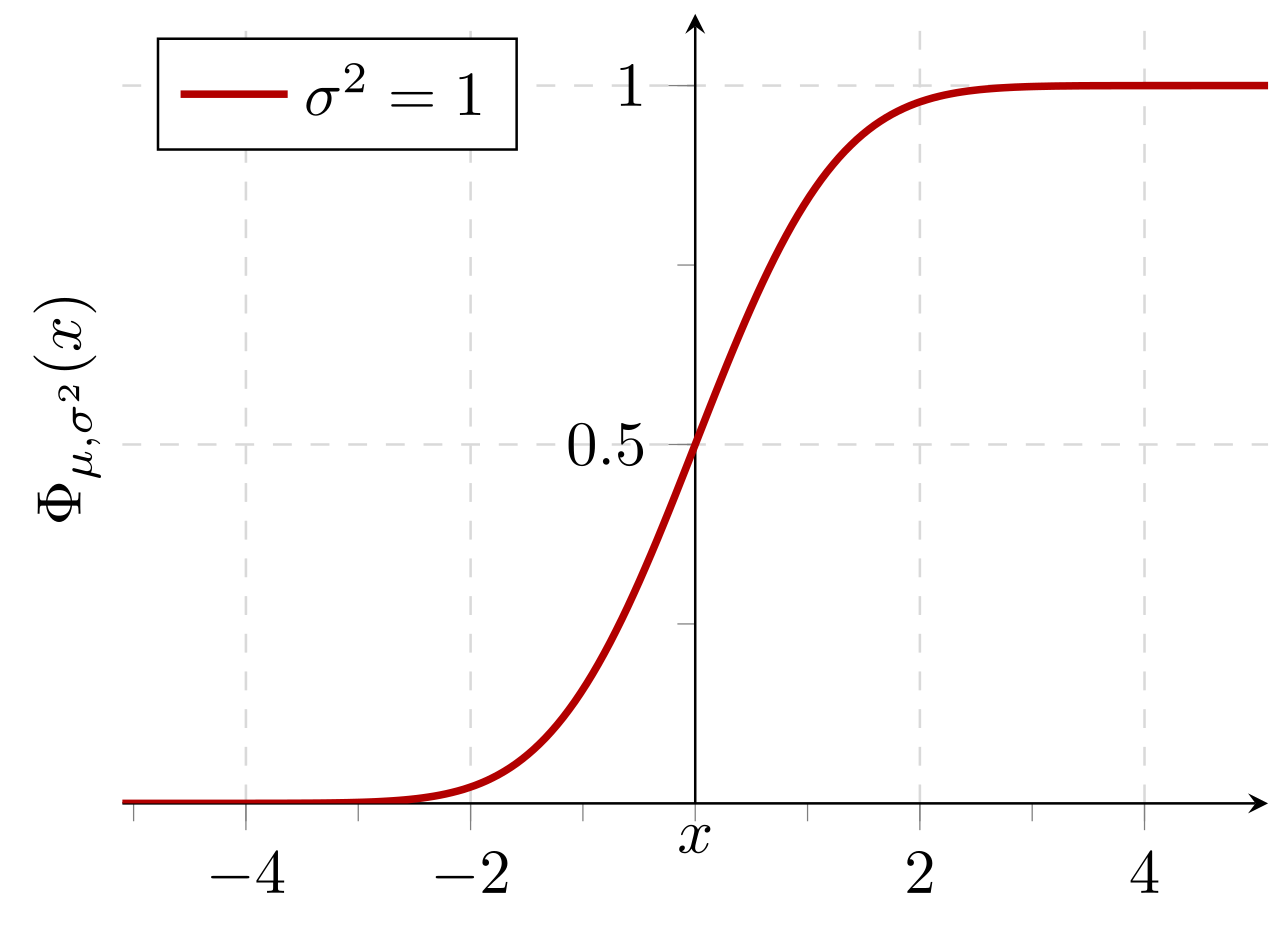
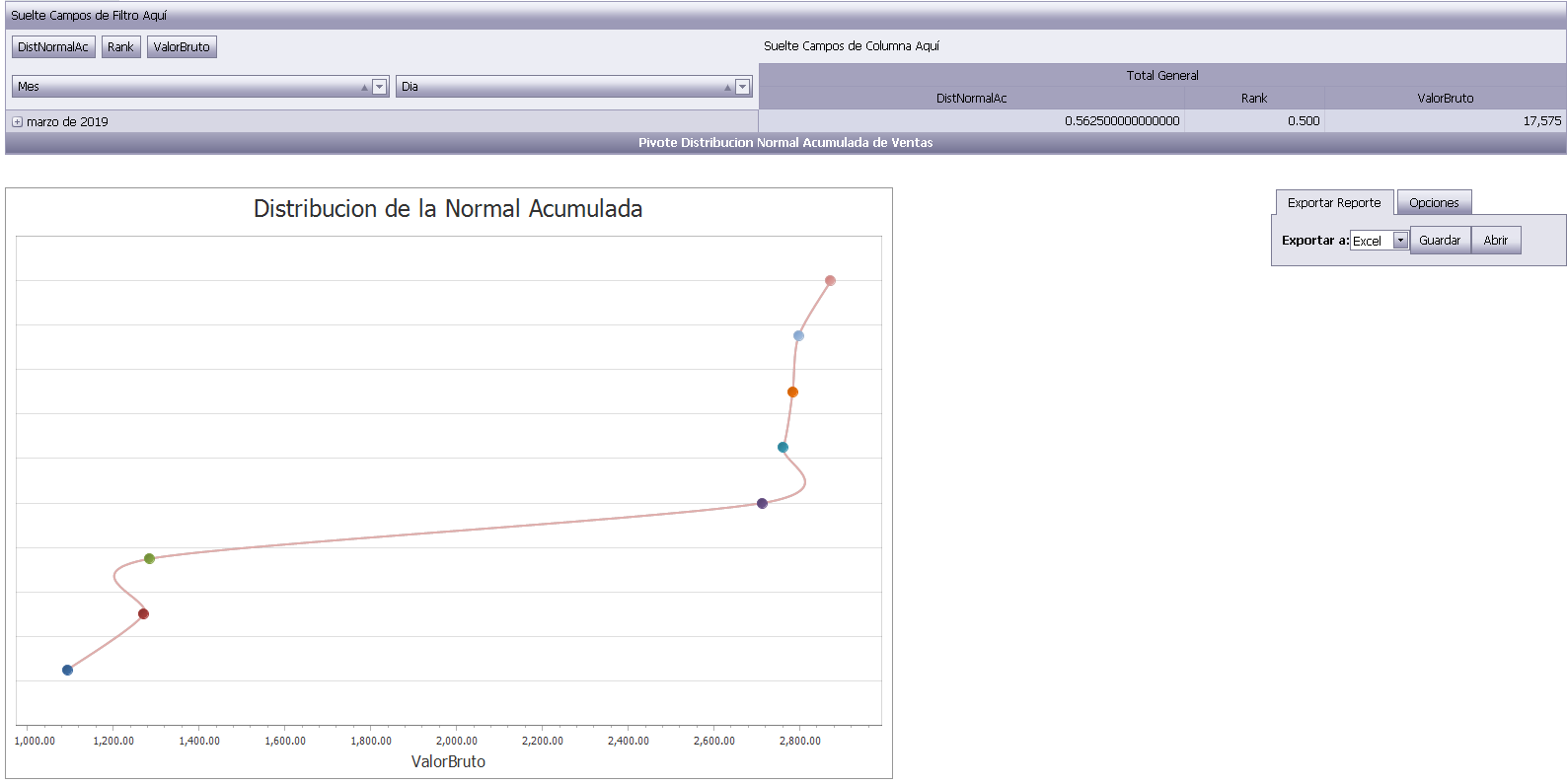
Il s'agit d'un logiciel gratuit et non encombré publié dans le domaine public - voir le fichier de licence pour plus de détails.
Fabriqué avec ❤️ par Javier Cañon.