Distribuição normal do SQL Server, Gauss ou Bell Curve
A distribuição normal é a distribuição de probabilidade mais importante nas estatísticas porque se encaixa em muitos fenômenos naturais. Por exemplo, alturas, pressão arterial, erro de medição e pontuações de QI seguem a distribuição normal. Também é conhecido como distribuição gaussiana e curva de sino.
A distribuição normal é uma função de probabilidade que descreve como os valores de uma variável são distribuídos. É uma distribuição simétrica em que a maioria das observações se agrupa ao redor do pico central e as probabilidades de valores mais longe da média da diminuição igualmente em ambas as direções. Os valores extremos nas duas caudas da distribuição são igualmente improváveis.
Nesta postagem do blog, você aprenderá a usar a distribuição normal, seus parâmetros e como calcular as escores Z para padronizar seus dados e encontrar probabilidades. Exemplo de dados normalmente distribuídos: alturas
Os dados de altura são normalmente distribuídos. A distribuição neste exemplo se encaixa em dados reais que eu colecionei de meninas de 14 anos durante um estudo.
Distribuição normal de alturas.
Como você pode ver, a distribuição de alturas segue o padrão típico para todas as distribuições normais. A maioria das meninas está próxima da média (1,512 metros). Pequenas diferenças entre a altura de um indivíduo e a média ocorrem com mais frequência do que os desvios substanciais da média. O desvio padrão é de 0,0741m, o que indica a distância típica que as meninas individuais tendem a cair da altura média.
A distribuição é simétrica. O número de meninas mais curtas que a média é igual ao número de meninas mais altas que a média. Em ambas as caudas da distribuição, meninas extremamente curtas ocorrem tão frequentemente quanto garotas extremamente altas. Parâmetros da distribuição normal
Como em qualquer distribuição de probabilidade, os parâmetros para a distribuição normal definem completamente sua forma e probabilidades. A distribuição normal possui dois parâmetros, a média e o desvio padrão. A distribuição normal não tem apenas uma forma. Em vez disso, a forma muda com base nos valores dos parâmetros, conforme mostrado nos gráficos abaixo. Significar
A média é a tendência central da distribuição. Ele define a localização do pico para distribuições normais. A maioria dos valores se agrupa em torno da média. Em um gráfico, alterar a média muda a curva inteira para a esquerda ou direita no eixo x.
Gráfico que exibe distribuições normais com meios diferentes. Desvio padrão
O desvio padrão é uma medida de variabilidade. Define a largura da distribuição normal. O desvio padrão determina a distância da média que os valores tendem a cair. Representa a distância típica entre as observações e a média.
Em um gráfico, alterar o desvio padrão aperta ou espalha a largura da distribuição ao longo do eixo x. Desvios padrão maiores produzem distribuições que são mais espalhadas.
Gráfico que exibe distribuições normais com diferentes desvios padrão.
Quando você tem distribuições estreitas, as probabilidades são mais altas de que os valores não caem longe da média. À medida que você aumenta a disseminação da distribuição, a probabilidade de as observações estarão mais longe da média também aumenta. Parâmetros populacionais versus estimativas de amostra
A média e o desvio padrão são valores de parâmetros que se aplicam a populações inteiras. Para a distribuição normal, os estatísticos significam os parâmetros usando o símbolo grego μ (MU) para a média da população e σ (sigma) para o desvio padrão da população.
Infelizmente, os parâmetros populacionais geralmente são desconhecidos porque geralmente é impossível medir uma população inteira. No entanto, você pode usar amostras aleatórias para calcular estimativas desses parâmetros. Os estatísticos representam estimativas de amostra desses parâmetros usando x̅ para a média da amostra e S para o desvio padrão da amostra.
Postagens relacionadas: medidas de tendência central e medidas de variabilidade comuns propriedades para todas as formas da distribuição normal
Apesar das diferentes formas, todas as formas da distribuição normal têm as seguintes propriedades características.
They’re all symmetric. The normal distribution cannot model skewed distributions.
The mean, median, and mode are all equal.
Half of the population is less than the mean and half is greater than the mean.
The Empirical Rule allows you to determine the proportion of values that fall within certain distances from the mean. More on this below!
Embora a distribuição normal seja essencial nas estatísticas, é apenas uma das muitas distribuições de probabilidade e não se encaixa em todas as populações. Para saber como determinar se a distribuição normal fornece o melhor ajuste aos dados da amostra, leia minhas postagens sobre como identificar a distribuição de seus dados e avaliar a normalidade: histogramas versus gráficos de probabilidade normal. A regra empírica para a distribuição normal
Quando você normalmente distribui dados, o desvio padrão se torna particularmente valioso. Você pode usá -lo para determinar a proporção dos valores que se enquadram em um número especificado de desvios padrão da média. Por exemplo, em uma distribuição normal, 68% das observações se enquadram +/- 1 desvio padrão da média. Essa propriedade faz parte da regra empírica, que descreve a porcentagem dos dados que se enquadram em números específicos de desvios padrão da média das curvas em forma de sino. Média +/- Desvios padrão porcentagem de dados continha 1 68% 2 95% 3 99,7%
Vejamos um exemplo de entrega de pizza. Suponha que um restaurante de pizza tenha um período de entrega média de 30 minutos e um desvio padrão de 5 minutos. Usando a regra empírica, podemos determinar que 68% dos prazos de entrega estão entre 25-35 minutos (30 +/- 5), 95% estão entre 20-40 minutos (30 +/- 2 5) e 99,7% estão entre 15-45 minutos (30 +/- 3 5). O gráfico abaixo ilustra essa propriedade graficamente.
Gráfico que exibe uma distribuição normal com áreas divididas por desvios padrão. Distribuição normal padrão e pontuações padrão
Como vimos acima, a distribuição normal tem muitas formas diferentes, dependendo dos valores dos parâmetros. No entanto, a distribuição normal padrão é um caso especial da distribuição normal, onde a média é zero e o desvio padrão é 1. Essa distribuição também é conhecida como distribuição z.
Um valor na distribuição normal padrão é conhecido como pontuação padrão ou uma escore z. Uma pontuação padrão representa o número de desvios padrão acima ou abaixo do meio que uma observação específica cai. Por exemplo, uma pontuação padrão de 1,5 indica que a observação é de 1,5 desvios padrão acima da média. Por outro lado, uma pontuação negativa representa um valor abaixo da média. A média tem um escore z de 0.
Gráfico que exibe uma distribuição normal padrão.
Suponha que você pesa uma maçã e pesa 110 gramas. Não há como dizer apenas pelo peso como esta maçã se compara a outras maçãs. No entanto, como você verá, depois de calcular o seu escore z, você sabe onde ele cai em relação a outras maçãs. Padronização: como calcular as escores Z
As pontuações padrão são uma ótima maneira de entender onde uma observação específica cai em relação a toda a distribuição. Eles também permitem que você faça observações extraídas de populações normalmente distribuídas que possuem meios diferentes e desvios padrão e os coloque em uma escala padrão. Esta escala padrão permite comparar observações que, de outra forma, seriam difíceis.
Esse processo é chamado de padronização e permite comparar observações e calcular probabilidades em diferentes populações. Em outras palavras, permite comparar maçãs com laranjas. Não é estatística ótima!
Para padronizar seus dados, você precisa converter as medições brutas em escores z.
Para calcular a pontuação padrão para uma observação, faça a medição bruta, subtraia a média e divida pelo desvio padrão. Matematicamente, a fórmula para esse processo é o seguinte:
Z = { displayStyle frac { text {x} - mu} { sigma}}
X representa o valor bruto da medição de juros. Mu e Sigma representam os parâmetros da população da qual a observação foi retirada.
Depois de padronizar seus dados, você pode colocá -los dentro da distribuição normal padrão. Dessa maneira, a padronização permite comparar diferentes tipos de observações com base em onde cada observação se enquadra em sua própria distribuição. Exemplo de uso de pontuações padrão para fazer maçãs para laranjas comparação
Suponha que literalmente queremos comparar maçãs com laranjas. Especificamente, vamos comparar seus pesos. Imagine que temos uma maçã que pesa 110 gramas e uma laranja que pesa 100 gramas.
Se compararmos os valores brutos, é fácil ver que a maçã pesa mais que a laranja. No entanto, vamos comparar suas pontuações padrão. Para fazer isso, precisaremos conhecer as propriedades das distribuições de peso para maçãs e laranjas. Suponha que os pesos de maçãs e laranjas sigam uma distribuição normal com os seguintes valores de parâmetros: maçãs laranjas significam grama de peso 100 140 Desvio padrão 15 25
Agora vamos calcular os escores Z:
Apple = 110-100/15 = 0.667
Orange = 100-140/25 = -1.6
O escore Z para a Apple (0,667) é positivo, o que significa que nossa Apple pesa mais do que a maçã média. Não é um valor extremo por qualquer meio, mas está acima da média para maçãs. Por outro lado, a laranja possui escore z razoavelmente negativo (-1,6). Está bem abaixo do peso médio para laranjas. Coloquei esses valores z na distribuição normal padrão abaixo.
Gráfico de uma distribuição normal padrão que compara maçãs a laranjas usando uma pontuação z.
Enquanto nossa maçã pesa mais que a nossa laranja, estamos comparando uma maçã um pouco mais pesada que a média com uma laranja insignificante! Usando escores z, aprendemos como cada fruta se encaixa em sua própria distribuição e como elas se comparam. Encontrar áreas sob a curva de uma distribuição normal
A distribuição normal é uma distribuição de probabilidade. Como em qualquer distribuição de probabilidade, a proporção da área que se enquadra na curva entre dois pontos em um gráfico de distribuição de probabilidade indica a probabilidade de que um valor cairá dentro desse intervalo. Para saber mais sobre essa propriedade, leia meu post sobre a compreensão das distribuições de probabilidade.
Normalmente, eu uso software estatístico para encontrar áreas sob a curva. No entanto, quando você está trabalhando com a distribuição normal e converter valores em pontuações padrão, pode calcular áreas procurando escores Z em uma tabela de distribuição normal padrão.
Como há um número infinito de diferentes distribuições normais, os editores não podem imprimir uma tabela para cada distribuição. No entanto, você pode transformar os valores de qualquer distribuição normal em escores z e, em seguida, usar uma tabela de pontuações padrão para calcular probabilidades. Usando uma tabela de escores Z
Vamos pegar o escore Z para a nossa Apple (0,667) e usá-lo para determinar seu percentil de peso. Um percentil é a proporção de uma população que cai abaixo de um valor específico. Consequentemente, para determinar o percentil, precisamos encontrar a área que corresponda à faixa de escores z que são inferiores a 0,667. Na parte da tabela abaixo, o escore Z mais próximo do nosso é de 0,65, que usaremos.
A fotografia mostra uma parte de uma tabela de pontuações padrão (escores z).
O truque dessas tabelas é usar os valores em conjunto com as propriedades da distribuição normal para calcular a probabilidade de que você precisa. O valor da tabela indica que a área da curva entre -0,65 e +0,65 é de 48,43%. No entanto, não é isso que queremos saber. Queremos a área menor que um escore Z de 0,65.
Sabemos que as duas metades da distribuição normal são imagens espelhadas uma da outra. Portanto, se a área para o intervalo de -0,65 e +0,65 for 48,43%, o intervalo de 0 a +0,65 deve ser metade disso: 48,43/2 = 24,215%. Além disso, sabemos que a área para todas as pontuações inferiores a zero é metade (50%) da distribuição.
Portanto, a área para todas as pontuações de até 0,65 = 50% + 24,215% = 74,215%
Nossa maçã está aproximadamente no 74º percentil.
Abaixo está um gráfico de distribuição de probabilidade produzido por software estatístico que mostra o mesmo percentil, juntamente com uma representação gráfica da área correspondente sob a curva. O valor é um pouco diferente porque usamos um escore z de 0,65 da tabela, enquanto o software usa o valor mais preciso de 0,667.
Um gráfico de distribuição de probabilidade que exibe graficamente um percentil usando uma pontuação z. Outras razões pelas quais a distribuição normal é importante
Além de todas as opções acima, existem várias outras razões pelas quais a distribuição normal é crucial nas estatísticas.
Some statistical hypothesis tests assume that the data follow a normal distribution. However, as I explain in my post about parametric and nonparametric tests, there’s more to it than only whether the data are normally distributed.
Linear and nonlinear regression both assume that the residuals follow a normal distribution. Learn more in my post about assessing residual plots.
The central limit theorem states that as the sample size increases, the sampling distribution of the mean follows a normal distribution even when the underlying distribution of the original variable is non-normal.
Isso foi um pouco sobre a distribuição normal! Felizmente, você pode entender que é crucial por causa das muitas maneiras pelas quais os analistas o usam.
Fonte: https://statisticsbyjim.com/basics/normal-distribution/

Probabilidade cumulativa de uma distribuição normal com valor esperado 0 e desvio padrão 1: 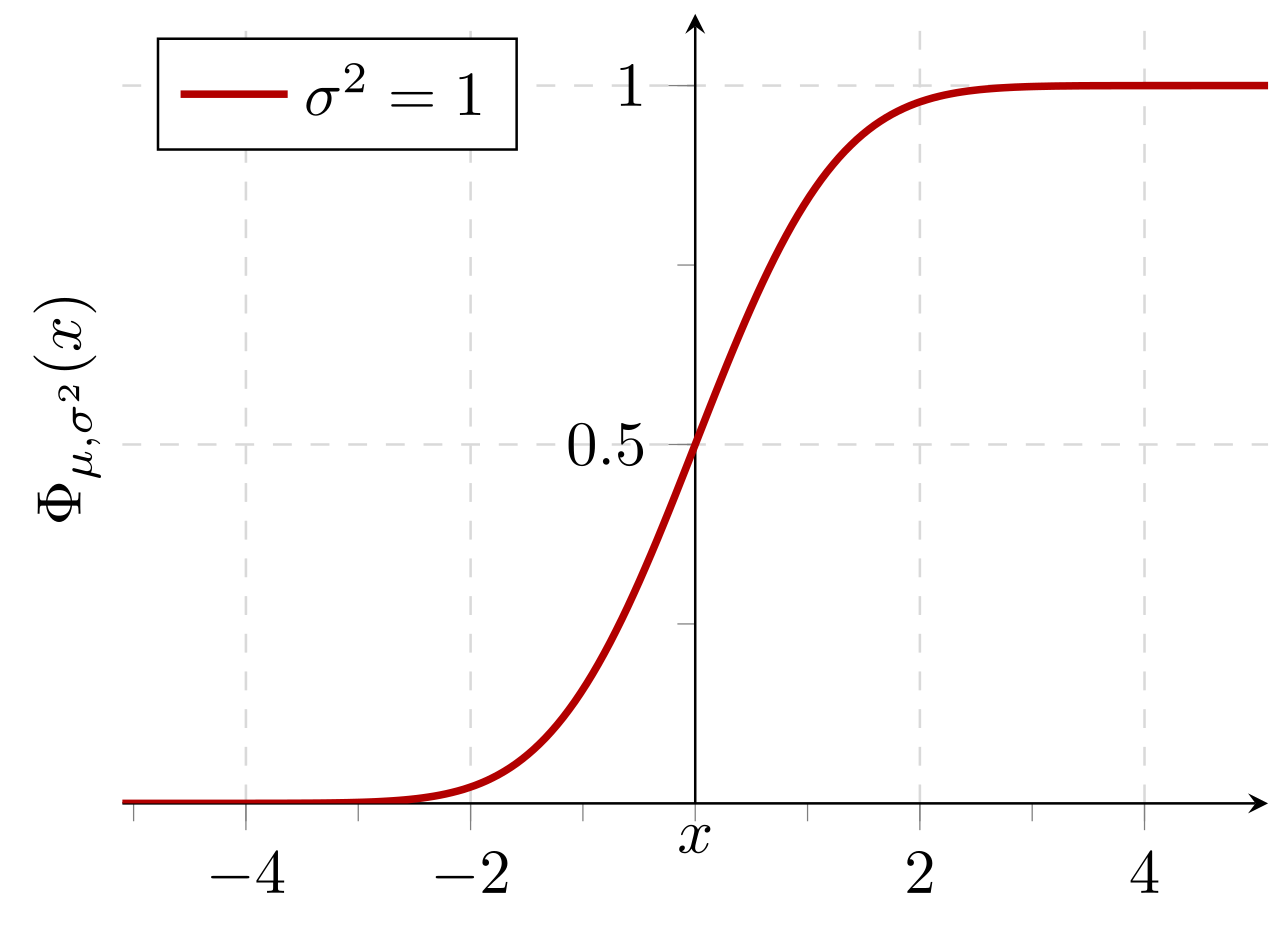
Este é um software gratuito e não onerado lançado no domínio público - consulte o arquivo de licença para obter detalhes.
Feito com ❤️ por Javier Cañon.