SQL Server 정규 분포, 가우스 또는 벨 곡선
정규 분포는 통계에서 가장 중요한 확률 분포가 많은 자연 현상에 적합하기 때문입니다. 예를 들어, 높이, 혈압, 측정 오류 및 IQ 점수는 정규 분포를 따릅니다. 가우스 분포와 벨 곡선이라고도합니다.
정규 분포는 변수 값이 분포되는 방법을 설명하는 확률 기능입니다. 그것은 대부분의 관측치가 중앙 피크 주변의 클러스터와 평균 테이퍼 꺼짐으로부터 양방향으로 동일하게 값을 멀리 떨어진 값에 대한 확률이 대칭 분포입니다. 분포의 두 꼬리의 극단적 값은 비슷하지 않습니다.
이 블로그 게시물에서는 정규 분포, 매개 변수를 사용하는 방법 및 데이터를 표준화하여 데이터를 표준화하고 확률을 찾는 방법을 배웁니다. 정규 분포 데이터의 예 : 높이
높이 데이터는 일반적으로 분포됩니다. 이 예제의 분포는 연구 중에 14 세 소녀로부터 수집 한 실제 데이터에 적합합니다.
높이의 정규 분포.
보시다시피, 높이 분포는 모든 정규 분포에 대한 일반적인 패턴을 따릅니다. 대부분의 소녀들은 평균 (1.512 미터)에 가깝습니다. 개인의 높이와 평균의 작은 차이는 평균과의 상당한 편차보다 더 자주 발생합니다. 표준 편차는 0.0741m이며, 이는 개별 소녀들이 평균 높이에서 떨어지는 경향이있는 전형적인 거리를 나타냅니다.
분포는 대칭입니다. 평균보다 짧은 소녀의 수는 평균보다 키가 큰 소녀의 수와 같습니다. 분포의 두 꼬리에서, 매우 짧은 소녀는 매우 키가 큰 소녀들처럼 드물게 발생합니다. 정규 분포의 매개 변수
확률 분포와 마찬가지로, 정규 분포의 매개 변수는 그 모양과 확률을 완전히 정의합니다. 정규 분포에는 평균 및 표준 편차의 두 매개 변수가 있습니다. 정규 분포에는 단 하나의 형태가 없습니다. 대신, 아래 그래프에 표시된대로 매개 변수 값에 따라 모양이 변경됩니다. 평균
평균은 분포의 중심 경향입니다. 정상 분포에 대한 피크의 위치를 정의합니다. 대부분의 값은 평균 주위에 클러스터됩니다. 그래프에서 평균 변경은 X 축에서 왼쪽 또는 오른쪽으로 전체 곡선을 이동시킵니다.
다른 수단으로 일반 분포를 표시하는 그래프. 표준 편차
표준 편차는 변동성의 척도입니다. 정규 분포의 너비를 정의합니다. 표준 편차는 값이 평균에서 떨어지는 경향이 얼마나 떨어지는지를 결정합니다. 관측치와 평균 사이의 일반적인 거리를 나타냅니다.
그래프에서 표준 편차를 변경하면 x 축을 따라 분포의 너비가 조여 지거나 퍼집니다. 더 큰 표준 편차는 더 확산되는 분포를 생성합니다.
다른 표준 편차로 일반 분포를 표시하는 그래프.
분포가 좁아지면 값이 평균에서 멀지 않을 것이라는 확률이 높습니다. 분포의 확산을 증가 시키면 관찰이 평균으로부터 멀어 질 가능성도 증가 할 것입니다. 모집단 매개 변수 대 샘플 추정치
평균 및 표준 편차는 전체 모집단에 적용되는 매개 변수 값입니다. 정규 분포의 경우 통계 학자는 모집단 평균에 그리스 기호 μ (MU)를 사용하고 모집단 표준 편차에 대해 σ (Sigma)를 사용하여 매개 변수를 나타냅니다.
불행히도, 인구 매개 변수는 일반적으로 전체 인구를 측정하는 것이 불가능하기 때문에 알 수 없습니다. 그러나 임의의 샘플을 사용하여 이러한 매개 변수의 추정치를 계산할 수 있습니다. 통계 학자는 샘플 평균에 대해 x̅ 및 샘플 표준 편차에 대한 s를 사용하여 이러한 매개 변수의 샘플 추정치를 나타냅니다.
관련 게시물 : 정규 분포의 모든 형태에 대한 중심 경향 및 변동성 공통 특성 측정
다른 모양에도 불구하고, 모든 형태의 정규 분포는 다음 특성 특성을 갖는다.
They’re all symmetric. The normal distribution cannot model skewed distributions.
The mean, median, and mode are all equal.
Half of the population is less than the mean and half is greater than the mean.
The Empirical Rule allows you to determine the proportion of values that fall within certain distances from the mean. More on this below!
정규 분포는 통계에 필수적이지만 많은 확률 분포 중 하나 일 뿐이며 모든 인구에 적합하지는 않습니다. 정규 분포가 샘플 데이터에 가장 적합한 지 여부를 결정하는 방법을 배우려면 데이터 분포를 식별하고 정규성 평가 방법 : 히스토그램 대 정상 확률 플롯을 평가하는 방법에 대한 게시물을 읽으십시오. 정규 분포에 대한 경험적 규칙
일반적으로 분산 된 데이터가 있으면 표준 편차가 특히 가치가 있습니다. 이를 사용하여 평균에서 지정된 표준 편차 수에 해당하는 값의 비율을 결정할 수 있습니다. 예를 들어, 정규 분포에서 관찰의 68%가 평균에서 +/- 1 표준 편차 내에 있습니다. 이 속성은 경험적 규칙의 일부이며, 벨 모양의 곡선의 평균에서 특정 표준 편차에 해당하는 데이터의 백분율을 설명합니다. 평균 +/- 표준 편차 데이터의 백분율 1 68% 2 95% 3 99.7%
피자 배달 예를 살펴 보겠습니다. 피자 식당의 평균 배달 시간은 30 분이고 표준 편차가 5 분이라고 가정하십시오. 경험적 규칙을 사용하여 배달 시간의 68%가 25-35 분 (30 +/- 5), 95%는 20-40 분 (30 +/- 2 5)이며 99.7%는 15-45 분 (30 +/- 3 5)이라고 판단 할 수 있습니다. 아래 차트는이 속성을 그래픽으로 보여줍니다.
영역을 표준 편차로 나눈 정규 분포를 표시하는 그래프. 표준 정규 분포 및 표준 점수
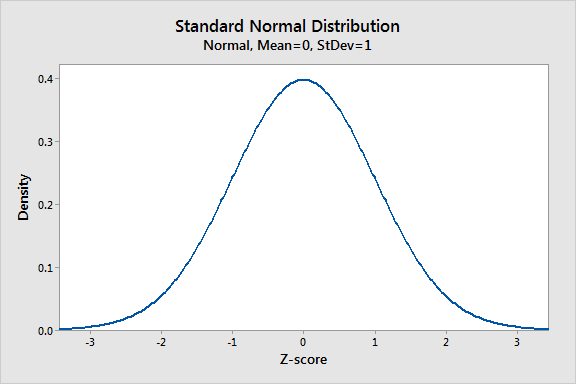
위에서 볼 수 있듯이 정규 분포에는 매개 변수 값에 따라 여러 가지 모양이 있습니다. 그러나 표준 정규 분포는 평균이 0이고 표준 편차가 1 인 정규 분포의 특수한 경우입니다.이 분포는 Z- 분포라고도합니다.
표준 정규 분포의 값은 표준 점수 또는 Z- 점수라고합니다. 표준 점수는 특정 관측치가 떨어지는 평균 위 또는 아래의 표준 편차 수를 나타냅니다. 예를 들어, 표준 점수 1.5는 관찰이 평균보다 1.5 표준 편차임을 나타냅니다. 반면, 음의 점수는 평균보다 낮은 값을 나타냅니다. 평균의 z- 점수는 0입니다.
표준 정규 분포를 표시하는 그래프.
사과의 무게와 무게는 110 그램이라고 가정합니다. 무게 만으로이 사과가 다른 사과와 어떻게 비교되는지 알 수있는 방법은 없습니다. 그러나 알 수 있듯이 Z- 점수를 계산 한 후 다른 사과에 비해 어디에 있는지 알 수 있습니다. 표준화 : z- 점수를 계산하는 방법
표준 점수는 전체 분포에 비해 특정 관찰이 어디에 있는지 이해하는 좋은 방법입니다. 또한 평균과 표준 편차가 다른 정규 분포 인구에서 도출 된 관찰을 통해 표준 척도로 배치 할 수 있습니다. 이 표준 척도를 사용하면 어려운 관찰을 비교할 수 있습니다.
이 프로세스를 표준화라고하며 관측치를 비교하고 다른 인구의 확률을 계산할 수 있습니다. 다시 말해, 사과를 오렌지와 비교할 수 있습니다. 통계가 좋지 않습니다!
데이터를 표준화하려면 원시 측정 값을 z- 스코어로 변환해야합니다.
관찰의 표준 점수를 계산하려면 원시 측정을 수행하고 평균을 빼고 표준 편차로 나눕니다. 수학적으로 해당 과정의 공식은 다음과 같습니다.
z = { displaystyle frac { text {x} - mu} { sigma}}
X는 관심 측정의 원시 값을 나타냅니다. MU와 Sigma는 관찰이 그려진 모집단의 매개 변수를 나타냅니다.
데이터를 표준화 한 후에는 표준 정규 분포 내에 데이터를 배치 할 수 있습니다. 이러한 방식으로 표준화를 통해 각 관측치가 자체 분포 내에있는 위치에 따라 다양한 유형의 관찰을 비교할 수 있습니다. 표준 점수를 사용하여 사과 대 오렌지 비교를 만드는 예
우리가 말 그대로 사과를 오렌지와 비교하고 싶다고 가정합니다. 구체적으로, 그들의 무게를 비교해 봅시다. 무게가 110 그램의 사과와 무게가 100 그램의 오렌지가 있다고 상상해보십시오.
원시 값을 비교하면 사과의 무게가 오렌지보다 더 많다는 것을 쉽게 알 수 있습니다. 그러나 표준 점수를 비교해 봅시다. 이를 위해서는 사과와 오렌지의 중량 분포의 특성을 알아야합니다. 사과와 오렌지의 무게가 다음 매개 변수 값으로 정규 분포를 따른다고 가정합니다. 사과 오렌지 평균 무게 그램 100 140 표준 편차 15 25
이제 z- 스코어를 계산할 것입니다.
Apple = 110-100/15 = 0.667
Orange = 100-140/25 = -1.6
Apple의 Z- 점수 (0.667)는 양수이므로 사과의 무게는 평균 사과보다 높습니다. 그것은 어떤 식 으로든 극단적 인 가치는 아니지만 사과의 평균 이상입니다. 반면에 오렌지는 상당히 음수 Z- 점수 (-1.6)를 가지고 있습니다. 오렌지의 평균 무게보다 훨씬 낮습니다. 이 z- 값을 아래 표준 정규 분포에 배치했습니다.
z- 점수를 사용하여 사과를 오렌지와 비교하는 표준 정규 분포의 그래프.
우리의 사과 무게는 우리의 오렌지보다 더 높지만, 우리는 평균 사과보다 다소 무거운 것을 완전히 삐걱 거리는 오렌지와 비교하고 있습니다! Z- 스코어를 사용하여 각 과일이 자체 분포 내에 어떻게 적합한 지, 서로 비교하는 방법을 배웠습니다. 정규 분포 곡선 아래 영역을 찾습니다
정규 분포는 확률 분포입니다. 확률 분포와 마찬가지로 확률 분포 플롯에서 두 지점 사이의 곡선 아래에있는 영역의 비율은 값이 해당 간격에 속할 확률을 나타냅니다. 이 속성에 대한 자세한 내용은 확률 분포 이해에 대한 내 게시물을 읽으십시오.
일반적으로 통계 소프트웨어를 사용하여 곡선 아래의 영역을 찾습니다. 그러나 정규 분포를 사용하고 값을 표준 점수로 변환 할 때 표준 정규 분포 테이블에서 z- 점수를 찾아 영역을 계산할 수 있습니다.
무한한 수의 정상 분포가 있기 때문에 게시자는 각 배포에 대한 테이블을 인쇄 할 수 없습니다. 그러나 값을 정규 분포에서 Z- 스코어로 변환 한 다음 표준 점수 테이블을 사용하여 확률을 계산할 수 있습니다. Z- 스코어 테이블 사용
Apple (0.667)의 Z- 점수를 받아 중량 백분위 수를 결정하는 데 사용합시다. 백분위 수는 특정 값보다 낮은 인구의 비율입니다. 결과적으로 백분위 수를 결정하기 위해서는 0.667 미만의 Z- 점수 범위에 해당하는 영역을 찾아야합니다. 아래 표의 부분에서 가장 가까운 z- 점수는 0.65이며, 우리는 사용할 것입니다.
사진은 표준 점수 (Z- 스코어)의 일부를 보여줍니다.
이 테이블의 트릭은 정규 분포의 특성과 함께 값을 사용하여 필요한 확률을 계산하는 것입니다. 테이블 값은 -0.65와 +0.65 사이의 곡선 영역이 48.43%임을 나타냅니다. 그러나 그것은 우리가 알고 싶은 것이 아닙니다. 우리는 0.65의 z- 점수 미만의 영역을 원합니다.
우리는 정규 분포의 두 절반이 서로의 거울 이미지라는 것을 알고 있습니다. 따라서 -0.65 및 +0.65 간격의 영역이 48.43%인 경우 0에서 +0.65 사이의 범위는 48.43/2 = 24.215%의 절반이어야합니다. 또한 모든 점수에 대한 영역은 0보다 작은 영역이 분포의 절반 (50%)임을 알고 있습니다.
따라서 모든 점수의 영역은 최대 0.65 = 50% + 24.215% = 74.215%입니다.
우리의 사과는 대략 74 번째 백분위 수입니다.
아래는 통계 소프트웨어에 의해 생성 된 확률 분포 플롯으로, 곡선 아래의 해당 영역의 그래픽 표현과 함께 동일한 백분위 수를 보여줍니다. 테이블에서 0.65의 z- 점수를 사용하고 소프트웨어는 0.667의 더 정확한 값을 사용하기 때문에 값은 약간 다릅니다.
z- 점수를 사용하여 백분위 수를 그래픽으로 표시하는 확률 분포 플롯. 정규 분포가 중요한 다른 이유
위의 모든 것 외에도 정규 분포가 통계에 중요한 이유가 몇 가지 있습니다.
Some statistical hypothesis tests assume that the data follow a normal distribution. However, as I explain in my post about parametric and nonparametric tests, there’s more to it than only whether the data are normally distributed.
Linear and nonlinear regression both assume that the residuals follow a normal distribution. Learn more in my post about assessing residual plots.
The central limit theorem states that as the sample size increases, the sampling distribution of the mean follows a normal distribution even when the underlying distribution of the original variable is non-normal.
그것은 정규 분포에 대해 꽤 조금이었다! 바라건대, 당신은 분석가들이 그것을 사용하는 많은 방법 때문에 그것이 중요하다는 것을 이해할 수 있기를 바랍니다.
출처 : https://statisticsbyjim.com/basics/normal-distribution/

예상 값 0 및 표준 편차를 갖는 정규 분포의 누적 확률 : 1 : 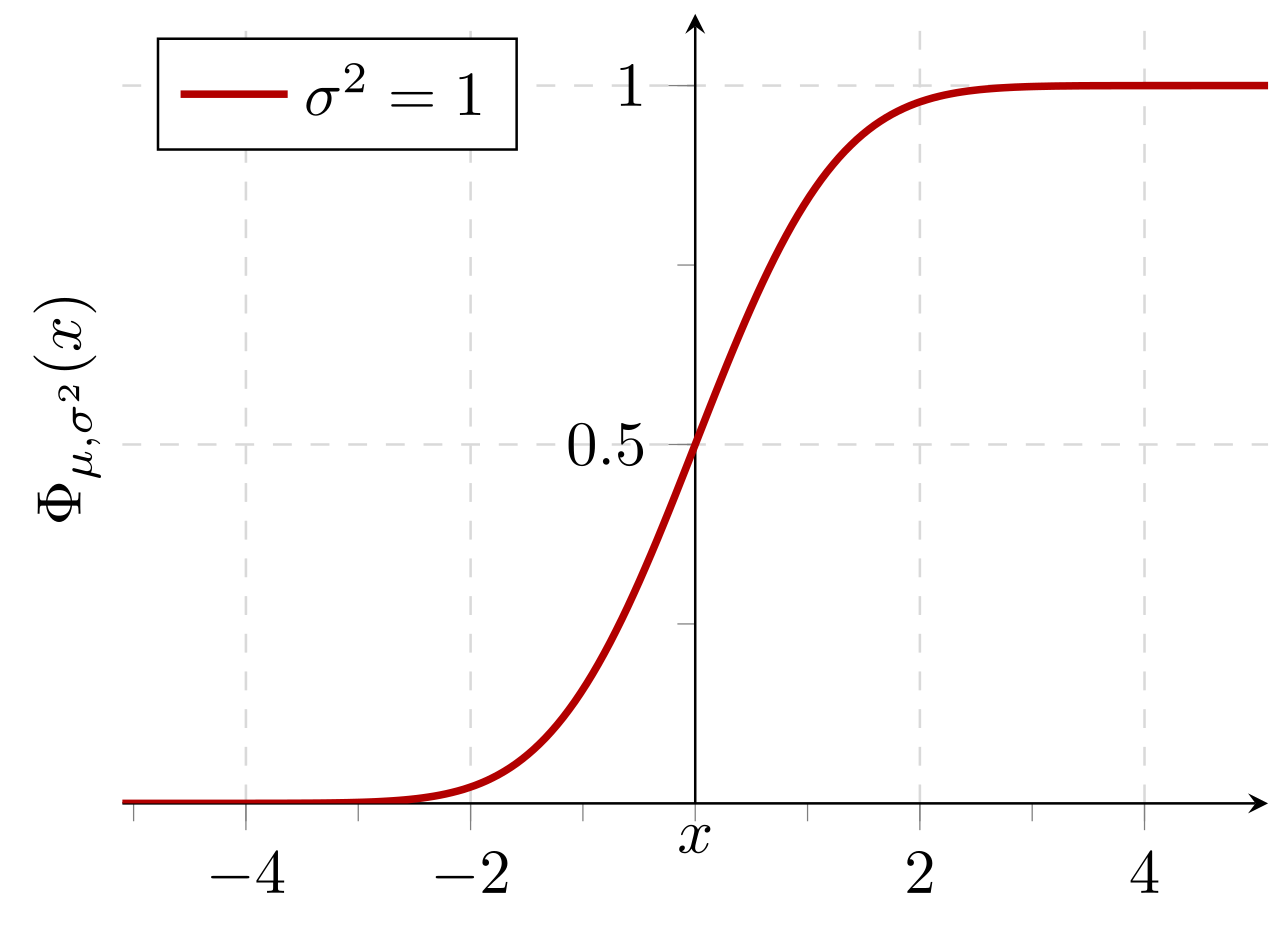
이것은 무료 및 방해받지 않은 소프트웨어가 공개 도메인에 공개됩니다. 자세한 내용은 라이센스 파일을 참조하십시오.
Javier Cañon의 ❤️으로 제작되었습니다.