SQLサーバーの正規分布、ガウスまたはベル曲線
正規分布は、多くの自然現象に適合するため、統計における最も重要な確率分布です。たとえば、高さ、血圧、測定誤差、IQスコアは正規分布に続きます。また、ガウス分布とベル曲線としても知られています。
正規分布は、変数の値がどのように分布するかを記述する確率関数です。これは、ほとんどの観測値が中央のピークの周りにクラスター化され、平均テーパーからさらに離れた値の確率が両方向に等しくオフになる対称分布です。分布の両方の尾の極値は同様にありそうもない。
このブログ投稿では、正規分布、そのパラメーター、およびZスコアを計算してデータを標準化して確率を見つける方法を学びます。通常分布したデータの例:高さ
高さデータは通常分布しています。この例の分布は、研究中に14歳の少女から収集した実際のデータに適合しています。
高さの正規分布。
ご覧のとおり、高さの分布は、すべての通常の分布の典型的なパターンに従います。ほとんどの女の子は平均に近い(1.512メートル)。個人の身長と平均の間の小さな違いは、平均からの実質的な偏差よりも頻繁に発生します。標準偏差は0.0741mであり、これは個々の女の子が平均高さから落ちる傾向がある典型的な距離を示しています。
分布は対称です。平均よりも短い女の子の数は、平均よりも高い女の子の数に等しくなります。分布の両方の尾で、非常に短い女の子が非常に背の高い女の子と同じくらいまれに起こります。正規分布のパラメーター
確率分布と同様に、正規分布のパラメーターはその形状と確率を完全に定義します。正規分布には、平均偏差と標準偏差という2つのパラメーターがあります。正規分布には、1つのフォームだけがありません。代わりに、以下のグラフに示すように、形状はパラメーター値に基づいて変化します。平均
平均は、分布の中心的な傾向です。通常の分布のピークの位置を定義します。ほとんどの値は平均の周りにクラスター化されます。グラフでは、平均を変更すると、曲線全体がX軸の左または右にシフトします。
異なる手段で通常の分布を表示するグラフ。標準偏差
標準偏差は変動の尺度です。正規分布の幅を定義します。標準偏差は、値が下落する傾向がある平均からどれだけ離れているかを決定します。観測と平均の間の典型的な距離を表します。
グラフでは、標準偏差を変更すると、X軸に沿って分布の幅を締めたり広げたりします。より大きな標準偏差は、より広がる分布を生成します。
異なる標準偏差で通常の分布を表示するグラフ。
狭い分布がある場合、確率は平均から遠く離れないようにする確率が高くなります。分布の拡大を増やすと、観測が平均からさらに離れる可能性も増加します。人口パラメーターとサンプルの推定値
平均および標準偏差は、集団全体に適用されるパラメーター値です。正規分布の場合、統計学者は、ギリシャのシンボルμ(MU)を母集団平均に、母集団標準偏差にσ(Sigma)を使用してパラメーターを意味します。
残念ながら、人口全体を測定することは一般に不可能であるため、人口パラメーターは通常不明です。ただし、ランダムサンプルを使用して、これらのパラメーターの推定値を計算できます。統計学者は、サンプル平均に対してx̅を使用して、サンプル標準偏差にSを使用して、これらのパラメーターのサンプル推定値を表します。
関連する投稿:中央の傾向の測定と変動性の測定正規分布のあらゆる形態の共通特性
異なる形状にもかかわらず、すべての形式の正規分布には、次の特性特性があります。
They’re all symmetric. The normal distribution cannot model skewed distributions.
The mean, median, and mode are all equal.
Half of the population is less than the mean and half is greater than the mean.
The Empirical Rule allows you to determine the proportion of values that fall within certain distances from the mean. More on this below!
正規分布は統計では不可欠ですが、多くの確率分布の1つにすぎず、すべての集団に適合しません。正規分布がサンプルデータに最適な適合を提供するかどうかを判断する方法を学ぶには、データの分布を識別し、正規性を評価する方法についての投稿を読んでください:ヒストグラムと通常の確率プロット。正規分布の経験的ルール
通常、データを分散している場合、標準偏差は特に価値があります。それを使用して、平均から指定された数の標準偏差内に該当する値の割合を決定できます。たとえば、正規分布では、観測の68%が平均から+/- 1標準偏差内に該当します。このプロパティは経験的ルールの一部であり、ベル型曲線の平均からの特定の数の標準偏差に該当するデータの割合を説明しています。平均+/-標準偏差データの割合を含む1 68%2 95%3 99.7%
ピザ配達の例を見てみましょう。ピザレストランの配送時間は30分、標準偏差が5分であると仮定します。経験的規則を使用すると、出産時間の68%が25〜35分(30 +/- 5)、95%が20〜40分(30 +/- 2 5)、99.7%が15〜45分(30 +/- 3 5)の間であると判断できます。以下のチャートは、このプロパティをグラフィカルに示しています。
領域を標準偏差で割った正規分布を表示するグラフ。標準の正規分布と標準スコア
上で見たように、正規分布はパラメーター値に応じてさまざまな形状を持っています。ただし、標準的な正規分布は、平均がゼロで標準偏差が1である正規分布の特殊なケースです。この分布はZ分布としても知られています。
標準正規分布の値は、標準スコアまたはZスコアとして知られています。標準スコアは、特定の観察が低下する平均を上または下回る標準偏差の数を表します。たとえば、1.5の標準スコアは、観測が平均を上回る1.5標準偏差であることを示しています。一方、負のスコアは平均以下の値を表します。平均のZスコアは0です。
標準的な正規分布を表示するグラフ。
リンゴの重さを量ると、体重が110グラムであるとします。このリンゴが他のリンゴとどのように比較されるかだけで、体重だけから言う方法はありません。ただし、ご覧のとおり、Zスコアを計算した後、他のリンゴと比較してどこに落ちるかがわかります。標準化:Zスコアの計算方法
標準スコアは、分布全体に比べて特定の観察がどこにあるかを理解するための優れた方法です。また、さまざまな手段と標準偏差を持つ通常分布の集団から引き出された観察結果を取り、標準スケールに配置することもできます。この標準スケールを使用すると、そうでなければ困難な観測値を比較できます。
このプロセスは標準化と呼ばれ、観測を比較し、さまざまな集団にわたって確率を計算できます。言い換えれば、リンゴとオレンジを比較することができます。統計は素晴らしいものではありません!
データを標準化するには、生の測定値をZスコアに変換する必要があります。
観測の標準スコアを計算するには、生の測定値を取り、平均を差し引き、標準偏差で除算します。数学的には、そのプロセスの式は次のとおりです。
z = { displaystyle frac { text {x} - mu} { sigma}}
xは、対象の測定の生の値を表します。 MuとSigmaは、観測が描かれた母集団のパラメーターを表します。
データを標準化した後、標準の正規分布内に配置できます。この方法で、標準化により、各観測が独自の分布内にある場所に基づいて、さまざまなタイプの観測を比較できます。標準スコアを使用してリンゴとオレンジと比較する例
文字通り、リンゴをオレンジと比較したいとします。具体的には、その重みを比較しましょう。体重110グラムのリンゴと、重量が100グラムのオレンジがあると想像してください。
生の値を比較すると、リンゴの重量がオレンジよりも多いことがわかります。ただし、標準スコアを比較しましょう。これを行うには、リンゴとオレンジの重量分布の特性を知る必要があります。リンゴとオレンジの重量が次のパラメーター値を持つ正規分布に従うと仮定します:リンゴオレンジは平均重量グラム100 140標準偏差15 25 25
次に、Zスコアを計算します。
Apple = 110-100/15 = 0.667
Orange = 100-140/25 = -1.6
Apple(0.667)のZスコアは陽性です。つまり、リンゴは平均的なリンゴよりも重量が多いことを意味します。それは決して極度の価値ではありませんが、リンゴの平均を超えています。一方、オレンジにはZスコアがかなり陰性です(-1.6)。オレンジの平均重量をはるかに下回っています。これらのz値を以下の標準正規分布に配置しました。
Zスコアを使用してリンゴとオレンジを比較する標準正規分布のグラフ。
私たちのリンゴは私たちのオレンジよりも多くの重さですが、私たちは平均的なリンゴよりもやや重いものを実に陽気なオレンジ色と比較しています! Zスコアを使用して、各果物が独自の分布内にどのように適合するか、そしてそれらが互いにどのように比較されるかを学びました。正規分布の曲線下の領域を見つける
正規分布は確率分布です。確率分布と同様に、確率分布プロットの2つの点の間の曲線に該当する面積の割合は、値がその間隔内に収まる確率を示します。このプロパティの詳細については、確率分布の理解についての私の投稿をご覧ください。
通常、統計ソフトウェアを使用して、曲線の下の領域を見つけます。ただし、正規分布を使用して値を標準スコアに変換する場合、標準の正規分布テーブルでZスコアを調べて領域を計算できます。
異なる数の通常の分布が無限にあるため、パブリッシャーは分布ごとにテーブルを印刷できません。ただし、値を正規分布からZスコアに変換し、標準スコアの表を使用して確率を計算できます。 Zスコアのテーブルを使用します
AppleのZスコアを使用して(0.667)、それを使用してその重量パーセンタイルを決定しましょう。パーセンタイルは、特定の値を下回る人口の割合です。その結果、パーセンタイルを決定するには、0.667未満のZスコアの範囲に対応する領域を見つける必要があります。以下の表の一部では、当社のZスコアに最も近いZスコアは0.65で、これを使用します。
写真は、標準スコア(Zスコア)のテーブルの一部を示しています。
これらのテーブルのトリックは、値を正規分布のプロパティと組み合わせて使用して、必要な確率を計算することです。テーブル値は、-0.65と+0.65の間の曲線の面積が48.43%であることを示しています。しかし、それは私たちが知りたいことではありません。 0.65のZスコア未満の領域が必要です。
正規分布の2つの半分は、互いの鏡像であることがわかっています。したがって、-0.65および+0.65からの間隔の面積が48.43%の場合、0〜 +0.65の範囲はその半分でなければなりません:48.43/2 = 24.215%。さらに、ゼロ未満のすべてのスコアの面積が分布の半分(50%)であることがわかっています。
したがって、すべてのスコアの面積は0.65 = 50% + 24.215%= 74.215%= 74.215%
私たちのリンゴは約74パーセンタイルです。
以下は、同じパーセンタイルと、曲線下の対応する領域のグラフィカルな表現を示す統計ソフトウェアによって生成される確率分布プロットです。ソフトウェアは0.667のより正確な値を使用し、テーブルから0.65のZスコアを使用したため、値はわずかに異なります。
Zスコアを使用してパーセンタイルをグラフィカルに表示する確率分布プロット。正規分布が重要である他の理由
上記のすべてに加えて、統計で正規分布が重要である他のいくつかの理由があります。
Some statistical hypothesis tests assume that the data follow a normal distribution. However, as I explain in my post about parametric and nonparametric tests, there’s more to it than only whether the data are normally distributed.
Linear and nonlinear regression both assume that the residuals follow a normal distribution. Learn more in my post about assessing residual plots.
The central limit theorem states that as the sample size increases, the sampling distribution of the mean follows a normal distribution even when the underlying distribution of the original variable is non-normal.
それは正規分布についてかなりのことでした!うまくいけば、アナリストがそれを使用する多くの方法のためにそれが重要であることを理解できることを願っています。
出典:https://statisticsbyjim.com/basics/normal-distribution/

期待値0と標準偏差1の正規分布の累積確率1: 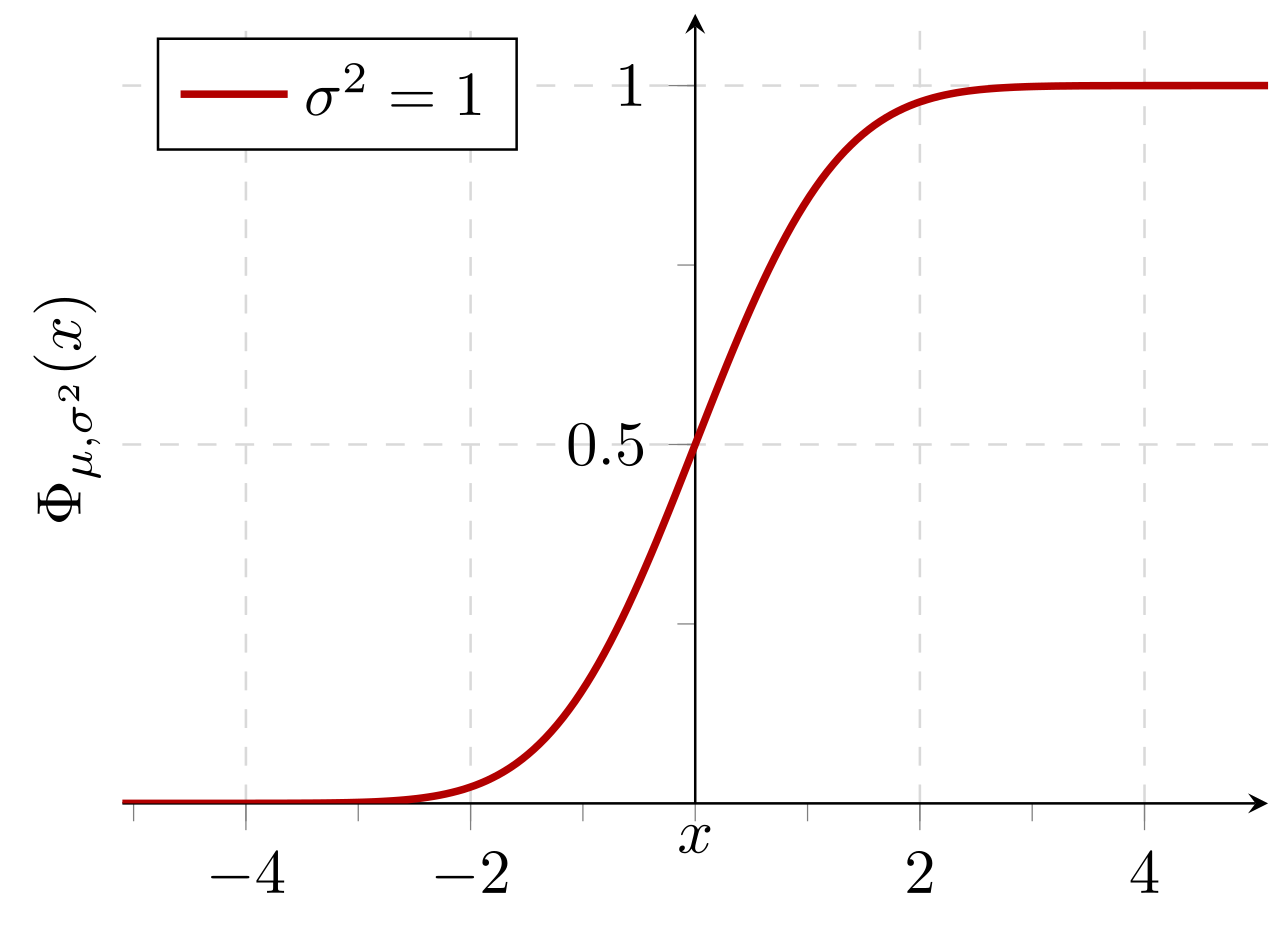
これは、パブリックドメインにリリースされた無料で妨げられていないソフトウェアです。詳細については、ライセンスファイルを参照してください。
ハビエル・カニョンが❤§で作られています。