SQL Server Нормальное распределение, гаусс или колокол кривой
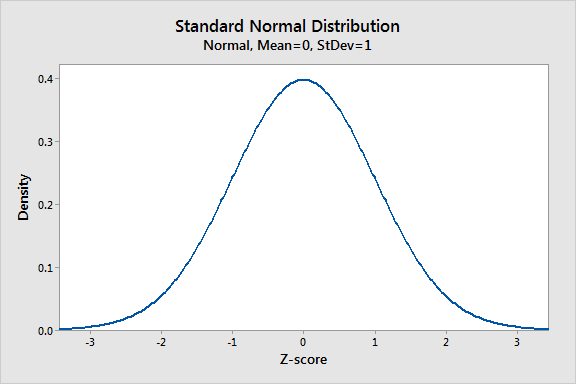
Нормальное распределение является наиболее важным распределением вероятностей в статистике, поскольку оно соответствует многим природным явлениям. Например, высота, артериальное давление, ошибка измерения и оценки IQ следуют нормальному распределению. Он также известен как гауссовое распределение и кривая колокола.
Нормальное распределение - это вероятностная функция, которая описывает, как распределяются значения переменной. Это симметричное распределение, в котором большинство наблюдений кластера вокруг центрального пика и вероятностей для значений дальше от среднего конуса в равной степени в обоих направлениях. Экстремальные значения в обоих хвостах распределения маловероятны.
В этом блоге вы узнаете, как использовать обычное распределение, его параметры и как вычислять Z-оценки для стандартизации ваших данных и найти вероятности. Пример нормально распределенных данных: высоты
Данные высоты обычно распределены. Распределение в этом примере соответствует реальным данным, которые я собрал у 14-летних девочек во время исследования.
Нормальное распределение высот.
Как вы можете видеть, распределение высот следует за типичной шаблоном для всех нормальных распределений. Большинство девушек близки к среднему (1,512 метра). Небольшие различия между высотой индивидуума и средним значением встречаются чаще, чем существенные отклонения от среднего. Стандартное отклонение составляет 0,0741 м, что указывает на типичное расстояние, которое отдельные девушки, как правило, падают от средней высоты.
Распределение симметрично. Число девочек короче среднего равна количеству девочек выше среднего. В обоих хвостах распределения очень короткие девушки встречаются так же редко, как очень высокие девушки. Параметры нормального распределения
Как и в случае любого распределения вероятностей, параметры для нормального распределения определяют его форму и вероятности. Нормальное распределение имеет два параметра, среднее и стандартное отклонение. Нормальное распределение не имеет только одной формы. Вместо этого форма изменяется на основе значений параметров, как показано на графиках ниже. Иметь в виду
Среднее значение является центральной тенденцией распределения. Он определяет местоположение пика для нормальных распределений. Большинство значений объединяются вокруг среднего. На графике изменение среднего смещения всей кривой влево или вправо на оси X.
График, который отображает нормальные распределения с разными средствами. Стандартное отклонение
Стандартное отклонение является мерой изменчивости. Он определяет ширину нормального распределения. Стандартное отклонение определяет, насколько далеко от среднего значения имеют тенденцию падать. Он представляет собой типичное расстояние между наблюдениями и средним.
На графике изменение стандартного отклонения либо подтягивает или распределяет ширину распределения вдоль оси X. Большие стандартные отклонения дают распределения, которые более распространены.
График, который отображает нормальные распределения с различными стандартными отклонениями.
Когда у вас есть узкие распределения, вероятности выше, что значения не падают далеко от среднего. По мере увеличения распространения распределения вероятность того, что наблюдения будут дальше от среднего значения. Параметры популяции по сравнению с оценками выборки
Среднее и стандартное отклонение - это значения параметров, которые применяются ко всем популяциям. Для нормального распределения статистики означают параметры с использованием греческого символа μ (mu) для среднего значения популяции и σ (Sigma) для стандартного отклонения популяции.
К сожалению, параметры населения обычно неизвестны, потому что обычно невозможно измерить целую популяцию. Тем не менее, вы можете использовать случайные выборы для расчета оценок этих параметров. Статистики представляют оценки выборки этих параметров с использованием x̅ для среднего и S для стандартного отклонения выборки.
Связанные посты: меры центральной тенденции и показателей изменчивости Общие свойства для всех форм нормального распределения
Несмотря на различные формы, все формы нормального распределения имеют следующие характерные свойства.
They’re all symmetric. The normal distribution cannot model skewed distributions.
The mean, median, and mode are all equal.
Half of the population is less than the mean and half is greater than the mean.
The Empirical Rule allows you to determine the proportion of values that fall within certain distances from the mean. More on this below!
Хотя нормальное распределение имеет важное значение в статистике, оно является лишь одним из многих распределений вероятностей, и оно не соответствует всем населению. Чтобы узнать, как определить, обеспечивает ли нормальное распределение наилучшим образом соответствовать данным вашего образца, прочитайте мои посты о том, как определить распределение ваших данных и оценку нормальности: гистограммы по сравнению с нормальной вероятностью. Эмпирическое правило для нормального распределения
Когда у вас обычно распределенные данные, стандартное отклонение становится особенно ценным. Вы можете использовать его для определения доли значений, которые попадают в указанное количество стандартных отклонений от среднего. Например, в нормальном распределении 68% наблюдений попадают в стандартное отклонение от +/- 1. Это свойство является частью эмпирического правила, которое описывает процент данных, которые подпадают под определенное количество стандартных отклонений от среднего значения для кривых колокольчиков. Среднее значение +/- Процент стандартных отклонений данных, содержащих 1 68% 2 95% 3 99,7%
Давайте посмотрим на пример доставки пиццы. Предположим, что в ресторане Pizza среднее время доставки 30 минут и стандартное отклонение в 5 минут. Используя эмпирическое правило, мы можем определить, что 68% сроков доставки составляют от 25 до 35 минут (30 +/- 5), 95% составляют 20-40 минут (30 +/- 2 5), а 99,7%-между 15-45 минутами (30 +/- 3 5). Диаграмма ниже иллюстрирует это свойство графически.
График, который отображает нормальное распределение с областями, разделенными на стандартные отклонения. Стандартное нормальное распределение и стандартные оценки
Как мы видели выше, нормальное распределение имеет много разных форм в зависимости от значений параметров. Тем не менее, стандартное нормальное распределение является особым случаем нормального распределения, где среднее значение равно нулю, а стандартное отклонение-1. Это распределение также известно как z-распределение.
Значение на стандартном нормальном распределении известно как стандартная оценка или Z-оценка. Стандартная оценка представляет количество стандартных отклонений выше или ниже среднего значения, которое падает конкретное наблюдение. Например, стандартная оценка 1,5 указывает на то, что наблюдение составляет 1,5 стандартных отклонений выше среднего. С другой стороны, отрицательная оценка представляет значение ниже среднего. Среднее значение имеет Z-оценку 0.
График, который отображает стандартное нормальное распределение.
Предположим, вы весите яблоко, и оно весит 110 граммов. Невозможно сказать только по весу, как это яблоко сравнивает с другими яблоками. Однако, как вы увидите, после того, как вы рассчитаете его Z-оценку, вы знаете, где он падает относительно других яблок. Стандартизация: как вычислять z-показатели
Стандартные оценки - отличный способ понять, где находится конкретное наблюдение относительно всего распределения. Они также позволяют вам принимать наблюдения, взятые из обычно распределенных популяций, которые имеют различные средства и стандартные отклонения, и поместить их в стандартную масштабу. Эта стандартная шкала позволяет сравнить наблюдения, которые в противном случае были бы затруднены.
Этот процесс называется стандартизацией, и он позволяет сравнивать наблюдения и рассчитывать вероятности в разных популяциях. Другими словами, это позволяет вам сравнивать яблоки с апельсинами. Разве статистика не отличная!
Чтобы стандартизировать ваши данные, вам необходимо преобразовать необработанные измерения в Z-оценки.
Чтобы вычислить стандартную оценку для наблюдения, принять необработанное измерение, вычесть среднее значение и делить на стандартное отклонение. Математически формула для этого процесса является следующей:
Z = { displaystyle frac { text {x} - mu} { sigma}}
X представляет собой необработанное значение интереса измерения. MU и Sigma представляют параметры для популяции, из которой было проведено наблюдение.
После стандартизации ваших данных вы можете разместить их в стандартном нормальном распределении. Таким образом, стандартизация позволяет сравнивать различные типы наблюдений на основе того, где каждое наблюдение попадает в собственное распределение. Пример использования стандартных результатов для сравнения яблок с апельсинами
Предположим, мы буквально хотим сравнить яблоки с апельсинами. В частности, давайте сравним их веса. Представьте, что у нас есть яблоко, которое весит 110 граммов и апельсин, который весит 100 граммов.
Если мы сравним необработанные значения, легко увидеть, что яблоко весит больше, чем оранжевое. Тем не менее, давайте сравним их стандартные оценки. Для этого нам нужно знать свойства распределения веса для яблок и апельсинов. Предположим, что веса яблок и апельсинов следуют нормальному распределению со следующими значениями параметров: яблоки апельсины Средние граммы 100 140 Стандартное отклонение 15 25
Теперь мы рассчитаем Z-оценки:
Apple = 110-100/15 = 0.667
Orange = 100-140/25 = -1.6
Z-показатель для Apple (0,667) положительна, что означает, что наше яблоко весит больше, чем среднее яблоко. Это не крайнее значение ни в коем случае, но оно выше среднего для яблок. С другой стороны, апельсин имеет довольно отрицательный Z-показатель (-1,6). Это намного ниже среднего веса для апельсинов. Я поместил эти z-значения в стандартном нормальном распределении ниже.
График стандартного нормального распределения, которое сравнивает яблоки с апельсинами с использованием Z-показателя.
В то время как наше яблоко весит больше, чем на нашем апельсине, мы сравниваем несколько тяжелее, чем среднее яблоко с явно маленьким оранжевым оранжевым! Используя Z-оценки, мы узнали, как каждый фрукт вписывается в его собственное распределение и как они сравниваются друг с другом. Поиск областей под кривой нормального распределения
Нормальное распределение является распределением вероятностей. Как и в случае любого распределения вероятности, доля площади, которая подпадает под кривую между двумя точками на графике распределения вероятности, указывает на вероятность того, что значение попадет в этот интервал. Чтобы узнать больше об этом свойстве, прочитайте мой пост о понимании распределений вероятностей.
Как правило, я использую статистическое программное обеспечение для поиска областей под кривой. Однако, когда вы работаете с нормальным распределением и преобразовываете значения в стандартные оценки, вы можете рассчитать области, изучая Z-оценки в стандартной таблице нормального распределения.
Поскольку существует бесконечное количество различных нормальных распределений, издатели не могут распечатать таблицу для каждого распределения. Тем не менее, вы можете преобразовать значения из любого нормального распределения в Z-оценки, а затем использовать таблицу стандартных баллов для расчета вероятностей. Использование таблицы Z-оценки
Давайте возьмем Z-оценку для нашего Apple (0,667) и используем его, чтобы определить его процентиль веса. Процентил - это доля населения, которая падает ниже определенного значения. Следовательно, чтобы определить процентиль, нам нужно найти область, которая соответствует диапазону Z-показателей, которые составляют менее 0,667. В той части таблицы ниже, ближайший z-показатель на нашем составляет 0,65, который мы будем использовать.
Фотография показывает часть таблицы стандартных баллов (z-баллы).
Хитрость с этими таблицами состоит в том, чтобы использовать значения в сочетании со свойствами нормального распределения для расчета необходимой вероятности. Значение таблицы указывает, что площадь кривой от -0,65 до +0,65 составляет 48,43%. Однако это не то, что мы хотим знать. Мы хотим, чтобы область, которая меньше, чем Z-показатель 0,65.
Мы знаем, что две половинки нормального распределения являются зеркальными изображениями друг друга. Таким образом, если площадь для интервала от -0,65 и +0,65 составляет 48,43%, то диапазон от 0 до +0,65 должен составлять половину от этого: 48,43/2 = 24,215%. Кроме того, мы знаем, что площадь для всех баллов менее нуля составляет половину (50%) распределения.
Следовательно, площадь для всех оценок до 0,65 = 50% + 24,215% = 74,215%
Наше яблоко находится примерно на 74 -м процентиле.
Ниже приведен график распределения вероятностей, созданный статистическим программным обеспечением, который показывает тот же процентиль вместе с графическим представлением соответствующей области под кривой. Значение немного отличается, потому что мы использовали Z-показатель 0,65 из таблицы, в то время как программное обеспечение использует более точное значение 0,667.
График распределения вероятностей, который графически отображает процентиль с использованием Z-показателя. Другие причины, по которым нормальное распределение важно
В дополнение ко всем вышеперечисленным, есть несколько других причин, по которым нормальное распределение имеет решающее значение в статистике.
Some statistical hypothesis tests assume that the data follow a normal distribution. However, as I explain in my post about parametric and nonparametric tests, there’s more to it than only whether the data are normally distributed.
Linear and nonlinear regression both assume that the residuals follow a normal distribution. Learn more in my post about assessing residual plots.
The central limit theorem states that as the sample size increases, the sampling distribution of the mean follows a normal distribution even when the underlying distribution of the original variable is non-normal.
Это было немного о нормальном распределении! Надеемся, что вы можете понять, что это имеет решающее значение из -за многих способов, которыми аналитики его используют.
Источник: https://statisticsbyjim.com/basics/normal-distribution/

Кумулятивная вероятность нормального распределения с ожидаемым значением 0 и стандартным отклонением 1: 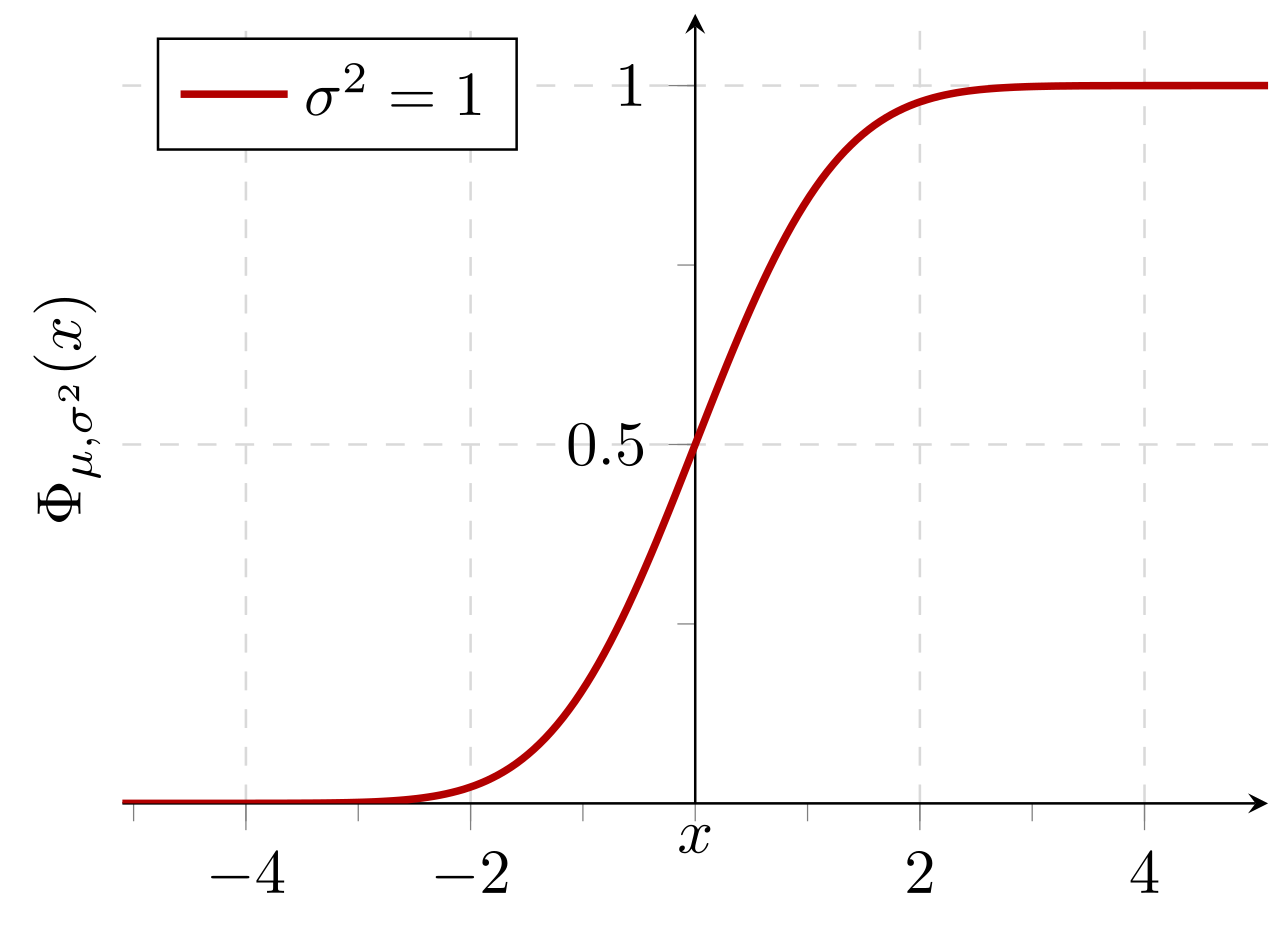
Это бесплатное и незаключенное программное обеспечение, выпущенное в общедоступном домене - для получения подробной информации см. Файл лицензии.
Сделано с ❤ Хавьер Каньон.