SQL Server正态分布,高斯或钟形曲线
正态分布是统计中最重要的概率分布,因为它符合许多自然现象。例如,高度,血压,测量误差和智商得分遵循正态分布。它也被称为高斯分布和钟形曲线。
正态分布是描述变量值分布的概率函数。这是一个对称分布,其中大多数观测值都集中在中心峰周围,并且在两个方向上平均锥度均匀偏离平均锥度的值概率。分布的两个尾巴中的极端值也不太可能。
在此博客文章中,您将学习如何使用正常分布,其参数以及如何计算z得分以标准化数据并找到概率。正态分布数据的示例:高度
高度数据是正态分布的。此示例中的分布符合我在研究期间从14岁女孩那里收集的真实数据。
高度的正态分布。
如您所见,高度的分布遵循所有正常分布的典型模式。大多数女孩接近平均水平(1.512米)。一个人的身高和平均值之间的差异小于与平均值的实质性偏差。标准偏差为0.0741m,这表明单个女孩往往会从平均身高下降的典型距离。
分布是对称的。女子的人数短于平均水平,等于高于平均水平的女孩人数。在分布的两个尾巴中,极度短的女孩的出现很少像极高的女孩一样。正态分布的参数
与任何概率分布一样,正态分布的参数完全定义其形状和概率。正态分布具有两个参数,平均值和标准偏差。正态分布不仅具有一种形式。相反,形状基于参数值会更改,如下图所示。意思是
平均值是分布的核心趋势。它定义了正常分布的峰位置。大多数值集中在均值周围。在图上,更改均值将整个曲线移动在X轴上向左或向右移动。
以不同方式显示正常分布的图。标准偏差
标准偏差是可变性的度量。它定义了正态分布的宽度。标准偏差决定了距离平均值往往会下降多远。它代表观测值和平均值之间的典型距离。
在图表上,更改标准偏差可以收紧或沿X轴分布的宽度。较大的标准偏差会产生更分布的分布。
图表显示出具有不同标准偏差的正常分布。
当您的分布狭窄时,概率较高,即值不会远离平均值。随着您增加分布的传播,观察结果远离平均值的可能性也会增加。人口参数与样本估计值
平均值和标准偏差是适用于整个人群的参数值。对于正态分布,统计学家通过使用希腊符号μ(MU)来表示参数,用于种群平均值,σ(Sigma)用于人口标准偏差。
不幸的是,人口参数通常是未知的,因为通常不可能衡量整个人口。但是,您可以使用随机样本来计算这些参数的估计值。统计学家代表这些参数的样本估计值,用于样品平均值和样本标准偏差的样本均值。
相关文章:正态分布的各种形式的中心趋势和可变性的衡量标准
尽管形状不同,但所有形式的正态分布都具有以下特征性能。
They’re all symmetric. The normal distribution cannot model skewed distributions.
The mean, median, and mode are all equal.
Half of the population is less than the mean and half is greater than the mean.
The Empirical Rule allows you to determine the proportion of values that fall within certain distances from the mean. More on this below!
尽管正态分布在统计中至关重要,但它只是许多概率分布之一,并且不符合所有种群。要了解如何确定正态分布是否为您的样本数据提供最佳拟合,请阅读有关如何识别数据分布并评估正态性的文章:直方图与正常概率图。正态分布的经验规则
当您正常分布数据时,标准偏差将变得特别有价值。您可以使用它来确定属于指定数量的标准偏差与平均值的值的比例。例如,在正态分布中,有68%的观测值属于+/- 1与平均值的标准偏差。该属性是经验规则的一部分,该属性描述了与钟形曲线平均值的特定数量偏差数在特定的标准偏差之内的数据百分比。平均+/-标准偏差百分比包含1 68%2 95%3 99.7%
让我们看一个披萨送货示例。假设一家披萨餐厅的平均交货时间为30分钟,标准偏差为5分钟。使用经验规则,我们可以确定68%的输送时间在25-35分钟之间(30 +/- 5),95%在20-40分钟之间(30 +/- 2 5),而99.7%在15-45分钟之间(30 +/- 3 5)。下图以图形方式说明了此属性。
图表显示正态分布,区域除以标准偏差。标准正态分布和标准分数
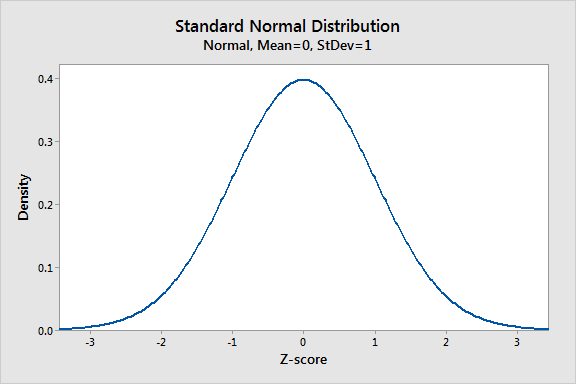
如上所述,正态分布具有许多不同的形状,具体取决于参数值。但是,标准正态分布是平均值为零且标准偏差为1的正态分布的特殊情况。此分布也称为z分布。
标准正态分布的值称为标准分数或z得分。标准分数表示特定观察值下降的平均值以上或低于平均值的标准偏差数量。例如,标准分数为1.5,表明该观察值高于平均值1.5标准偏差。另一方面,负分数代表低于平均值的值。平均值为0。
图表显示标准正态分布。
假设您称重苹果,重110克。从一个苹果与其他苹果相比,没有办法从重量中分辨出来。但是,如您所见,在计算其Z分数后,您知道它相对于其他苹果的位置。标准化:如何计算z得分
标准分数是了解特定观察结果相对于整个分布的何处的好方法。它们还允许您从具有不同手段和标准偏差的正态分布中提取的观察结果,并将其放置在标准尺度上。该标准秤使您能够比较原本很难的观察结果。
此过程称为标准化,它允许您比较观察结果并计算不同人群的概率。换句话说,它允许您将苹果与橘子进行比较。统计不大!
为了标准化数据,您需要将原始测量值转换为Z分数。
要计算观察的标准分数,请进行原始测量,减去平均值并除以标准偏差。从数学上讲,该过程的公式如下:
z = { displaystyle frac { text {x} - mu} { sigma}}}}
x表示兴趣测量的原始价值。 MU和Sigma代表了从中绘制观测值的人群的参数。
标准化数据后,您可以将它们放置在标准正态分布中。通过这种方式,标准化使您可以根据每个观测值属于其自身分布的位置比较不同类型的观测值。使用标准分数将苹果进行橙色比较的示例
假设我们想将苹果与橙子进行比较。具体来说,让我们比较自己的体重。想象一下,我们有一个重110克的苹果和一个重100克的橙色。
如果我们比较原始值,很容易看到苹果的重量比橙色重。但是,让我们比较他们的标准分数。为此,我们需要了解苹果和橘子的重量分布的属性。假设苹果和橙子的权重遵循正态分布,其参数值以下:苹果橙平均重量克100 140标准偏差15 25
现在,我们将计算Z分数:
Apple = 110-100/15 = 0.667
Orange = 100-140/25 = -1.6
苹果的Z分数(0.667)为正,这意味着我们的苹果的重量大于普通苹果。无论如何,这都不是极端价值,但是苹果的平均水平高于平均水平。另一方面,橙色的z得分相当负(-1.6)。它远低于橘子的平均重量。我将这些Z值放在下面的标准正态分布中。
使用z评分将苹果与橙色进行比较的标准正态分布图。
虽然我们的苹果的重量比橙色重,但我们的苹果比平均苹果更重的苹果与彻头彻尾的微弱的橙色进行了比较!使用Z分数,我们已经了解了每个果实如何适合其自身分布以及它们如何相互比较。在正态分布的曲线下查找区域
正态分布是概率分布。与任何概率分布一样,在概率分布图上属于两个点之间的曲线面积的比例表明值将值在该间隔内。要了解有关此属性的更多信息,请阅读我有关理解概率分布的文章。
通常,我使用统计软件来查找曲线下的区域。但是,当您使用正态分布并将值转换为标准分数时,您可以通过在标准正态分布表中查找z得分来计算区域。
由于存在无限数量的不同正常分布,因此发布者无法为每个分布打印一张表。但是,您可以将值从任何正常分布转换为z得分,然后使用标准分数表来计算概率。使用z得分表
让我们对苹果(0.667)进行Z分数,并使用它来确定其重量百分位。百分位数是人口的比例低于特定价值。因此,要确定百分位数,我们需要找到与小于0.667的Z分数范围相对应的区域。在下表的部分中,我们最接近我们的z得分为0.65,我们将使用。
照片显示了标准分数表(z得分)的一部分。
这些表的诀窍是将值与正态分布的属性结合使用来计算所需的概率。表值表明-0.65和+0.65之间的曲线面积为48.43%。但是,这不是我们想知道的。我们希望该区域小于Z得分为0.65。
我们知道正态分布的两个半分布是彼此的镜像。因此,如果间隔为-0.65和+0.65的区域为48.43%,则范围从0到+0.65,必须是其中的一半:48.43/2 = 24.215%。此外,我们知道所有分数小于零的面积是分布的一半(50%)。
因此,所有分数的面积高达0.65 = 50% + 24.215%= 74.215%
我们的苹果大约是第74个百分位数。
以下是统计软件产生的概率分布图,该图显示了相同的百分位数以及曲线下相应区域的图形表示。该值略有不同,因为我们使用表格为0.65,而软件则使用更精确的值为0.667。
使用Z分数以图形方式显示百分位数的概率分布图。正态分布很重要的其他原因
除了上述所有内容外,正态分布在统计数据中至关重要的其他原因有很多。
Some statistical hypothesis tests assume that the data follow a normal distribution. However, as I explain in my post about parametric and nonparametric tests, there’s more to it than only whether the data are normally distributed.
Linear and nonlinear regression both assume that the residuals follow a normal distribution. Learn more in my post about assessing residual plots.
The central limit theorem states that as the sample size increases, the sampling distribution of the mean follows a normal distribution even when the underlying distribution of the original variable is non-normal.
这是关于正态分布的很多!希望您可以理解,这是至关重要的,因为分析师使用它的多种方式。
资料来源:https://statistissbyjim.com/basics/normal-distribution/

具有期望值0和标准偏差的正态分布的累积概率1: 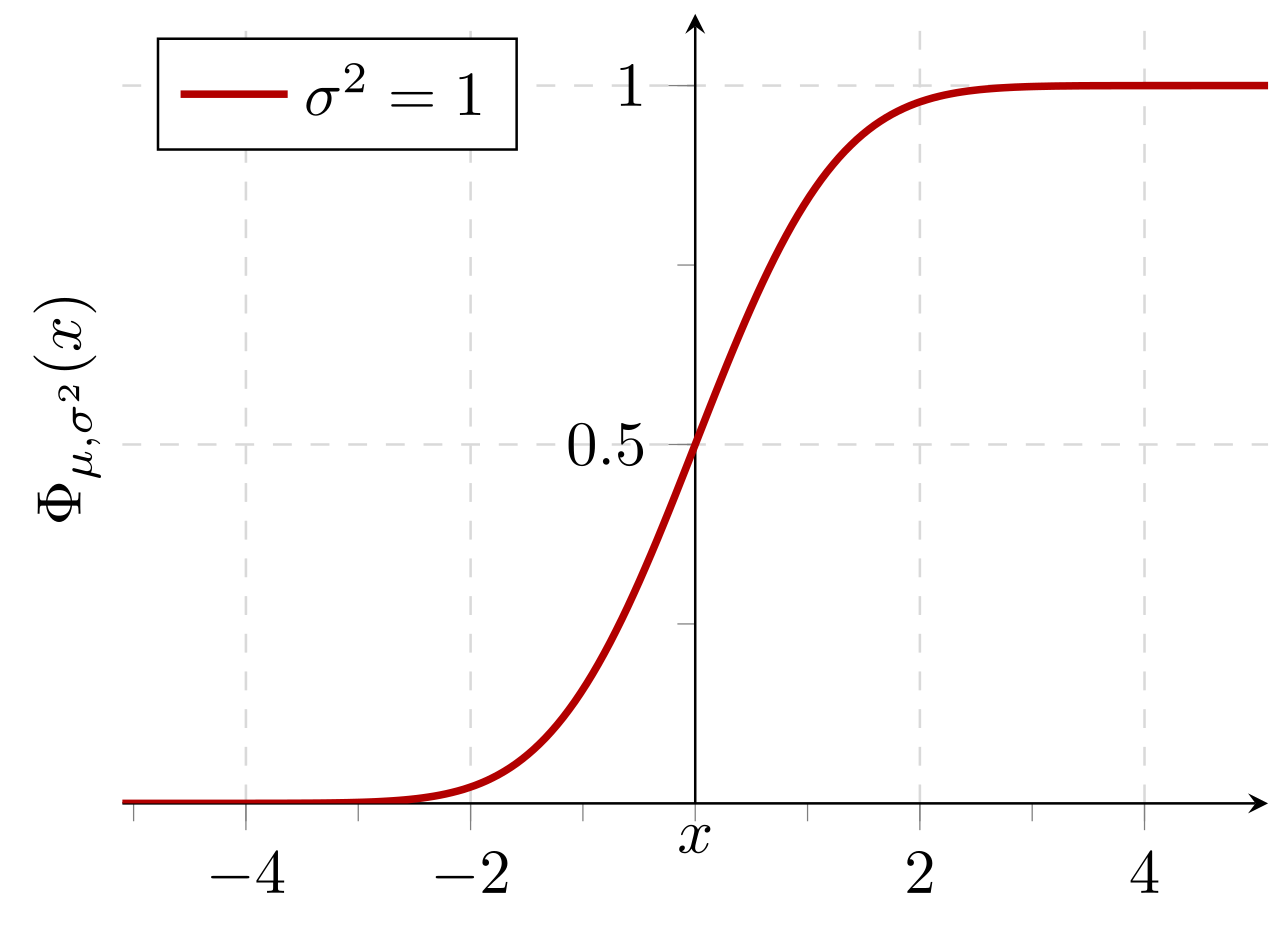
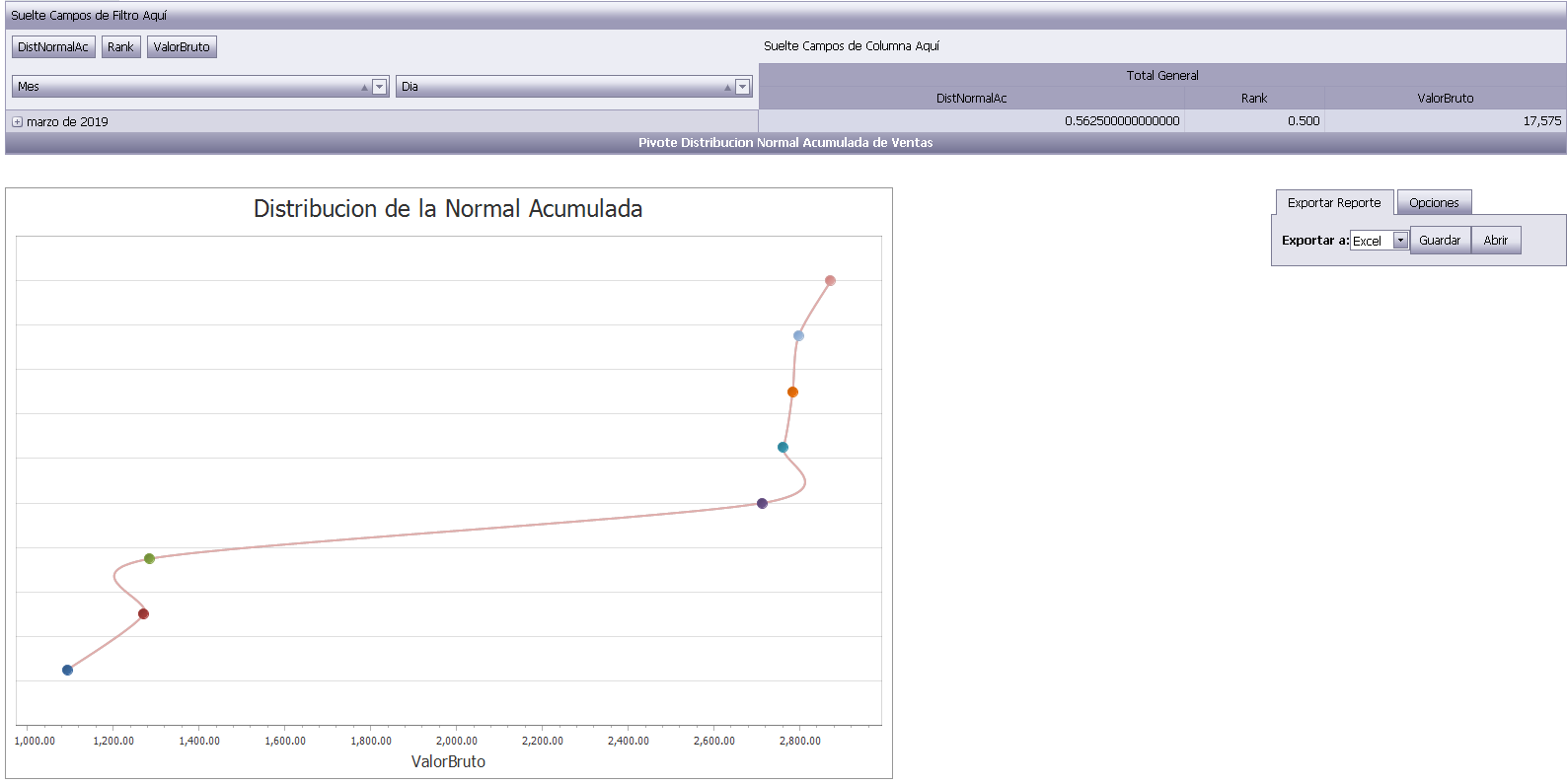
这是免费且无限制的软件,发布到公共领域 - 有关详细信息,请参见许可证文件。
由JavierCañon制成的。