SQL Server التوزيع العادي ، منحنى Gauss أو Bell
التوزيع الطبيعي هو أهم توزيع احتمال في الإحصائيات لأنه يناسب العديد من الظواهر الطبيعية. على سبيل المثال ، تتبع الارتفاعات وضغط الدم وخطأ القياس وعشرات الذكاء التوزيع الطبيعي. ومن المعروف أيضًا باسم التوزيع الغوسي ومنحنى الجرس.
التوزيع الطبيعي هو وظيفة احتمال تصف كيفية توزيع قيم المتغير. إنه توزيع متماثل حيث تتجمع معظم الملاحظات حول الذروة المركزية واحتمالات القيم بعيدًا عن المتوسط المتوسط على قدم المساواة في كلا الاتجاهين. القيم المتطرفة في كل من ذيول التوزيع غير مرجحة بالمثل.
في منشور المدونة هذا ، ستتعلم كيفية استخدام التوزيع العادي والمعلمات الخاصة به وكيفية حساب Scors لتوحيد بياناتك وإيجاد الاحتمالات. مثال على البيانات الموزعة عادة: مرتفعات
عادة ما يتم توزيع بيانات الارتفاع. يناسب التوزيع في هذا المثال بيانات حقيقية جمعتها من فتيات يبلغن من العمر 14 عامًا خلال دراسة.
التوزيع الطبيعي للارتفاعات.
كما ترون ، يتبع توزيع المرتفعات النمط النموذجي لجميع التوزيعات العادية. معظم الفتيات قريبة من المتوسط (1.512 متر). تحدث الاختلافات الصغيرة بين ارتفاع الفرد والمتوسط بشكل متكرر أكثر من الانحرافات الكبيرة عن الوسط. الانحراف المعياري هو 0.0741m ، مما يشير إلى المسافة النموذجية التي تميل الفتيات الفرديات إلى الانخفاض من متوسط الارتفاع.
التوزيع متماثل. عدد الفتيات الأقصر من المتوسط يساوي عدد الفتيات أطول من المتوسط. في كل من ذيول التوزيع ، تحدث الفتيات القصيرة للغاية مثل الفتيات طويل القامة للغاية. معلمات التوزيع الطبيعي
كما هو الحال مع أي توزيع احتمال ، تحدد المعلمات للتوزيع الطبيعي شكلها واحتمالاتها بالكامل. التوزيع الطبيعي له معلمتان ، المتوسط والانحراف المعياري. التوزيع الطبيعي ليس لديه نموذج واحد فقط. بدلاً من ذلك ، يتغير الشكل بناءً على قيم المعلمة ، كما هو موضح في الرسوم البيانية أدناه. يقصد
المتوسط هو الاتجاه المركزي للتوزيع. يحدد موقع الذروة للتوزيعات العادية. معظم القيم تتجمع حول الوسط. على الرسم البياني ، يؤدي تغيير المتوسط إلى تحول المنحنى بالكامل إلى اليسار أو اليمين على المحور السيني.
الرسم البياني الذي يعرض التوزيعات العادية بوسائل مختلفة. الانحراف المعياري
الانحراف المعياري هو مقياس للتغير. يحدد عرض التوزيع الطبيعي. يحدد الانحراف المعياري إلى أي مدى تميل القيم إلى السقوط. إنه يمثل المسافة النموذجية بين الملاحظات والمتوسط.
على الرسم البياني ، يؤدي تغيير الانحراف المعياري إلى تشديد أو انتشار عرض التوزيع على طول المحور السيني. تنتج الانحرافات المعيارية الأكبر توزيعات أكثر انتشارًا.
الرسم البياني الذي يعرض توزيعات طبيعية مع انحرافات معيارية مختلفة.
عندما يكون لديك توزيعات ضيقة ، تكون الاحتمالات أعلى من أن القيم لن تنخفض بعيدًا عن الوسط. مع زيادة انتشار التوزيع ، فإن احتمالية أن تكون الملاحظات ستكون بعيدًا عن المتوسط أيضًا. المعلمات السكانية مقابل تقديرات العينة
المتوسط والانحراف المعياري هما قيم المعلمات التي تنطبق على السكان بأكمله. بالنسبة للتوزيع الطبيعي ، يدل الإحصائيون إلى المعلمات باستخدام الرمز اليوناني μ (MU) للسكان الوسط و σ (Sigma) للانحراف المعياري للسكان.
لسوء الحظ ، عادة ما تكون معلمات السكان غير معروفة لأنه من المستحيل عمومًا قياس عدد السكان بأكمله. ومع ذلك ، يمكنك استخدام عينات عشوائية لحساب تقديرات هذه المعلمات. يمثل الإحصائيون تقديرات عينة من هذه المعلمات باستخدام X̅ لمعرفة العينة و S للانحراف المعياري للعينة.
الوظائف ذات الصلة: مقاييس الاتجاه المركزي ومقاييس التباين خصائص شائعة لجميع أشكال التوزيع الطبيعي
على الرغم من الأشكال المختلفة ، فإن جميع أشكال التوزيع الطبيعي لها الخصائص المميزة التالية.
They’re all symmetric. The normal distribution cannot model skewed distributions.
The mean, median, and mode are all equal.
Half of the population is less than the mean and half is greater than the mean.
The Empirical Rule allows you to determine the proportion of values that fall within certain distances from the mean. More on this below!
على الرغم من أن التوزيع الطبيعي ضروري في الإحصاءات ، إلا أنه واحد من توزيعات الاحتمالات العديدة ، ولا يناسب جميع المجموعات السكانية. لمعرفة كيفية تحديد ما إذا كان التوزيع العادي يوفر أفضل ملاءمة لبيانات العينة الخاصة بك ، اقرأ مشاركاتي حول كيفية تحديد توزيع بياناتك وتقييم الحالة الطبيعية: الرسوم البيانية مقابل مخططات الاحتمالات العادية. القاعدة التجريبية للتوزيع الطبيعي
عندما يكون لديك البيانات الموزعة عادة ، يصبح الانحراف المعياري ذا قيمة خاصة. يمكنك استخدامه لتحديد نسبة القيم التي تقع ضمن عدد محدد من الانحرافات المعيارية عن الوسط. على سبيل المثال ، في التوزيع الطبيعي ، تقع 68 ٪ من الملاحظات ضمن الانحراف المعياري +/- 1 عن الوسط. هذه الخاصية هي جزء من القاعدة التجريبية ، التي تصف النسبة المئوية للبيانات التي تقع ضمن أعداد محددة من الانحرافات المعيارية عن المتوسط بالنسبة للمنحنيات على شكل جرس. الوسط +/- الانحرافات المعيارية المئوية للبيانات تحتوي على 1 68 ٪ 2 95 ٪ 3 99.7 ٪
دعونا نلقي نظرة على مثال توصيل البيتزا. افترض أن مطعم البيتزا لديه متوسط وقت توصيل قدره 30 دقيقة وانحراف معياري مدته 5 دقائق. باستخدام القاعدة التجريبية ، يمكننا تحديد أن 68 ٪ من أوقات التسليم تتراوح بين 25-35 دقيقة (30 +/- 5) ، 95 ٪ بين 20-40 دقيقة (30 +/- 2 5) ، و 99.7 ٪ بين 15-45 دقيقة (30 +/- 3 5). يوضح الرسم البياني أدناه هذه الخاصية بيانيا.
الرسم البياني الذي يعرض التوزيع الطبيعي مع المناطق مقسومة على الانحرافات المعيارية. التوزيع العادي القياسي والنتائج القياسية
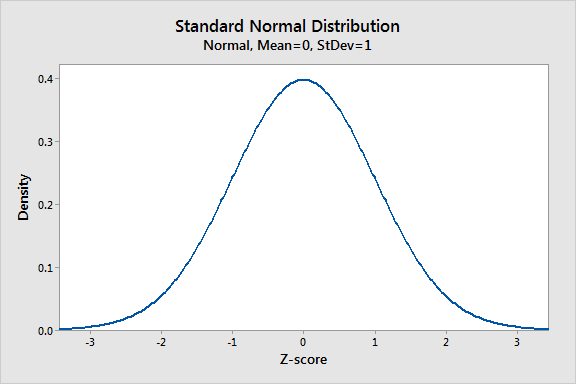
كما رأينا أعلاه ، فإن التوزيع الطبيعي له العديد من الأشكال المختلفة اعتمادًا على قيم المعلمة. ومع ذلك ، فإن التوزيع الطبيعي القياسي هو حالة خاصة للتوزيع الطبيعي حيث يكون الوسط صفرًا والانحراف المعياري هو 1. ويعرف هذا التوزيع أيضًا باسم التوزيع z.
تُعرف قيمة التوزيع العادي القياسي كنتيجة قياسية أو درجة Z. تمثل النتيجة القياسية عدد الانحرافات المعيارية أعلى أو أقل من يعني أن المراقبة المحددة تنخفض. على سبيل المثال ، تشير درجة قياسية قدرها 1.5 إلى أن الملاحظة هي 1.5 انحرافات معيارية أعلى من المتوسط. من ناحية أخرى ، تمثل النتيجة السلبية قيمة أقل من المتوسط. الوسط لديه درجة Z من 0.
الرسم البياني الذي يعرض التوزيع العادي القياسي.
لنفترض أنك تزن تفاحة وتزن 110 جرام. لا توجد طريقة لمعرفة من الوزن وحده كيف تقارن هذه التفاح بالتفاح الآخر. ومع ذلك ، كما سترى ، بعد حساب درجة Z ، أنت تعرف أين تقع بالنسبة إلى التفاح الآخر. التقييس: كيفية حساب الدرجات z
تعد الدرجات القياسية وسيلة رائعة لفهم المكان الذي تقع فيه ملاحظة معينة بالنسبة للتوزيع بأكمله. كما أنها تتيح لك الالتحاق بالملاحظات المستمدة من السكان الموزعة عادة التي لها وسائل مختلفة وانحرافات معيارية وتضعها على نطاق قياسي. يمكّنك هذا المقياس القياسي من مقارنة الملاحظات التي قد تكون صعبة.
تسمى هذه العملية التقييس ، وتتيح لك مقارنة الملاحظات وحساب الاحتمالات عبر مجموعات مختلفة. بمعنى آخر ، يسمح لك بمقارنة التفاح بالبرتقال. ليست إحصائيات رائعة!
لتوحيد بياناتك ، تحتاج إلى تحويل القياسات الأولية إلى درجات z.
لحساب النتيجة القياسية للمراقبة ، خذ القياس الخام ، وطرح الوسط ، وتقسيمه على الانحراف المعياري. رياضيا ، صيغة هذه العملية هي ما يلي:
z = { displaystyle frac { text {x} - mu} { sigma}}
X يمثل القيمة الخام لقياس الفائدة. يمثل MU و Sigma المعلمات للسكان الذين تم رسم الملاحظة منها.
بعد توحيد بياناتك ، يمكنك وضعها ضمن التوزيع العادي القياسي. وبهذه الطريقة ، يسمح لك التقييس بمقارنة أنواع مختلفة من الملاحظات بناءً على المكان الذي تقع فيه كل ملاحظة ضمن توزيعها. مثال على استخدام الدرجات القياسية لجعل التفاح إلى البرتقال مقارنة
لنفترض أننا نريد حرفيًا مقارنة التفاح بالبرتقال. على وجه التحديد ، دعنا نقارن أوزانهم. تخيل أن لدينا تفاحة تزن 110 جرامًا وبرتقالًا يزن 100 جرام.
إذا قمنا بمقارنة القيم الخام ، فمن السهل أن نرى أن التفاح يزن أكثر من البرتقال. ومع ذلك ، دعونا نقارن الدرجات القياسية. للقيام بذلك ، سنحتاج إلى معرفة خصائص توزيعات الوزن للتفاح والبرتقال. افترض أن أوزان التفاح والبرتقال تتبع التوزيع العادي مع قيم المعلمة التالية: برتقال التفاح يعني غرامات الوزن 100 140 الانحراف المعياري 15 25
الآن سنقوم بحساب الدرجات Z:
Apple = 110-100/15 = 0.667
Orange = 100-140/25 = -1.6
يعد درجة Z لـ Apple (0.667) إيجابية ، مما يعني أن تفاحةنا تزن أكثر من متوسط التفاح. إنها ليست قيمة متطرفة بأي وسيلة ، لكنها أعلى من المتوسط بالنسبة للتفاح. من ناحية أخرى ، فإن اللون البرتقالي لديه درجة Z سلبية إلى حد ما (-1.6). إنه أقل بكثير من متوسط الوزن للبرتقال. لقد وضعت هذه القيم z في التوزيع الطبيعي القياسي أدناه.
رسم بياني لتوزيع عادي قياسي يقارن التفاح بالبرتقال باستخدام درجة Z.
على الرغم من أن تفاحةنا تزن أكثر من برتقالي ، إلا أننا نقارن أثقل إلى حد ما من التفاح المتوسط إلى برتقالي بصراحة! باستخدام الدرجات Z ، تعلمنا كيف تناسب كل فاكهة ضمن توزيعها الخاص وكيفية مقارنة بعضها البعض. إيجاد مناطق تحت منحنى التوزيع الطبيعي
التوزيع الطبيعي هو توزيع احتمال. كما هو الحال مع أي توزيع احتمال ، تشير نسبة المساحة التي تقع تحت المنحنى بين نقطتين في مؤامرة توزيع الاحتمالات إلى احتمال أن تقع القيمة خلال تلك الفاصل الزمني. لمعرفة المزيد حول هذه الخاصية ، اقرأ رسالتي حول فهم توزيعات الاحتمالات.
عادةً ما أستخدم البرامج الإحصائية للعثور على مناطق تحت المنحنى. ومع ذلك ، عندما تعمل مع التوزيع العادي وتحويل القيم إلى درجات قياسية ، يمكنك حساب المناطق من خلال البحث عن درجات Z في جدول توزيع عادي قياسي.
نظرًا لوجود عدد لا حصر له من التوزيعات العادية المختلفة ، لا يمكن للناشرين طباعة جدول لكل توزيع. ومع ذلك ، يمكنك تحويل القيم من أي توزيع طبيعي إلى درجات z ، ثم استخدام جدول من الدرجات القياسية لحساب الاحتمالات. باستخدام جدول من الدرجات Z
دعنا نأخذ درجة Z ل Apple (0.667) ونستخدمها لتحديد نسبة الوزن. النسبة المئوية هي نسبة السكان التي تقل عن قيمة محددة. وبالتالي ، لتحديد النسبة المئوية ، نحتاج إلى العثور على المنطقة التي تتوافق مع نطاق الدرجات Z التي تقل عن 0.667. في الجزء من الجدول أدناه ، فإن أقرب درجة Z إلى نقاطنا هو 0.65 ، والتي سنستخدمها.
تُظهر الصورة جزءًا من جدول الدرجات القياسية (الدرجات Z).
تتمثل الخدعة مع هذه الجداول في استخدام القيم بالتزامن مع خصائص التوزيع العادي لحساب الاحتمال الذي تحتاجه. تشير قيمة الجدول إلى أن مساحة المنحنى بين -0.65 و +0.65 هي 48.43 ٪. ومع ذلك ، هذا ليس ما نريد معرفته. نريد المنطقة التي تقل عن درجة Z من 0.65.
نحن نعلم أن نصفي التوزيع العادي هما صور مرآة لبعضها البعض. لذلك ، إذا كانت مساحة الفاصل الزمني من -0.65 و +0.65 هي 48.43 ٪ ، فيجب أن يكون النطاق من 0 إلى +0.65 نصف ذلك: 48.43/2 = 24.215 ٪. بالإضافة إلى ذلك ، نعلم أن المنطقة لجميع الدرجات التي تقل عن الصفر هي نصف (50 ٪) من التوزيع.
لذلك ، فإن المنطقة لجميع الدرجات تصل إلى 0.65 = 50 ٪ + 24.215 ٪ = 74.215 ٪
تفاحة لدينا في ما يقرب من 74 المئوية.
فيما يلي مؤامرة توزيع الاحتمالات التي تنتجها البرامج الإحصائية التي تُظهر نفس المئوية إلى جانب تمثيل رسومي للمنطقة المقابلة تحت المنحنى. تختلف القيمة قليلاً لأننا استخدمنا درجة Z من 0.65 من الجدول بينما يستخدم البرنامج القيمة الأكثر دقة 0.667.
مؤامرة توزيع الاحتمالات التي تعرض بيانياً مئوية باستخدام درجة Z. أسباب أخرى تجعل التوزيع الطبيعي مهمًا
بالإضافة إلى كل ما سبق ، هناك العديد من الأسباب الأخرى التي تجعل التوزيع الطبيعي أمرًا بالغ الأهمية في الإحصاءات.
Some statistical hypothesis tests assume that the data follow a normal distribution. However, as I explain in my post about parametric and nonparametric tests, there’s more to it than only whether the data are normally distributed.
Linear and nonlinear regression both assume that the residuals follow a normal distribution. Learn more in my post about assessing residual plots.
The central limit theorem states that as the sample size increases, the sampling distribution of the mean follows a normal distribution even when the underlying distribution of the original variable is non-normal.
كان ذلك قليلاً عن التوزيع العادي! نأمل أن تفهم أنه أمر بالغ الأهمية بسبب العديد من الطرق التي يستخدمها المحللون.
المصدر: https://statisticsbyjim.com/basics/normal-distribution/

الاحتمال التراكمي للتوزيع الطبيعي مع القيمة المتوقعة 0 والانحراف المعياري 1: 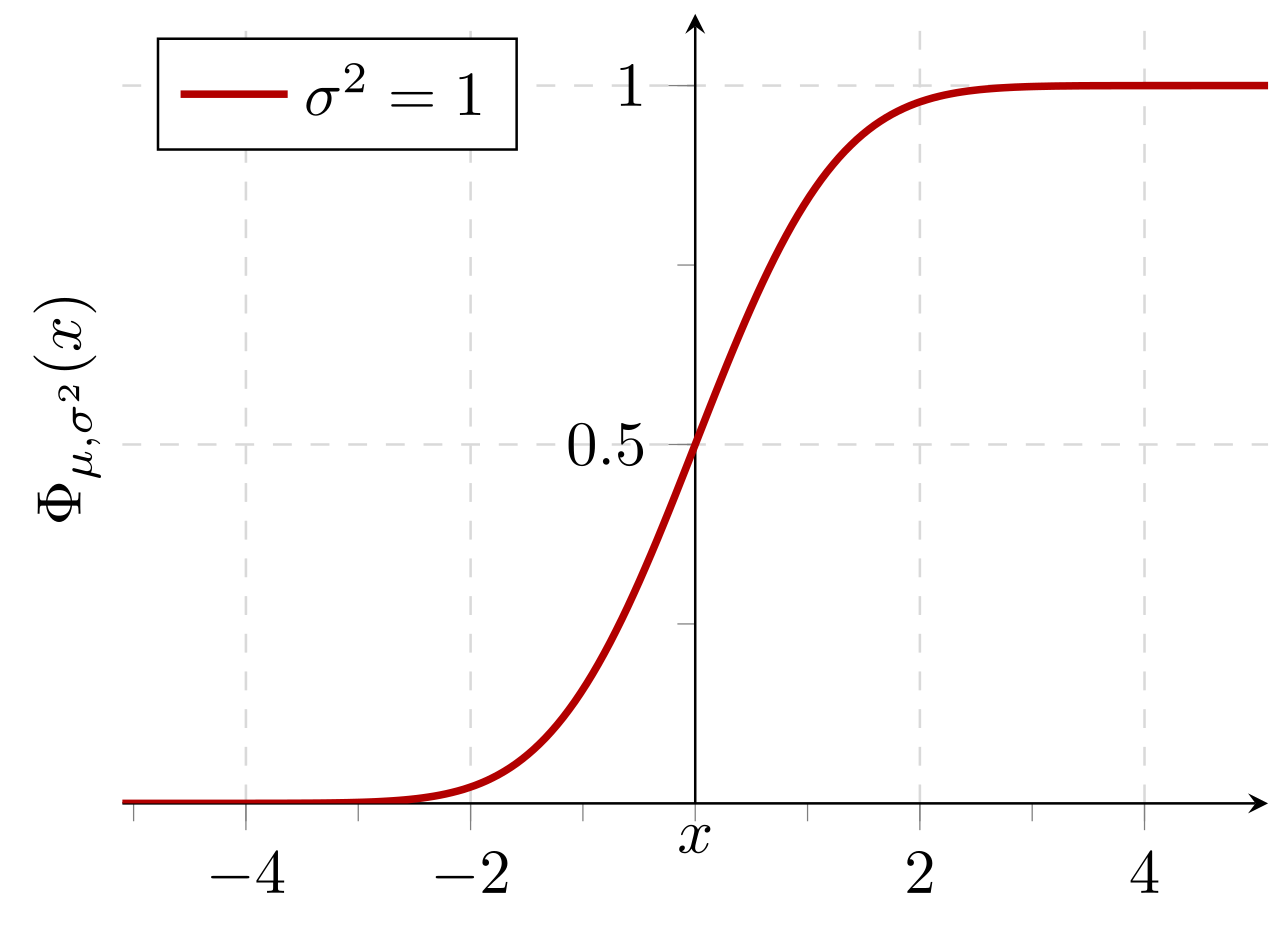
هذا برنامج مجاني وغير معروف تم إصداره في المجال العام - راجع ملف الترخيص للحصول على التفاصيل.
صنعت مع ❤ بواسطة خافيير كانون.