算法是由一組有限的指令組成的過程,該指令從某些可能的輸入中給出了輸入,使得能夠獲得輸出。
唐納德·諾斯(Donald Knuth):“計算機科學是算法的研究。 ”
插入排序是一種簡單的排序算法,其工作方式類似於您手中的撲克牌的方式。該數組實際上分為分類和未分類的部分。從分類部件中挑選未分類零件的值並將其放置在排序部分的正確位置。
注意:找到採摘元件的正確位置是另一種算法,我們必須通過比較和轉移來找到其位置,直到找到正確的位置。我在這裡註意到這一點,因為我記得第一次了解算法,尤其是對算法進行分類,總是想到很高的水平,因此,我認為我沒有理解甚至設計算法的思想。
我拍攝了以下圖像,介紹了Wikipedia插入算法的工作方式。此外,還有許多其他網站(例如VisualGo)可視化這些算法和數據結構。
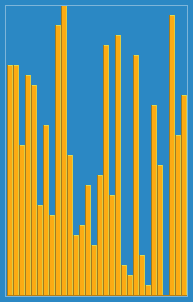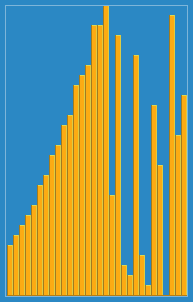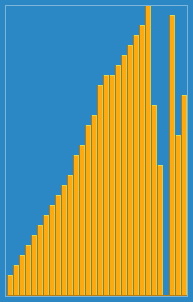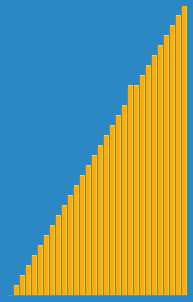
您可以在此處的Python中找到此算法的源代碼。該算法的複雜性為O(n 2 ),因為它由兩個嵌套環組成。
該排序算法是一種分裂和爭議算法,該算法將數組分為兩個半數組,然後對它們進行分類後,將它們合併以再次構建整個數組。以下示例取自Wikipedia。
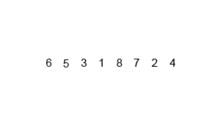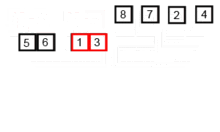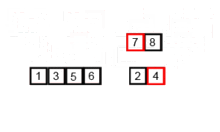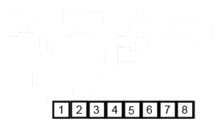
您可以在此處的Python中找到此算法的源代碼。該算法的複雜性為O(nlogn)。複雜性的視野是,因為在該算法的每個步驟中,每個陣列的長度都分為兩個子陣列,因此我們有一棵具有LOGN高度的操作樹,而且因為在樹的每個級別中,我們必須合併兩個子陣列,需要在n元素上進行n元素的循環,以便algorithm的複雜性(nx logn)。
要了解複雜性的重要性,並且對O(n2)的速度( n2 )的速度快,也會生成一個輸入文件夾中的輸入文件,然後將其輸入到算法中。只需去測試它們,看看它們之間的執行時間差即可。
數學分析中的漸近分析,漸近分析(也稱為漸近分析)是一種描述限制行為的方法。在分析算法複雜性時,我們將此方法通常使用o符號通常比較算法。您可以看到一些示例如下:
n 2 + 5n + 10 = o(n 2 )
log3(n)= O(log2(n))
log(n!)= log(n *(n -1) * ... * 1)= logn + log(n -1) + log(n -2) + ... + ... + log2 + log1 = o(nlogn)
在下面的圖像中,我們可以清楚地看到符號。
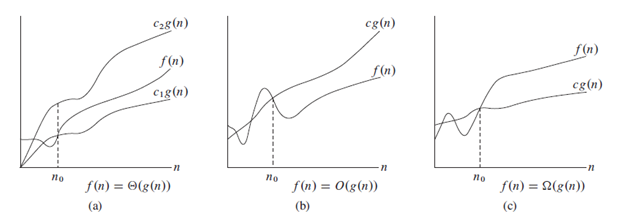
注意:使用O而不是TETA(科學上不正確)是對話。
為了分析遞歸算法,我們可以通過考慮一棵樹和每一層所需的操作,然後將它們乘以它們來直觀地分析它們。但是,它不會一直工作。
主定理:在下面的圖像中,顯示了主定理,我們可以輕鬆地用於分析遞歸算法。但是,我們必須能夠編寫要分析的遞歸算法的遞歸方程。
