Ein Algorithmus ist ein Verfahren, das aus einem endlichen Satz von Anweisungen besteht, die es ermöglicht, eine Ausgabe zu erhalten.
Donald Knuth: „ Informatik ist das Studium von Algorithmen. “
Die Insertion -Sortierung ist ein einfacher Sortieralgorithmus, der der Art und Weise, wie Sie Karten in Ihren Händen sortieren, ähnelt. Das Array ist praktisch in einen sortierten und ungeortierten Teil aufgeteilt. Werte aus dem ungeortierten Teil werden ausgewählt und an der richtigen Position im sortierten Teil platziert.
Hinweis : Das Finden des richtigen Ortes des ausgewählten Elements ist ein weiterer Algorithmus. Wir müssen seinen Platz finden, indem wir vergleichen und verschoben werden, bis er seinen richtigen Ort findet. Ich habe es hier bemerkt, weil ich mich erinnere, als ich zum ersten Mal etwas über Algorithmen lernte, insbesondere von einem Sortieren, immer so hoch und aus diesem Grund dachte ich, ich habe keinen Verstand, Algorithmen zu verstehen oder sogar zu entwerfen.
Ich machte das folgende Bild darüber, wie der Einfügungsalgorithmus aus Wikipedia funktioniert. Es gibt auch viele andere Websites wie Visualgo, die diese Algorithmen und auch Datenstrukturen visualisieren.
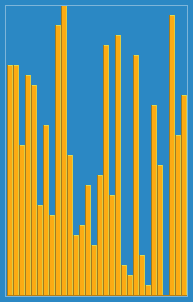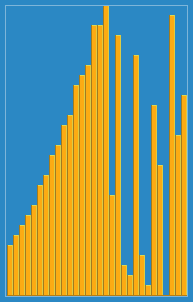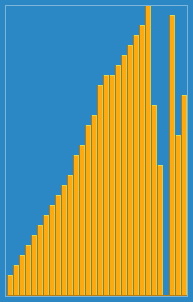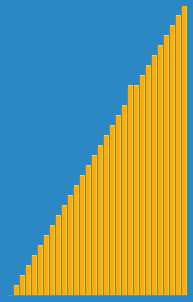
Hier finden Sie den Quellcode dieses Algorithmus in Python. Die Komplexität dieses Algorithmus beträgt O (n 2 ), da er aus zwei verschachtelten Schleifen besteht.
Dieser Sortieralgorithmus ist ein Divide-and-Conquer-Algorithmus, der ein Array in zwei halbe Arrays unterteilt und nach dem separaten Sortieren sie zusammen verschmilzt, um das gesamte Array erneut zu bauen. Das folgende Beispiel stammt aus Wikipedia.
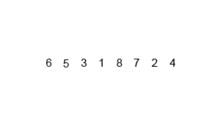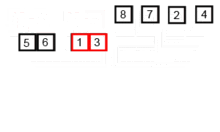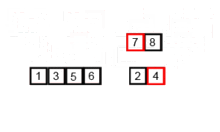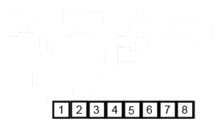
Hier finden Sie den Quellcode dieses Algorithmus in Python. Die Komplexität dieses Algorithmus ist O (NLOGN). Die Vision der Komplexität ist, dass, weil in jedem Schritt dieses Algorithmus jedes Array mit der Länge von N in zwei Subtarrays unterteilt ist und wir einen Operationsbaum mit lognischer Höhe haben, und auch, weil wir in jeder Ebene des Baumes zwei Subarrays fusionieren müssen, die eine Schleifenrunde auf Nelementen erfordern, so dass die Komplexität des Algorithmus (nx logn).
Um zu verstehen, wie wichtig die Komplexität ist und um auch ein Gefühl zu haben, wie viel schneller O (NLOGN) als O (N 2 ) ist, wird eine Eingabedatei mit 1M -Zufallszahlen im Eingabedordner generiert und dann den Algorithmen gefüttert. Gehen Sie einfach und testen Sie sie und sehen Sie den Unterschied zwischen ihnen aus.
Die asymptotische Analyse in der mathematischen Analyse, der asymptotischen Analyse, auch als Asymptotik bezeichnet, ist eine Methode zur Beschreibung des begrenzenden Verhaltens. Bei der Analyse der Komplexität der Algorithmen beziehen wir uns auf diese Methode, um Algorithmen im Allgemeinen mit O -Notation zu vergleichen. Sie können ein Beispiel wie folgt sehen:
n 2 + 5n + 10 = o (n 2 )
log3 (n) = o (log2 (n))
log (n!) = log (n * (n -1) * ... * 1) = logn + log (n - 1) + log (n - 2) + ... + log2 + log1 = o (nLogn)
Im folgenden Bild können wir die Notationen deutlich sehen.
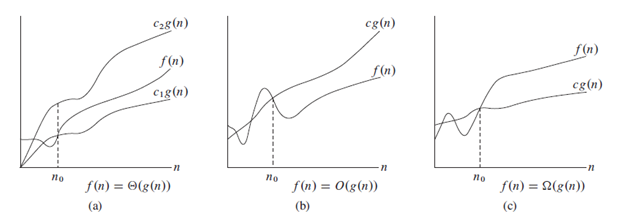
Hinweis : Es ist überzeugt, O anstelle von Teta (wissenschaftlich falsch) zu verwenden.
Zur Analyse rekursiver Algorithmen können wir sie intuitiv analysieren, indem wir einen Baum und die für jede Schicht benötigten Operationen berücksichtigen und sie einfach multiplizieren. Aber es wird nicht die ganze Zeit funktionieren.
Master -Theorem : Im folgenden Bild wird ein Master -Theorem gezeigt, mit dem wir unsere rekursiven Algorithmen problemlos analysieren können. Wir müssen jedoch in der Lage sein, die rekursive Gleichung des rekursiven Algorithmus zu schreiben, den wir analysieren möchten.
