アルゴリズムは、可能な入力のいくつかのセットからの入力が出力を取得できる有限の命令セットで構成される手順です。
Donald Knuth:「コンピューターサイエンスはアルゴリズムの研究です。 」
挿入ソートは、トランプを手に並べ替える方法と同様に機能する単純なソートアルゴリズムです。アレイは、並べ替えられた部品と未解決の部分に実質的に分割されます。解散部品からの値は選択され、ソートされた部分の正しい位置に配置されます。
注:選択された要素の適切な場所を見つけることは別のアルゴリズムです。正しい場所を見つけるまで比較してシフトすることでその場所を見つける必要があります。アルゴリズム、特に並べ替えについて初めて学んだことを覚えているので、ここでそれを指摘しました。
挿入アルゴリズムがウィキペディアからどのように機能するかについて、次の画像を撮影しました。また、これらのアルゴリズムとデータ構造を視覚化するVisualGoのような他の多くのWebサイトがあります。
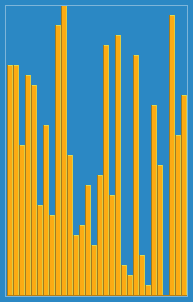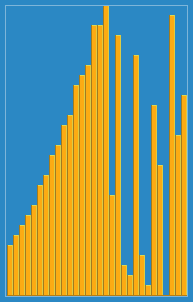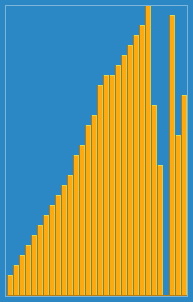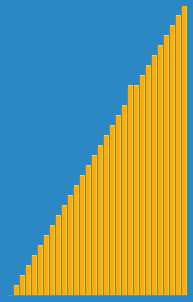
このアルゴリズムのソースコードは、Pythonでここで見つけることができます。このアルゴリズムの複雑さは、2つのネストされたループで構成されるため、O(n 2 )です。
このソートアルゴリズムは、分割アルゴリズムであり、配列を2つのハーフアレイに分割し、個別にソートした後、アレイ全体を再度構築します。次の例は、ウィキペディアから取得されています。
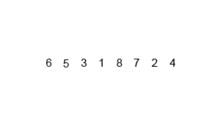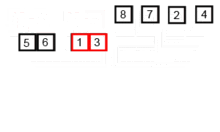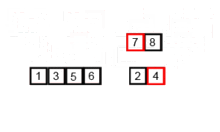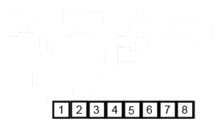
このアルゴリズムのソースコードは、Pythonでここで見つけることができます。このアルゴリズムの複雑さはO(nlogn)です。複雑さのビジョンは、このアルゴリズムの各ステップで、Nの長さを持つすべての配列が2つのサブアレイに分割されているため、logn heightの操作ツリーがあるため、ツリーの各レベルでは、n要素を必要とする2つのサブアレイをマージする必要があるためです。
複雑さがどれほど重要であるかを理解し、またO(nlogn)がO(n 2 )よりもどれだけ速いO(nlogn)であるかを理解するために、入力フォルダーに1Mランダム数を持つ入力ファイルが生成され、アルゴリズムに供給されます。行ってテストして、それらの間の実行時差を確認してください。
数学的分析における漸近分析、漸近性としても知られる漸近分析は、制限行動を記述する方法です。アルゴリズムの複雑さを分析する際に、一般的にO表記を使用して、一般的にアルゴリズムを比較できるようにこの方法を参照します。次の例を見ることができます。
n 2 + 5n + 10 = o(n 2 )
log3(n)= o(log2(n))
log(n!)= log(n *(n -1) * ... * 1)= logn + log(n -1) + log(n -2) + ... + log2 + log1 = o(nlogn)
次の画像では、表記をはっきりと見ることができます。
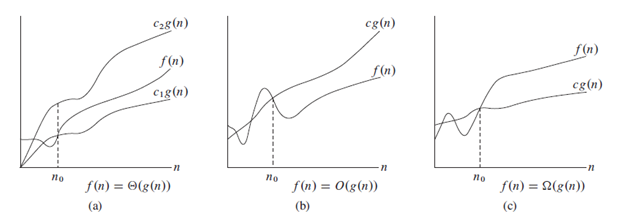
注:TETA(科学的に間違っている)の代わりにOを使用するのは可逆です。
再帰アルゴリズムを分析するために、各レイヤーで必要なツリーと操作を考慮して、それらを直感的に分析することができ、それらを掛けるだけです。しかし、それは常に機能しません。
マスター定理:次の画像には、マスター定理が表示されています。これを使用して、再帰アルゴリズムを分析するために簡単に使用できます。ただし、分析したい再帰アルゴリズムの再帰方程式を作成できる必要があります。
