Un algoritmo es un procedimiento que consiste en un conjunto finito de instrucciones que, dada la entrada de algún conjunto de posibles entradas, permite obtener una salida.
Donald Knuth: " La informática es el estudio de los algoritmos".
La clasificación de inserción es un algoritmo de clasificación simple que funciona de manera similar a la forma en que clasificas a las cartas en tus manos. La matriz se divide virtualmente en una parte ordenada y sin clasificar. Los valores de la parte no organizada se recogen y se colocan en la posición correcta en la parte ordenada.
Nota : Encontrar el lugar correcto del elemento seleccionado es otro algoritmo, tenemos que encontrar su lugar comparando y cambiando hasta encontrar su lugar correcto. Lo noté aquí porque recuerdo mientras que por primera vez aprendí sobre algoritmos, especialmente clasificando uno, siempre estaba pensando tan alto nivel y por eso, estaba pensando que no tengo la mente para entender o incluso diseñar algoritmos.
Tomé la siguiente imagen de cómo funciona el algoritmo de inserción de Wikipedia. Además, hay muchos otros sitios web como Visualgo que visualizan estos algoritmos y también estructuras de datos.
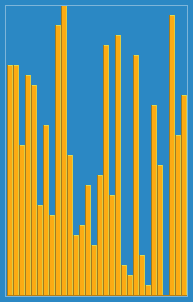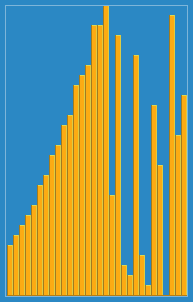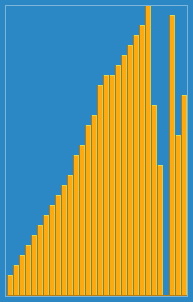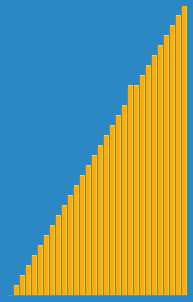
Puede encontrar el código fuente de este algoritmo en Python aquí. La complejidad de este algoritmo es O (n 2 ) porque consta de dos bucles anidados.
Este algoritmo de clasificación es un algoritmo de división y conquista, que divide una matriz en dos medias matrices, y después de clasificarlas por separado, los fusiona para construir toda la matriz nuevamente. El siguiente ejemplo se toma de Wikipedia.
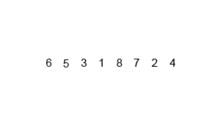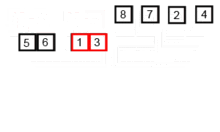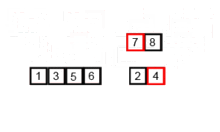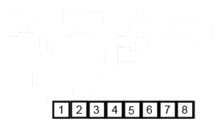
Puede encontrar el código fuente de este algoritmo en Python aquí. La complejidad de este algoritmo es O (NLOGN). La visión de la complejidad es que en cada paso de este algoritmo, cada matriz con la longitud de N se divide en 2 subarrays y, por lo tanto, tenemos un árbol de operaciones con altura de logn, y también porque en cada nivel del árbol tenemos que fusionar dos subarrías que requieren un bucle que iteran en los elementos de N para que la complejidad de algorithm (NX logn).
Para comprender lo importante que es la complejidad y también tener sentido sobre cuánto más rápido es (nLogn) que o (n 2 ), se genera un archivo de entrada con números aleatorios de 1M en la carpeta de entrada, luego se alimenta a los algoritmos. Simplemente vaya a probarlos y vea la diferencia de tiempo de ejecución entre ellos.
El análisis asintótico en el análisis matemático, el análisis asintótico, también conocido como asintótica, es un método para describir el comportamiento limitante. Al analizar la complejidad de los algoritmos, nos referimos a este método para poder comparar los algoritmos en general, utilizando la notación O en general. Puedes ver algún ejemplo de la siguiente manera:
n 2 + 5n + 10 = o (n 2 )
log3 (n) = o (log2 (n))
log (n!) = log (n * (n -1) * ... * 1) = logn + log (n - 1) + log (n - 2) + ... + log2 + log1 = o (nLogn)
En la siguiente imagen, podemos ver las anotaciones claramente.
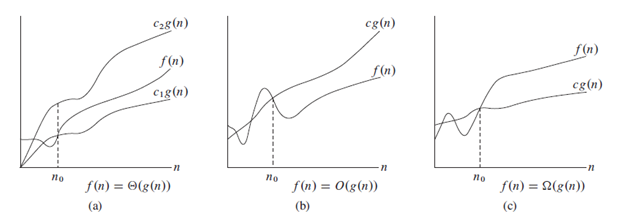
NOTA : Es la convención usar O en lugar de TETA (científicamente incorrecta).
Para analizar algoritmos recursivos, podemos analizarlos intuitivamente considerando un árbol y las operaciones necesarias en cada capa, y simplemente multiplicarlos. Pero, no va a funcionar todo el tiempo.
Teorema maestro : en la siguiente imagen, se muestra el teorema maestro, que podemos usar fácilmente para analizar nuestros algoritmos recursivos. Sin embargo, debemos poder escribir la ecuación recursiva del algoritmo recursivo que queremos analizar.
