Algoritma adalah prosedur yang terdiri dari serangkaian instruksi yang terbatas yang, diberikan input dari beberapa set input yang mungkin, memungkinkan untuk mendapatkan output.
Donald Knuth: " Ilmu Komputer adalah studi tentang algoritma. "
Penyisipan Sort adalah algoritma penyortiran sederhana yang berfungsi mirip dengan cara Anda mengurutkan kartu bermain di tangan Anda. Array hampir terbagi menjadi bagian yang disortir dan tidak disortir. Nilai -nilai dari bagian yang tidak disortir dipetik dan ditempatkan pada posisi yang benar di bagian yang diurutkan.
Catatan : Menemukan tempat yang tepat dari elemen yang dipetik adalah algoritma lain, kita harus menemukan tempatnya dengan membandingkan dan bergeser sampai menemukan tempat yang benar. Saya mencatatnya di sini karena saya ingat sementara untuk pertama kalinya saya belajar tentang algoritma, terutama menyortir satu, selalu saya berpikir sangat tinggi dan karena itu, saya berpikir saya tidak punya pikiran untuk memahami atau bahkan merancang algoritma.
Saya mengambil gambar berikut tentang cara kerja algoritma penyisipan dari Wikipedia. Juga, ada banyak situs web lain seperti VisualGo yang memvisualisasikan algoritma ini dan juga struktur data.
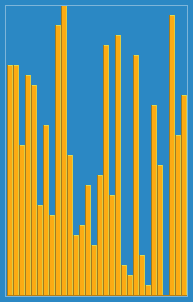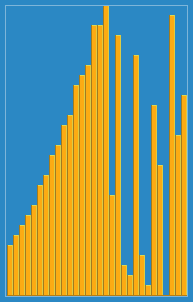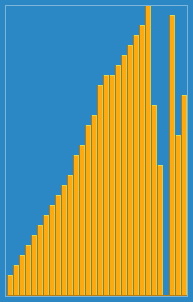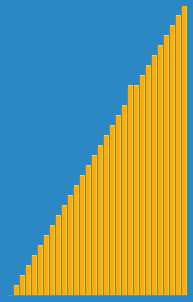
Anda dapat menemukan kode sumber algoritma ini di Python di sini. Kompleksitas algoritma ini adalah O (n 2 ) karena terdiri dari dua loop bersarang.
Algoritma penyortiran ini adalah algoritma pembagian-dan-penakluk, yang membagi array menjadi dua array setengah, dan setelah menyortirnya secara terpisah, menggabungkan mereka untuk membangun seluruh array lagi. Contoh berikut diambil dari Wikipedia.
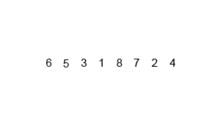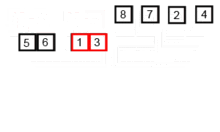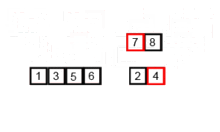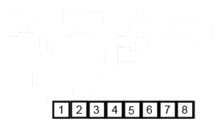
Anda dapat menemukan kode sumber algoritma ini di Python di sini. Kompleksitas algoritma ini adalah O (nlogn). Visi kompleksitas adalah bahwa karena dalam setiap langkah algoritma ini setiap array dengan panjang n dibagi menjadi 2 subarray sehingga kami memiliki pohon operasi dengan tinggi logn, dan juga karena di setiap tingkat pohon kami harus menggabungkan dua subarray yang membutuhkan loop iterasi pada elemen n sehingga kompleksitas algoritma adalah (NX LOGN).
Untuk memahami betapa pentingnya kompleksitas dan juga memiliki perasaan tentang seberapa cepat O (nlogn) daripada O (n 2 ), file input dengan angka acak 1M dalam folder input dihasilkan, kemudian diumpankan ke algoritma. Pergi dan uji saja dan lihat perbedaan waktu eksekusi di antara mereka.
Analisis asimptotik dalam analisis matematika, analisis asimptotik, juga dikenal sebagai asimptotik, adalah metode menggambarkan perilaku pembatas. Dalam menganalisis kompleksitas algoritma, kami merujuk pada metode ini untuk dapat membandingkan algoritma umumnya, menggunakan notasi O secara umum. Anda dapat melihat beberapa contoh sebagai berikut:
n 2 + 5n + 10 = o (n 2 )
log3 (n) = o (log2 (n))
log (n!) = log (n * (n -1) * ... * 1) = LOGN + LOG (n - 1) + log (n - 2) + ... + log2 + log1 = o (nlogn)
Pada gambar berikut, kita dapat melihat notasi dengan jelas.
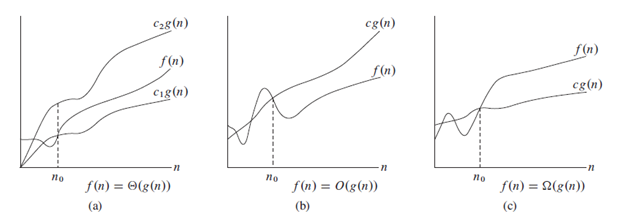
Catatan : Ini adalah konvensi untuk menggunakan O bukan TETA (secara ilmiah salah).
Untuk menganalisis algoritma rekursif, kami dapat menganalisisnya secara intuitif dengan mempertimbangkan pohon dan operasi yang diperlukan pada setiap lapisan, dan melipatgandakannya. Tapi, itu tidak akan bekerja sepanjang waktu.
Master Theorem : Dalam gambar berikut, Teorema Master ditampilkan, yang dapat dengan mudah kami gunakan untuk menganalisis algoritma rekursif kami. Namun, kami harus dapat menulis persamaan rekursif dari algoritma rekursif yang ingin kami analisis.
