Um algoritmo é um procedimento que consiste em um conjunto finito de instruções que, dada a entrada de algum conjunto de entradas possíveis, permite obter uma saída.
Donald Knuth: " A ciência da computação é o estudo de algoritmos".
O tipo de inserção é um algoritmo simples de classificação que funciona semelhante à maneira como você classifica as cartas de jogo em suas mãos. A matriz é praticamente dividida em uma parte classificada e não classificada. Os valores da parte não classificada são colhidos e colocados na posição correta na parte classificada.
Nota : Encontrar o local certo do elemento escolhido é outro algoritmo, temos que encontrar seu lugar comparando e mudando até encontrar seu lugar correto. Eu notei isso aqui porque me lembro que, pela primeira vez, aprendi sobre algoritmos, especialmente classificando um, sempre estava pensando em nível tão alto e, por causa disso, estava pensando que não tenho uma mente para entender ou mesmo projetar algoritmos.
Tirei a seguinte imagem de como o algoritmo de inserção funciona da Wikipedia. Além disso, existem muitos outros sites como o Visualgo que visualiza esses algoritmos e também as estruturas de dados.
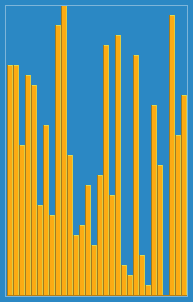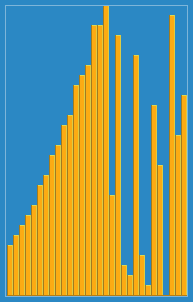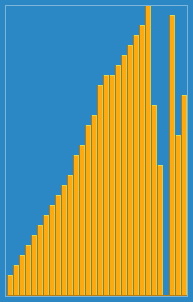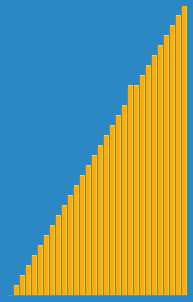
Você pode encontrar o código -fonte desse algoritmo no Python aqui. A complexidade desse algoritmo é O (n 2 ) porque consiste em dois loops aninhados.
Esse algoritmo de classificação é um algoritmo de divisão e conquista, que divide uma matriz em duas metades matrizes e, depois de classificá-las separadamente, mescla para construir a matriz inteira novamente. O exemplo a seguir é retirado da Wikipedia.
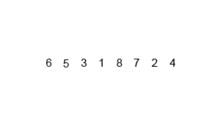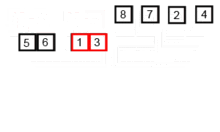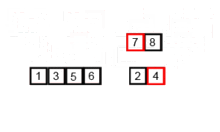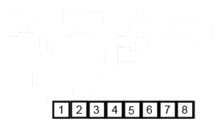
Você pode encontrar o código -fonte desse algoritmo no Python aqui. A complexidade desse algoritmo é O (nLogn). A visão da complexidade é que, porque em cada etapa deste algoritmo cada matriz com o comprimento de n é dividida em 2 subarrays e, portanto, temos uma árvore de operações com altura de logn, e também porque em cada nível da árvore precisamos mesclar dois subarray requer uma retenção de loop em n elementos, assim, a complexidade do algoritmo é (NX Logn).
Para entender o quão importante é a complexidade e também ter um senso de quanto mais rápido O (nLogn) é que O (n 2 ), um arquivo de entrada com números aleatórios de 1M na pasta de entrada é gerado e depois alimentado com os algoritmos. Basta testá -los e ver a diferença de tempo de execução entre eles.
Análise assintótica em análise matemática, análise assintótica, também conhecida como assintática, é um método para descrever o comportamento limitador. Ao analisar a complexidade dos algoritmos, nos referimos a esse método para poder comparar algoritmos geralmente, usando a notação O geralmente. Você pode ver algum exemplo da seguinte maneira:
n 2 + 5n + 10 = o (n 2 )
log3 (n) = o (log2 (n))
log (n!) = log (n * (n -1) * ... * 1) = logn + log (n - 1) + log (n - 2) + ... + log2 + log1 = o (nLogn)
Na imagem a seguir, podemos ver as anotações claramente.
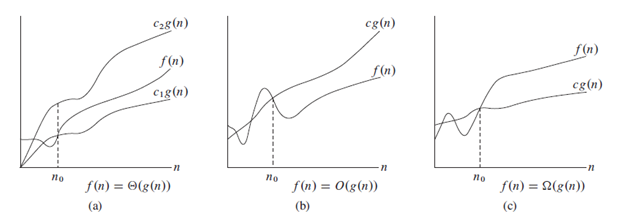
Nota : é convpensa usar o em vez de teta (cientificamente incorreto).
Para analisar algoritmos recursivos, podemos analisá -los intuitivamente, considerando uma árvore e as operações necessárias em cada camada e apenas multiplicá -las. Mas, não vai funcionar o tempo todo.
Teorema Master : Na imagem a seguir, é mostrado o teorema Master, que podemos usar facilmente para analisar nossos algoritmos recursivos. No entanto, precisamos escrever a equação recursiva do algoritmo recursivo que queremos analisar.
