알고리즘은 가능한 일부 입력 세트로부터 입력이 주어지면 출력을 얻을 수있는 유한 명령 세트로 구성된 절차입니다.
Donald Knuth :“ 컴퓨터 과학은 알고리즘에 대한 연구입니다. ”
삽입 정렬은 손에 카드 놀이를 정렬하는 방식과 유사하게 작동하는 간단한 정렬 알고리즘입니다. 배열은 사실상 정렬 된 부분으로 분리되어 있습니다. 분류되지 않은 부품의 값을 선택하고 정렬 된 부분의 올바른 위치에 배치합니다.
참고 : 선택한 요소의 올바른 장소를 찾는 것은 또 다른 알고리즘이므로 올바른 장소를 찾을 때까지 비교하고 이동하여 위치를 찾아야합니다. 나는 알고리즘, 특히 하나를 정렬하는 알고리즘에 대해 처음 배웠을 때 항상 너무 높은 수준을 생각하고 있었기 때문에 알고리즘을 이해하거나 설계 할 마음이 없다고 생각했습니다.
Wikipedia에서 삽입 알고리즘이 어떻게 작동하는지에 대한 다음 이미지를 찍었습니다. 또한 이러한 알고리즘과 데이터 구조를 시각화하는 VisualGo와 같은 다른 웹 사이트가 많이 있습니다.
이 알고리즘의 소스 코드를 Python에서 찾을 수 있습니다. 이 알고리즘의 복잡성은 두 개의 중첩 루프로 구성되기 때문에 O (n 2 )입니다.
이 분류 알고리즘은 분할 및 정체 알고리즘으로 배열을 두 개의 절반 어레이로 나누고 별도로 정렬 한 후 전체 배열을 다시 빌드하도록 합병합니다. 다음 예는 Wikipedia에서 가져 왔습니다.
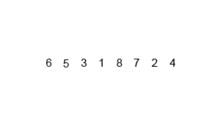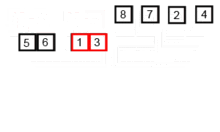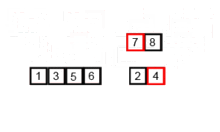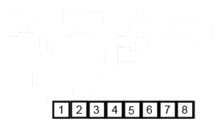
이 알고리즘의 소스 코드를 Python에서 찾을 수 있습니다. 이 알고리즘의 복잡성은 O (nlogn)입니다. 복잡성에 대한 비전은이 알고리즘의 각 단계에서 N 길이를 가진 모든 배열이 2 개의 서브 배열로 나뉘어 지므로 Logn 높이가있는 작업 트리가 있기 때문에 트리의 각 레벨에서는 N 요소에 루프를 반복 해야하는 두 개의 서브 어레이를 병합해야한다는 것입니다 (nx logn).
복잡성이 얼마나 중요한지 이해하고 O (Nlogn)가 O (n 2 )보다 얼마나 빠른 지에 대한 감각을 갖기 위해 입력 폴더에 1m 랜덤 숫자가 1m 인 입력 파일이 생성 된 다음 알고리즘에 공급됩니다. 그냥 가서 테스트하고 그들 사이의 실행 시간 차이를보십시오.
수학적 분석에서 점근 분석에서, 무증상으로 알려진 점근 분석은 제한 행동을 설명하는 방법이다. 알고리즘 복잡성을 분석 할 때 일반적으로 O 표기법을 사용하여 일반적으로 알고리즘을 비교할 수있는이 방법을 참조하십시오. 다음과 같이 몇 가지 예를 볼 수 있습니다.
n 2 + 5n + 10 = O (n 2 )
log3 (n) = O (log2 (n))
log (n!) = log (n * (n -1) * ... * 1) = logn + log (n -1) + log (n -2) + ... + log2 + log1 = O (nlogn)
다음 이미지에서는 표기법을 명확하게 볼 수 있습니다.
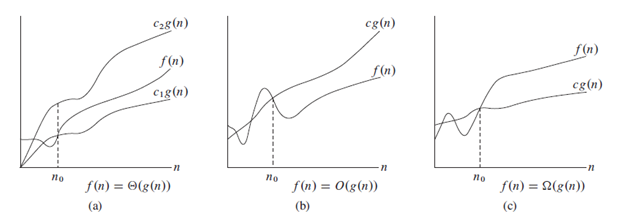
참고 : TETA 대신 O를 사용하는 것은 Convension입니다 (과학적으로 부정확).
재귀 알고리즘을 분석하기 위해 트리와 각 계층에 필요한 작업을 고려하여 직관적으로 분석하고 곱할 수 있습니다. 그러나 그것은 항상 작동하지 않을 것입니다.
마스터 정리 : 다음 이미지에 마스터 정리가 표시되며, 이는 재귀 알고리즘을 분석하는 데 쉽게 사용할 수 있습니다. 그러나 분석하려는 재귀 알고리즘의 재귀 방정식을 작성할 수 있어야합니다.
