Un algorithme est une procédure qui se compose d'un ensemble fini d'instructions qui, étant donné l'entrée d'un ensemble d'entrées possibles, permet d'obtenir une sortie.
Donald Knuth: « L'informatique est l'étude des algorithmes».
Le tri de l'insertion est un algorithme de tri simple qui fonctionne similaire à la façon dont vous triez les cartes à jouer entre vos mains. Le tableau est pratiquement divisé en une partie triée et non triée. Les valeurs de la pièce non triée sont choisies et placées à la position correcte dans la pièce triée.
Remarque : Trouver le bon endroit de l'élément choisi est un autre algorithme, nous devons trouver sa place en comparant et en changeant jusqu'à trouver son bon endroit. Je l'ai noté ici parce que je me souviens que pour la première fois que j'ai appris sur les algorithmes, en particulier en triant un, je pensais toujours si haut niveau et à cause de cela, je pensais que je n'ai pas l'esprit de comprendre ou même de concevoir des algorithmes.
J'ai pris l'image suivante de la façon dont l'algorithme d'insertion fonctionne de Wikipedia. En outre, il existe de nombreux autres sites Web comme VisualGo qui visualisent ces algorithmes ainsi que les structures de données.
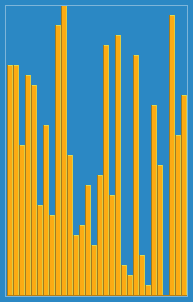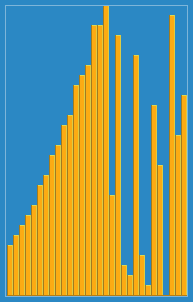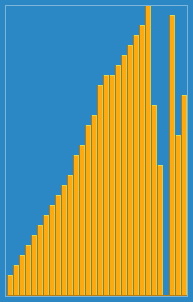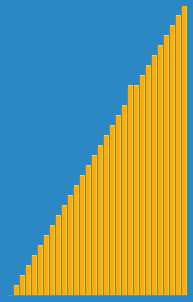
Vous pouvez trouver le code source de cet algorithme dans Python ici. La complexité de cet algorithme est O (n 2 ) car elle se compose de deux boucles imbriquées.
Cet algorithme de tri est un algorithme de division et de conquête, qui divise un tableau en deux demi-tableaux, et après les tris séparément, les fusionne pour construire à nouveau l'ensemble du tableau. L'exemple suivant est tiré de Wikipedia.
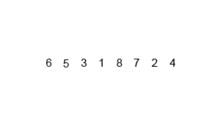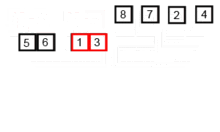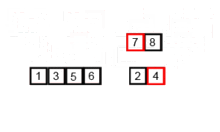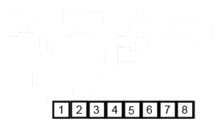
Vous pouvez trouver le code source de cet algorithme dans Python ici. La complexité de cet algorithme est O (nlogn). La vision de la complexité est que, car à chaque étape de cet algorithme, chaque tableau avec la longueur de N est divisé en 2 sous-réseaux et nous avons donc un arbre d'opérations à la hauteur de la logn, et aussi parce que dans chaque niveau de l'arbre, nous devons fusionner deux sous-rares nécessitant une boucle itérant sur n éléments.
Pour comprendre à quel point la complexité est importante et aussi pour avoir un sens sur la quantité d'O (nlogn) plus rapide qu'O (n 2 ), un fichier d'entrée avec 1M de nombres aléatoires dans le dossier d'entrée est généré, puis alimenté aux algorithmes. Allez simplement les tester et voyez le décalage horaire d'exécution entre eux.
L'analyse asymptotique dans l'analyse mathématique, l'analyse asymptotique, également connue sous le nom d'asymptotique, est une méthode de décrire le comportement limitant. En analysant la complexité des algorithmes, nous nous référons à cette méthode pour être en mesure de comparer les algorithmes généralement, en utilisant la notation O en général. Vous pouvez voir un exemple comme suit:
n 2 + 5n + 10 = o (n 2 )
log3 (n) = o (log2 (n))
log (n!) = log (n * (n -1) * ... * 1) = logn + log (n - 1) + log (n - 2) + ... + log2 + log1 = o (nlogn)
Dans l'image suivante, nous pouvons voir clairement les notations.
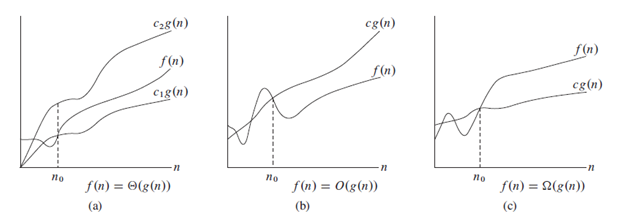
Remarque : il est convaincu d'utiliser O au lieu de Teta (scientifiquement incorrect).
Pour analyser les algorithmes récursifs, nous pouvons les analyser intuitivement en considérant un arbre et les opérations nécessaires sur chaque couche, et simplement les multiplier. Mais cela ne fonctionnera pas tout le temps.
Théorème de maître : dans l'image suivante, le théorème de maître est montré, que nous pouvons facilement utiliser pour analyser nos algorithmes récursifs. Cependant, nous devons être en mesure d'écrire l'équation récursive de l'algorithme récursif que nous voulons analyser.
