อัลกอริทึมเป็นขั้นตอนที่ประกอบด้วยชุดคำสั่ง จำกัด ซึ่งได้รับอินพุตจากชุดอินพุตที่เป็นไปได้บางชุดทำให้สามารถรับเอาต์พุตได้
Donald Knuth:“ วิทยาการคอมพิวเตอร์คือการศึกษาอัลกอริทึม ”
การเรียงลำดับการแทรกเป็นอัลกอริทึมการเรียงลำดับที่ง่ายซึ่งทำงานคล้ายกับวิธีที่คุณเรียงลำดับการเล่นไพ่ในมือของคุณ อาร์เรย์ถูกแบ่งออกเป็นส่วนที่เรียงลำดับและไม่เรียงลำดับ ค่าจากส่วนที่ไม่ได้เรียงลำดับจะถูกเลือกและวางไว้ที่ตำแหน่งที่ถูกต้องในส่วนที่เรียงลำดับ
หมายเหตุ : การค้นหาสถานที่ที่เหมาะสมขององค์ประกอบที่เลือกเป็นอัลกอริทึมอื่นเราต้องหาสถานที่ของมันโดยการเปรียบเทียบและเปลี่ยนไปจนกว่าจะหาสถานที่ที่ถูกต้อง ฉันสังเกตที่นี่เพราะฉันจำได้ว่าเป็นครั้งแรกที่ฉันได้เรียนรู้เกี่ยวกับอัลกอริทึมโดยเฉพาะอย่างยิ่งการเรียงลำดับหนึ่งฉันมักจะคิดระดับสูงและด้วยเหตุนี้ฉันจึงคิดว่าฉันไม่มีใจที่จะเข้าใจหรือแม้แต่การออกแบบอัลกอริทึม
ฉันถ่ายภาพต่อไปนี้ว่าอัลกอริทึมการแทรกทำงานจาก Wikipedia อย่างไร นอกจากนี้ยังมีเว็บไซต์อื่น ๆ อีกมากมายเช่น VisualGo ที่แสดงภาพอัลกอริทึมเหล่านี้และโครงสร้างข้อมูล
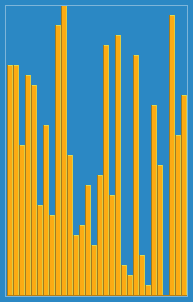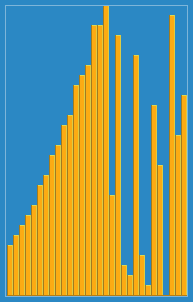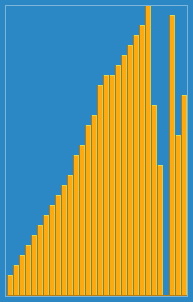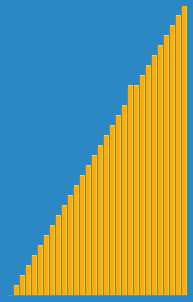
คุณสามารถค้นหาซอร์สโค้ดของอัลกอริทึมนี้ใน Python ได้ที่นี่ ความซับซ้อนของอัลกอริทึมนี้คือ O (n 2 ) เพราะประกอบด้วยลูปซ้อนกันสองตัว
อัลกอริทึมการเรียงลำดับนี้เป็นอัลกอริทึมการแบ่งและพิชิตซึ่งแบ่งอาร์เรย์ออกเป็นสองอาร์เรย์ครึ่งหนึ่งและหลังจากเรียงลำดับแยกกัน ตัวอย่างต่อไปนี้นำมาจาก Wikipedia
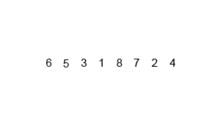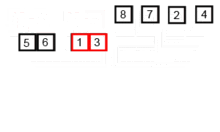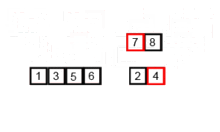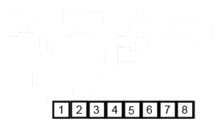
คุณสามารถค้นหาซอร์สโค้ดของอัลกอริทึมนี้ใน Python ได้ที่นี่ ความซับซ้อนของอัลกอริทึมนี้คือ O (nlogn) วิสัยทัศน์ของความซับซ้อนคือเพราะในแต่ละขั้นตอนของอัลกอริทึมนี้ทุกอาร์เรย์ที่มีความยาวของ n แบ่งออกเป็น 2 subarrays ดังนั้นเราจึงมีต้นไม้แห่งการปฏิบัติการที่มีความสูงของการเข้าสู่ระบบและเพราะในแต่ละระดับของต้นไม้
เพื่อให้เข้าใจว่าความซับซ้อนมีความสำคัญอย่างไรและมีความรู้สึกว่า O (Nlogn) เร็วกว่า O (N 2) ที่เร็วกว่า (N 2 ) ไฟล์อินพุตที่มีตัวเลขสุ่ม 1M ในโฟลเดอร์อินพุตถูกสร้างขึ้นจากนั้นป้อนไปยังอัลกอริทึม เพียงไปทดสอบพวกเขาและดูความแตกต่างของเวลาดำเนินการระหว่างพวกเขา
การวิเคราะห์เชิงซีมโทติคในการวิเคราะห์ทางคณิตศาสตร์การวิเคราะห์เชิงซีมโทติคหรือที่เรียกว่า asymptotics เป็นวิธีการอธิบายพฤติกรรมการ จำกัด ในการวิเคราะห์ความซับซ้อนของอัลกอริทึมเราอ้างถึงวิธีนี้เพื่อให้สามารถเปรียบเทียบอัลกอริทึมโดยทั่วไปโดยใช้สัญกรณ์ O โดยทั่วไป คุณสามารถดูตัวอย่างดังนี้:
n 2 + 5n + 10 = o (n 2 )
log3 (n) = o (log2 (n))
บันทึก (n!) = log (n * (n -1) * ... * 1) = logn + log (n - 1) + log (n - 2) + ... + log2 + log1 = o (nlogn)
ในภาพต่อไปนี้เราสามารถเห็นสัญลักษณ์ได้อย่างชัดเจน
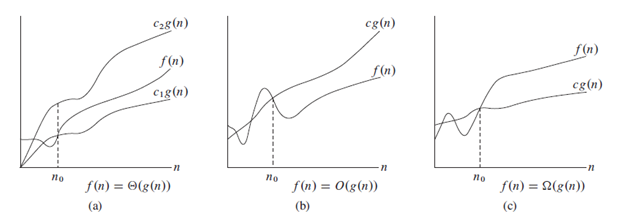
หมายเหตุ : มันเป็นความเชื่อมั่นที่จะใช้ o แทน teta (ไม่ถูกต้องทางวิทยาศาสตร์)
สำหรับการวิเคราะห์อัลกอริธึมแบบเรียกซ้ำเราสามารถวิเคราะห์ได้อย่างสังหรณ์ใจโดยพิจารณาจากต้นไม้และการดำเนินการที่จำเป็นในแต่ละชั้นและเพิ่มทวีคูณ แต่มันจะไม่ทำงานตลอดเวลา
ทฤษฎีบทหลัก : ในภาพต่อไปนี้ทฤษฎีบทมาสเตอร์จะปรากฏขึ้นซึ่งเราสามารถใช้เพื่อวิเคราะห์อัลกอริทึมแบบเรียกซ้ำของเราได้อย่างง่ายดาย อย่างไรก็ตามเราต้องสามารถเขียนสมการแบบเรียกซ้ำของอัลกอริทึมแบบเรียกซ้ำที่เราต้องการวิเคราะห์
