الخوارزمية هي إجراء يتكون من مجموعة محدودة من التعليمات التي ، بالنظر إلى المدخلات من مجموعة من المدخلات المحتملة ، تتيح الحصول على مخرجات.
دونالد نوث: " علوم الكمبيوتر هي دراسة الخوارزميات".
يعد نوع الإدراج خوارزمية فرز بسيطة تعمل بشكل مشابه للطريقة التي تقوم بها بفرز أوراق اللعب بين يديك. يتم تقسيم المصفوفة فعليًا إلى جزء مصنّف غير مصنف. يتم اختيار القيم من الجزء غير المصقول ووضعها في الموضع الصحيح في الجزء المرتبة.
ملاحظة : العثور على المكان المناسب للعنصر الذي تم اختياره هو خوارزمية أخرى ، علينا أن نجد مكانها من خلال المقارنة والتحول حتى العثور على مكانها الصحيح. لقد لاحظت ذلك هنا لأنني أتذكر ، بينما تعلمت لأول مرة الخوارزميات ، وخاصة فرز واحدة ، كنت أفكر دائمًا في المستوى العالي ، وبسبب ذلك ، كنت أفكر أنه ليس لدي عقل لفهم أو حتى خوارزميات التصميم.
التقطت الصورة التالية لكيفية عمل خوارزمية الإدراج من ويكيبيديا. أيضًا ، هناك العديد من مواقع الويب الأخرى مثل VisualGo التي تصور هذه الخوارزميات وأيضًا هياكل البيانات.
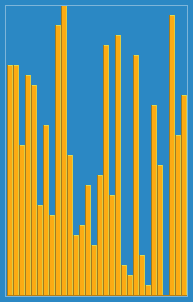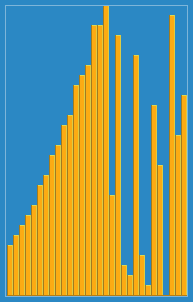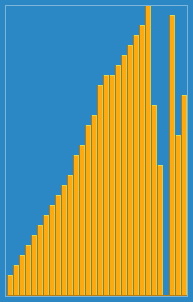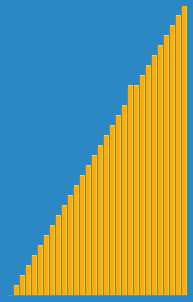
يمكنك العثور على الكود المصدري لهذه الخوارزمية في بيثون هنا. تعقيد هذه الخوارزمية هو O (n 2 ) لأنها تتكون من حلقتين متداخلتين.
خوارزمية الفرز هذه هي خوارزمية الفجوة والقهر ، والتي تقسم صفيف إلى صفيفتين نصف ، وبعد فرزها بشكل منفصل ، يدمجهم لبناء الصفيف بأكمله مرة أخرى. المثال التالي مأخوذ من ويكيبيديا.
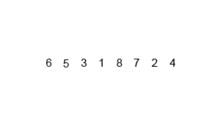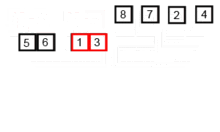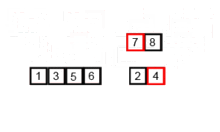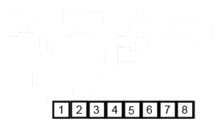
يمكنك العثور على الكود المصدري لهذه الخوارزمية في بيثون هنا. تعقيد هذه الخوارزمية هو o (nlogn). تتمثل رؤية التعقيد في أنه في كل خطوة من هذه الخوارزمية ، يتم تقسيم كل صفيف بطول N إلى 2 طوائف فرعية ولذا لدينا شجرة من العمليات ذات ارتفاع logn ، وأيضًا لأنه في كل مستوى من الشجرة ، يتعين علينا دمج اثنين من اللغات الفرعية التي تتطلب حلقة تكرر على عناصر n بحيث تكون تعقيد الخوارزمية (NX logn).
لفهم مدى أهمية التعقيد وأيضًا أن يكون لديك شعور حول مدى أسرع O (nlogn) من O (n 2 ) ، يتم إنشاء ملف إدخال بأرقام عشوائية 1M في مجلد الإدخال ، ثم يتم تغذية الخوارزميات. فقط اذهب واختبرهم وشاهد فرق وقت التنفيذ بينهما.
يعد التحليل المقارب في التحليل الرياضي ، والتحليل المقارب ، والمعروف أيضًا باسم عدم المقارب ، وسيلة لوصف سلوك الحد. في تحليل تعقيد الخوارزميات ، نشير إلى هذه الطريقة لتكون قادرة على مقارنة الخوارزميات عمومًا ، باستخدام تدوين O بشكل عام. يمكنك رؤية بعض الأمثلة على النحو التالي:
n 2 + 5n + 10 = o (n 2 )
log3 (n) = o (log2 (n))
log (n!) = log (n * (n -1) * ... * 1) = logn + log (n - 1) + log (n - 2) + ... + log2 + log1 = o (nlogn)
في الصورة التالية ، يمكننا أن نرى الرموز بوضوح.
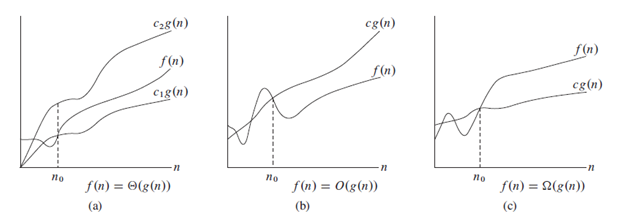
ملاحظة : من القبول استخدام O بدلاً من Teta (غير صحيح علميًا).
لتحليل الخوارزميات العودية ، يمكننا تحليلها بشكل حدسي من خلال النظر في شجرة والعمليات اللازمة على كل طبقة ، وضربها فقط. ولكن ، لن يعمل طوال الوقت.
النظرية الرئيسية : في الصورة التالية ، يتم عرض نظرية Master ، والتي يمكننا استخدامها بسهولة لتحليل خوارزمياتنا المتكررة. ومع ذلك ، يجب أن نكون قادرين على كتابة المعادلة العودية للخوارزمية العودية التي نريد تحليلها.
