算法是由一组有限的指令组成的过程,该指令从某些可能的输入中给出了输入,使得能够获得输出。
唐纳德·诺斯(Donald Knuth):“计算机科学是算法的研究。 ”
插入排序是一种简单的排序算法,其工作方式类似于您手中的扑克牌的方式。该数组实际上分为分类和未分类的部分。从分类部件中挑选未分类零件的值并将其放置在排序部分的正确位置。
注意:找到采摘元件的正确位置是另一种算法,我们必须通过比较和转移来找到其位置,直到找到正确的位置。我在这里注意到这一点,因为我记得第一次了解算法,尤其是对算法进行分类,总是想到很高的水平,因此,我认为我没有理解甚至设计算法的思想。
我拍摄了以下图像,介绍了Wikipedia插入算法的工作方式。此外,还有许多其他网站(例如VisualGo)可视化这些算法和数据结构。
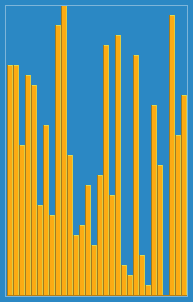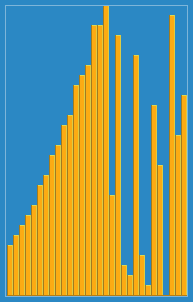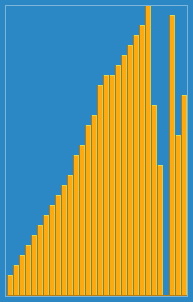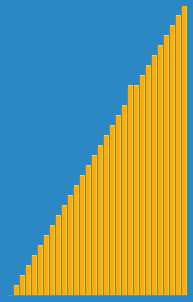
您可以在此处的Python中找到此算法的源代码。该算法的复杂性为O(n 2 ),因为它由两个嵌套环组成。
该排序算法是一种分裂和争议算法,该算法将数组分为两个半数组,然后对它们进行分类后,将它们合并以再次构建整个数组。以下示例取自Wikipedia。
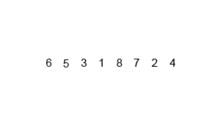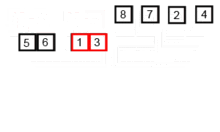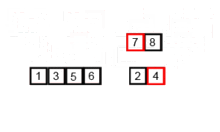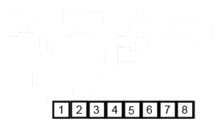
您可以在此处的Python中找到此算法的源代码。该算法的复杂性为O(nlogn)。复杂性的视野是,因为在该算法的每个步骤中,每个阵列的长度都分为两个子阵列,因此我们有一棵具有LOGN高度的操作树,而且因为在树的每个级别中,我们必须合并两个子阵列,需要在n元素上进行n元素的循环,以便algorithm的复杂性(nx logn)。
要了解复杂性的重要性,并且对O(n2)的速度( n2 )的速度快,也会生成一个输入文件夹中的输入文件,然后将其输入到算法中。只需去测试它们,看看它们之间的执行时间差即可。
数学分析中的渐近分析,渐近分析(也称为渐近分析)是一种描述限制行为的方法。在分析算法复杂性时,我们将此方法通常使用o符号通常比较算法。您可以看到一些示例如下:
n 2 + 5n + 10 = o(n 2 )
log3(n)= O(log2(n))
log(n!)= log(n *(n -1) * ... * 1)= logn + log(n -1) + log(n -2) + ... + ... + log2 + log1 = o(nlogn)
在下面的图像中,我们可以清楚地看到符号。
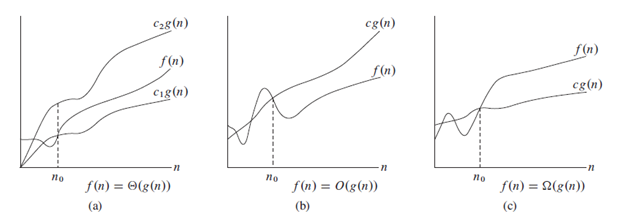
注意:使用O而不是TETA(科学上不正确)是对话。
为了分析递归算法,我们可以通过考虑一棵树和每一层所需的操作,然后将它们乘以它们来直观地分析它们。但是,它不会一直工作。
主定理:在下面的图像中,显示了主定理,我们可以轻松地用于分析递归算法。但是,我们必须能够编写要分析的递归算法的递归方程。
