Алгоритм - это процедура, которая состоит из конечного набора инструкций, которые, предоставляя входные данные из некоторого набора возможных входов, позволяет получить выход.
Дональд Кнут: « Информатика - это изучение алгоритмов».
Вставка - это простой алгоритм сортировки, который работает аналогично тому, как вы сортируете играющие карты в ваших руках. Массив практически разделен на отсортированную и несортированную часть. Значения из несортированной части выбираются и расположены в правильном положении в отсортированной части.
Примечание . Поиск подходящего места выбранного элемента является еще одним алгоритмом, мы должны найти его место, сравнивая и переключившись до поиска правильного места. Я отметил это здесь, потому что я помню, когда впервые узнал об алгоритмах, особенно сортируя его, всегда я думал так высокий уровень, и из -за этого я думал, что у меня нет ума, чтобы понять или даже алгоритмы дизайна.
Я сделал следующее изображение того, как работает алгоритм вставки из Википедии. Кроме того, есть много других веб -сайтов, таких как Visualgo, которые визуализируют эти алгоритмы, а также структуры данных.
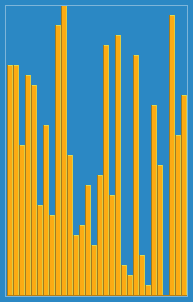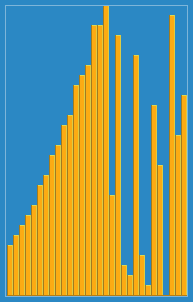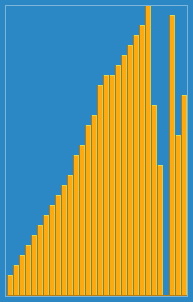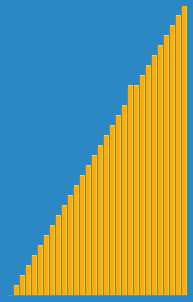
Вы можете найти исходный код этого алгоритма в Python здесь. Сложность этого алгоритма - O (N 2 ), потому что он состоит из двух вложенных петель.
Этот алгоритм сортировки представляет собой алгоритм разделения и контроля, который разделяет массив на два половину массива, и после сортировки их отдельно объединяет их, чтобы снова построить весь массив. Следующий пример взят из Википедии.
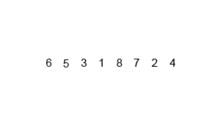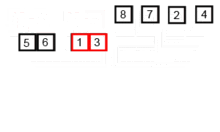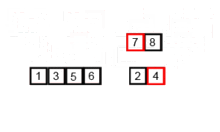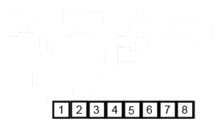
Вы можете найти исходный код этого алгоритма в Python здесь. Сложность этого алгоритма - o (nlogn). Видение сложности состоит в том, что, поскольку на каждом этапе этого алгоритма каждый массив с длиной n делится на 2 субарри, и поэтому мы имеем дерево операций с высотой logn, а также потому, что на каждом уровне дерева мы должны объединить два субрада, требующие цикла, итерационного на n -элементах, поэтому сложности алгоритма (NX logn).
Чтобы понять, насколько важна сложность, а также иметь ощущение, насколько быстрее o (nlogn), чем O (n 2 ), генерируется входной файл с 1 млн. Случайных чисел в входной папке, а затем подается в алгоритмы. Просто пройдите и протестируйте их и увидите разницу во времени выполнения между ними.
Асимптотический анализ в математическом анализе, асимптотический анализ, также известный как асимптотики, является методом описания ограничивающего поведения. При анализе сложности алгоритмов мы ссылаемся на этот метод, чтобы иметь возможность сравнивать алгоритмы, как правило, используя o обозначения в целом. Вы можете увидеть какой -то пример следующим образом:
n 2 + 5n + 10 = O (n 2 )
log3 (n) = o (log2 (n))
log (n!) = log (n * (n -1) * ... * 1) = logn + log (n - 1) + log (n - 2) + ... + log2 + log1 = o (nlogn)
На следующем изображении мы можем ясно увидеть нотации.
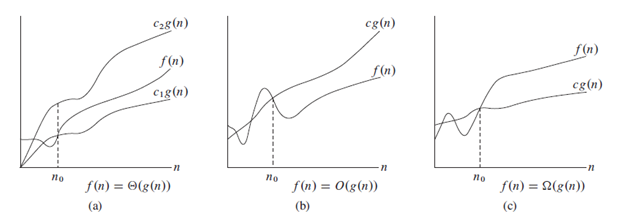
Примечание : это конвенция для использования o вместо TETA (научно неверно).
Для анализа рекурсивных алгоритмов мы можем интуитивно проанализировать их, рассматривая дерево и операции, необходимые на каждом уровне, и просто умножить их. Но это не будет работать все время.
Мастер -теорема : На следующем изображении показана мастер -теорема, которую мы можем легко использовать для анализа наших рекурсивных алгоритмов. Тем не менее, мы должны быть в состоянии написать рекурсивное уравнение рекурсивного алгоритма, который мы хотим проанализировать.
