pyoptim下载pyoptim源代码下载

Pyoptim：用于优化和矩阵操作的Python软件包

一个python软件包，该软件包在十种无约束的优化算法附近集成，其中包括2D/3D可视化的比较分析，并结合了矩阵操作。

该项目是Ensias的数值分析与优化课程的一个组成部分，Mohammed v University源于M. Naoum教授的建议，即创建一个python包装，封装了实验室会议期间实践的算法。它重点介绍了大约十种不受限制的优化算法，提供2D和3D可视化，从而可以在计算效率和准确性方面进行性能比较。此外，该项目涵盖了矩阵操作，例如反转，分解和求解线性系统，所有这些都集成在包含实验室衍生算法的软件包中。

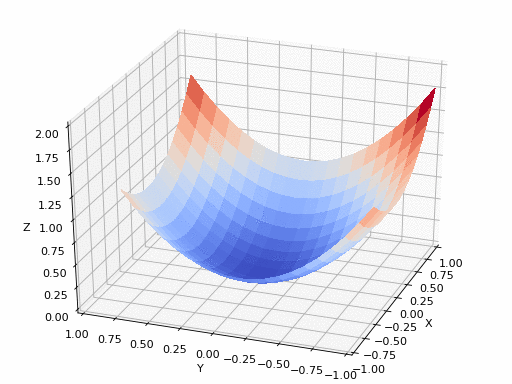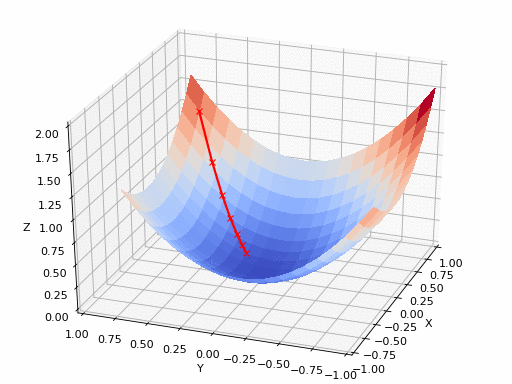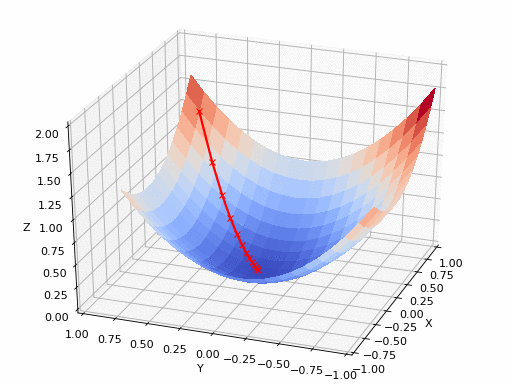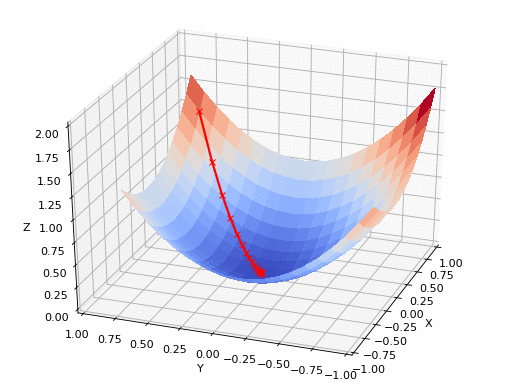
GIF来源：https：//www.nsf.gov/news/mmg/mmg/mmg_disp.jsp?med_id = 78950&from=]

该项目的每个部分都是示例代码，该代码显示了如何执行以下操作：

实现单变量优化算法，encompassing fixed_step，Accelerated_step，Enternive_search，dichotomous_search，Interval_halving，fibonacci，fibonacci，golden_section，golden_section，armijo_backward和armijo_forward。
掺入各种单变量优化算法，包括梯度下降，梯度共轭，牛顿，Quasi_newton_dfp，随机梯度下降。
2D，轮廓和3D格式中所有算法的每个迭代步骤的可视化。
进行比较分析，重点是其运行时和准确性指标。
矩阵操作的实施，例如反转（例如，高斯 - 约旦），分解（例如，LU，Choleski）和线性系统的解决方案（例如，高斯 - 约旦，LU，Choleski）。
入门

安装此Python软件包：

 pip install pyoptim

运行此演示笔记本

文档和比较分析

单变量优化算法
- 导入库
- Objectif函数
- 参数初始化
- 固定步骤
- 加速步骤
- 详尽的搜索
- 二分法搜索
- 间隔减半
- 斐波那契
- Golden_Section
- Armijo_backward
- Armijo_forward
- 比较分析
多变量优化算法
- 导入库
- Objectif函数
- 参数初始化
- 梯度下降
- 梯度共轭
- 牛顿
- 准牛顿DFP
- 随机梯度下降
- BLS的随机梯度下降
- 比较分析
矩阵逆
- 导入库
- 测试矩阵
- 高斯·乔丹
- 矩阵逆
- 矩阵逆
基质分解
- 导入库
- 测试矩阵
- 鲁
- Choleski
解决线性系统
- 导入库
- 测试矩阵
- 高斯·乔丹
- 鲁
- Choleski

单变量优化算法

导入库

 import pyoptim . my_scipy . onevar_optimize . minimize as soom
import pyoptim . my_plot . onevar . _2D as po2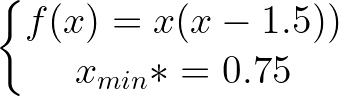

Objectif函数

 def f ( x ):
    return x * ( x - 1.5 )   # analytically, argmin(f) = 0.75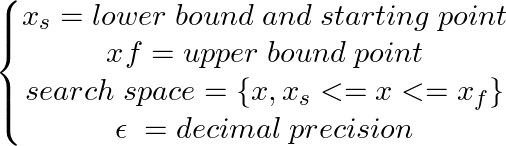

参数初始化

 xs = - 10
xf = 10
epsilon = 1.e-2

固定步骤

 print ( 'x* =' , soom . fixed_step ( f , xs , epsilon ))
po2 . fixed_step ( f , xs , epsilon )

 x* = 0.75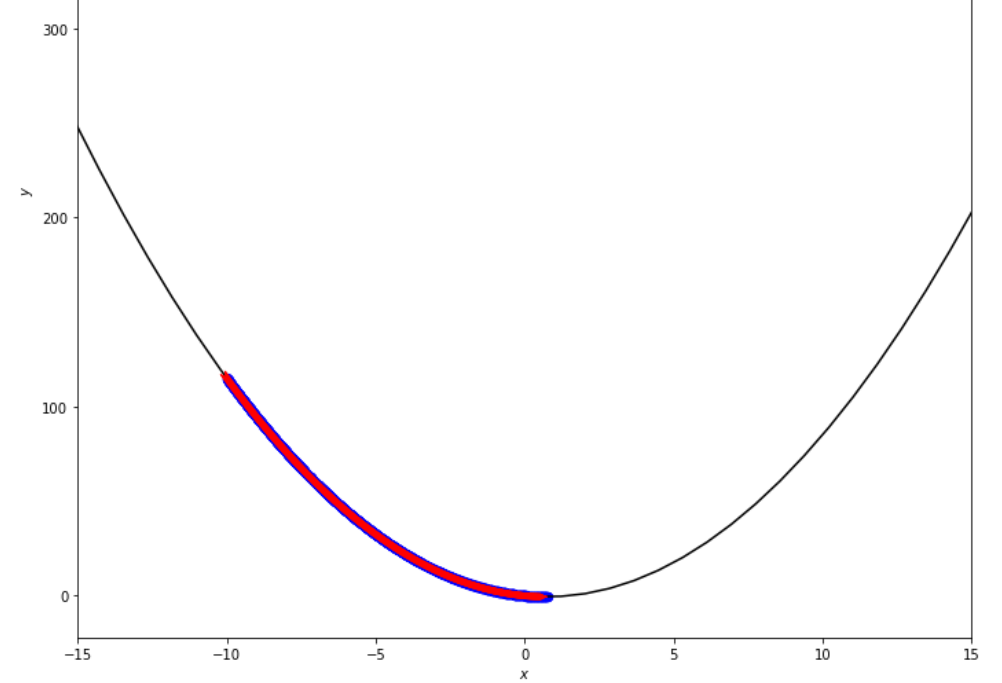

达到最小值之前，固定步骤算法采取的步骤顺序

加速步骤

 print ( 'x* =' , soom . accelerated_step ( f , xs , epsilon ))
po2 . accelerated_step ( f , xs , epsilon )

 x* = 0.86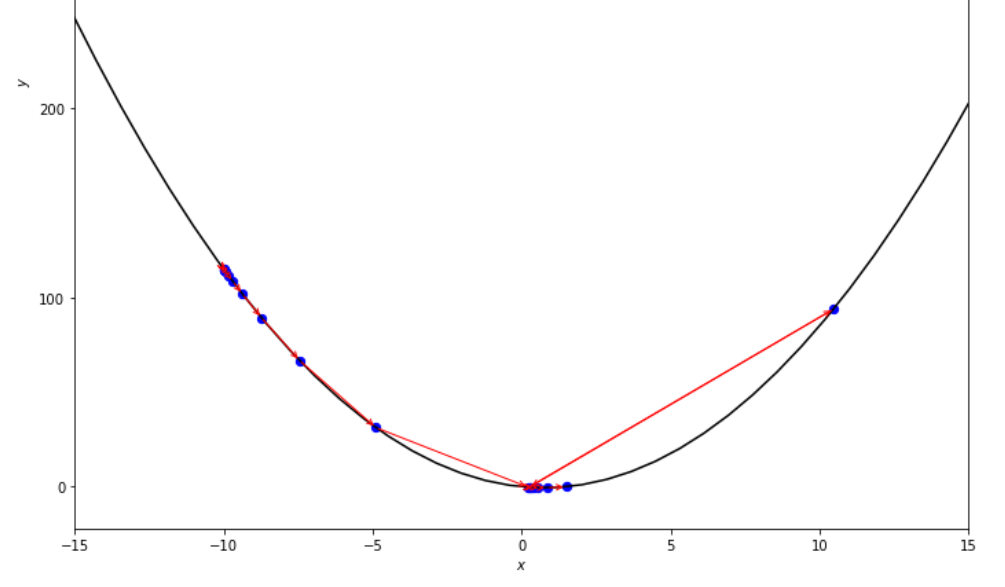

在达到最小值之前，加速步骤算法采取的步骤顺序

详尽的搜索

 print ( 'x* =' , soom . exhaustive_search ( f , xs , xf , epsilon ))
po2 . exhaustive_search ( f , xs , xf , epsilon )

 x* = 0.75

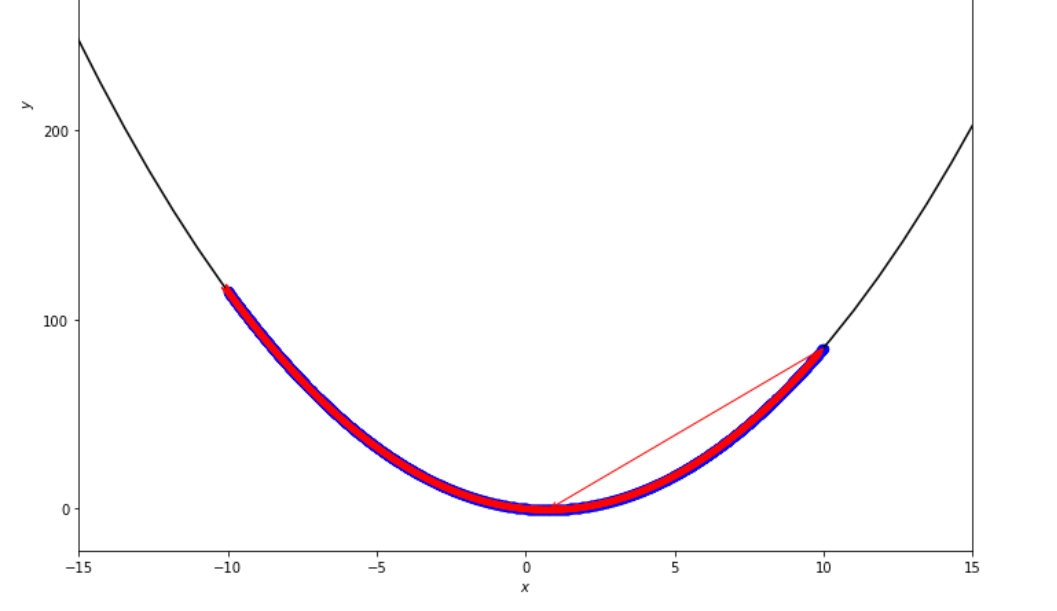
到达最小值之前，详尽的搜索算法采取的步骤顺序

二分法搜索

 mini_delta = 1.e-3
print ( 'x* =' , soom . dichotomous_search ( f , xs , xf , epsilon , mini_delta ))
po2 . dichotomous_search ( f , xs , xf , epsilon , mini_delta )

 x* = 0.7494742431640624

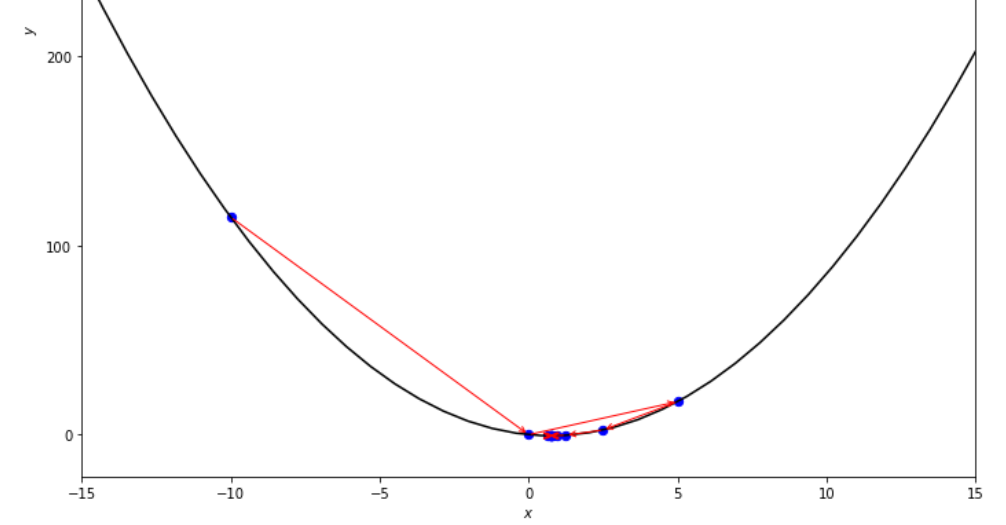
达到最小值之前，二分法搜索算法采取的步骤顺序

间隔减半

 print ( 'x* =' , soom . interval_halving ( f , xs , xf , epsilon ))
po2 . interval_halving ( f , xs , xf , epsilon )

 x* = 0.75

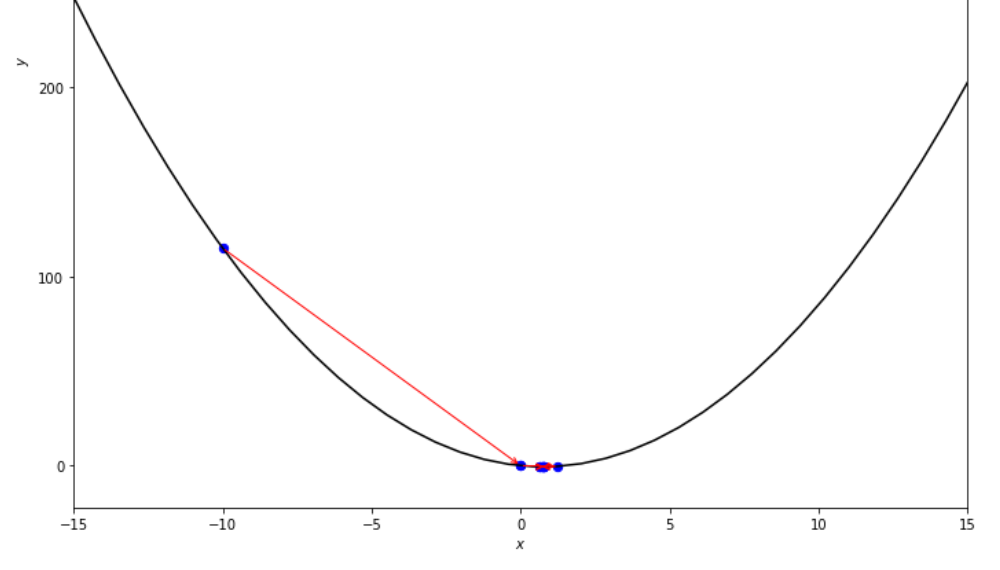
在达到最小值之前，间隔将算法减半的步骤序列。

斐波那契

 n = 15
print ( 'x* =' , soom . fibonacci ( f , xs , xf , n )) 
po2 . fibonacci ( f , xs , xf , n )

 x* = 0.76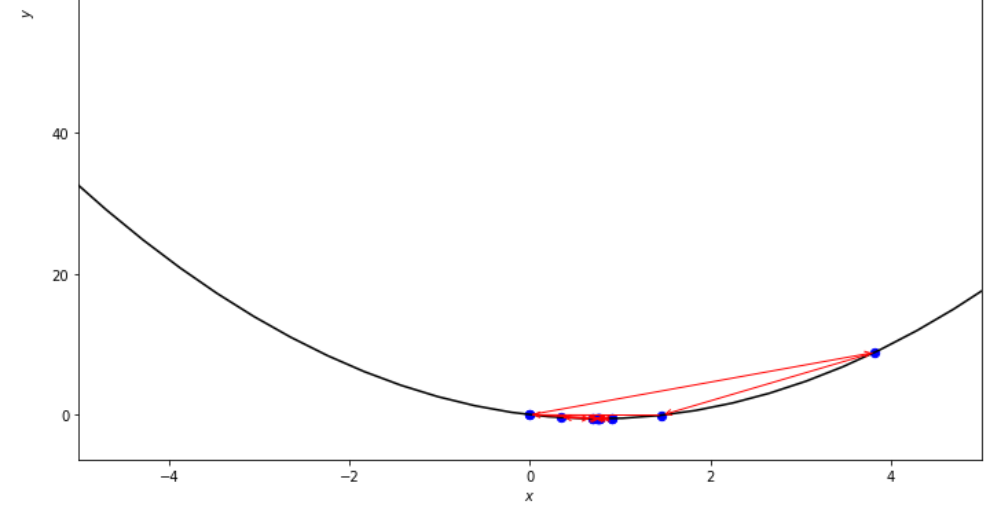

在达到最小值之前，斐波那契算法采取的步骤顺序。

黄金部分

 print ( 'x* =' , soom . golden_section ( f , xs , xf , epsilon ))
po2 . golden_section ( f , xs , xf , epsilon )

 x* = 0.75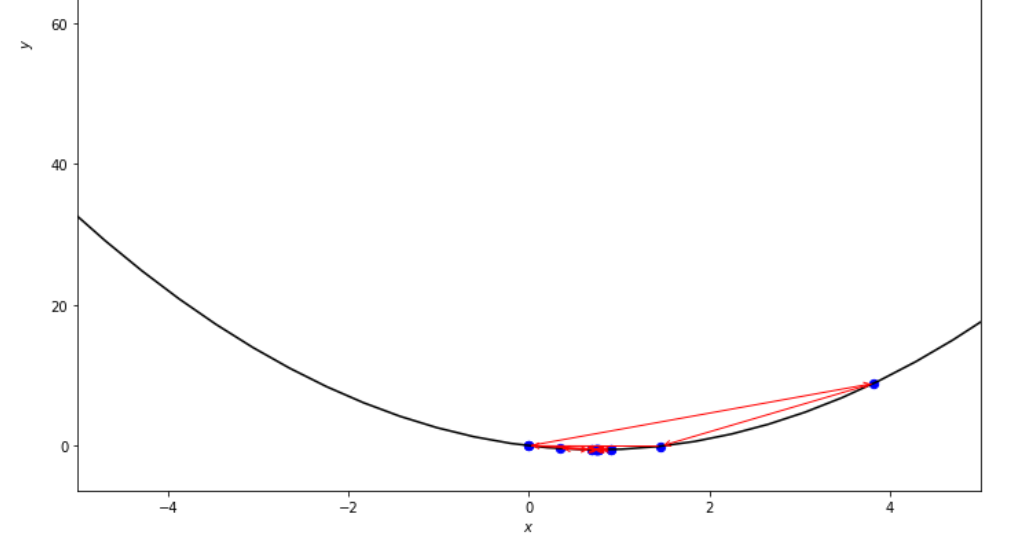

达到最小值之前，黄金部分算法采取的步骤顺序

Armijo向后

 ŋ = 2
xs = 100
print ( 'x* =' , soom . armijo_backward ( f , xs , ŋ , epsilon ))
po2 . armijo_backward ( f , xs , ŋ , epsilon )

 x* = 0.78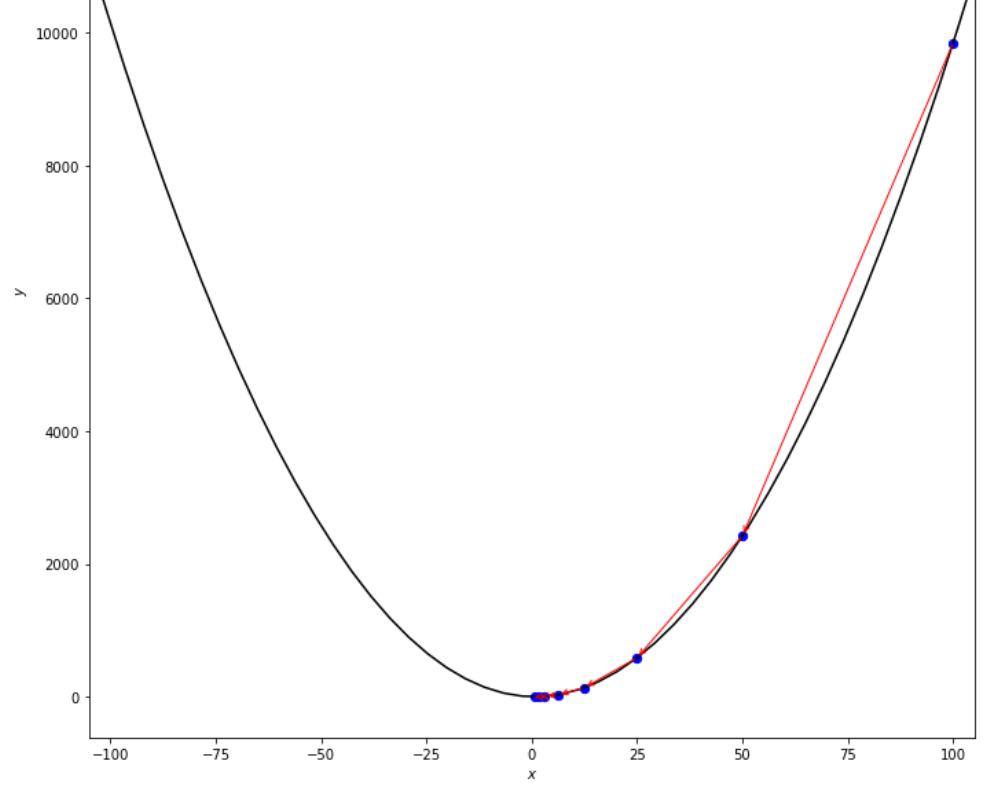

在达到最小值之前，Armijo向后算法采取的步骤顺序

Armijo前锋

 xs = 0.1
epsilon = 0.5
ŋ = 2
print ( 'x* =' , soom . armijo_forward ( f , xs , ŋ , epsilon ))
po2 . armijo_forward ( f , xs , ŋ , epsilon )

 x* = 0.8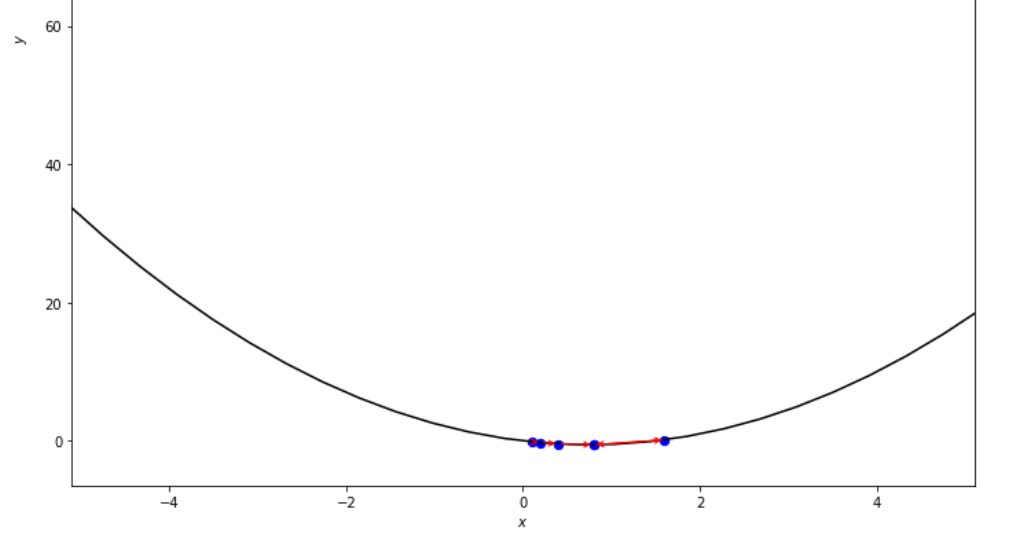

在达到最小值之前，Armijo前进算法采取的步骤顺序

比较分析

 po2 . compare_all_time ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 )

运行时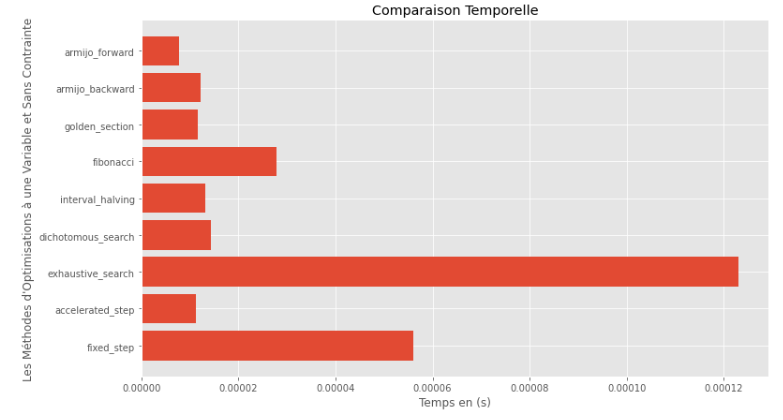

 po2 . compare_all_precision ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 )

真实和计算最小值之间的差距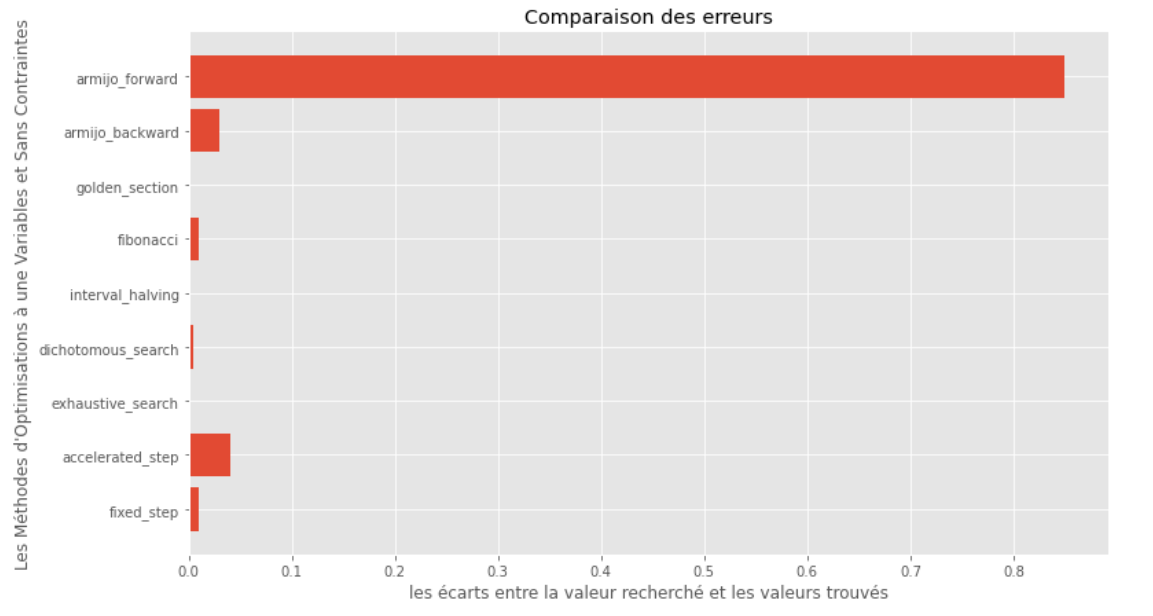

从运行时和精度图可以推断出，在该凸单动函数评估的算法中，金段方法作为最佳选择而出现，提供了高精度和尤其是较低的运行时的融合。

多变量优化算法

导入库

 import pyoptim . my_plot . multivar . _3D as pm3
import pyoptim . my_plot . multivar . contour2D as pmc

Objectif函数

 def h ( x ):
    return x [ 0 ] - x [ 1 ] + 2 * ( x [ 0 ] ** 2 ) + 2 * x [ 1 ] * x [ 0 ] + x [ 1 ] ** 2
# analytically, argmin(f) = [-1, 1.5]

分类解决方案

参数初始化

 X = [ 1000 , 897 ]
alpha = 1.e-2
tol = 1.e-2

梯度下降

 pmc . gradient_descent ( h , X , tol , alpha )
pm3 . gradient_descent ( h , X , tol , alpha )

 Y* =  [-1.01  1.51]

达到最小值之前，梯度下降算法采取的步骤顺序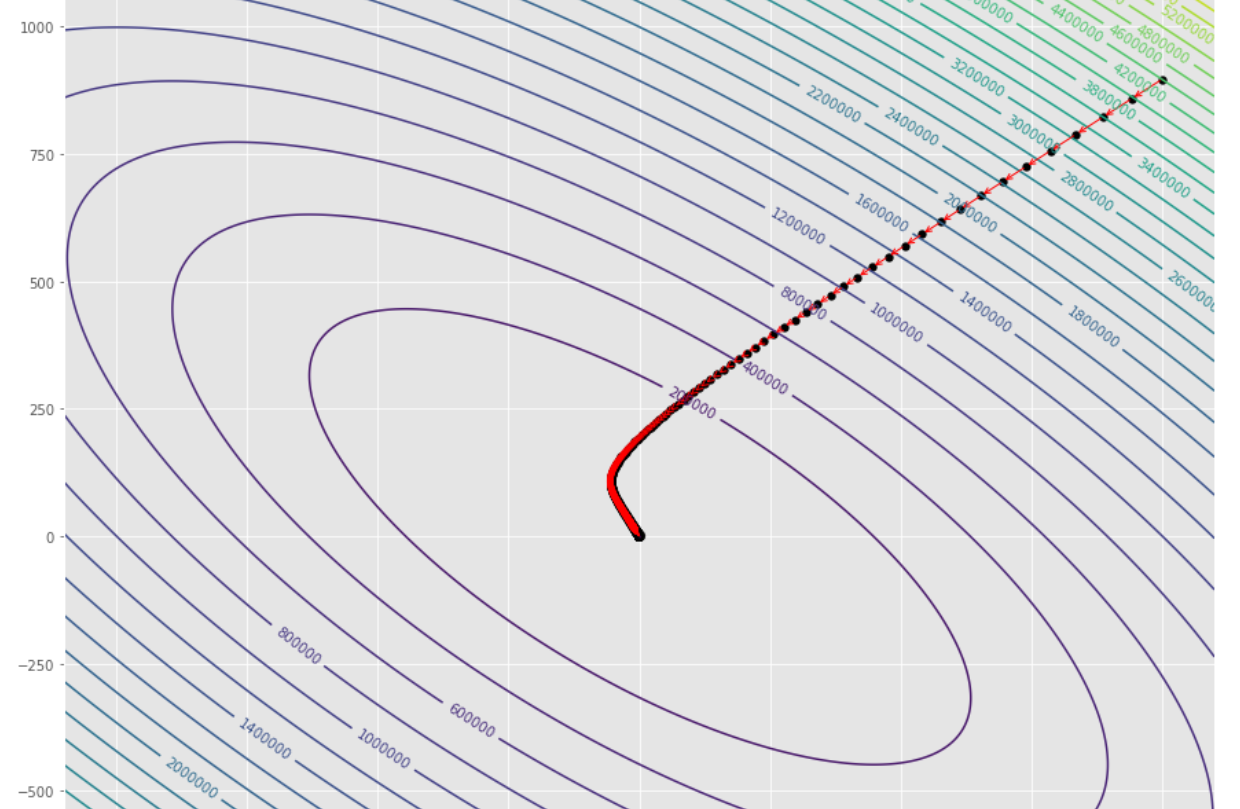

轮廓图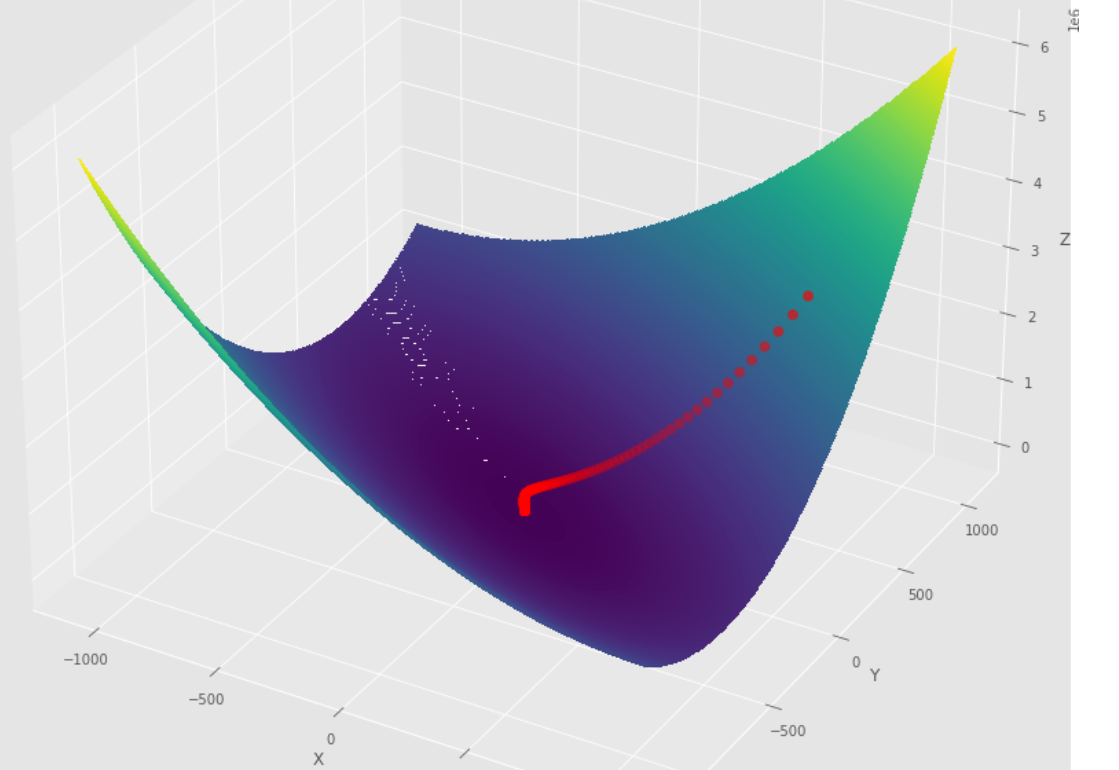

3D图

梯度共轭

 pmc . gradient_conjugate ( h , X , tol )
pm3 . gradient_conjugate ( h , X , tol )

 Y* =  [-107.38  172.18]

达到最小值之前，梯度共轭算法采取的步骤顺序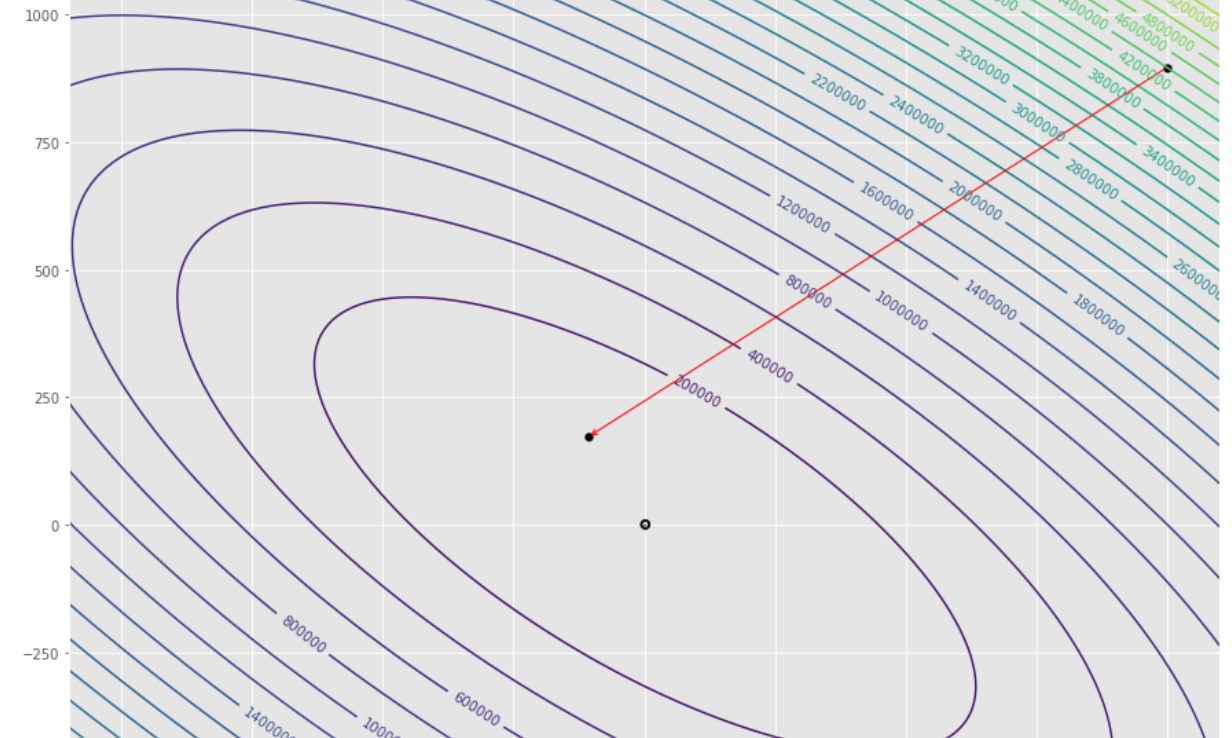

轮廓图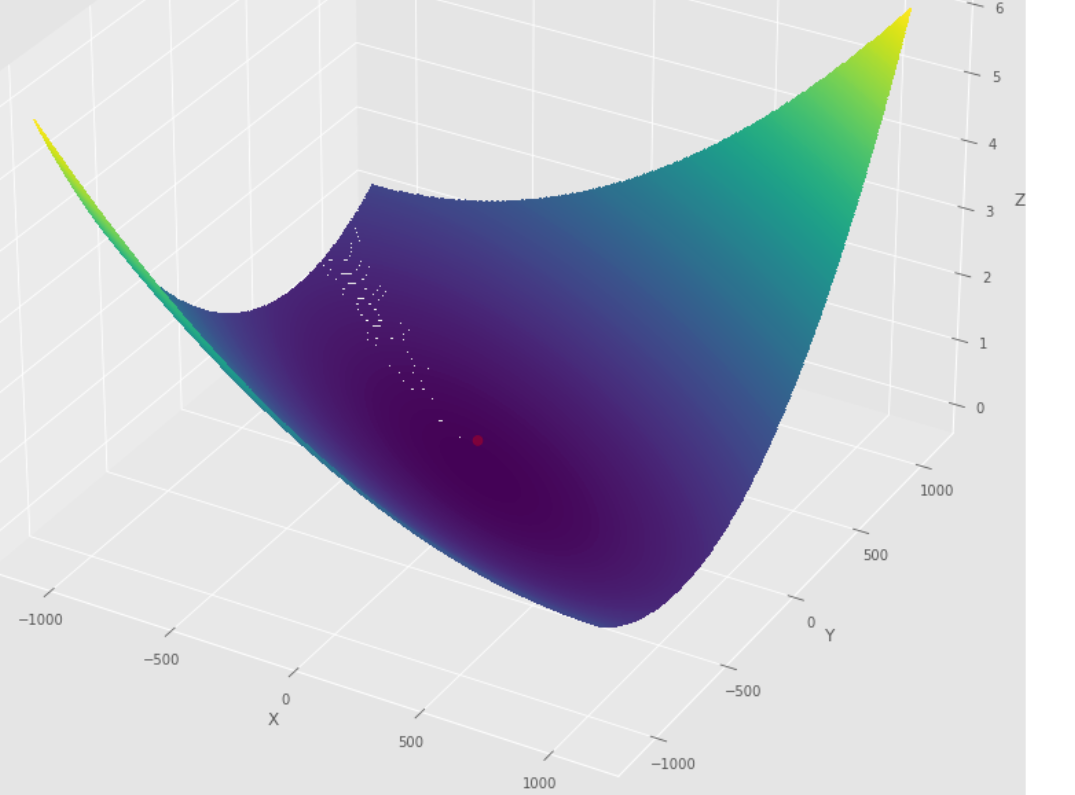

3D图

牛顿

 pmc . newton ( h , X , tol )
pm3 . newton ( h , X , tol )

 Y* =  [-1.   1.5]

达到最小值之前，牛顿算法采取的步骤顺序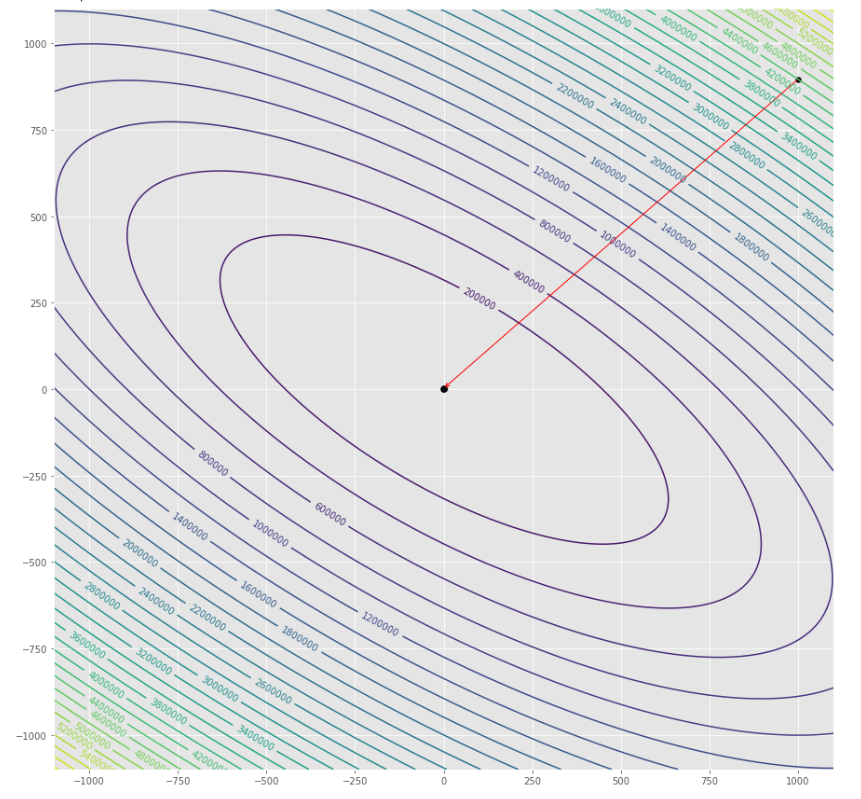

轮廓图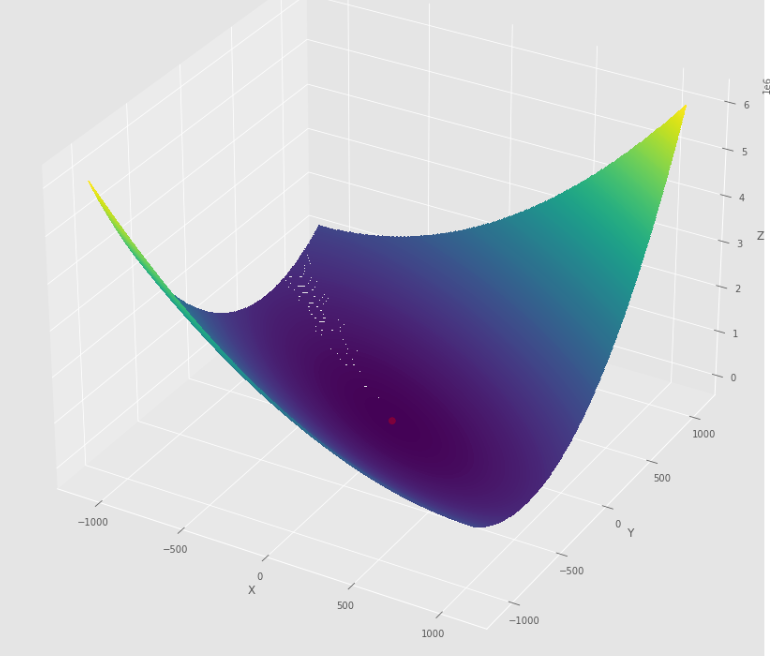

3D图

准牛顿DFP

 pmc . quasi_newton_dfp ( h , X , tol )
pm3 . quasi_newton_dfp ( h , X , tol )

 Y* =  [-1.   1.5]

准牛顿DFP算法采取的步骤顺序，然后达到最低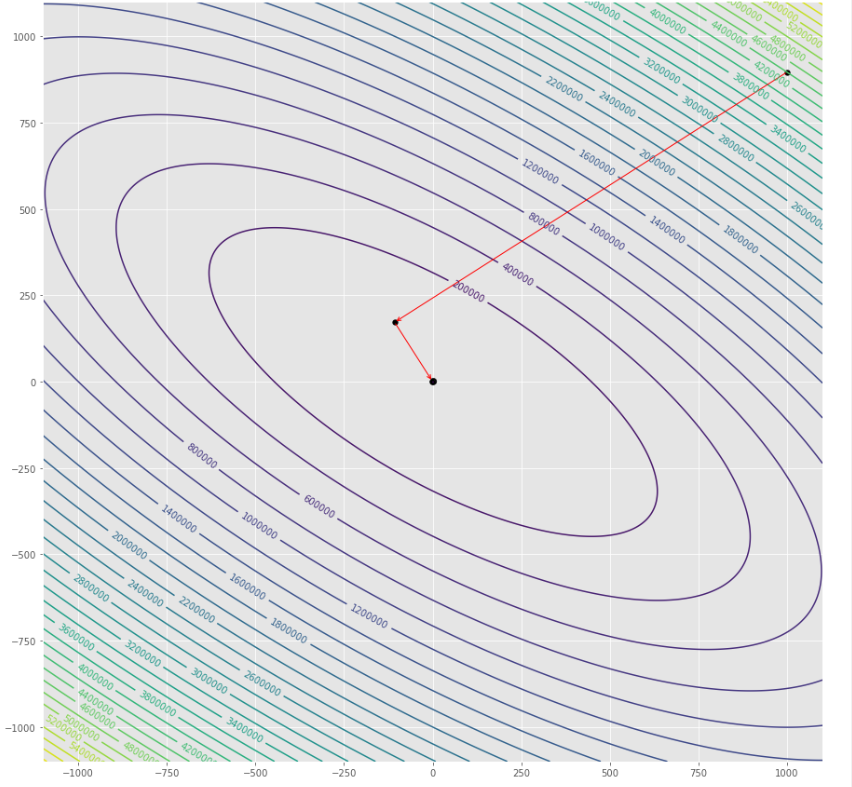

轮廓图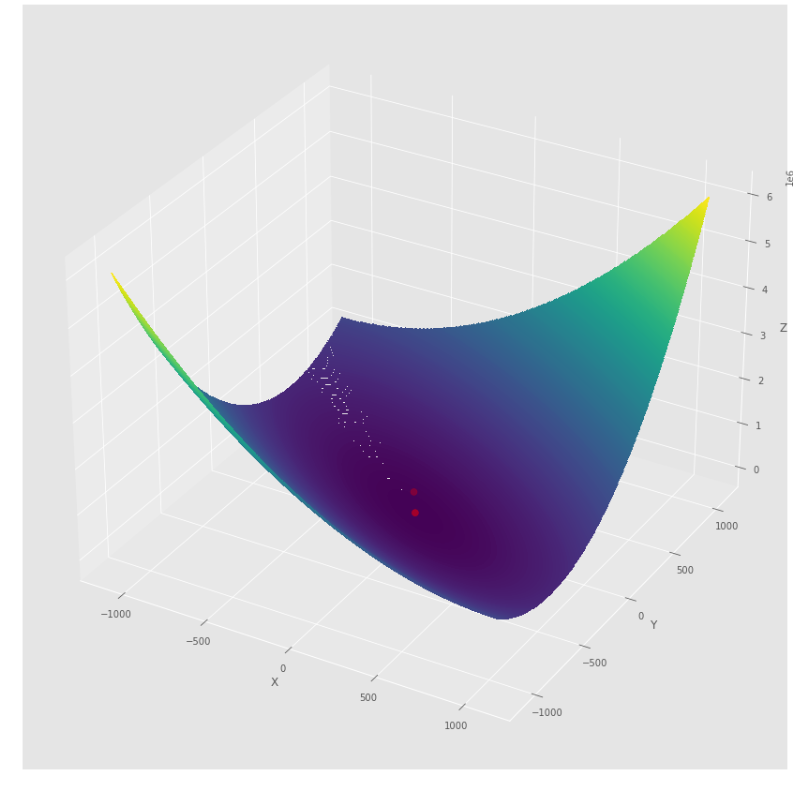

3D图

随机梯度下降

 pmc . sgd ( h , X , tol , alpha )
pm3 . sgd ( h , X , tol , alpha )

 Y* =  [-1.01  1.52]

在达到最小值之前，由随机梯度下降算法采取的步骤顺序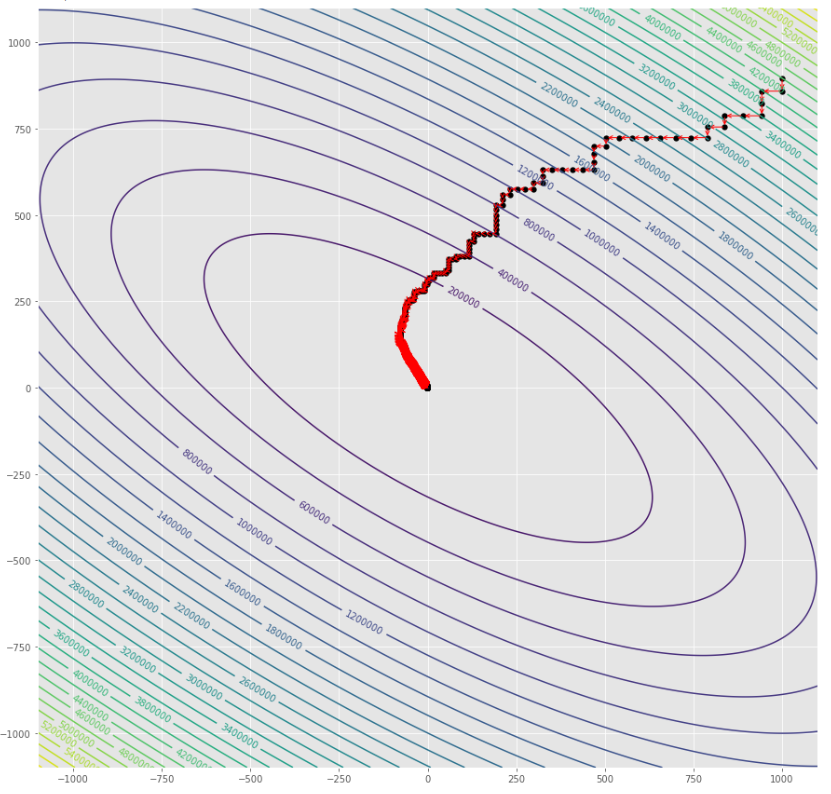

轮廓图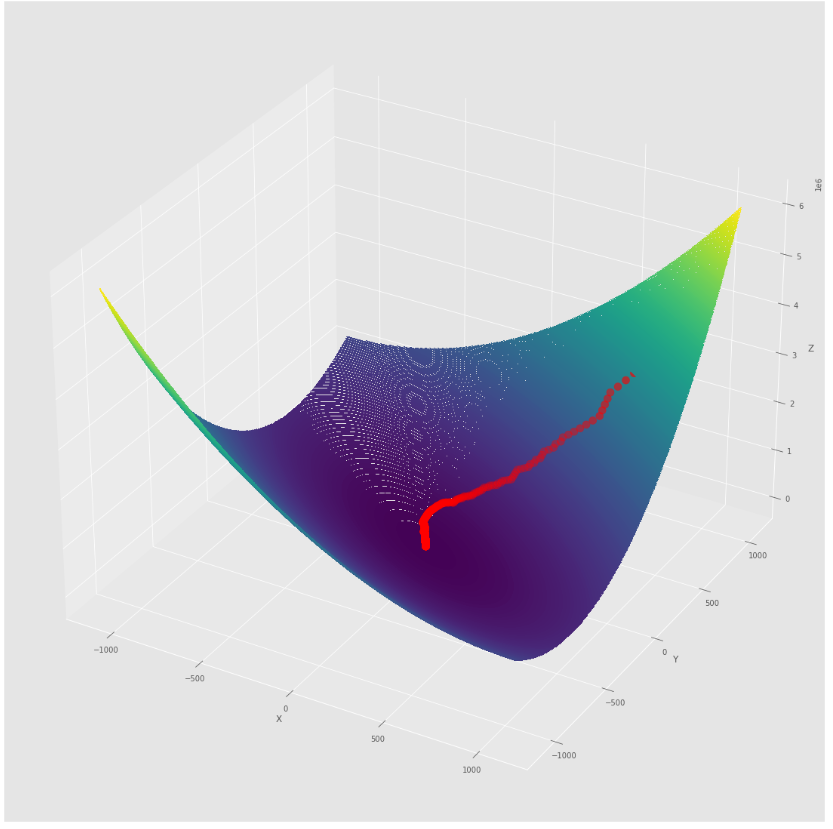

3D图

BLS的随机梯度下降

 alpha = 100 #it must be high because of BLS
c = 2
pmc . sgd_with_bls ( h , X , tol , alpha , c ) 
pm3 . sgd_with_bls ( h , X , tol , alpha , c )

 Y* =  [-1.   1.5]

在达到最小值之前，由随机梯度下降采取的步骤顺序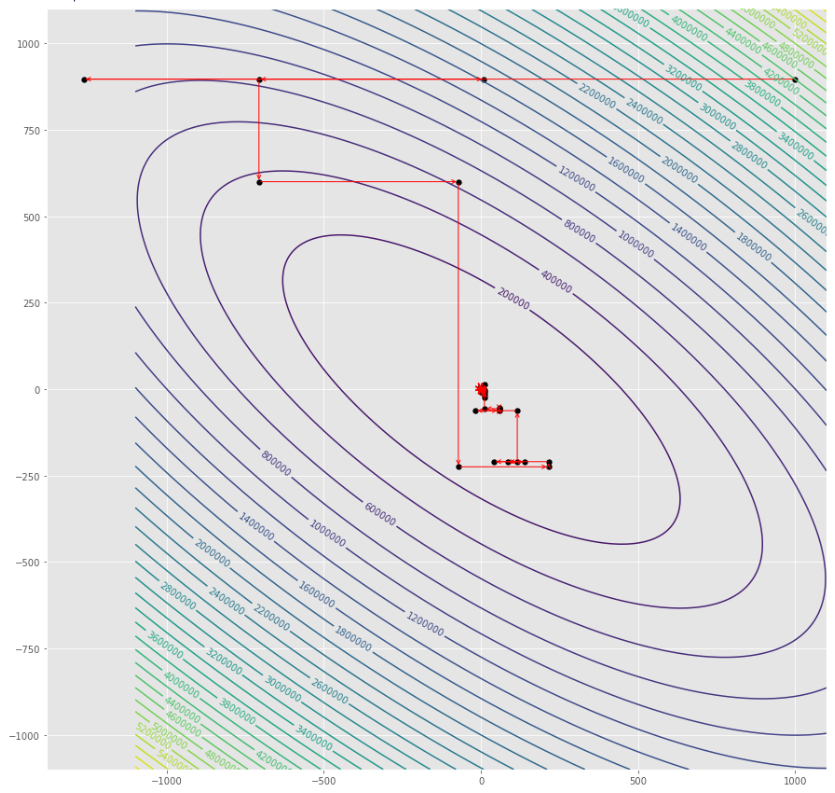

轮廓图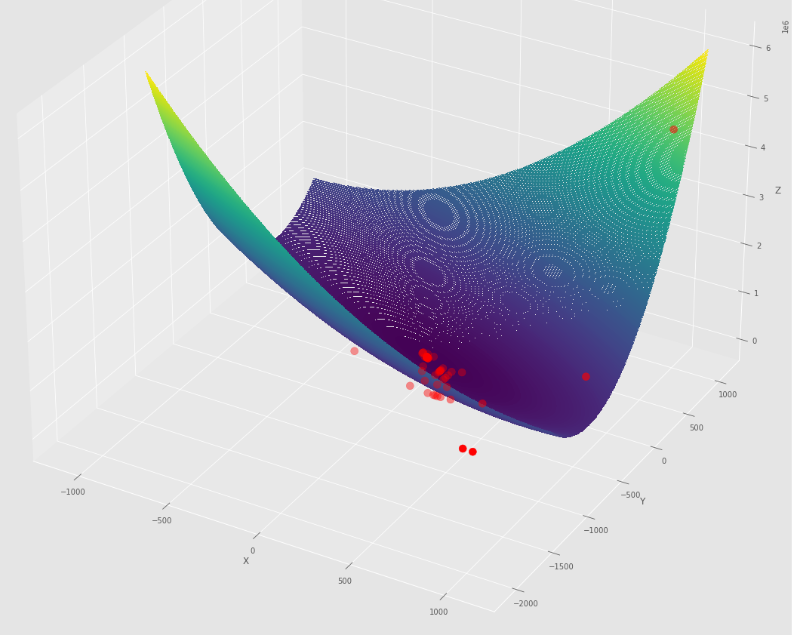

3D图

比较分析

 pm3 . compare_all_time ( h , X , 1.e-2 , 1.e-1 , 100 , 2 )

运行时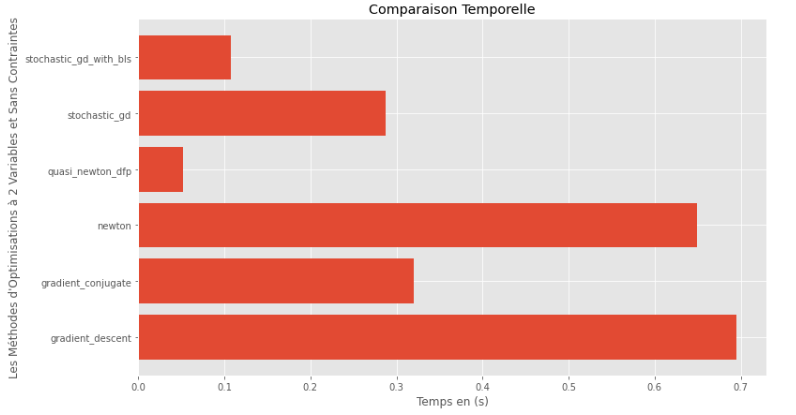

 pm3 . compare_all_precision ( h , X , 1.e-2 , 1.e-1 , 100 , 2 )

真实和计算最小值之间的差距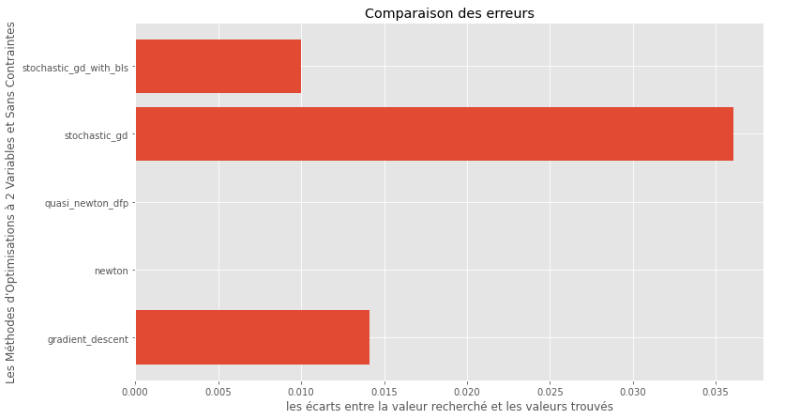

从运行时和精度图可以推断出，在该凸多变量函数评估的算法中，准牛顿DFP方法作为最佳选择而出现，提供了高精度和尤其是低运行时的融合。

矩阵逆

导入库

 import pyoptim . my_numpy . inverse as npi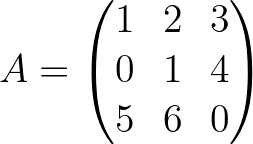

测试矩阵

 A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]])

高斯·乔丹

 A_1 = npi . gaussjordan ( A . copy ())
I = A @ A_1
I = np . around ( I , 1 )
print ( 'A_1 = n n ' , A_1 )
print ( ' n A_1*A = n n ' , I )

 A_1 =

 [[-24.  18.   5.]
 [ 20. -15.  -4.]
 [ -5.   4.   1.]]

A_1*A =

 [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

基质分解

进口

 import pyoptim . my_numpy . decompose as npd

测试矩阵

 A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]])      #A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ],[ - 1. , 2. , - 1. ],[ 0. , - 1. , 2. ]])  #B is positive definite
Y = np . array ([ 45 , - 78 , 95 ])                               #randomly chosen column vector

鲁

 L , U , P = npd . LU ( A )
print ( "P = n " , P , " n n L = n " , L , " n n U = n " , U )
print ( " n " , A == P @ L @ U )

 P =
 [[0. 0. 1.]
 [0. 1. 0.]
 [1. 0. 0.]] 

L =
 [[1.  0.  0. ]
 [0.  1.  0. ]
 [0.2 0.8 1. ]] 

U =
 [[ 5.   6.   0. ]
 [ 0.   1.   4. ]
 [ 0.   0.  -0.2]]

 [[ True  True  True]
 [ True  True  True]
 [ True  True  True]]

Choleski

 L = npd . choleski ( A )          # A is not positive definite
print ( L )
print ( "--------------------------------------------------" )
L = npd . choleski ( B )          # B is positive definite 
print ( 'L = n ' , L , ' n ' )

C = np . around ( L @( L . T ), 1 )
print ( 'B = L@(L.T) n n ' , B == C )

 A must be positive definite !
None
--------------------------------------------------
L =
 [[ 1.41421356  0.          0.        ]
 [-0.70710678  1.22474487  0.        ]
 [ 0.         -0.81649658  1.15470054]] 

B = L@(L.T) 

 [[ True  True  True]
 [ True  True  True]
 [ True  True  True]]

解决线性系统

进口

 import pyoptim . my_numpy . solve as nps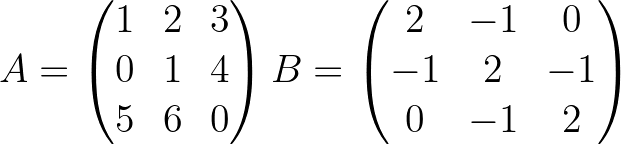

测试矩阵

 A = np . array ([[ 1. , 2. , 3. ], [ 0. , 1. , 4. ], [ 5. , 6. , 0. ]]) # A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ], [ - 1. , 2. , - 1. ], [ 0. , - 1. , 2. ]]) # B is positive definite
Y = np . array ([ 45 , - 78 , 95 ]) # randomly chosen column vector

高斯·乔丹

 X = nps . gaussjordan ( A , Y )
print ( "X = n " , X )
print ( " n A@X=Y n " , A @ X == Y , ' n ' )

print ( '---------------------------------------------------------------' )
X = nps . gaussjordan ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n B@X=Y n " , Y_ == Y , ' n ' )

 X =
 [[-2009.]
 [ 1690.]
 [ -442.]]

 A@X=Y 
 [[ True]
 [ True]
 [ True]] 

---------------------------------------------------------------
X =
 [[18.5]
 [-8. ]
 [43.5]]

 B@X=Y 
 [[ True]
 [ True]
 [ True]]

鲁

 X = nps . LU ( A , Y )
print ( "X* = n " , X )
print ( " n AX*=Y n " , A @ X == Y )
print ( "-------------------------------------------------------------------------------" );
X = nps . LU ( B , Y )
print ( "X* = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y )

 X* =
 [[-2009.]
 [ 1690.]
 [ -442.]]

AX*=Y 
 [[ True]
 [ True]
 [ True]]
-------------------------------------------------------------------------------
X* =
 [[18.5]
 [-8. ]
 [43.5]]

BX*=Y
 [[ True]
 [ True]
 [ True]]

Choleski

 X = nps . choleski ( A , Y )
print ( "-------------------------------------------------------------------------------" )
X = nps . choleski ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y )

 !! A must be positive definite !!
-------------------------------------------------------------------------------
X =
 [[18.5]
 [-8. ]
 [43.5]]

BX*=Y
 [[ True]
 [ True]
 [ True]]

展开