pyoptim 다운로드 pyoptim 소스 코드 다운로드

Pyoptim : 최적화 및 매트릭스 작업을위한 Python 패키지

비교 분석을위한 2D/3D 시각화를 포함하여 약 10 개의 구속되지 않은 최적화 알고리즘을 통합하고 매트릭스 작업을 통합하는 Python 패키지.

이 프로젝트는 ENSIAS의 수치 분석 및 최적화 과정의 구성 요소 인 Mohammed v University 교수 M. Naoum의 제안에서 실험실 세션 중에 실행되는 Python 패키지 캡슐화 알고리즘을 만들기위한 제안에서 발생했습니다. 약 10 개의 구속되지 않은 최적화 알고리즘에 중점을 두어 2D 및 3D 시각화를 제공하여 계산 효율성과 정확도의 성능 비교를 가능하게합니다. 또한이 프로젝트에는 실험실에서 유래 된 알고리즘이 포함 된 패키지 내에 통합 된 역전, 분해 및 선형 시스템 해결과 같은 행렬 작업이 포함됩니다.

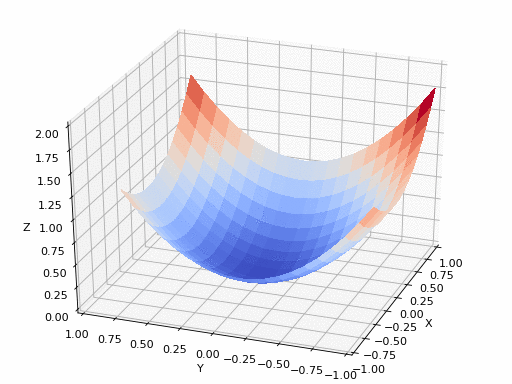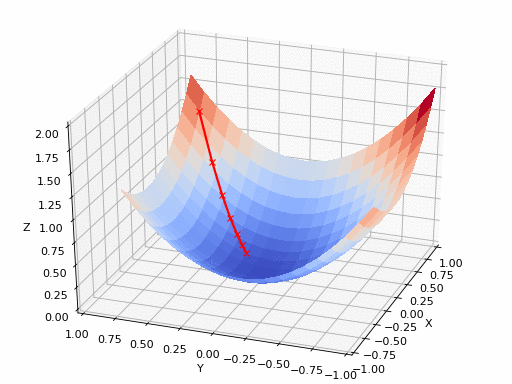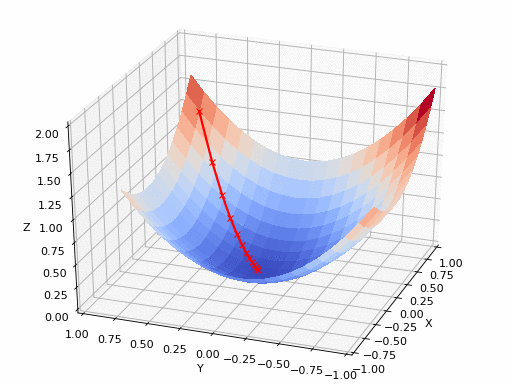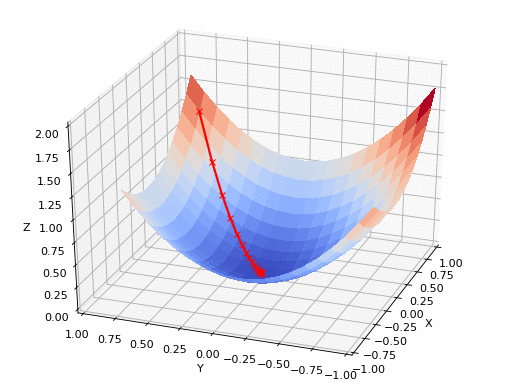
gif 출처 : https://www.nsf.gov/news/mmg/mmg_disp.jsp?med_id_id_id=78950&from= ](https://aria42.com/blog/2014/12/understanding-lbfgs

이 프로젝트의 모든 부분은 다음을 수행하는 방법을 보여주는 샘플 코드입니다.

고정 된 최적화 알고리즘의 구현, 고정 _step, accelerated_step, paridrive_search, dichotomous_search, interval_halving, fibonacci, golden_section, armijo_backward 및 armijo_forward를 포함합니다.
그라디언트 하강, 그라디언트 컨쥬 게이트, 뉴턴, Quasi_Newton_DFP, 확률 적 구배 하강을 포함한 다양한 1 가지 변수 최적화 알고리즘의 통합.
2D, 윤곽 및 3D 형식의 모든 알고리즘에 대한 각 반복 단계의 시각화.
런타임 및 정확도 지표에 중점을 둔 비교 분석을 수행합니다.
반전 (예 : Gauss-Jordan), 분해 (예 : Lu, Choleski) 및 선형 시스템 용 솔루션 (예 : Gauss-Jordan, Lu, Choleski)과 같은 매트릭스 작업의 구현.
시작하기

이 파이썬 패키지를 설치하려면 :

 pip install pyoptim

이 데모 노트북을 실행하십시오

문서 및 비교 분석

단일 변수 최적화 알고리즘
- 라이브러리 가져 오기
- 객관적인 함수
- 매개 변수 초기화
- 고정 단계
- 가속 단계
- 철저한 검색
- 이분법적인 검색
- 간격 절반
- 피보나치
- 골든 _section
- armijo_backward
- armijo_forward
- 비교 분석
다변량 최적화 알고리즘
- 라이브러리 가져 오기
- 객관적인 함수
- 매개 변수 초기화
- 그라디언트 하강
- 그라디언트 컨쥬 게이트
- 뉴턴
- 준 뉴턴 DFP
- 확률 적 구배 하강
- BLS와의 확률 적 구배 하강
- 비교 분석
매트릭스 역수
- 라이브러리 가져 오기
- 테스트 매트릭스
- 가우스 요르단
- 매트릭스 역수
- 매트릭스 역수
매트릭스 분해
- 라이브러리 가져 오기
- 테스트 매트릭스
- 루
- Choleski
선형 시스템 해결
- 라이브러리 가져 오기
- 테스트 매트릭스
- 가우스 요르단
- 루
- Choleski

단일 변수 최적화 알고리즘

라이브러리 가져 오기

 import pyoptim . my_scipy . onevar_optimize . minimize as soom
import pyoptim . my_plot . onevar . _2D as po2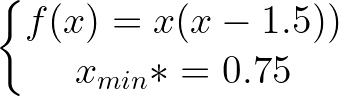

객관적인 함수

 def f ( x ):
    return x * ( x - 1.5 )   # analytically, argmin(f) = 0.75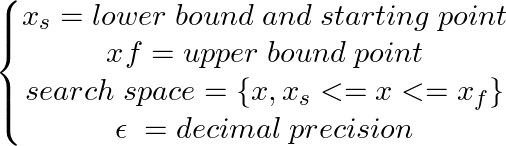

매개 변수 초기화

 xs = - 10
xf = 10
epsilon = 1.e-2

고정 단계

 print ( 'x* =' , soom . fixed_step ( f , xs , epsilon ))
po2 . fixed_step ( f , xs , epsilon )

 x* = 0.75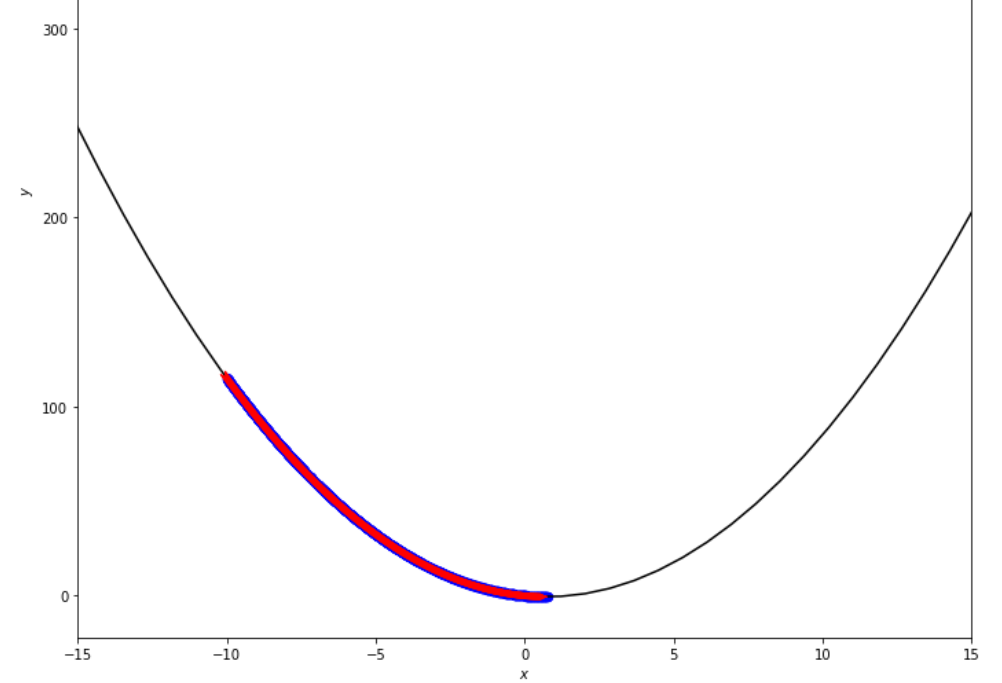

최소에 도달하기 전에 고정 된 단계 알고리즘에 의해 수행 된 단계 순서

가속 단계

 print ( 'x* =' , soom . accelerated_step ( f , xs , epsilon ))
po2 . accelerated_step ( f , xs , epsilon )

 x* = 0.86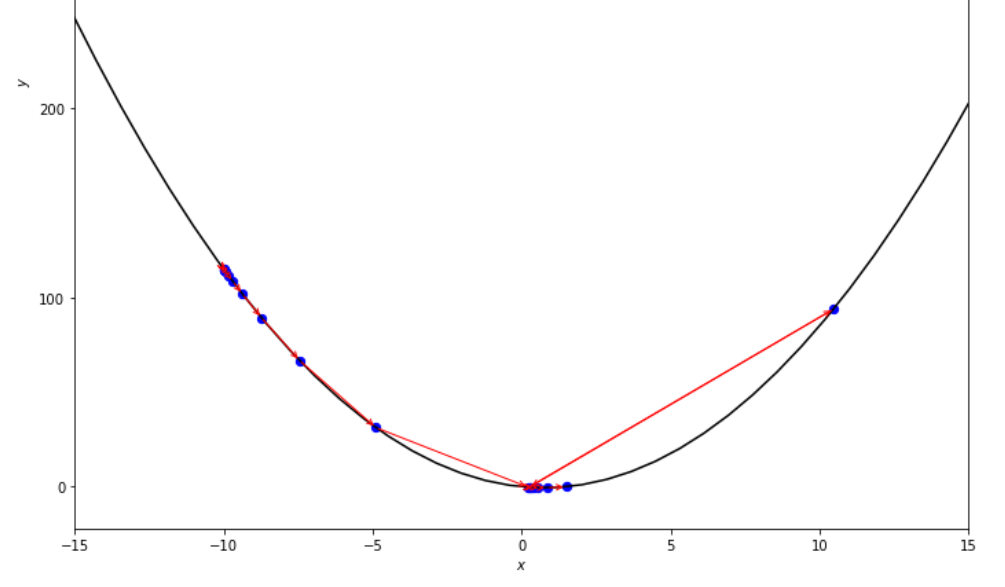

최소에 도달하기 전에 가속 된 단계 알고리즘에 의해 취한 단계의 순서

철저한 검색

 print ( 'x* =' , soom . exhaustive_search ( f , xs , xf , epsilon ))
po2 . exhaustive_search ( f , xs , xf , epsilon )

 x* = 0.75

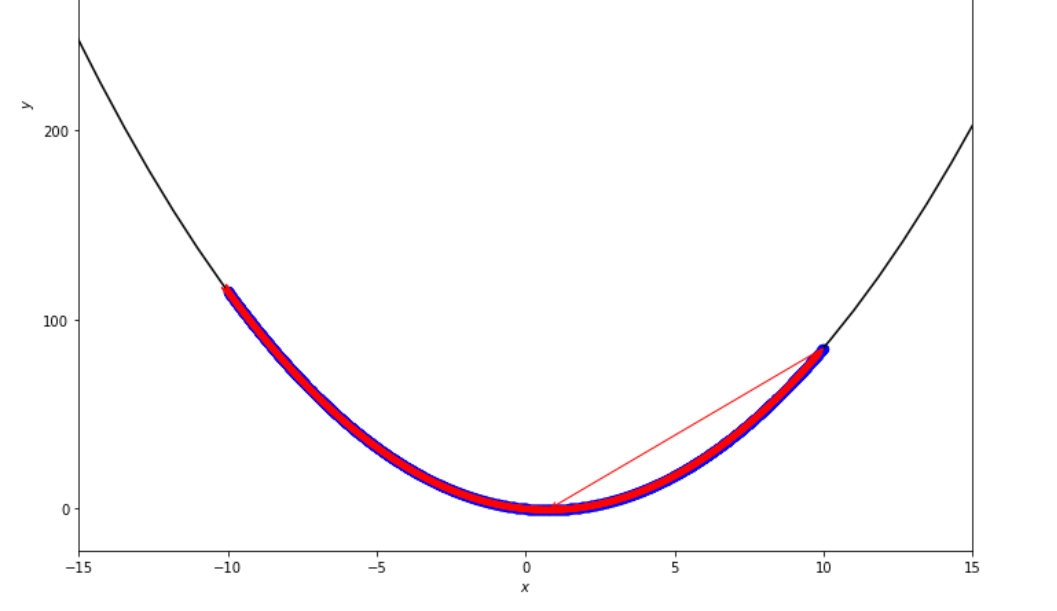
최소에 도달하기 전에 철저한 검색 알고리즘에 의해 수행 된 일련의 단계

이분법적인 검색

 mini_delta = 1.e-3
print ( 'x* =' , soom . dichotomous_search ( f , xs , xf , epsilon , mini_delta ))
po2 . dichotomous_search ( f , xs , xf , epsilon , mini_delta )

 x* = 0.7494742431640624

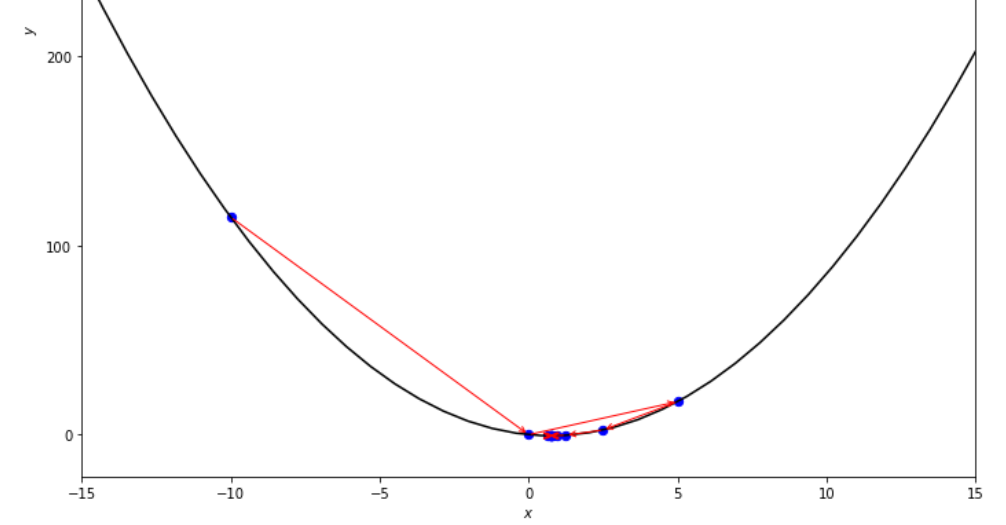
최소에 도달하기 전에 이분법 검색 알고리즘에 의해 수행 된 단계의 순서

간격 절반

 print ( 'x* =' , soom . interval_halving ( f , xs , xf , epsilon ))
po2 . interval_halving ( f , xs , xf , epsilon )

 x* = 0.75

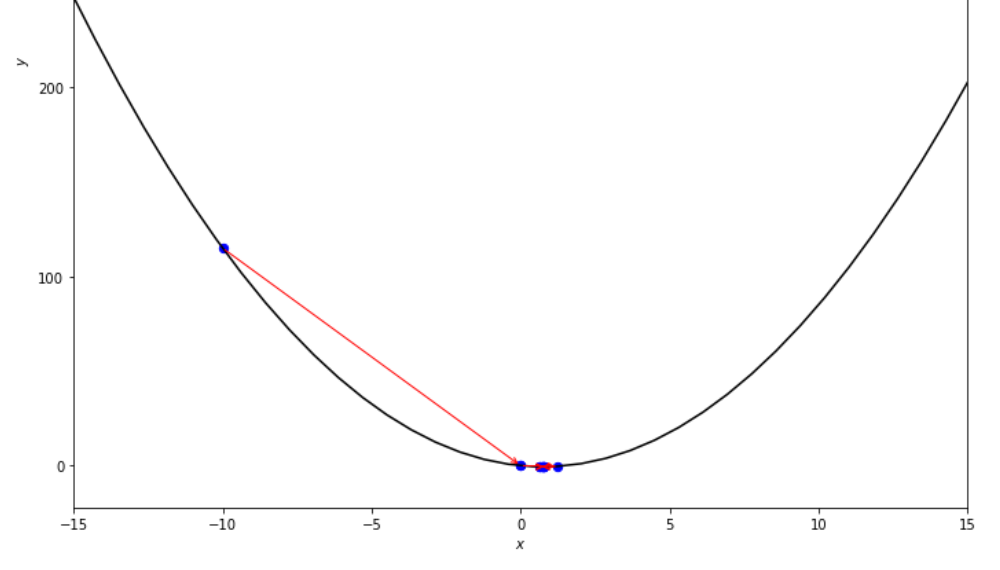
최소에 도달하기 전에 간격 절반 알고리즘에 의해 취한 단계 일련의 단계.

피보나치

 n = 15
print ( 'x* =' , soom . fibonacci ( f , xs , xf , n )) 
po2 . fibonacci ( f , xs , xf , n )

 x* = 0.76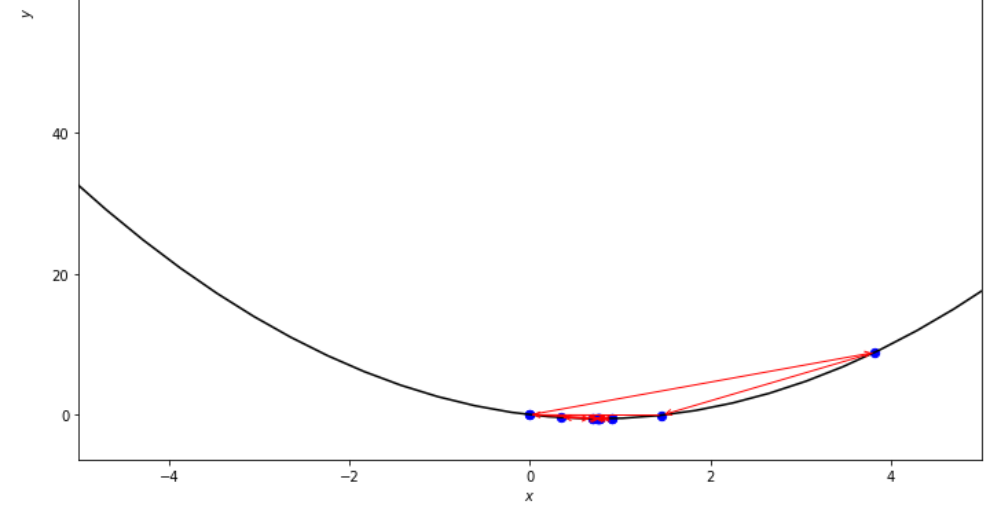

최소에 도달하기 전에 Fibonacci 알고리즘에 의해 취한 단계 일련의 단계.

골든 섹션

 print ( 'x* =' , soom . golden_section ( f , xs , xf , epsilon ))
po2 . golden_section ( f , xs , xf , epsilon )

 x* = 0.75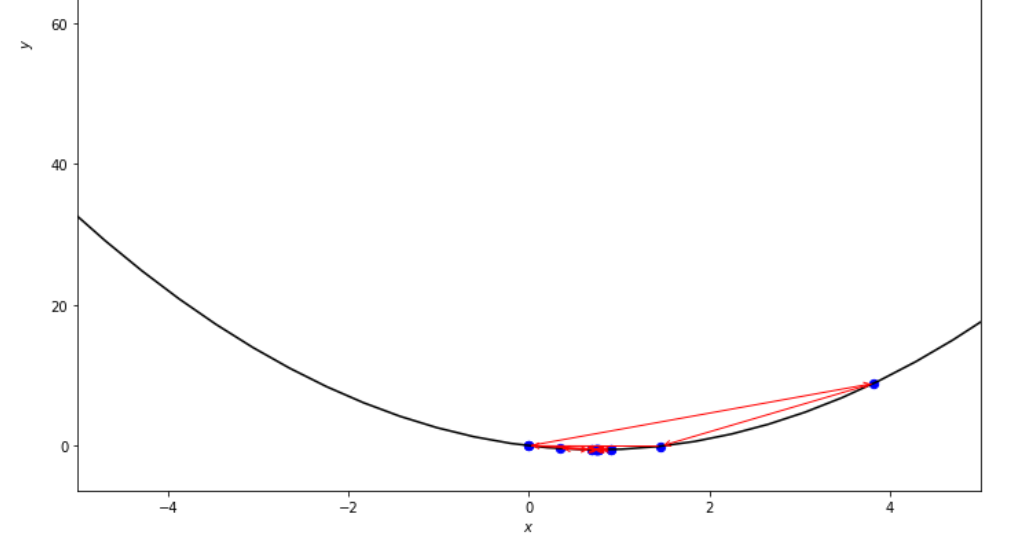

최소값에 도달하기 전에 황금 섹션 알고리즘에 의해 취한 일련의 단계

Armijo 뒤로

 ŋ = 2
xs = 100
print ( 'x* =' , soom . armijo_backward ( f , xs , ŋ , epsilon ))
po2 . armijo_backward ( f , xs , ŋ , epsilon )

 x* = 0.78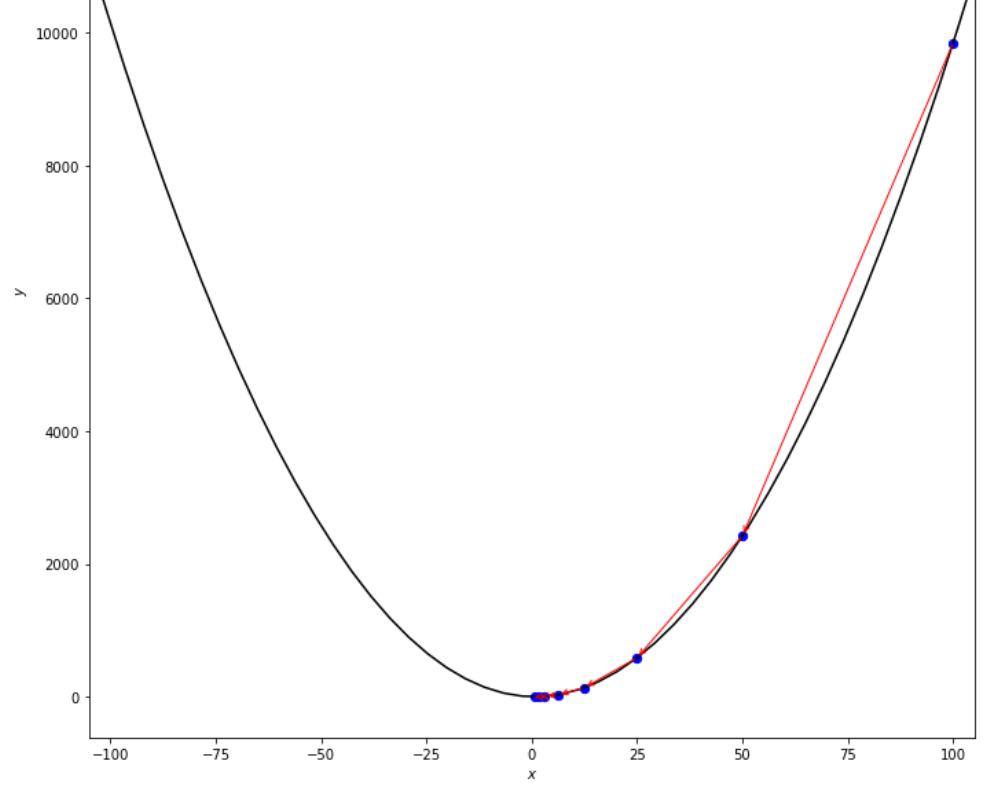

최소에 도달하기 전에 Armijo Backward 알고리즘이 수행 한 단계의 순서

Armijo Forward

 xs = 0.1
epsilon = 0.5
ŋ = 2
print ( 'x* =' , soom . armijo_forward ( f , xs , ŋ , epsilon ))
po2 . armijo_forward ( f , xs , ŋ , epsilon )

 x* = 0.8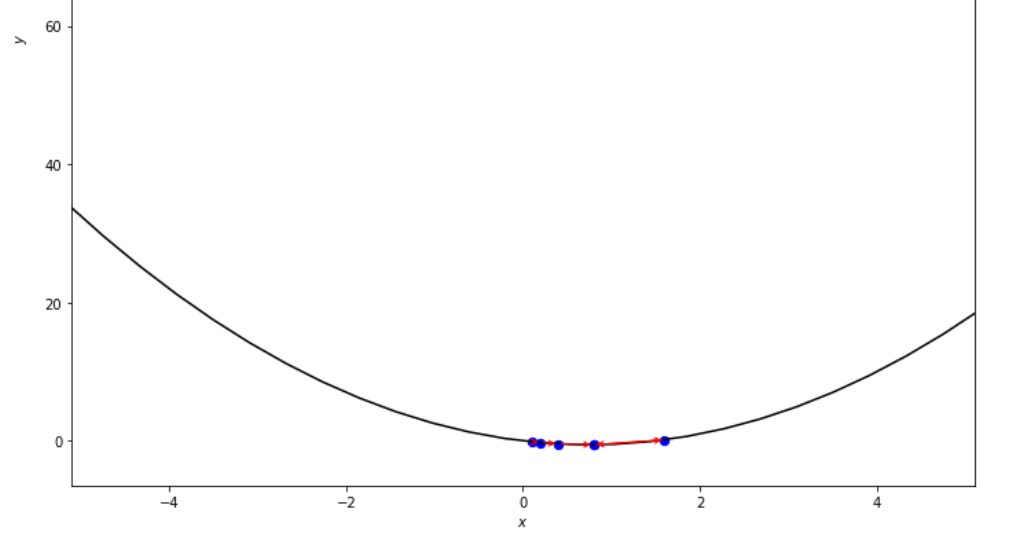

최소에 도달하기 전에 Armijo Forward 알고리즘이 수행 한 단계의 순서

비교 분석

 po2 . compare_all_time ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 )

실행 시간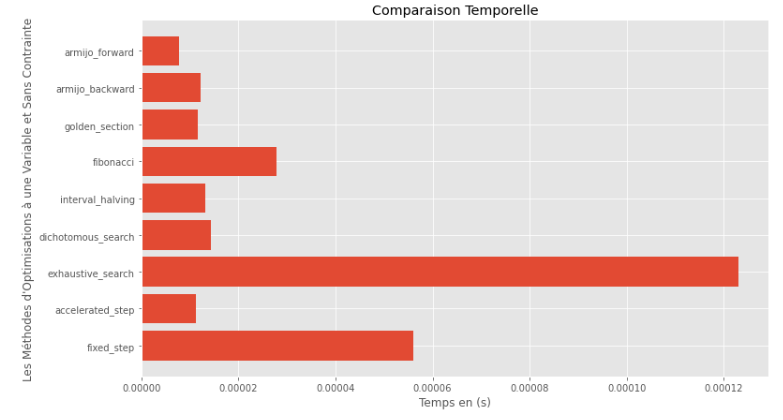

 po2 . compare_all_precision ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 )

True와 Computed Minims 사이의 간격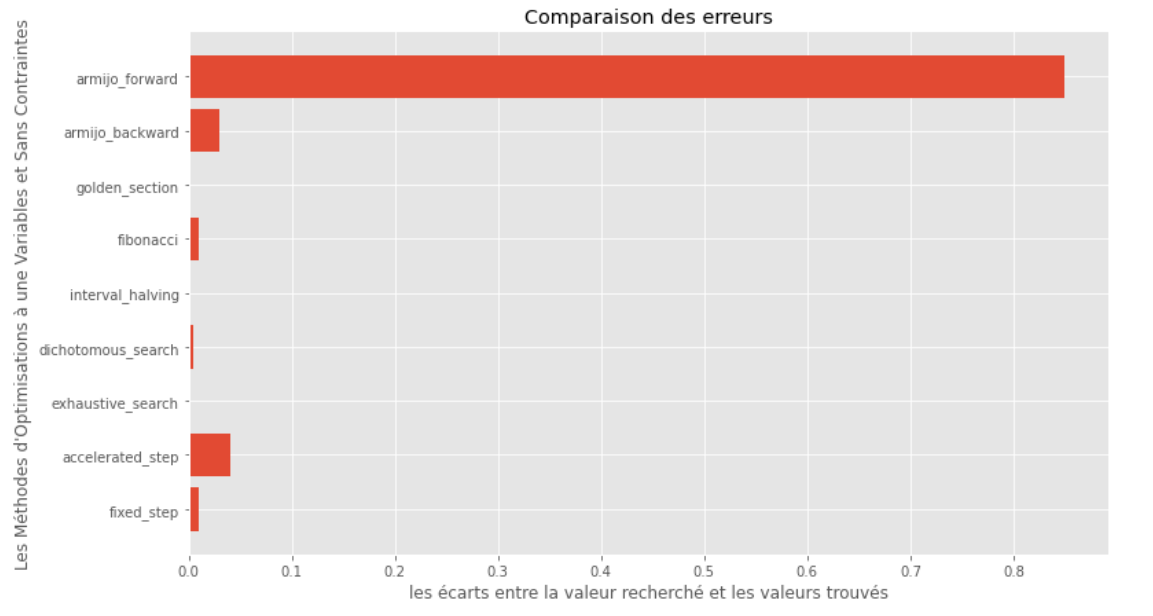

런타임 및 정확도 그래프 에서이 볼록 단일 변수 기능에 대해 평가 된 알고리즘 중에서 골든 섹션 방법이 최적의 선택으로 나타나서 높은 정확도와 특히 낮은 런타임을 제공한다는 것을 추론 할 수 있습니다.

다변량 최적화 알고리즘

라이브러리 가져 오기

 import pyoptim . my_plot . multivar . _3D as pm3
import pyoptim . my_plot . multivar . contour2D as pmc

객관적인 함수

 def h ( x ):
    return x [ 0 ] - x [ 1 ] + 2 * ( x [ 0 ] ** 2 ) + 2 * x [ 1 ] * x [ 0 ] + x [ 1 ] ** 2
# analytically, argmin(f) = [-1, 1.5]

항문 솔루션

매개 변수 초기화

 X = [ 1000 , 897 ]
alpha = 1.e-2
tol = 1.e-2

그라디언트 하강

 pmc . gradient_descent ( h , X , tol , alpha )
pm3 . gradient_descent ( h , X , tol , alpha )

 Y* =  [-1.01  1.51]

최소에 도달하기 전에 그라디언트 하강 알고리즘에 의해 수행 된 단계의 순서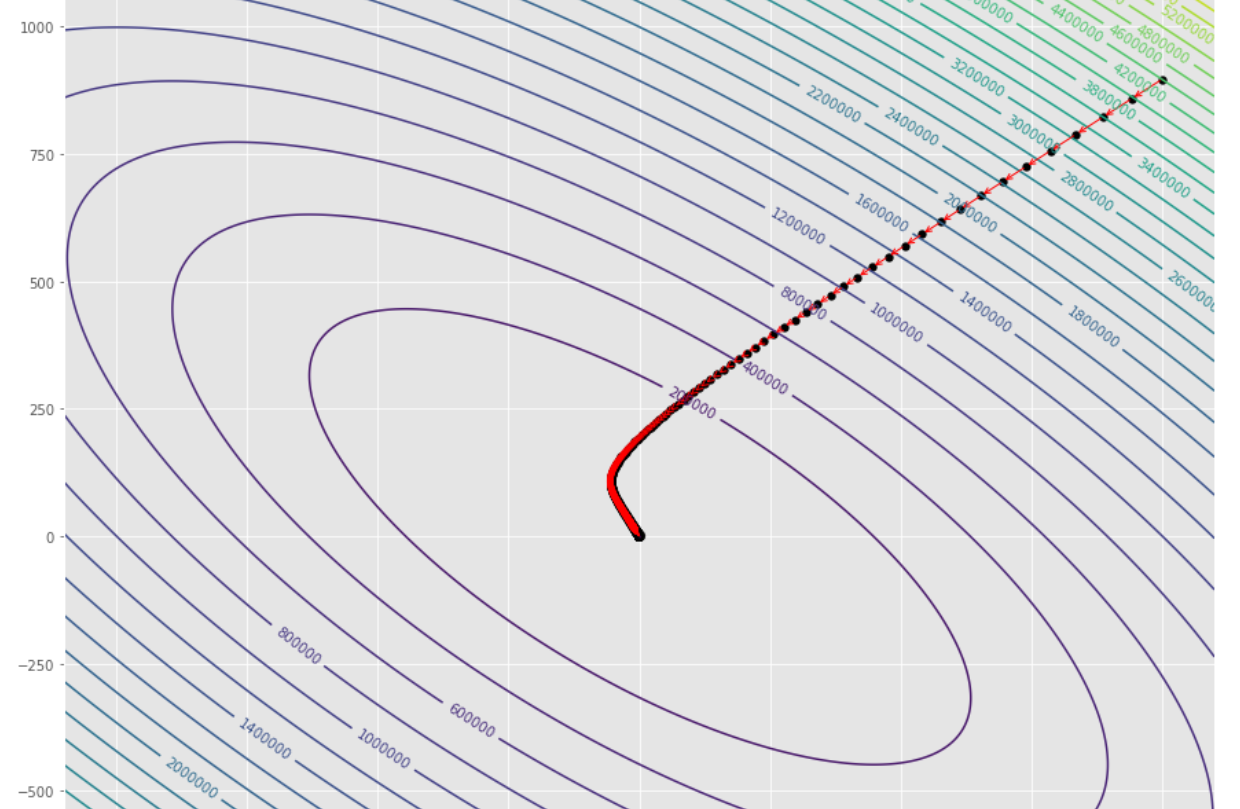

윤곽 줄거리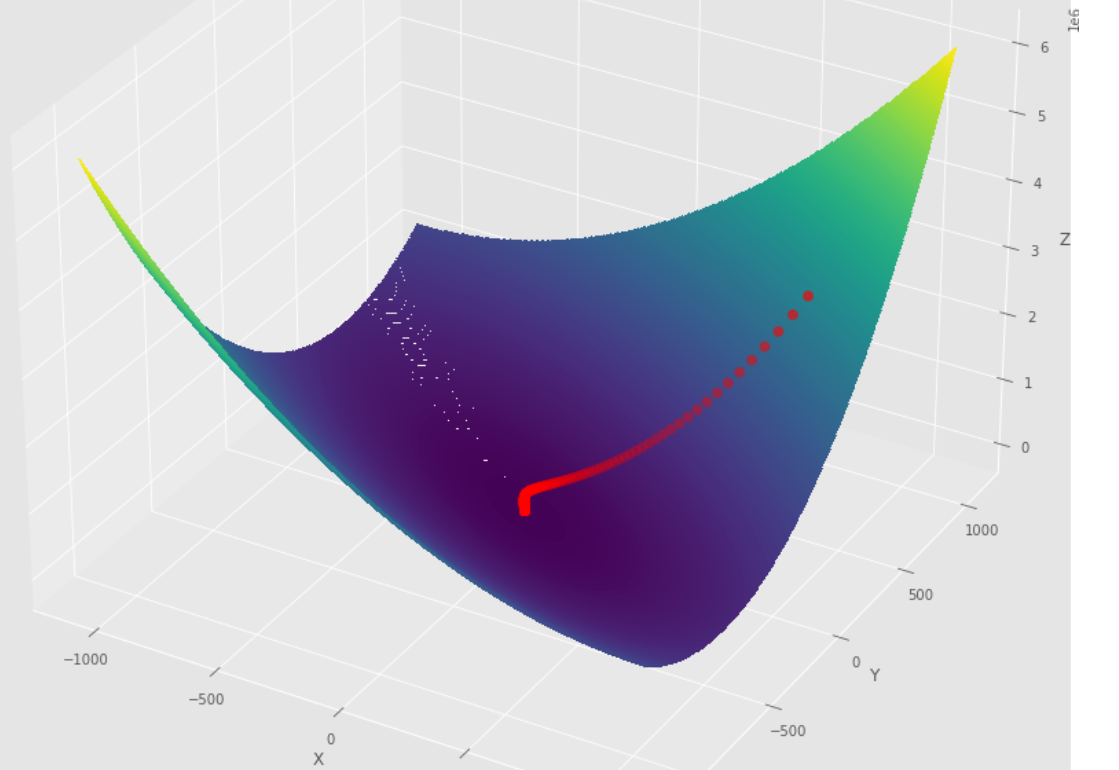

3D 플롯

그라디언트 컨쥬 게이트

 pmc . gradient_conjugate ( h , X , tol )
pm3 . gradient_conjugate ( h , X , tol )

 Y* =  [-107.38  172.18]

최소에 도달하기 전에 그라디언트 컨쥬 게이트 알고리즘에 의해 수행 된 단계의 순서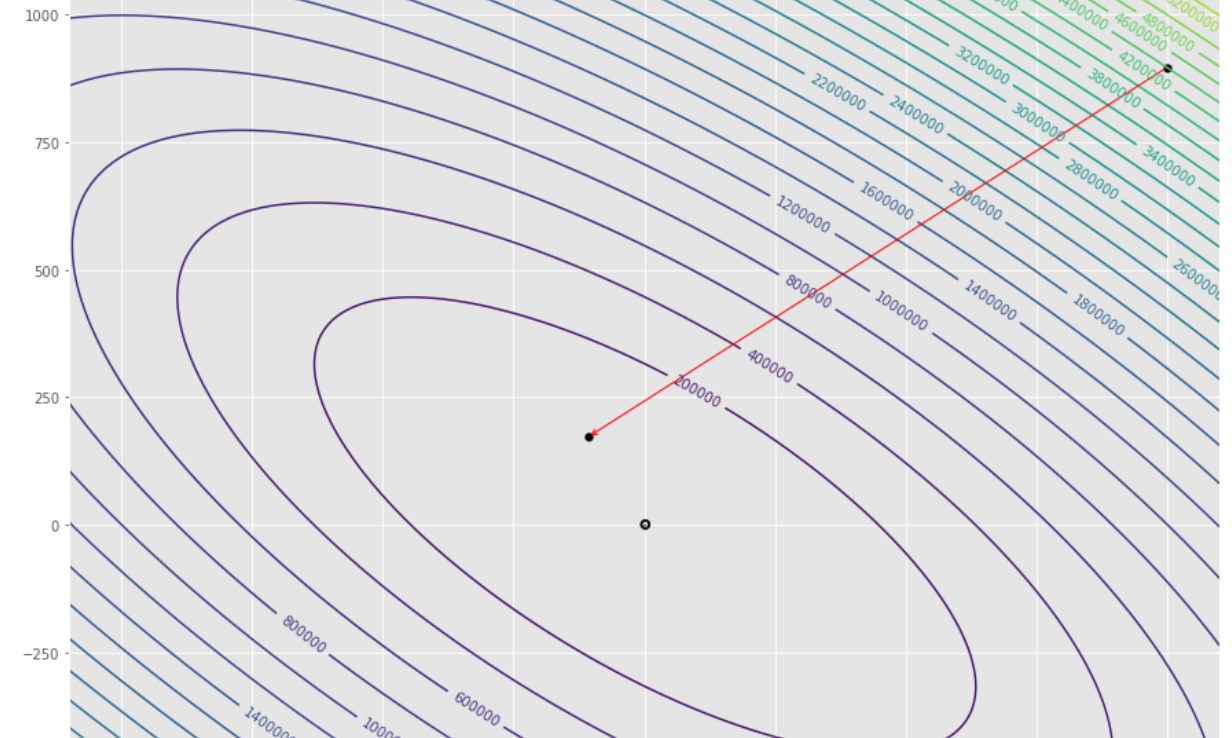

윤곽 줄거리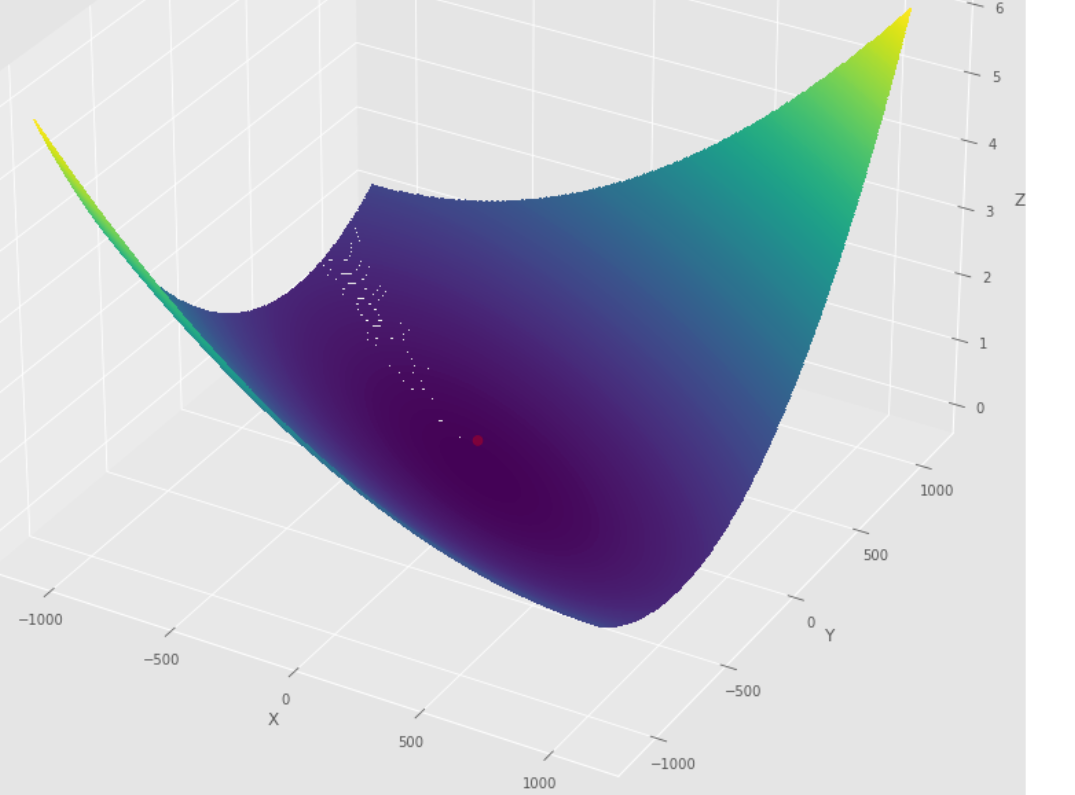

3D 플롯

뉴턴

 pmc . newton ( h , X , tol )
pm3 . newton ( h , X , tol )

 Y* =  [-1.   1.5]

최소에 도달하기 전에 Newton 알고리즘에 의해 수행 된 일련의 단계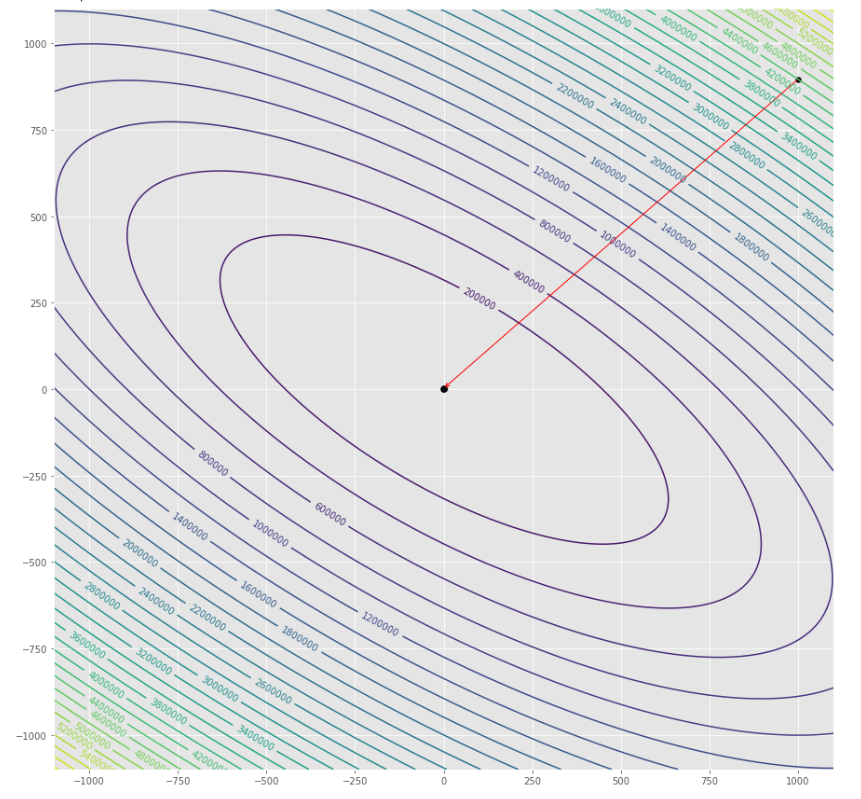

윤곽 줄거리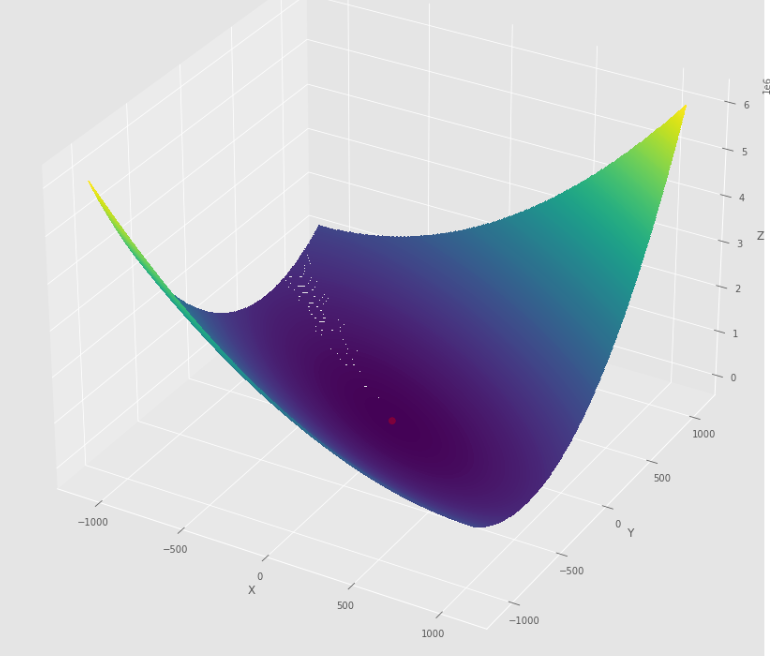

3D 플롯

준 뉴턴 DFP

 pmc . quasi_newton_dfp ( h , X , tol )
pm3 . quasi_newton_dfp ( h , X , tol )

 Y* =  [-1.   1.5]

최소에 도달하기 전에 Quasi Newton DFP 알고리즘에 의해 수행 된 단계의 순서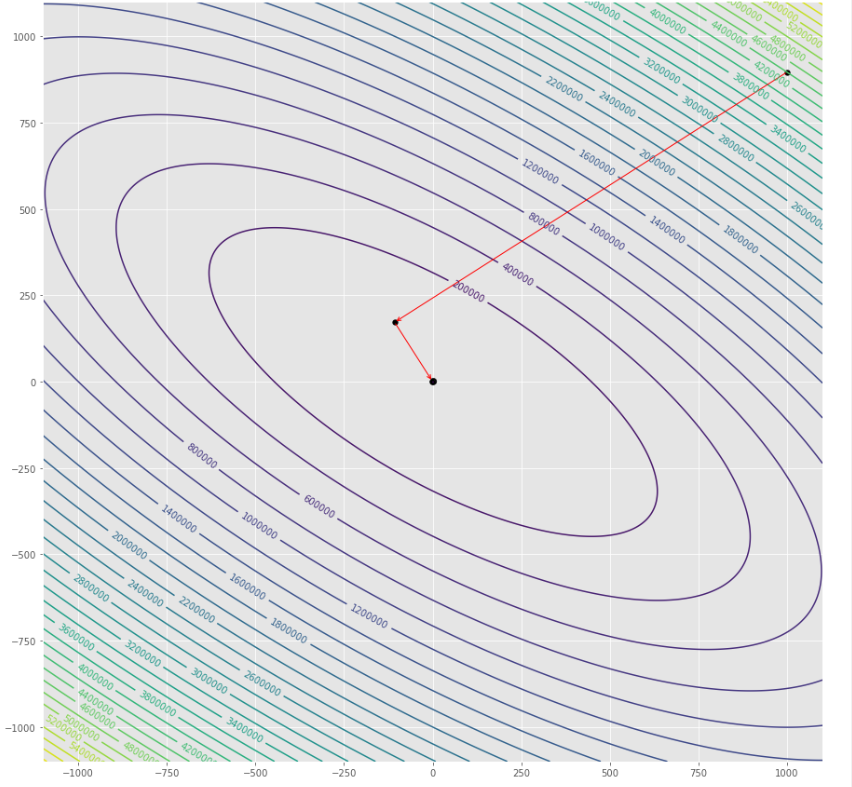

윤곽 줄거리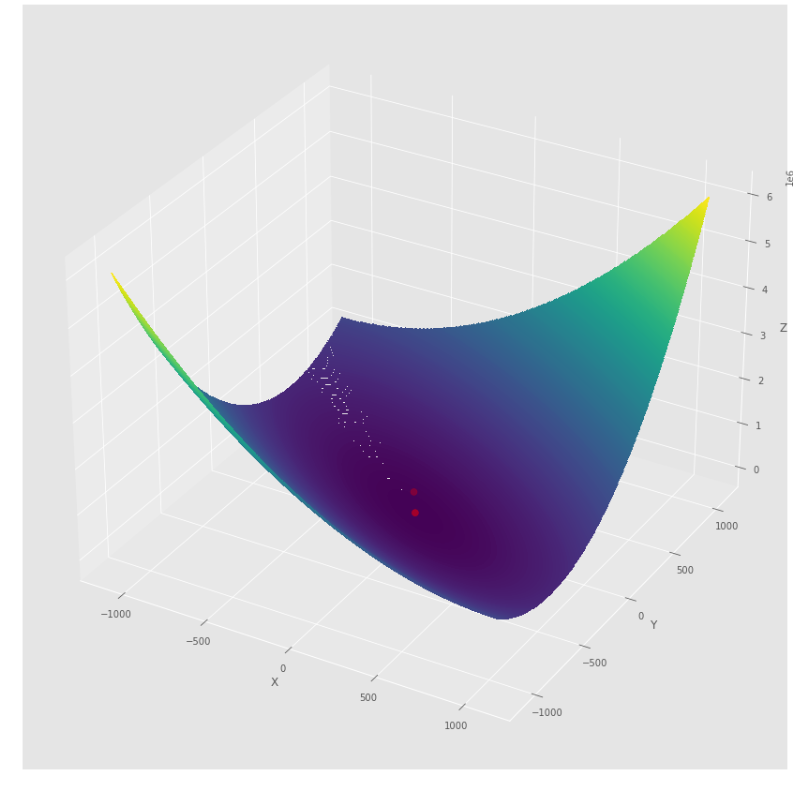

3D 플롯

확률 적 구배 하강

 pmc . sgd ( h , X , tol , alpha )
pm3 . sgd ( h , X , tol , alpha )

 Y* =  [-1.01  1.52]

최소에 도달하기 전에 확률 적 구배 하강 알고리즘에 의해 수행 된 단계의 순서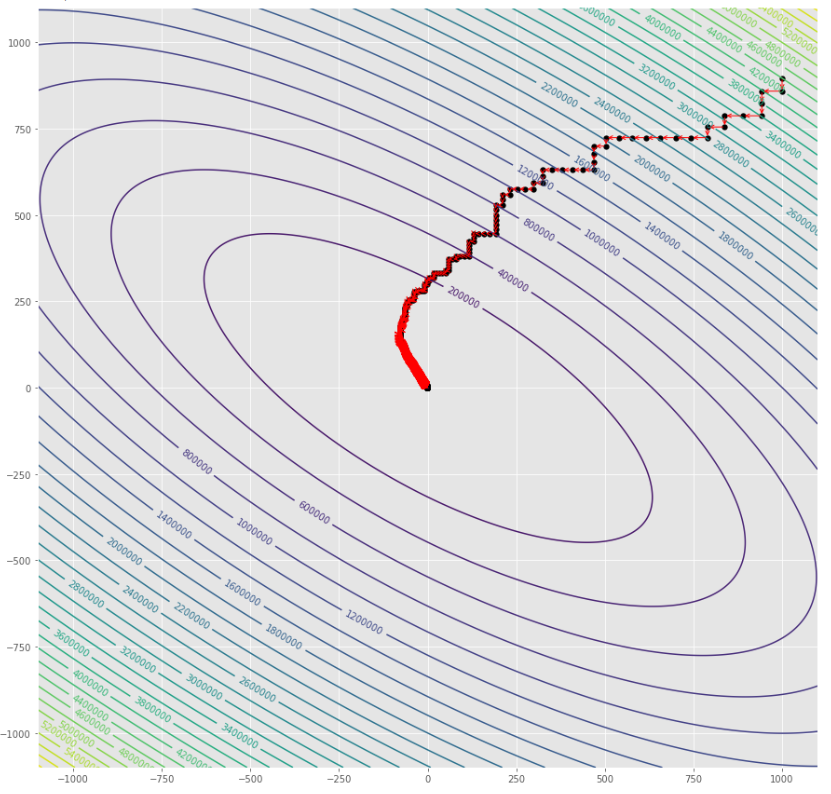

윤곽 줄거리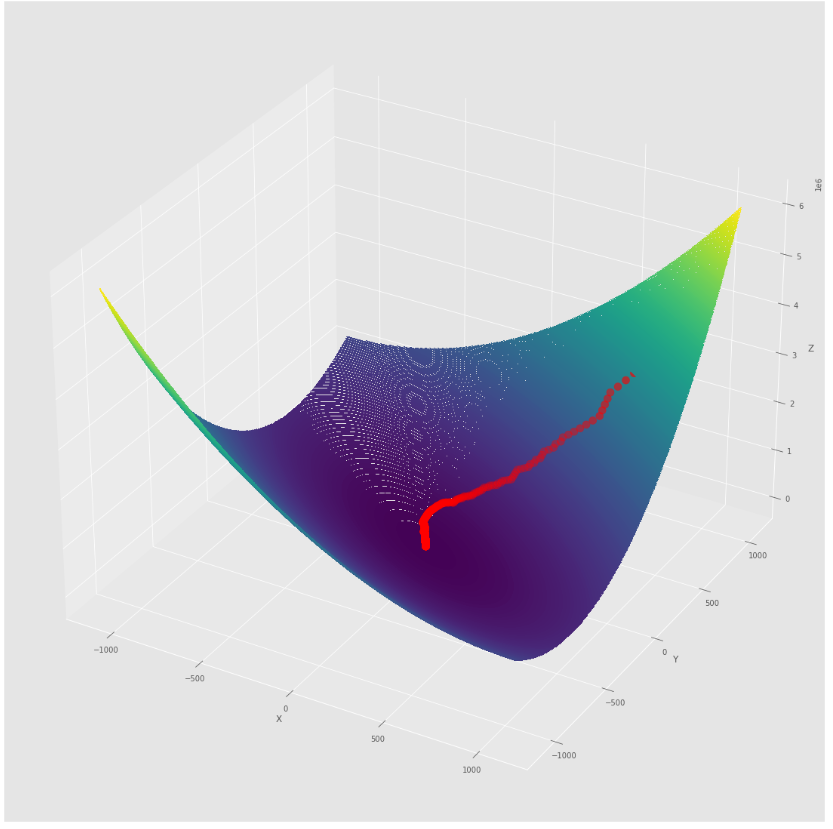

3D 플롯

BLS와의 확률 적 구배 하강

 alpha = 100 #it must be high because of BLS
c = 2
pmc . sgd_with_bls ( h , X , tol , alpha , c ) 
pm3 . sgd_with_bls ( h , X , tol , alpha , c )

 Y* =  [-1.   1.5]

최소에 도달하기 전에 BLS 알고리즘으로 확률 론적 구배 출신에 의해 취해진 단계의 순서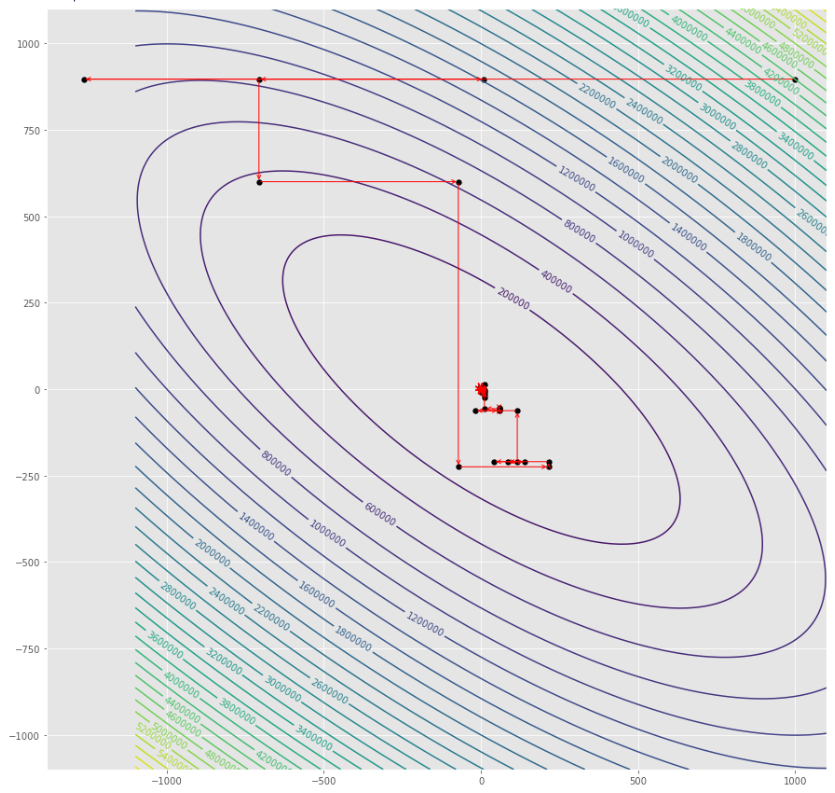

윤곽 줄거리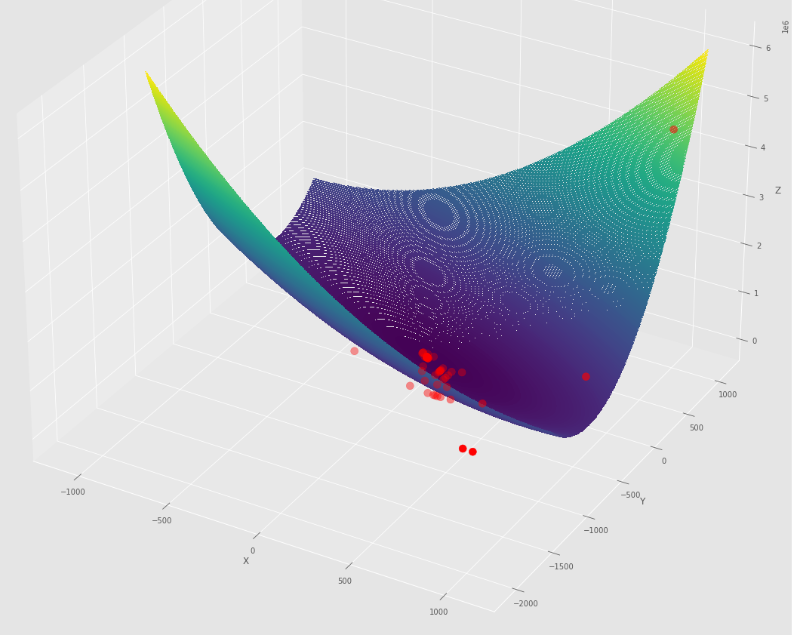

3D 플롯

비교 분석

 pm3 . compare_all_time ( h , X , 1.e-2 , 1.e-1 , 100 , 2 )

실행 시간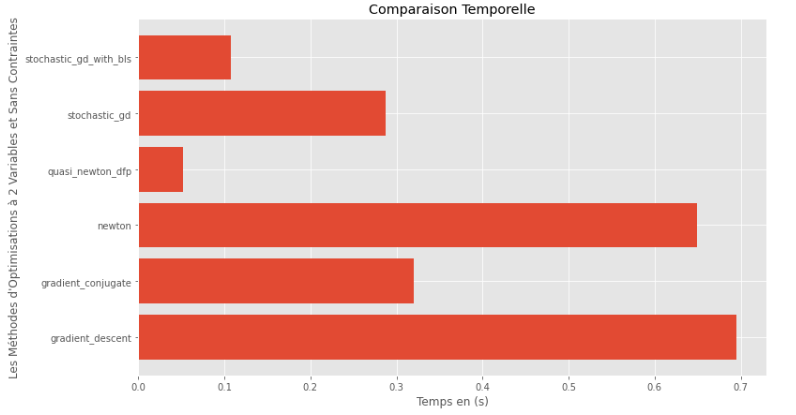

 pm3 . compare_all_precision ( h , X , 1.e-2 , 1.e-1 , 100 , 2 )

True와 Computed Minims 사이의 간격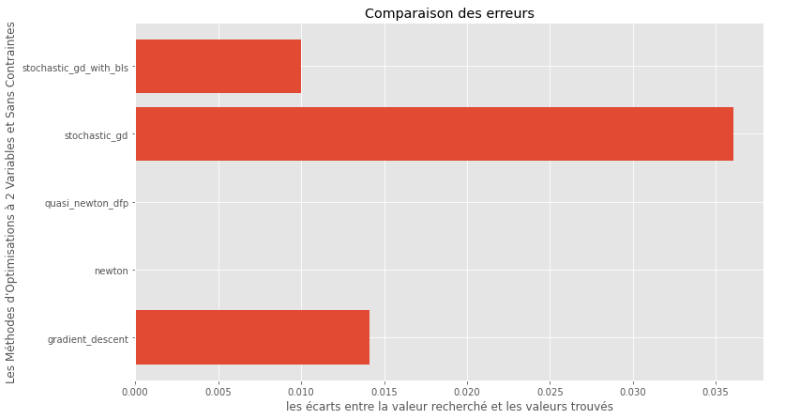

런타임 및 정확도 그래프 에서이 볼록한 다변량 함수에 대해 평가 된 알고리즘 중 Quasi Newton DFP 방법은 최적의 선택으로 나타나서 높은 정확도와 특히 런타임이 혼합되어 있음을 추론 할 수 있습니다.

매트릭스 역수

수입 도서관

 import pyoptim . my_numpy . inverse as npi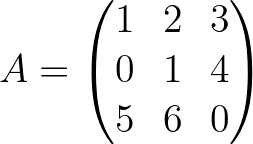

테스트 매트릭스

 A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]])

가우스 요르단

 A_1 = npi . gaussjordan ( A . copy ())
I = A @ A_1
I = np . around ( I , 1 )
print ( 'A_1 = n n ' , A_1 )
print ( ' n A_1*A = n n ' , I )

 A_1 =

 [[-24.  18.   5.]
 [ 20. -15.  -4.]
 [ -5.   4.   1.]]

A_1*A =

 [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

매트릭스 분해

수입

 import pyoptim . my_numpy . decompose as npd

테스트 매트릭스

 A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]])      #A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ],[ - 1. , 2. , - 1. ],[ 0. , - 1. , 2. ]])  #B is positive definite
Y = np . array ([ 45 , - 78 , 95 ])                               #randomly chosen column vector

루

 L , U , P = npd . LU ( A )
print ( "P = n " , P , " n n L = n " , L , " n n U = n " , U )
print ( " n " , A == P @ L @ U )

 P =
 [[0. 0. 1.]
 [0. 1. 0.]
 [1. 0. 0.]] 

L =
 [[1.  0.  0. ]
 [0.  1.  0. ]
 [0.2 0.8 1. ]] 

U =
 [[ 5.   6.   0. ]
 [ 0.   1.   4. ]
 [ 0.   0.  -0.2]]

 [[ True  True  True]
 [ True  True  True]
 [ True  True  True]]

Choleski

 L = npd . choleski ( A )          # A is not positive definite
print ( L )
print ( "--------------------------------------------------" )
L = npd . choleski ( B )          # B is positive definite 
print ( 'L = n ' , L , ' n ' )

C = np . around ( L @( L . T ), 1 )
print ( 'B = L@(L.T) n n ' , B == C )

 A must be positive definite !
None
--------------------------------------------------
L =
 [[ 1.41421356  0.          0.        ]
 [-0.70710678  1.22474487  0.        ]
 [ 0.         -0.81649658  1.15470054]] 

B = L@(L.T) 

 [[ True  True  True]
 [ True  True  True]
 [ True  True  True]]

선형 시스템 해결

수입

 import pyoptim . my_numpy . solve as nps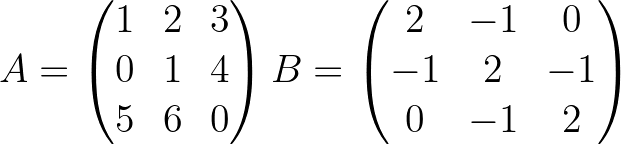

테스트 매트릭스

 A = np . array ([[ 1. , 2. , 3. ], [ 0. , 1. , 4. ], [ 5. , 6. , 0. ]]) # A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ], [ - 1. , 2. , - 1. ], [ 0. , - 1. , 2. ]]) # B is positive definite
Y = np . array ([ 45 , - 78 , 95 ]) # randomly chosen column vector

가우스 요르단

 X = nps . gaussjordan ( A , Y )
print ( "X = n " , X )
print ( " n A@X=Y n " , A @ X == Y , ' n ' )

print ( '---------------------------------------------------------------' )
X = nps . gaussjordan ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n B@X=Y n " , Y_ == Y , ' n ' )

 X =
 [[-2009.]
 [ 1690.]
 [ -442.]]

 A@X=Y 
 [[ True]
 [ True]
 [ True]] 

---------------------------------------------------------------
X =
 [[18.5]
 [-8. ]
 [43.5]]

 B@X=Y 
 [[ True]
 [ True]
 [ True]]

루

 X = nps . LU ( A , Y )
print ( "X* = n " , X )
print ( " n AX*=Y n " , A @ X == Y )
print ( "-------------------------------------------------------------------------------" );
X = nps . LU ( B , Y )
print ( "X* = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y )

 X* =
 [[-2009.]
 [ 1690.]
 [ -442.]]

AX*=Y 
 [[ True]
 [ True]
 [ True]]
-------------------------------------------------------------------------------
X* =
 [[18.5]
 [-8. ]
 [43.5]]

BX*=Y
 [[ True]
 [ True]
 [ True]]

Choleski

 X = nps . choleski ( A , Y )
print ( "-------------------------------------------------------------------------------" )
X = nps . choleski ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y )

 !! A must be positive definite !!
-------------------------------------------------------------------------------
X =
 [[18.5]
 [-8. ]
 [43.5]]

BX*=Y
 [[ True]
 [ True]
 [ True]]

확장하다