Pyoptim: แพ็คเกจ Python สำหรับการเพิ่มประสิทธิภาพและการดำเนินการเมทริกซ์
โครงการนี้เป็นส่วนประกอบของหลักสูตรการวิเคราะห์เชิงตัวเลขและการเพิ่มประสิทธิภาพที่ Ensias มหาวิทยาลัยโมฮัมเหม็ดวีเกิดขึ้นจากคำแนะนำของศาสตราจารย์เอ็มนูมเพื่อสร้างแพ็คเกจ Python ที่ห่อหุ้มอัลกอริทึมที่ฝึกฝนในระหว่างการประชุมห้องปฏิบัติการ มันมุ่งเน้นไปที่อัลกอริทึมการเพิ่มประสิทธิภาพประมาณสิบอัลกอริทึมที่เสนอการสร้างภาพข้อมูล 2D และ 3D ทำให้สามารถเปรียบเทียบประสิทธิภาพในประสิทธิภาพการคำนวณและความแม่นยำ นอกจากนี้โครงการยังรวมถึงการดำเนินการเมทริกซ์เช่นการผกผันการสลายตัวและการแก้ปัญหาระบบเชิงเส้นทั้งหมดรวมอยู่ในแพ็คเกจที่มีอัลกอริทึมที่ได้จากห้องปฏิบัติการ
แหล่งที่มาของ GIF: https://www.nsf.gov/news/mmg/mmg_disp.jsp?med_id=78950&from= เหมือน
ทุกส่วนของโครงการนี้เป็นรหัสตัวอย่างซึ่งแสดงวิธีการทำสิ่งต่อไปนี้:
การใช้อัลกอริทึมการเพิ่มประสิทธิภาพแบบตัวแปรเดียวรวมถึงการรวม appelerated_step, dichotomous_search, interval_halving, fibonacci, golden_section, armijo_backward และ armijo_forward
การรวมตัวกันของอัลกอริธึมการปรับให้เหมาะสมแบบหนึ่งตัวแปรรวมถึงการไล่ระดับสี, การไล่ระดับสีคอนจูเกต, นิวตัน, quasi_Newton_DFP, การไล่ระดับสีแบบสโทแคสติก
การสร้างภาพข้อมูลของแต่ละขั้นตอนการวนซ้ำสำหรับอัลกอริทึมทั้งหมดในรูปแบบ 2D, contour และ 3D
ดำเนินการวิเคราะห์เปรียบเทียบที่มุ่งเน้นไปที่การวัดรันไทม์และความแม่นยำ
การดำเนินการของการดำเนินการเมทริกซ์เช่นการผกผัน (เช่นเกาส์-จอร์แดน), การสลายตัว (เช่นลู, choleski) และโซลูชันสำหรับระบบเชิงเส้น (เช่นเกาส์-จอร์แดน, ลู, choleski)
ในการติดตั้งแพ็คเกจ Python นี้:
pip install pyoptimเรียกใช้สมุดบันทึกตัวอย่างนี้
import pyoptim . my_scipy . onevar_optimize . minimize as soom
import pyoptim . my_plot . onevar . _2D as po2 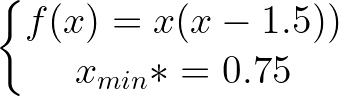
def f ( x ):
return x * ( x - 1.5 ) # analytically, argmin(f) = 0.75 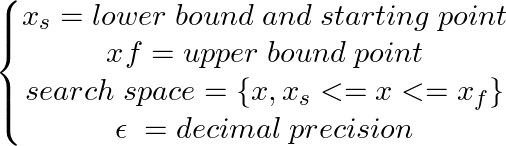
xs = - 10
xf = 10
epsilon = 1.e-2 print ( 'x* =' , soom . fixed_step ( f , xs , epsilon ))
po2 . fixed_step ( f , xs , epsilon ) x* = 0.75 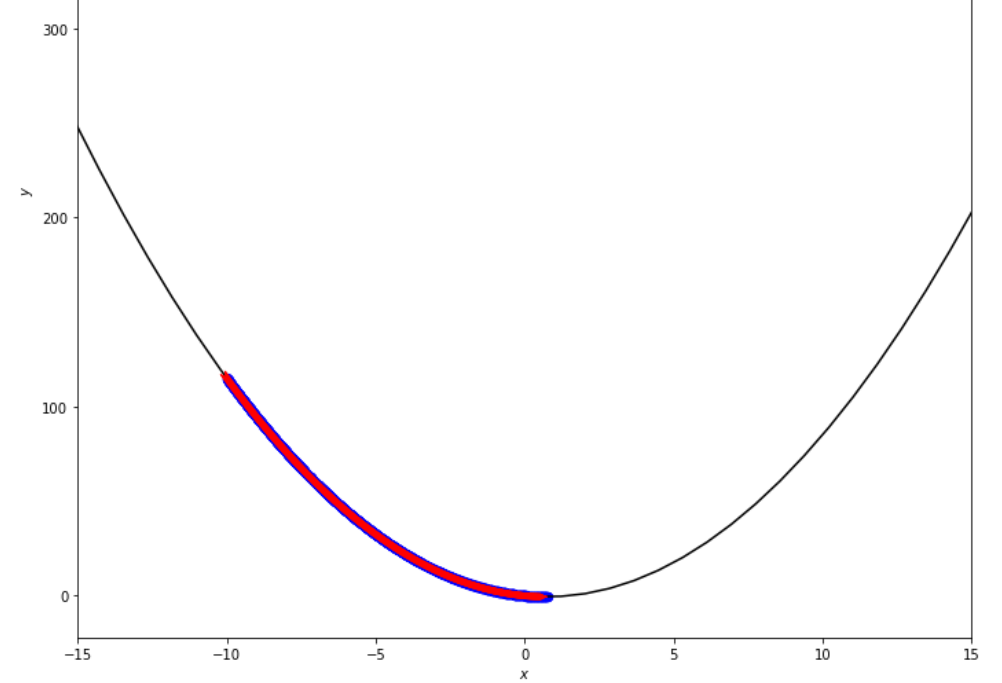
ลำดับของขั้นตอนที่ดำเนินการโดยอัลกอริทึมขั้นตอนคงที่ก่อนถึงขั้นต่ำ
print ( 'x* =' , soom . accelerated_step ( f , xs , epsilon ))
po2 . accelerated_step ( f , xs , epsilon ) x* = 0.86 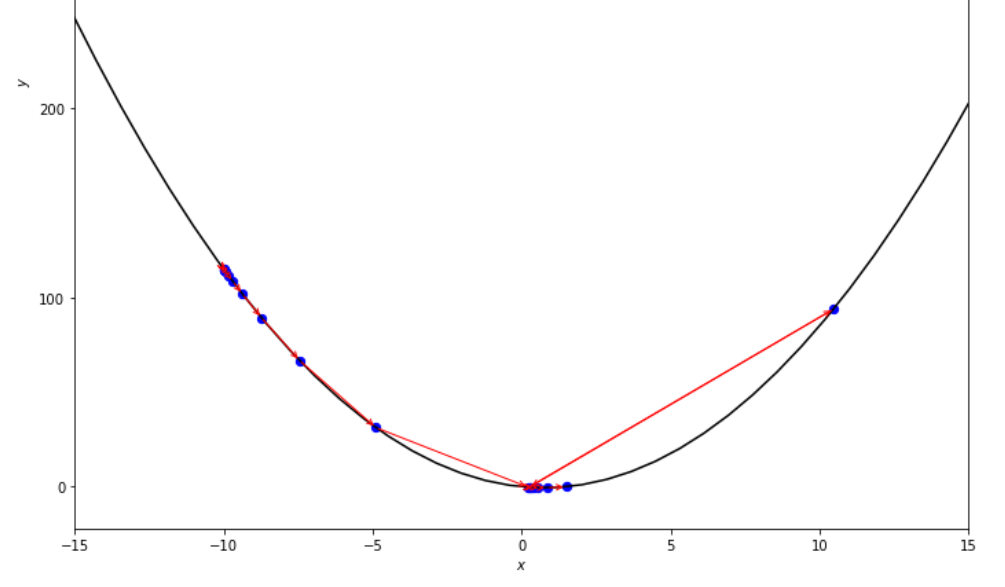
ลำดับของขั้นตอนที่ดำเนินการโดยอัลกอริทึมขั้นตอนเร่งด่วนก่อนถึงขั้นต่ำ
print ( 'x* =' , soom . exhaustive_search ( f , xs , xf , epsilon ))
po2 . exhaustive_search ( f , xs , xf , epsilon ) x* = 0.75
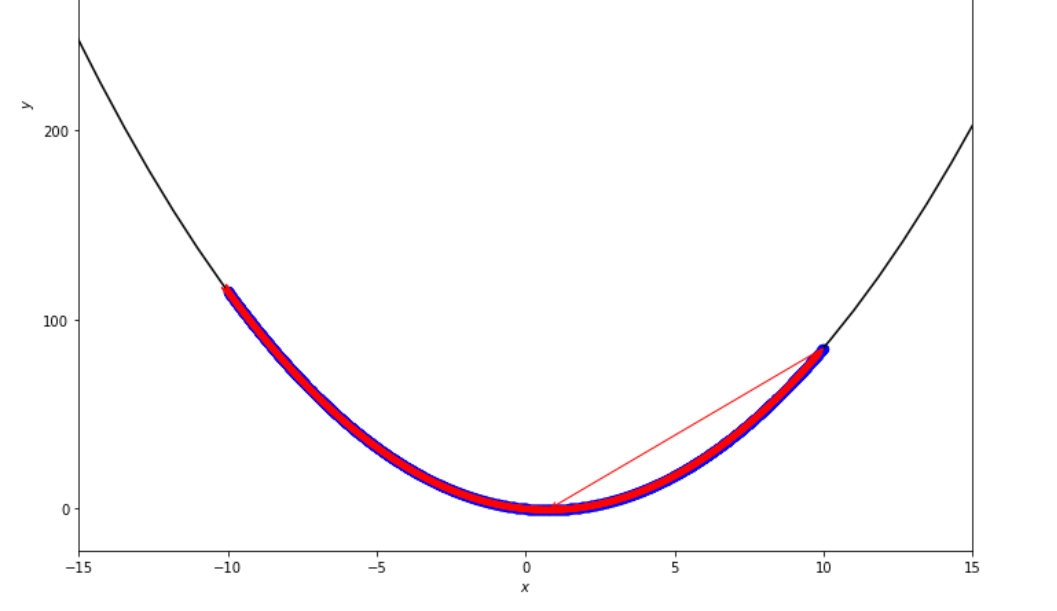
ลำดับของขั้นตอนที่ดำเนินการโดยอัลกอริทึมการค้นหาอย่างละเอียดก่อนถึงขั้นต่ำ
mini_delta = 1.e-3
print ( 'x* =' , soom . dichotomous_search ( f , xs , xf , epsilon , mini_delta ))
po2 . dichotomous_search ( f , xs , xf , epsilon , mini_delta ) x* = 0.7494742431640624
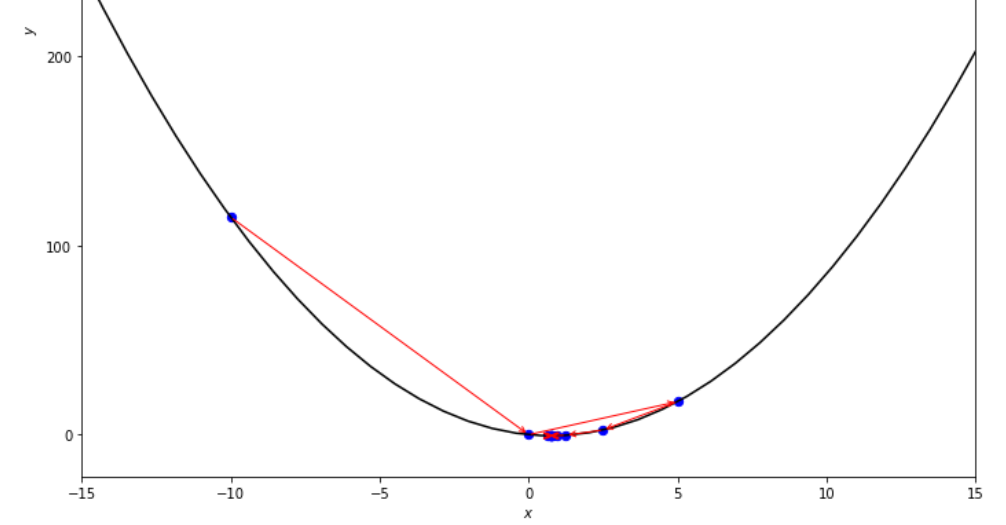
ลำดับของขั้นตอนที่ดำเนินการโดยอัลกอริทึมการค้นหาแบบ dichotomous ก่อนถึงขั้นต่ำ
print ( 'x* =' , soom . interval_halving ( f , xs , xf , epsilon ))
po2 . interval_halving ( f , xs , xf , epsilon ) x* = 0.75
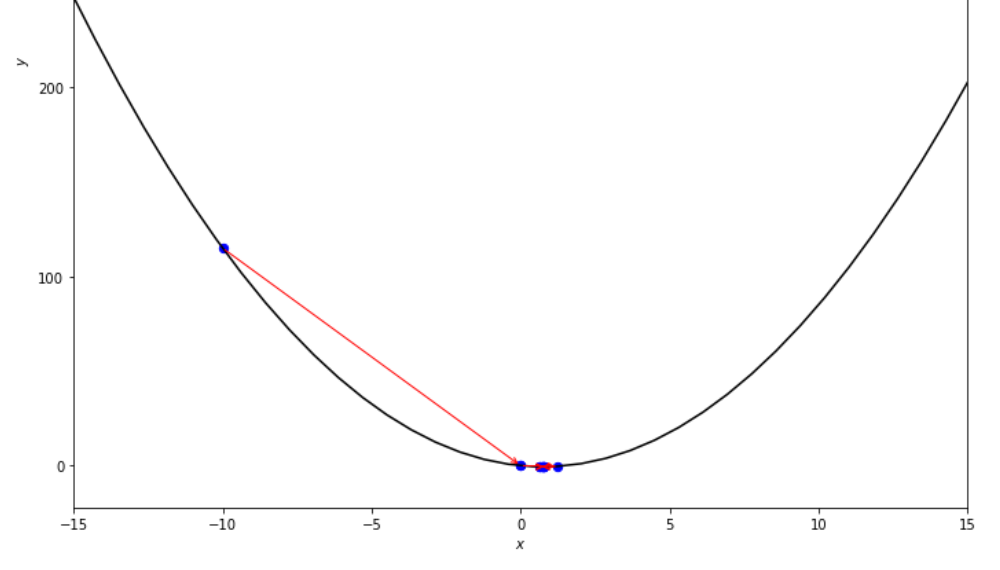
ลำดับของขั้นตอนที่ดำเนินการโดยอัลกอริทึมการลดช่วงเวลาก่อนที่จะถึงขั้นต่ำ
n = 15
print ( 'x* =' , soom . fibonacci ( f , xs , xf , n ))
po2 . fibonacci ( f , xs , xf , n ) x* = 0.76 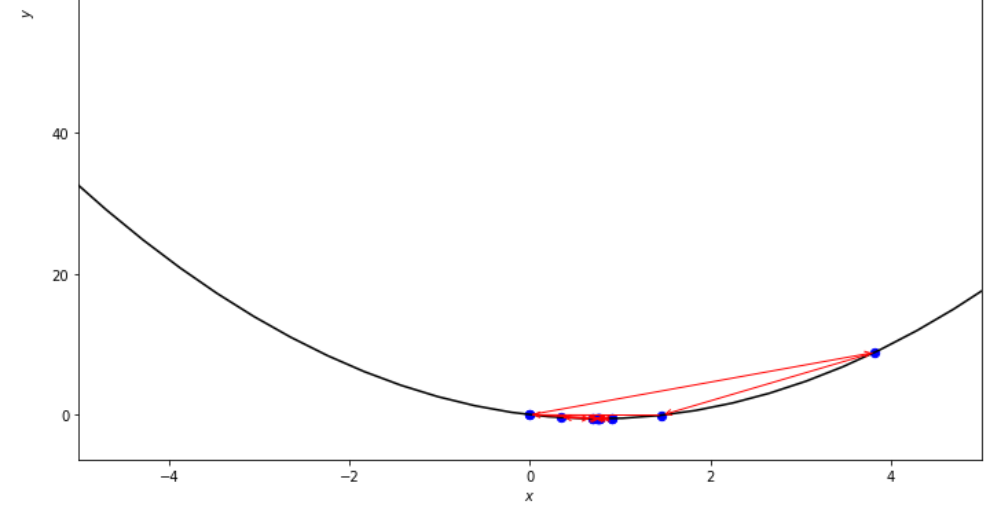
ลำดับของขั้นตอนที่ดำเนินการโดยอัลกอริทึม Fibonacci ก่อนถึงขั้นต่ำ
print ( 'x* =' , soom . golden_section ( f , xs , xf , epsilon ))
po2 . golden_section ( f , xs , xf , epsilon ) x* = 0.75 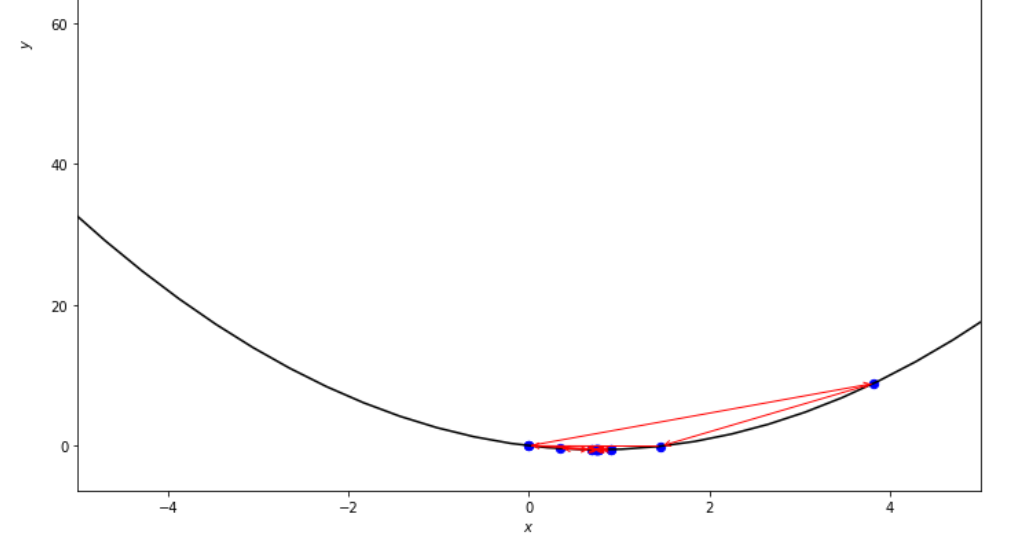
ลำดับของขั้นตอนที่ดำเนินการโดยอัลกอริทึมส่วนสีทองก่อนถึงขั้นต่ำ
ŋ = 2
xs = 100
print ( 'x* =' , soom . armijo_backward ( f , xs , ŋ , epsilon ))
po2 . armijo_backward ( f , xs , ŋ , epsilon ) x* = 0.78 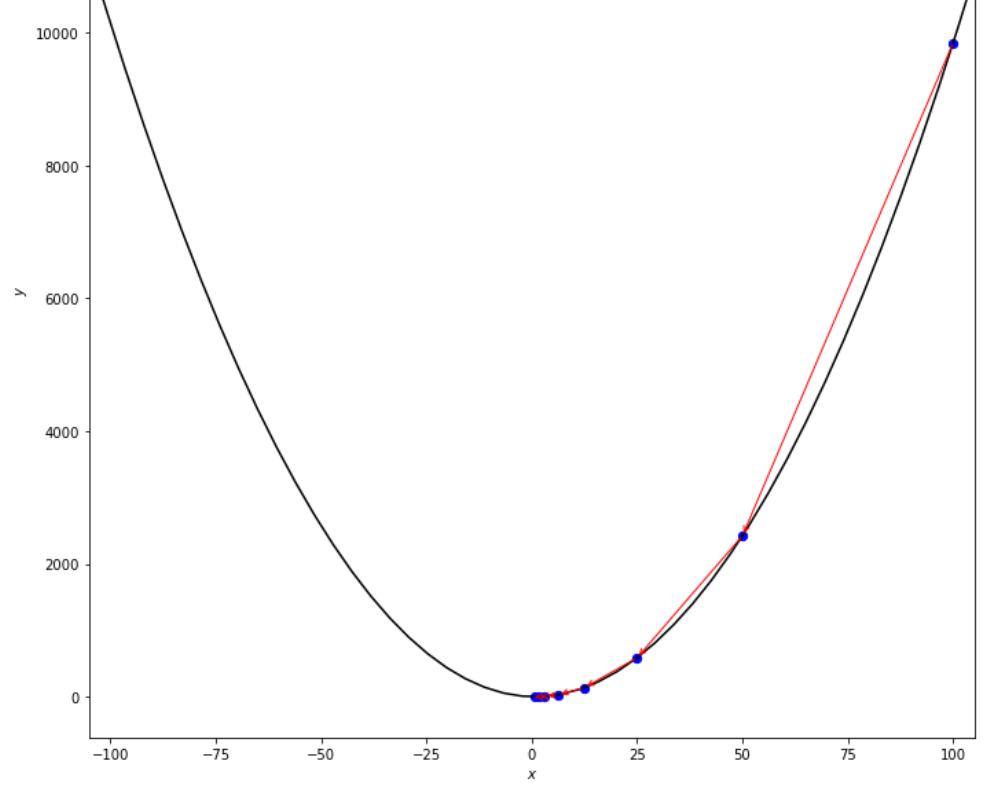
ลำดับของขั้นตอนที่ดำเนินการโดยอัลกอริทึม Armijo ย้อนหลังก่อนถึงขั้นต่ำ
xs = 0.1
epsilon = 0.5
ŋ = 2
print ( 'x* =' , soom . armijo_forward ( f , xs , ŋ , epsilon ))
po2 . armijo_forward ( f , xs , ŋ , epsilon ) x* = 0.8 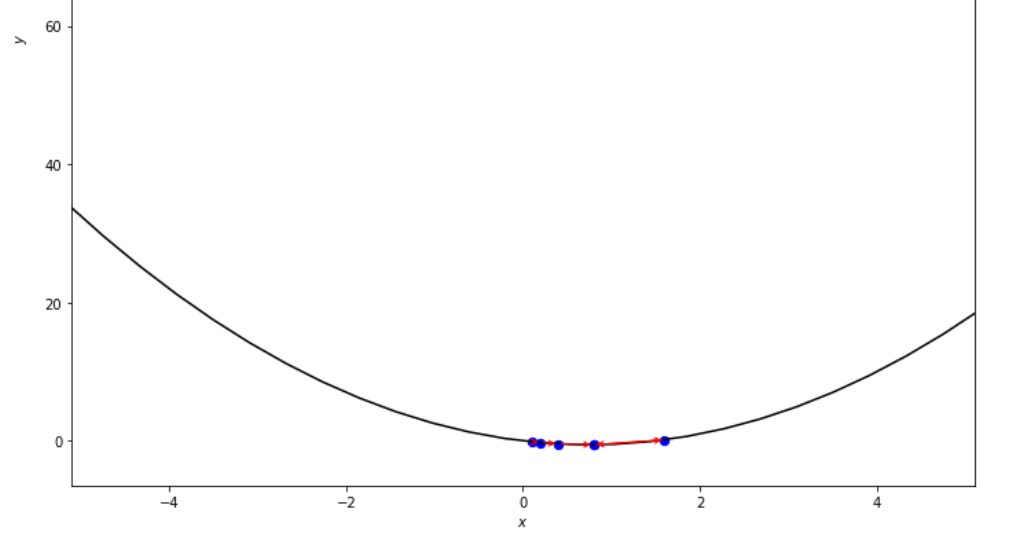
ลำดับของขั้นตอนที่ดำเนินการโดยอัลกอริทึมไปข้างหน้าของ Armijo ก่อนที่จะถึงขั้นต่ำ
po2 . compare_all_time ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 ) รันไทม์ 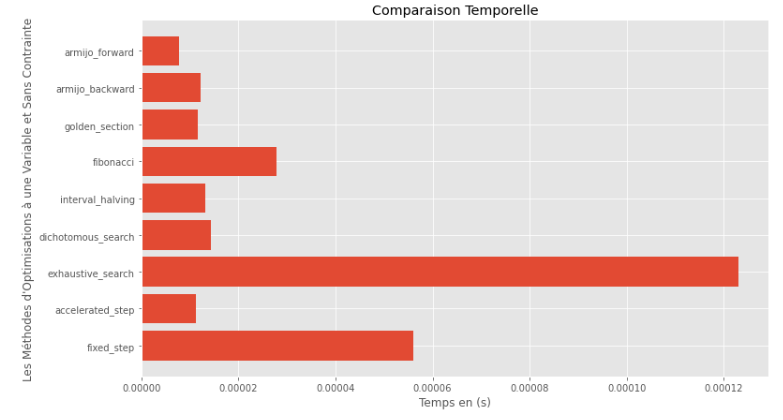
po2 . compare_all_precision ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 ) ช่องว่างระหว่างขั้นต่ำจริงและขั้นต่ำที่คำนวณ 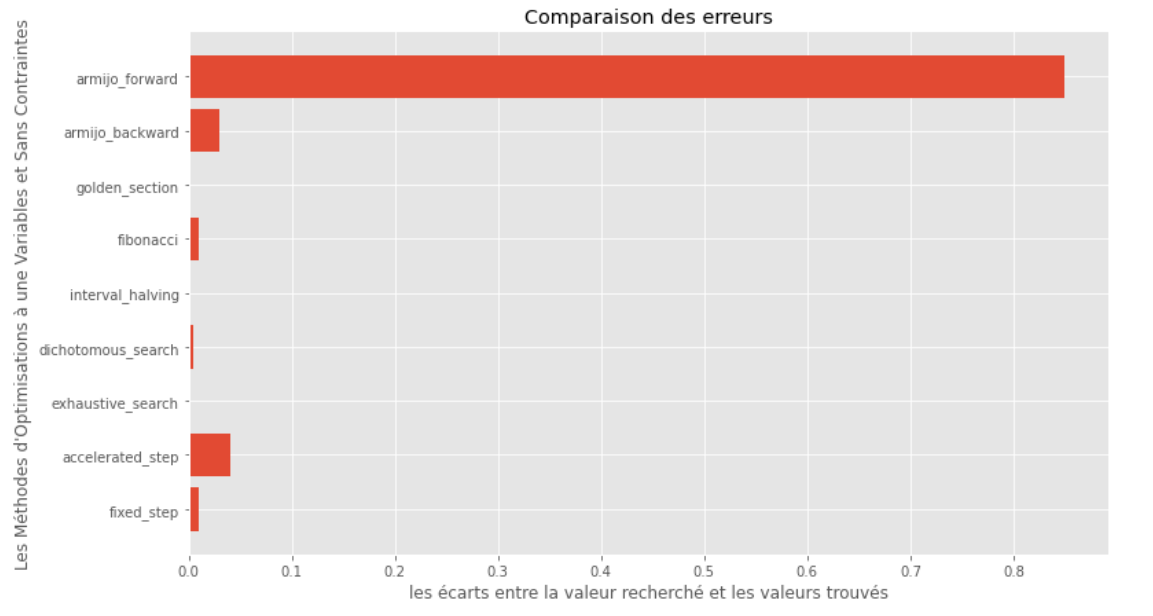
จากกราฟรันไทม์และความแม่นยำสามารถอนุมานได้ว่าในอัลกอริทึมที่ประเมินสำหรับฟังก์ชั่นตัวแปรเดี่ยวนูนนี้วิธี การส่วนสีทอง นั้นเป็นตัวเลือกที่ดีที่สุดโดยเสนอการผสมผสานของความแม่นยำสูง
import pyoptim . my_plot . multivar . _3D as pm3
import pyoptim . my_plot . multivar . contour2D as pmc def h ( x ):
return x [ 0 ] - x [ 1 ] + 2 * ( x [ 0 ] ** 2 ) + 2 * x [ 1 ] * x [ 0 ] + x [ 1 ] ** 2
# analytically, argmin(f) = [-1, 1.5]วิธีแก้ปัญหาทางทวารหนัก
X = [ 1000 , 897 ]
alpha = 1.e-2
tol = 1.e-2 pmc . gradient_descent ( h , X , tol , alpha )
pm3 . gradient_descent ( h , X , tol , alpha ) Y* = [-1.01 1.51] ลำดับของขั้นตอนที่ดำเนินการโดยอัลกอริทึมการไล่ระดับสีก่อนที่จะถึงขั้นต่ำ 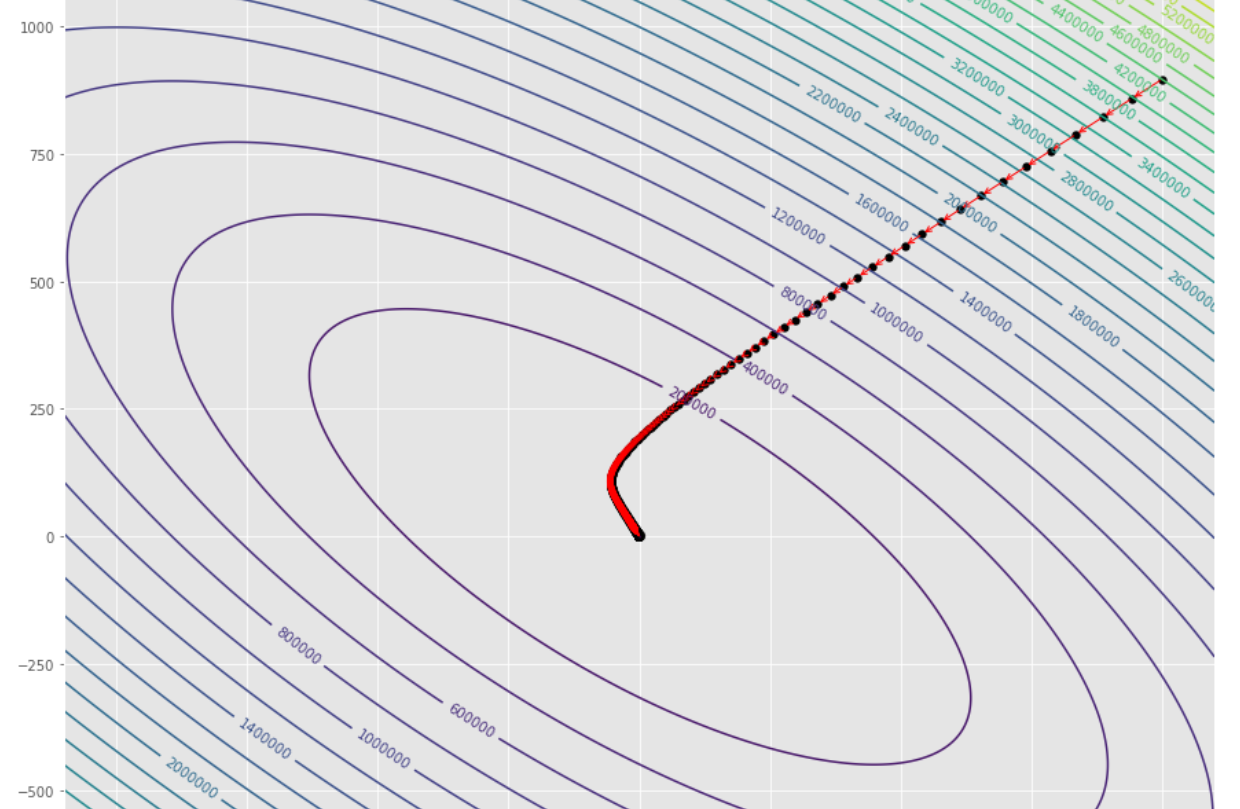
พล็อตรูปร่าง 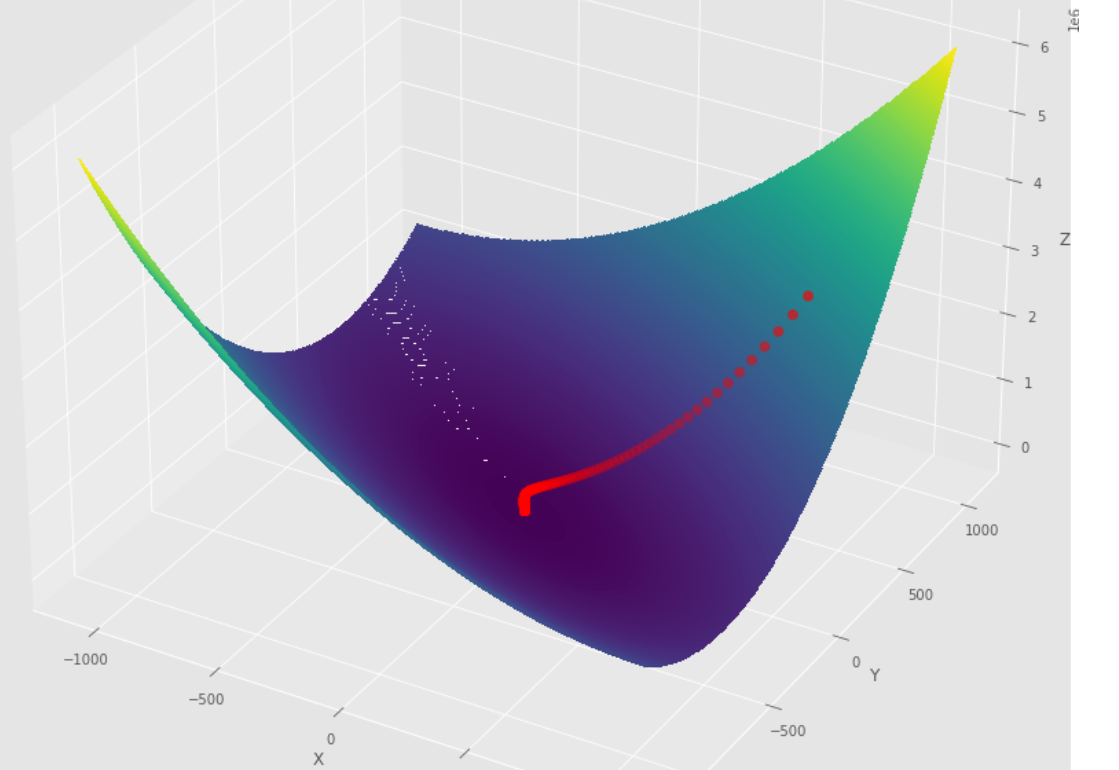
พล็อต 3 มิติ
pmc . gradient_conjugate ( h , X , tol )
pm3 . gradient_conjugate ( h , X , tol ) Y* = [-107.38 172.18] ลำดับของขั้นตอนที่ดำเนินการโดยอัลกอริทึมการไล่ระดับสีคอนจูเกตก่อนถึงขั้นต่ำ 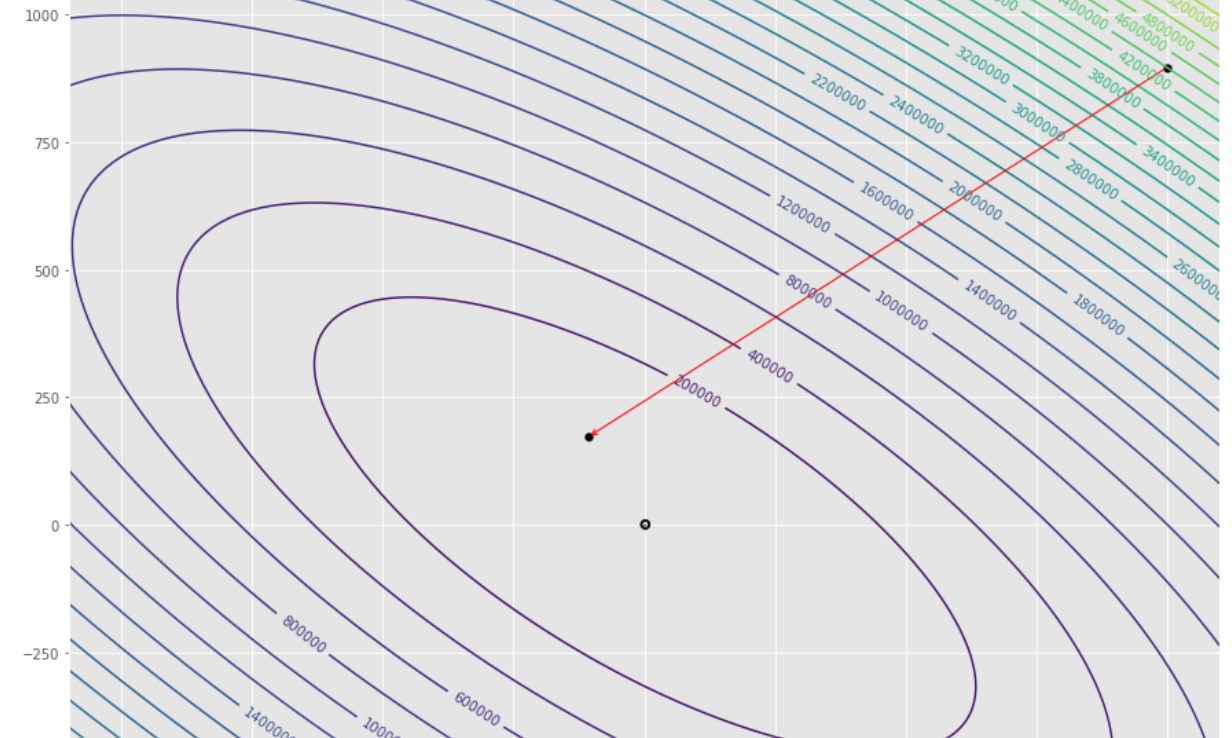
พล็อตรูปร่าง 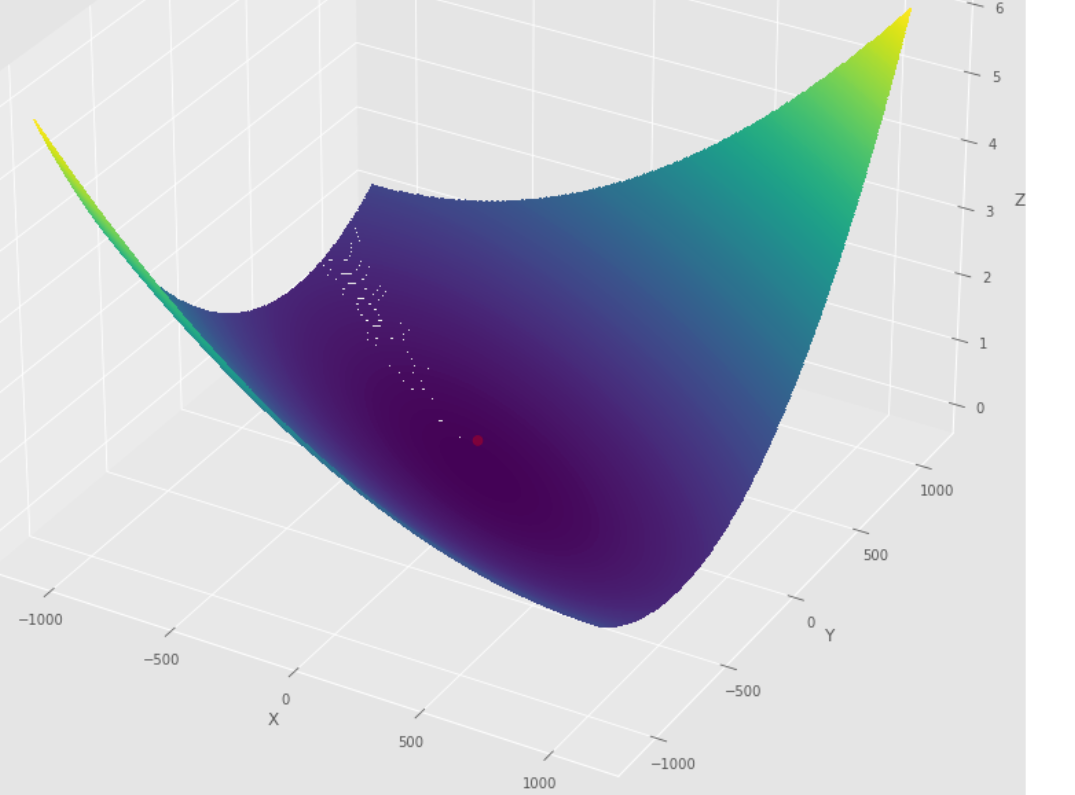
พล็อต 3 มิติ
pmc . newton ( h , X , tol )
pm3 . newton ( h , X , tol ) Y* = [-1. 1.5] ลำดับของขั้นตอนที่ดำเนินการโดยอัลกอริทึมนิวตันก่อนถึงขั้นต่ำ 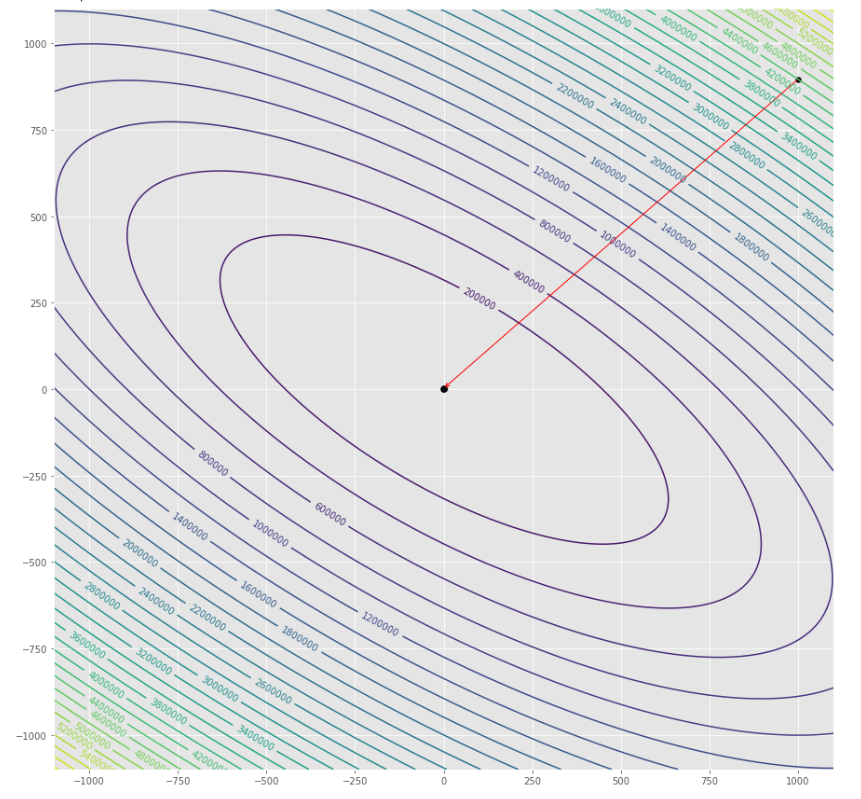
พล็อตรูปร่าง 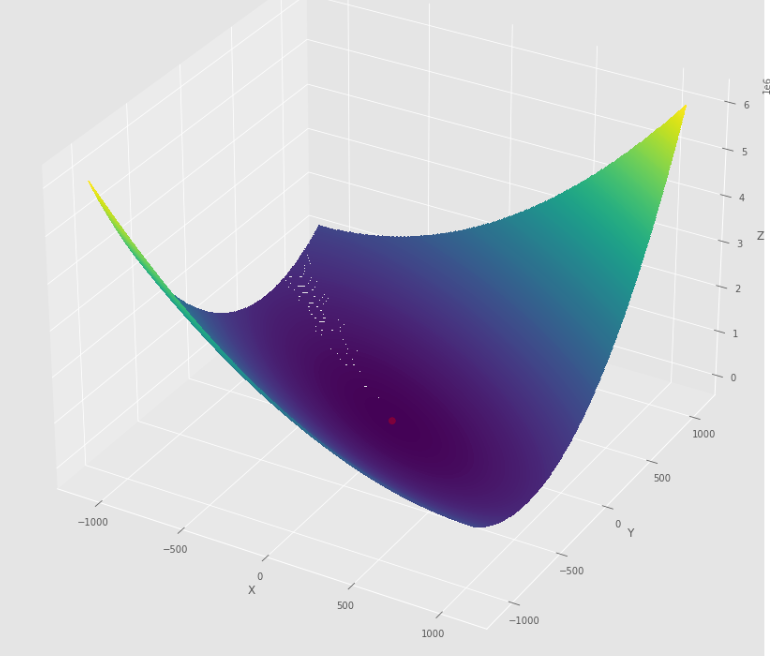
พล็อต 3 มิติ
pmc . quasi_newton_dfp ( h , X , tol )
pm3 . quasi_newton_dfp ( h , X , tol ) Y* = [-1. 1.5] ลำดับของขั้นตอนที่ดำเนินการโดยอัลกอริทึม quasi Newton DFP ก่อนถึงขั้นต่ำ 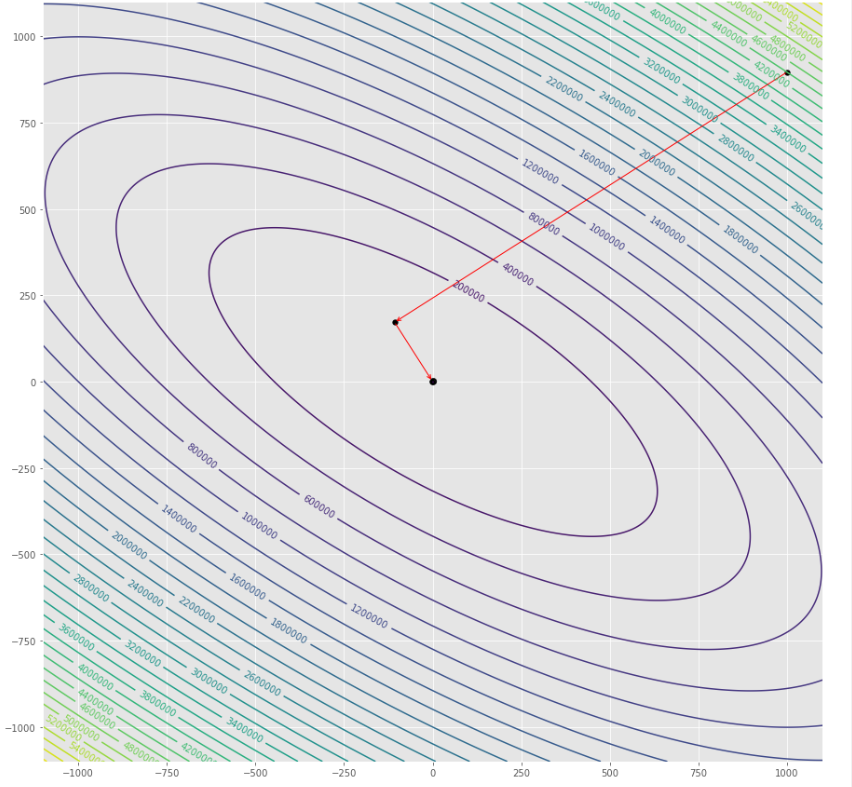
พล็อตรูปร่าง 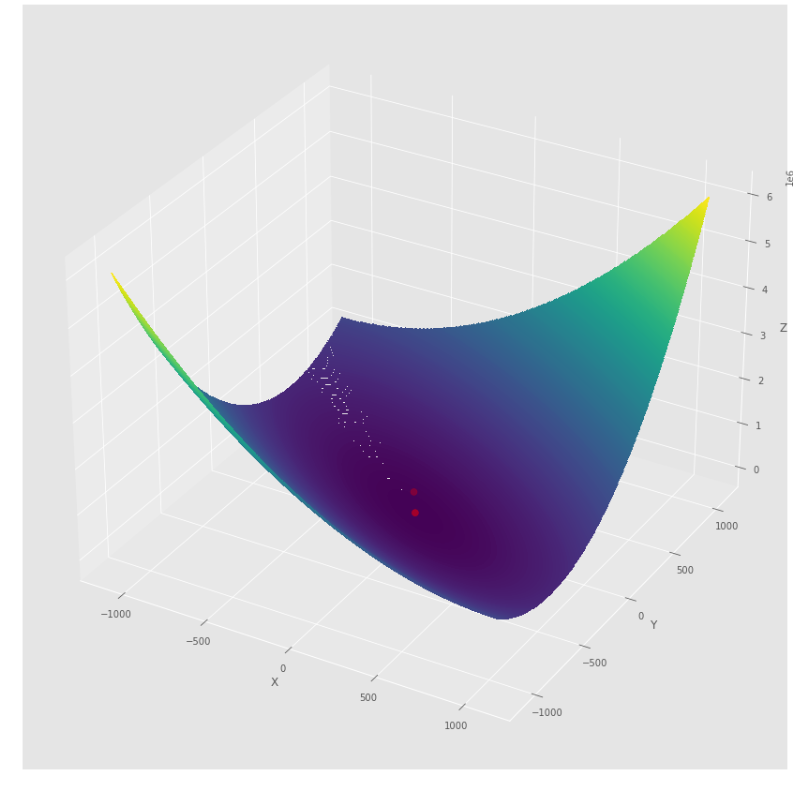
พล็อต 3 มิติ
pmc . sgd ( h , X , tol , alpha )
pm3 . sgd ( h , X , tol , alpha ) Y* = [-1.01 1.52] ลำดับของขั้นตอนที่ดำเนินการโดยอัลกอริทึมการไล่ระดับสีแบบสุ่มก่อนที่จะถึงขั้นต่ำ 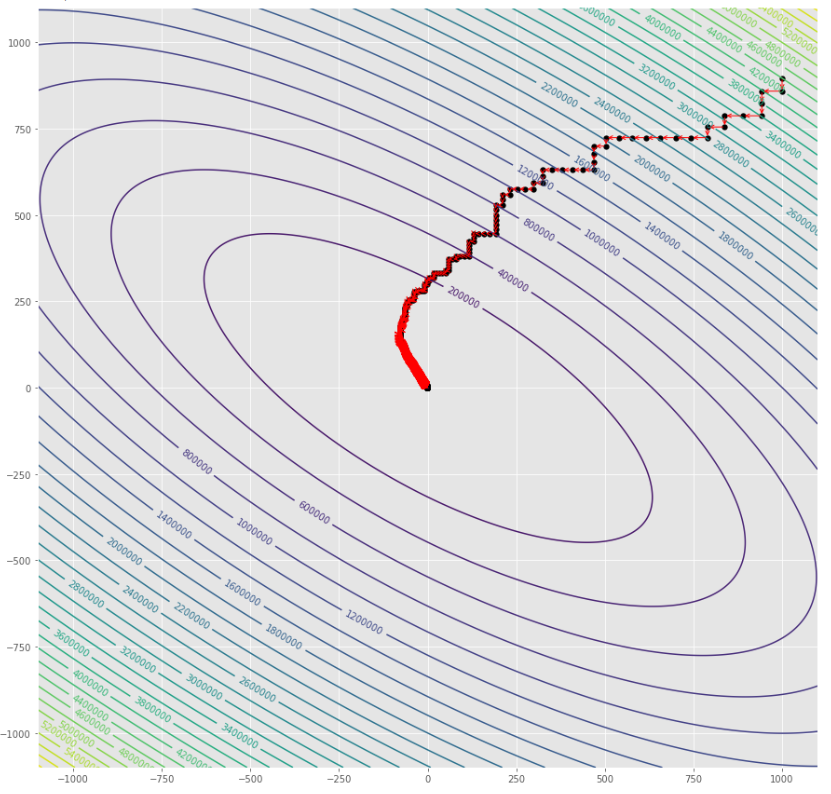
พล็อตรูปร่าง 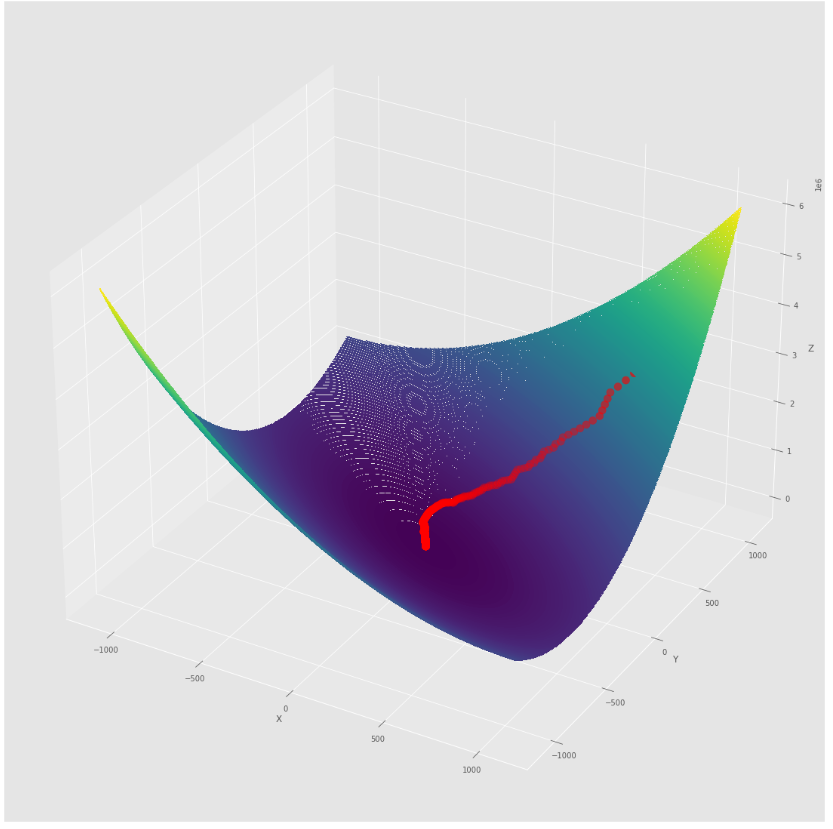
พล็อต 3 มิติ
alpha = 100 #it must be high because of BLS
c = 2
pmc . sgd_with_bls ( h , X , tol , alpha , c )
pm3 . sgd_with_bls ( h , X , tol , alpha , c ) Y* = [-1. 1.5] ลำดับของขั้นตอนที่ดำเนินการโดยการไล่ระดับสีแบบสุ่มด้วยอัลกอริทึม BLS ก่อนถึงขั้นต่ำ 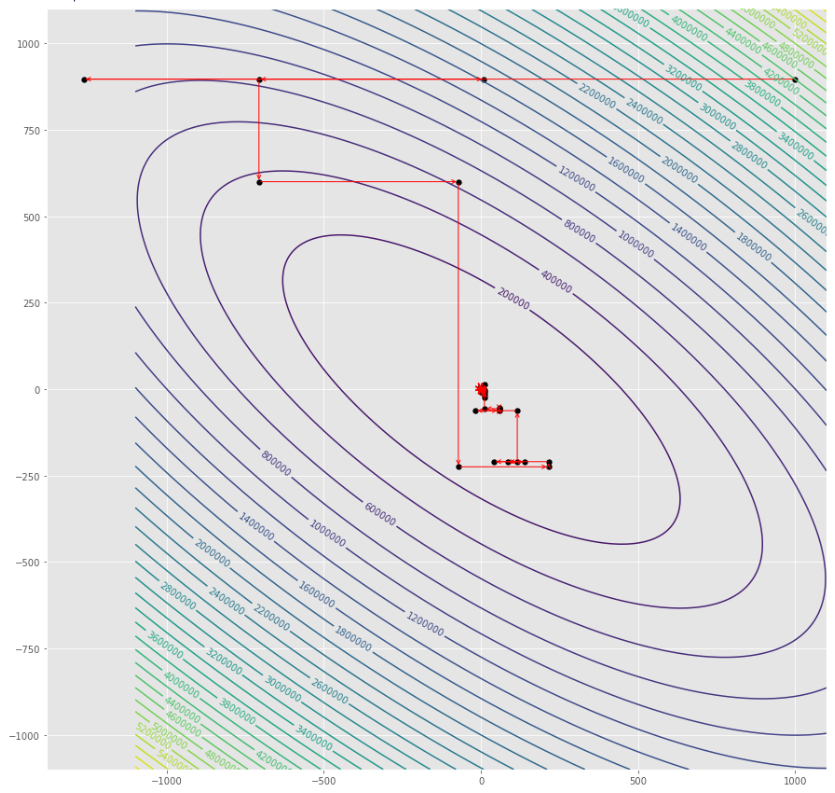
พล็อตรูปร่าง 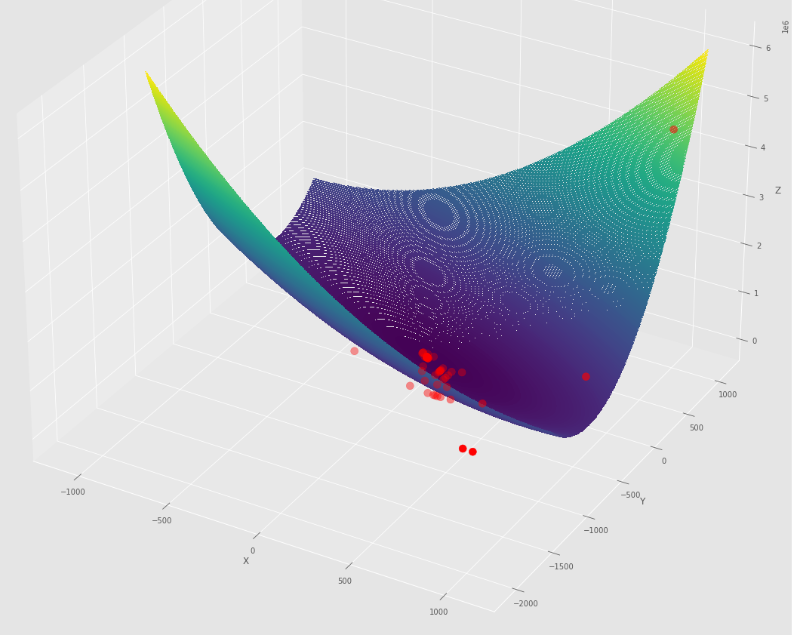
พล็อต 3 มิติ
pm3 . compare_all_time ( h , X , 1.e-2 , 1.e-1 , 100 , 2 ) รันไทม์ 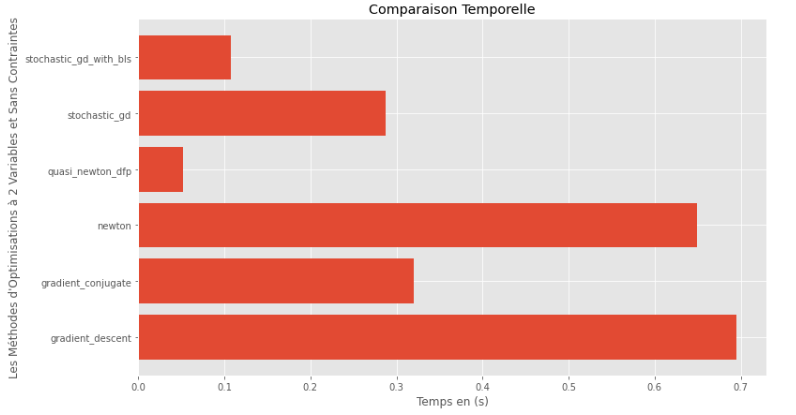
pm3 . compare_all_precision ( h , X , 1.e-2 , 1.e-1 , 100 , 2 ) ช่องว่างระหว่างขั้นต่ำจริงและขั้นต่ำที่คำนวณ 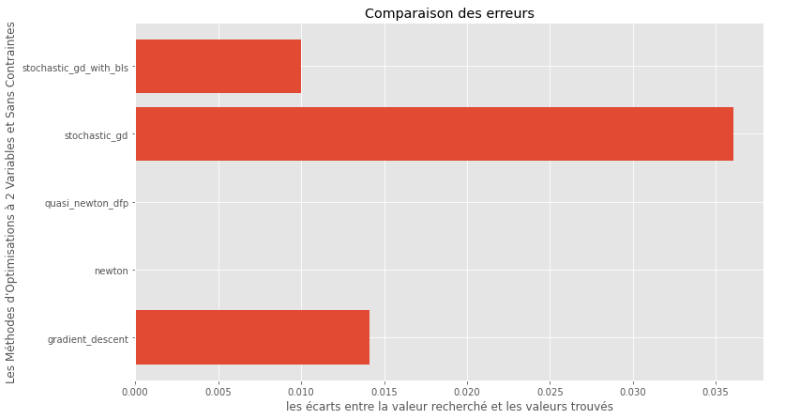
จากกราฟรันไทม์และความแม่นยำสามารถอนุมานได้ว่าในอัลกอริทึมที่ประเมินสำหรับฟังก์ชั่นหลายตัวแปรนูนนี้วิธี กึ่งนิวตัน DFP นั้นเป็นตัวเลือกที่ดีที่สุด
import pyoptim . my_numpy . inverse as npi 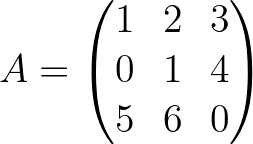
A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]]) A_1 = npi . gaussjordan ( A . copy ())
I = A @ A_1
I = np . around ( I , 1 )
print ( 'A_1 = n n ' , A_1 )
print ( ' n A_1*A = n n ' , I ) A_1 =
[[-24. 18. 5.]
[ 20. -15. -4.]
[ -5. 4. 1.]]
A_1*A =
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]] import pyoptim . my_numpy . decompose as npd A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]]) #A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ],[ - 1. , 2. , - 1. ],[ 0. , - 1. , 2. ]]) #B is positive definite
Y = np . array ([ 45 , - 78 , 95 ]) #randomly chosen column vector L , U , P = npd . LU ( A )
print ( "P = n " , P , " n n L = n " , L , " n n U = n " , U )
print ( " n " , A == P @ L @ U ) P =
[[0. 0. 1.]
[0. 1. 0.]
[1. 0. 0.]]
L =
[[1. 0. 0. ]
[0. 1. 0. ]
[0.2 0.8 1. ]]
U =
[[ 5. 6. 0. ]
[ 0. 1. 4. ]
[ 0. 0. -0.2]]
[[ True True True]
[ True True True]
[ True True True]] L = npd . choleski ( A ) # A is not positive definite
print ( L )
print ( "--------------------------------------------------" )
L = npd . choleski ( B ) # B is positive definite
print ( 'L = n ' , L , ' n ' )
C = np . around ( L @( L . T ), 1 )
print ( 'B = L@(L.T) n n ' , B == C ) A must be positive definite !
None
--------------------------------------------------
L =
[[ 1.41421356 0. 0. ]
[-0.70710678 1.22474487 0. ]
[ 0. -0.81649658 1.15470054]]
B = L@(L.T)
[[ True True True]
[ True True True]
[ True True True]] import pyoptim . my_numpy . solve as nps 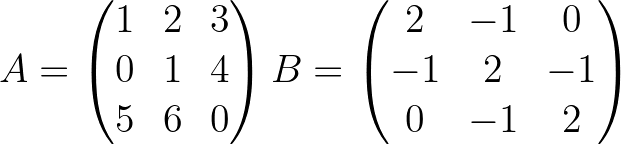
A = np . array ([[ 1. , 2. , 3. ], [ 0. , 1. , 4. ], [ 5. , 6. , 0. ]]) # A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ], [ - 1. , 2. , - 1. ], [ 0. , - 1. , 2. ]]) # B is positive definite
Y = np . array ([ 45 , - 78 , 95 ]) # randomly chosen column vector X = nps . gaussjordan ( A , Y )
print ( "X = n " , X )
print ( " n A@X=Y n " , A @ X == Y , ' n ' )
print ( '---------------------------------------------------------------' )
X = nps . gaussjordan ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n B@X=Y n " , Y_ == Y , ' n ' ) X =
[[-2009.]
[ 1690.]
[ -442.]]
A@X=Y
[[ True]
[ True]
[ True]]
---------------------------------------------------------------
X =
[[18.5]
[-8. ]
[43.5]]
B@X=Y
[[ True]
[ True]
[ True]]
X = nps . LU ( A , Y )
print ( "X* = n " , X )
print ( " n AX*=Y n " , A @ X == Y )
print ( "-------------------------------------------------------------------------------" );
X = nps . LU ( B , Y )
print ( "X* = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y ) X* =
[[-2009.]
[ 1690.]
[ -442.]]
AX*=Y
[[ True]
[ True]
[ True]]
-------------------------------------------------------------------------------
X* =
[[18.5]
[-8. ]
[43.5]]
BX*=Y
[[ True]
[ True]
[ True]] X = nps . choleski ( A , Y )
print ( "-------------------------------------------------------------------------------" )
X = nps . choleski ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y ) !! A must be positive definite !!
-------------------------------------------------------------------------------
X =
[[18.5]
[-8. ]
[43.5]]
BX*=Y
[[ True]
[ True]
[ True]]