Pyoptim: package python pour les opérations d'optimisation et de matrice
Ce projet, une composante du cours d'analyse et d'optimisation numérique à ESIAS, Mohammed V University est né de la suggestion du professeur M. Naoum de créer un package Python encapsulant des algorithmes pratiqués pendant les séances de laboratoire. Il se concentre sur environ dix algorithmes d'optimisation non contraints, offrant des visualisations 2D et 3D, permettant une comparaison de performances en efficacité et précision de calcul. De plus, le projet englobe les opérations matricielles telles que l'inversion, la décomposition et la résolution de systèmes linéaires, tous intégrés dans le package contenant les algorithmes dérivés de laboratoire.
GIF Source: https://www.nsf.gov/news/mmg/mmg_disp.jsp?med_id=78950&from=
Chaque partie de ce projet est un exemple de code qui montre comment faire ce qui suit:
Implémentation d'algorithmes d'optimisation à une variable, englobant FIXT_STEP, accéléré_step, exhaustif_search, dichotomous_search, interval_halving, fibonacci, golden_section, armijo_backward et armijo_forward.
Incorporation de divers algorithmes d'optimisation à une variable, y compris la descente de gradient, le conjugué de gradient, Newton, Quasi_newton_DFP, une descente de gradient stochastique.
Visualisation de chaque étape d'itération pour tous les algorithmes dans les formats 2D, contour et 3D.
Effectuer une analyse comparative axée sur leurs mesures d'exécution et de précision.
Mise en œuvre d'opérations matricielles telles que l'inversion (par exemple, Gauss-Jordan), la décomposition (par exemple, Lu, Choleski) et les solutions pour les systèmes linéaires (par exemple, Gauss-Jordan, Lu, Choleski).
Pour installer ce package Python:
pip install pyoptimExécutez ce cahier de démonstration
import pyoptim . my_scipy . onevar_optimize . minimize as soom
import pyoptim . my_plot . onevar . _2D as po2 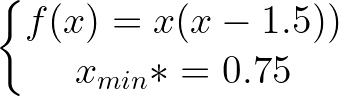
def f ( x ):
return x * ( x - 1.5 ) # analytically, argmin(f) = 0.75 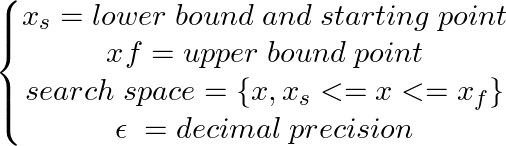
xs = - 10
xf = 10
epsilon = 1.e-2 print ( 'x* =' , soom . fixed_step ( f , xs , epsilon ))
po2 . fixed_step ( f , xs , epsilon ) x* = 0.75 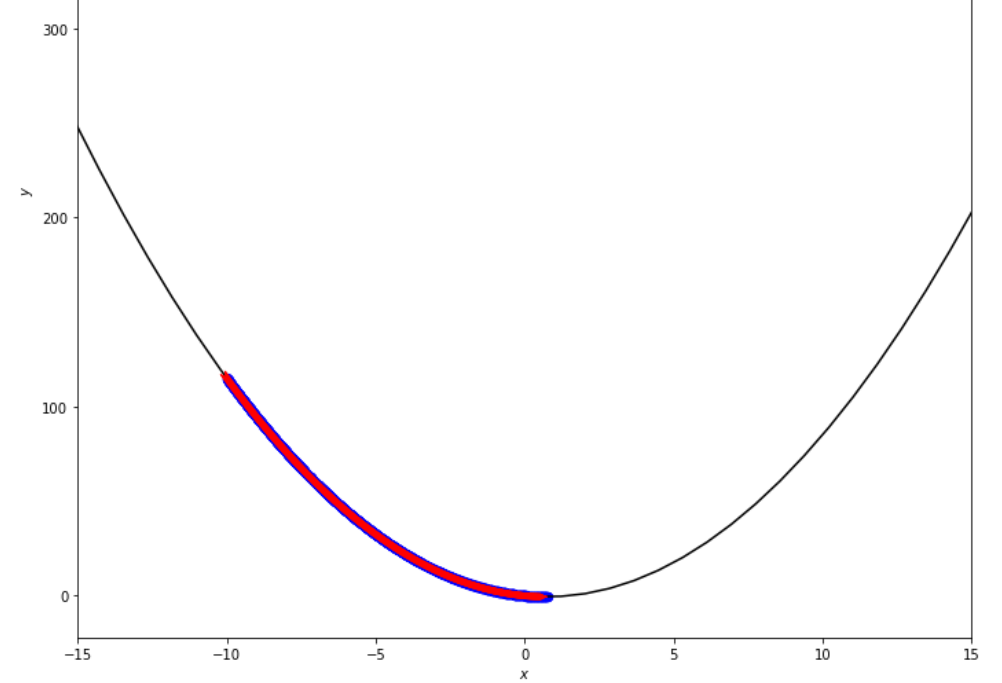
La séquence des étapes prises par l'algorithme de pas fixes avant d'atteindre le minimum
print ( 'x* =' , soom . accelerated_step ( f , xs , epsilon ))
po2 . accelerated_step ( f , xs , epsilon ) x* = 0.86 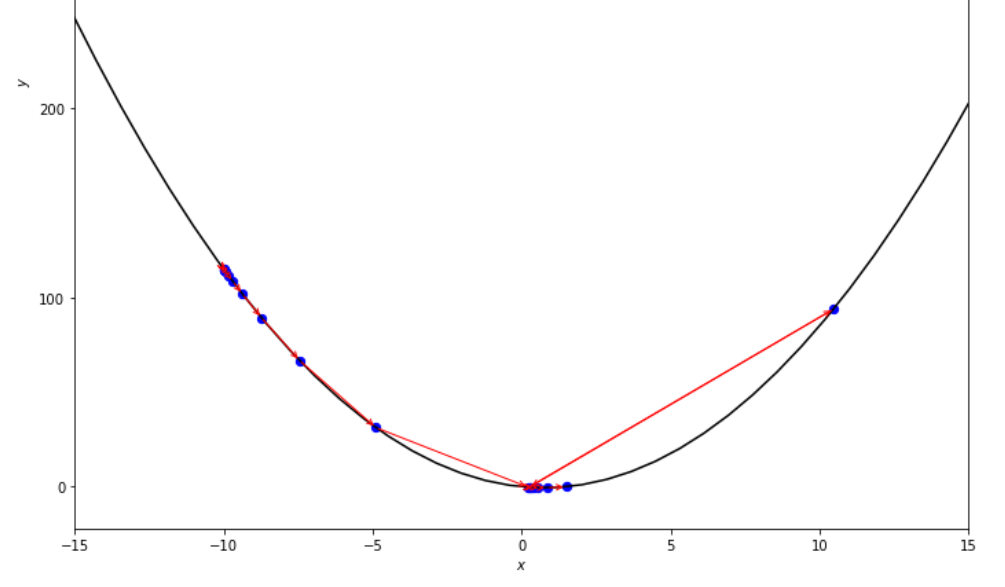
La séquence des étapes prises par l'algorithme de pas accéléré avant d'atteindre le minimum
print ( 'x* =' , soom . exhaustive_search ( f , xs , xf , epsilon ))
po2 . exhaustive_search ( f , xs , xf , epsilon ) x* = 0.75
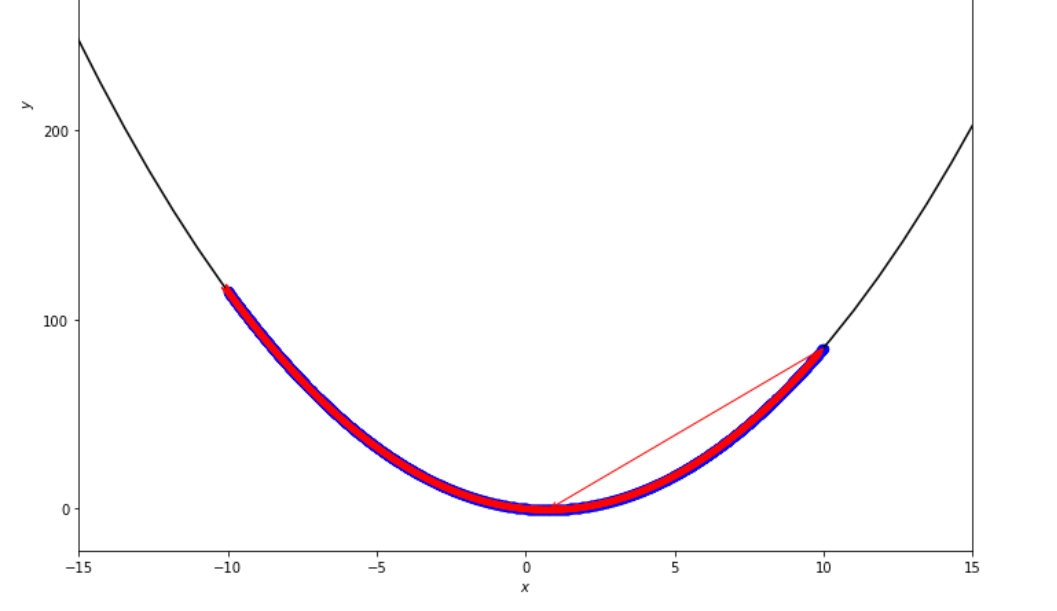
La séquence des étapes prises par l'algorithme de recherche exhaustif avant d'atteindre le minimum
mini_delta = 1.e-3
print ( 'x* =' , soom . dichotomous_search ( f , xs , xf , epsilon , mini_delta ))
po2 . dichotomous_search ( f , xs , xf , epsilon , mini_delta ) x* = 0.7494742431640624
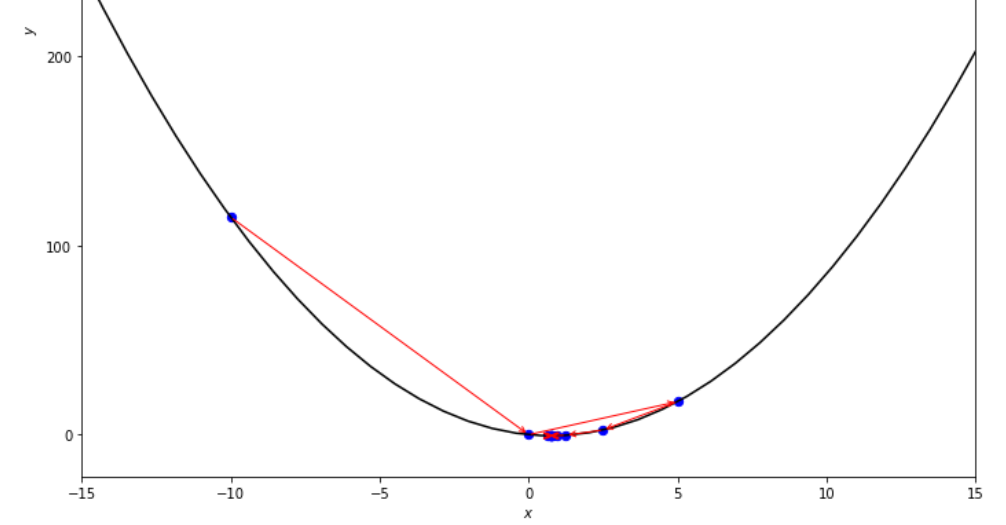
La séquence des étapes prises par l'algorithme de recherche dichotomique avant d'atteindre le minimum
print ( 'x* =' , soom . interval_halving ( f , xs , xf , epsilon ))
po2 . interval_halving ( f , xs , xf , epsilon ) x* = 0.75
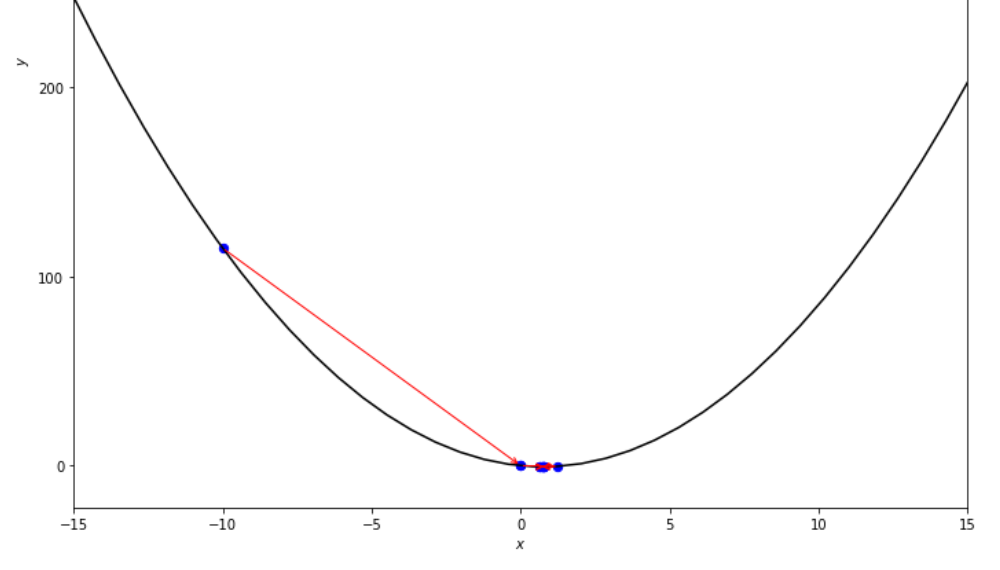
La séquence des étapes prises par l'algorithme de réduction d'intervalle avant d'atteindre le minimum.
n = 15
print ( 'x* =' , soom . fibonacci ( f , xs , xf , n ))
po2 . fibonacci ( f , xs , xf , n ) x* = 0.76 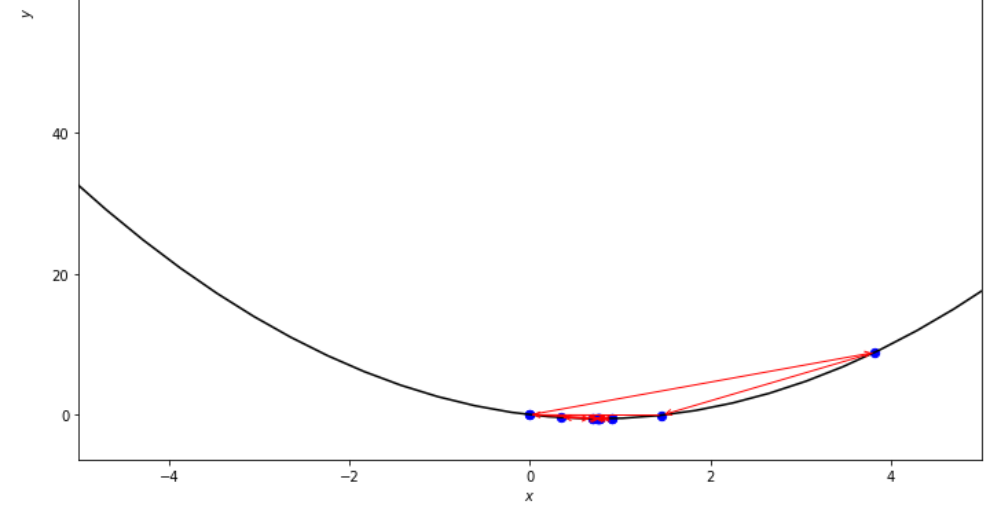
La séquence des étapes prises par l'algorithme Fibonacci avant d'atteindre le minimum.
print ( 'x* =' , soom . golden_section ( f , xs , xf , epsilon ))
po2 . golden_section ( f , xs , xf , epsilon ) x* = 0.75 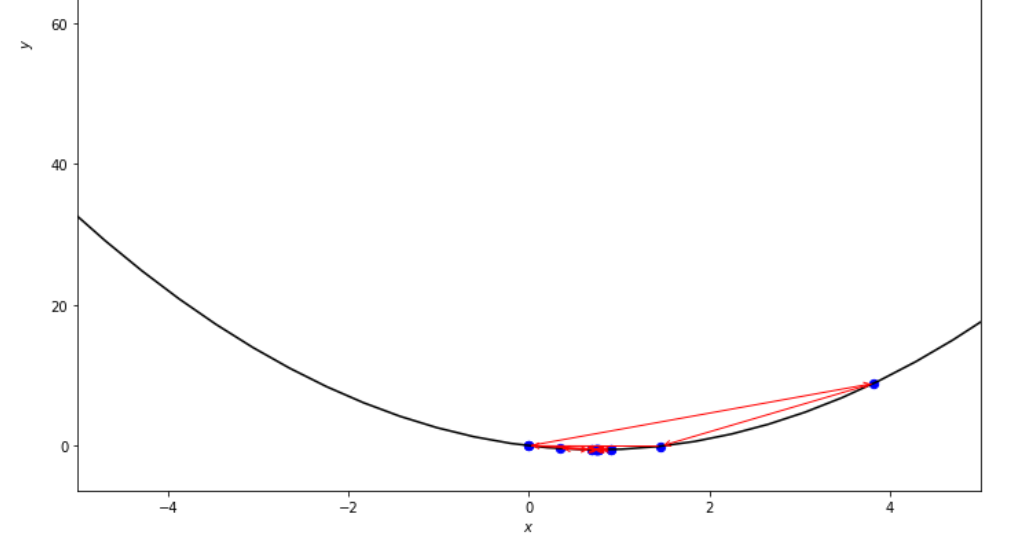
La séquence des étapes prises par l'algorithme de section dorée avant d'atteindre le minimum
ŋ = 2
xs = 100
print ( 'x* =' , soom . armijo_backward ( f , xs , ŋ , epsilon ))
po2 . armijo_backward ( f , xs , ŋ , epsilon ) x* = 0.78 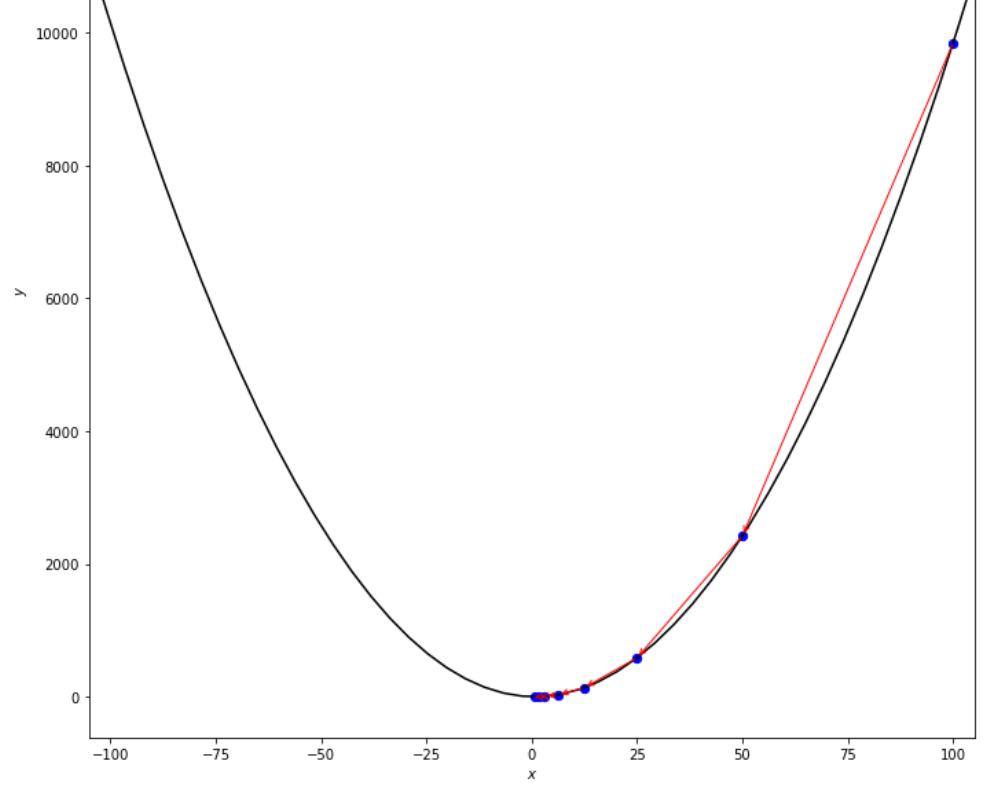
La séquence des étapes prises par l'algorithme d'arrière Armijo avant d'atteindre le minimum
xs = 0.1
epsilon = 0.5
ŋ = 2
print ( 'x* =' , soom . armijo_forward ( f , xs , ŋ , epsilon ))
po2 . armijo_forward ( f , xs , ŋ , epsilon ) x* = 0.8 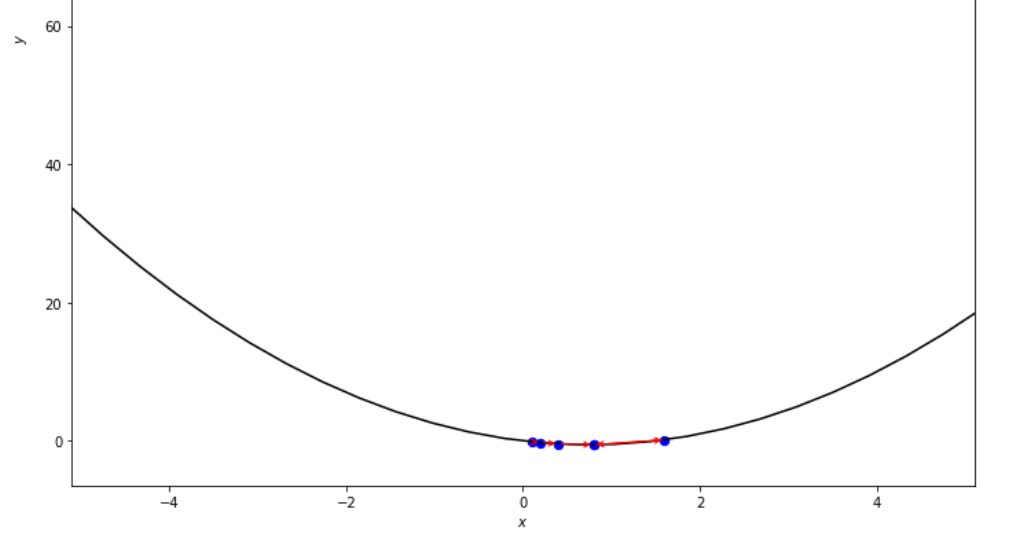
La séquence des étapes prises par l'algorithme avant ARMIJO avant d'atteindre le minimum
po2 . compare_all_time ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 ) Temps d'exécution 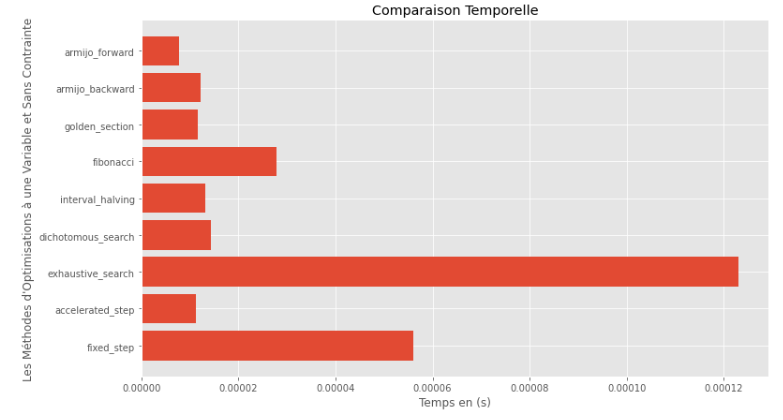
po2 . compare_all_precision ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 ) Écart entre le minimum vrai et calculé 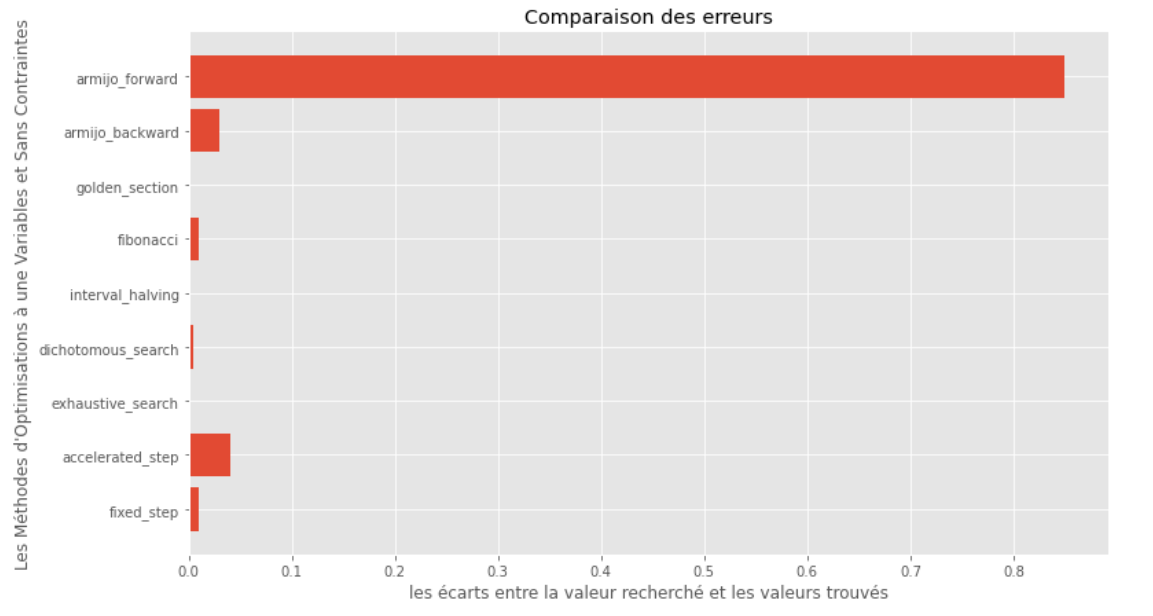
D'après les graphiques d'exécution et de précision, on peut en déduire que parmi les algorithmes évalués pour cette fonction convexe à variable unique, la méthode de la section dorée apparaît comme le choix optimal, offrant un mélange de haute précision et notamment de l'exécution faible.
import pyoptim . my_plot . multivar . _3D as pm3
import pyoptim . my_plot . multivar . contour2D as pmc def h ( x ):
return x [ 0 ] - x [ 1 ] + 2 * ( x [ 0 ] ** 2 ) + 2 * x [ 1 ] * x [ 0 ] + x [ 1 ] ** 2
# analytically, argmin(f) = [-1, 1.5]solution analogique
X = [ 1000 , 897 ]
alpha = 1.e-2
tol = 1.e-2 pmc . gradient_descent ( h , X , tol , alpha )
pm3 . gradient_descent ( h , X , tol , alpha ) Y* = [-1.01 1.51] La séquence des étapes prises par l'algorithme de descente de gradient avant d'atteindre le minimum 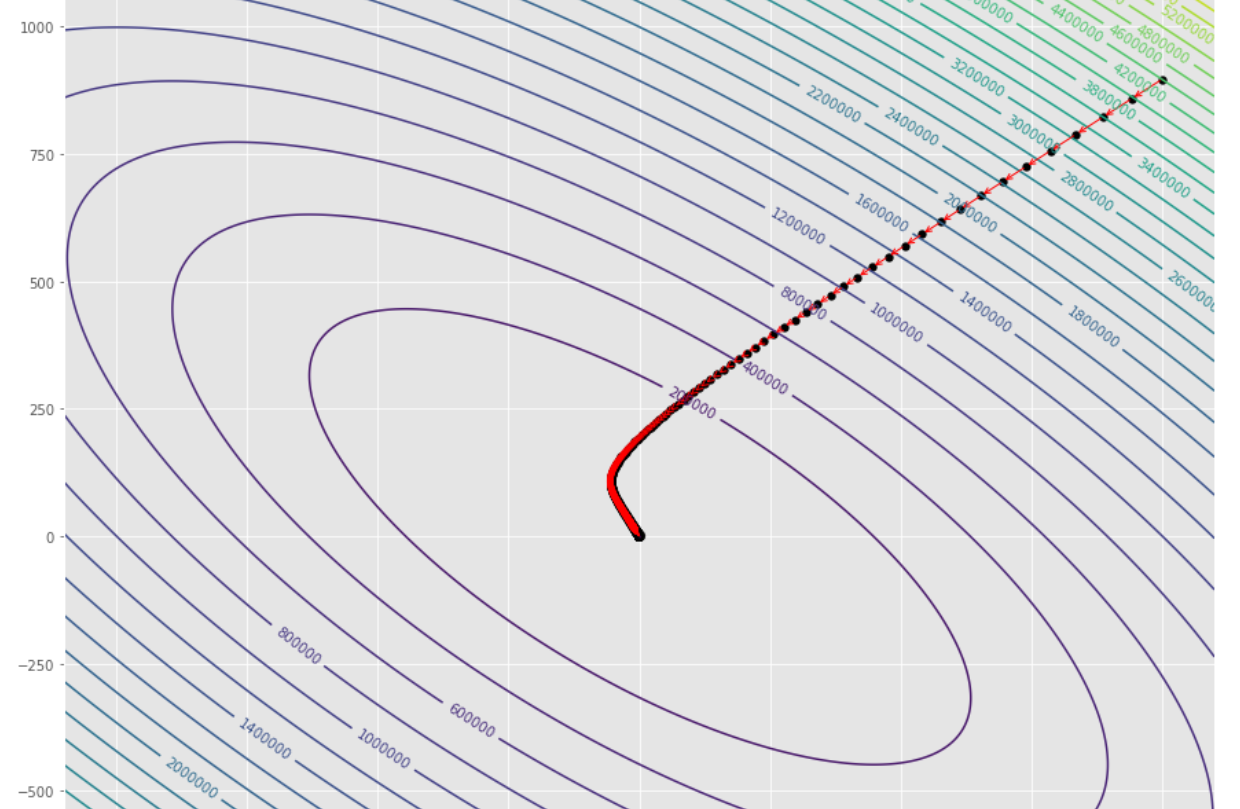
Tracé de contour 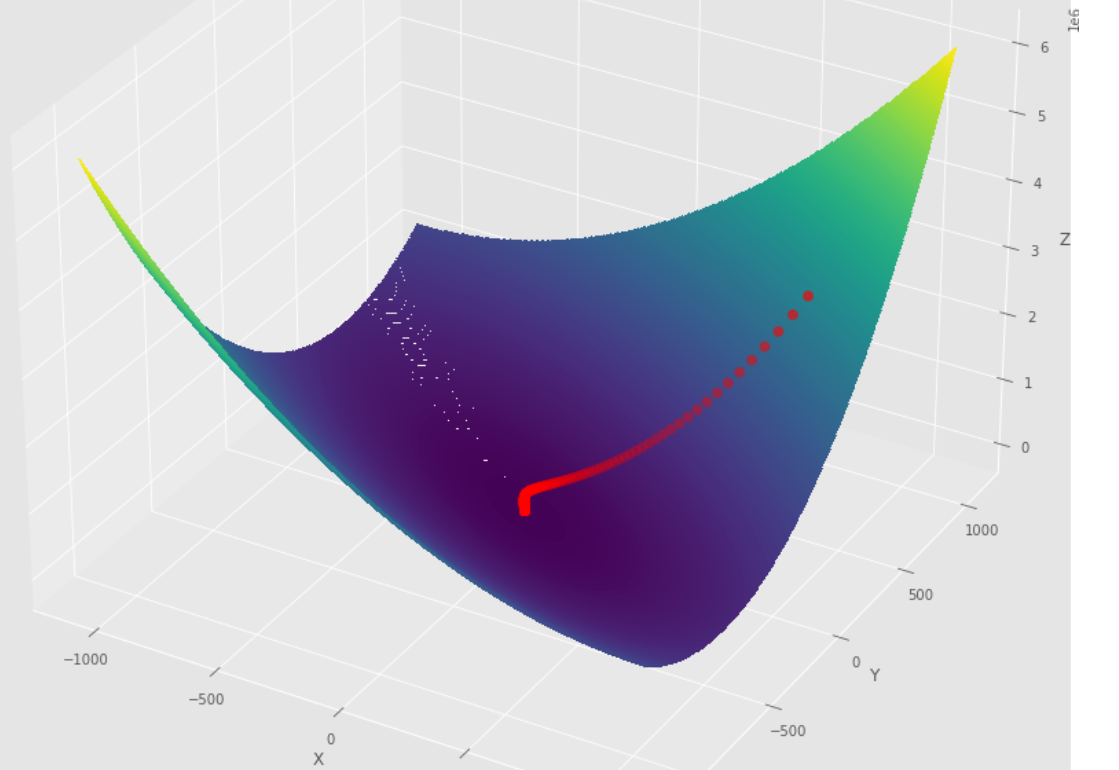
Terrain 3D
pmc . gradient_conjugate ( h , X , tol )
pm3 . gradient_conjugate ( h , X , tol ) Y* = [-107.38 172.18] La séquence des étapes prises par l'algorithme de conjugué de gradient avant d'atteindre le minimum 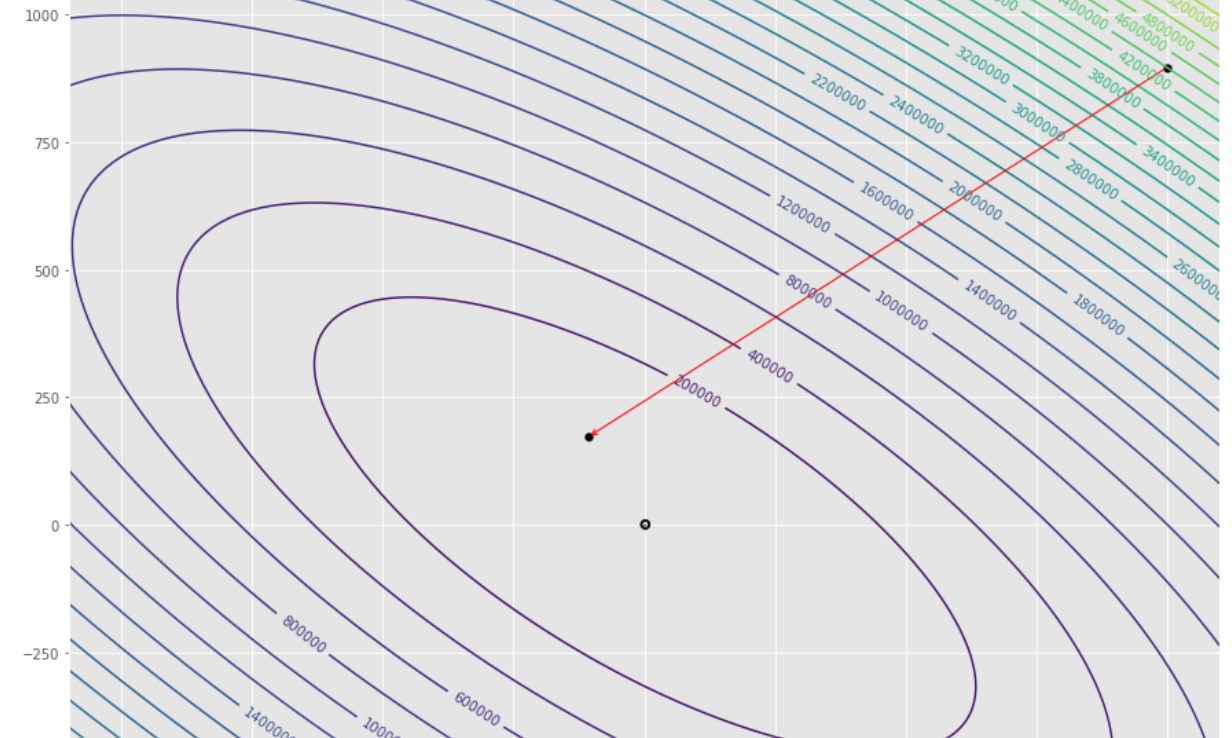
Tracé de contour 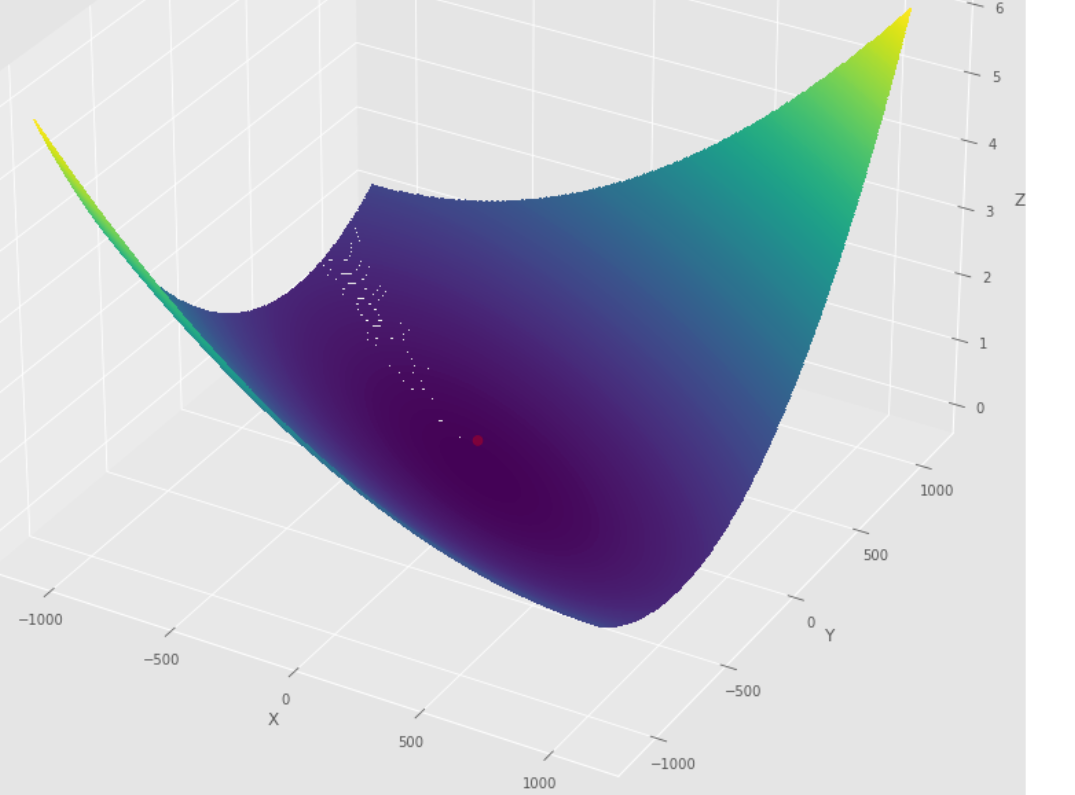
Terrain 3D
pmc . newton ( h , X , tol )
pm3 . newton ( h , X , tol ) Y* = [-1. 1.5] La séquence de mesures prises par l'algorithme de Newton avant d'atteindre le minimum 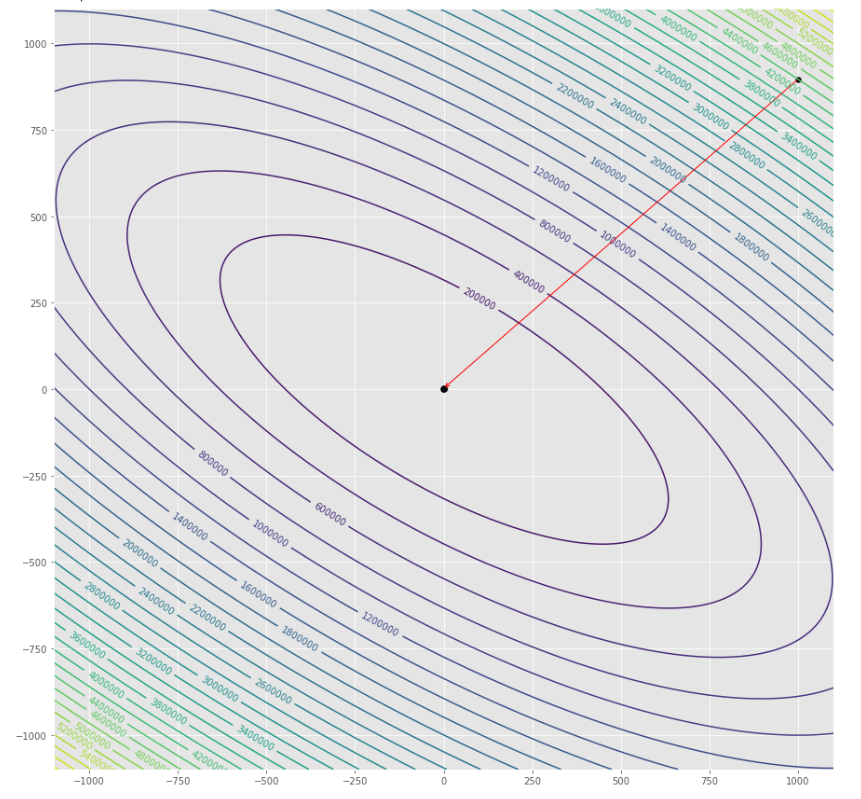
Tracé de contour 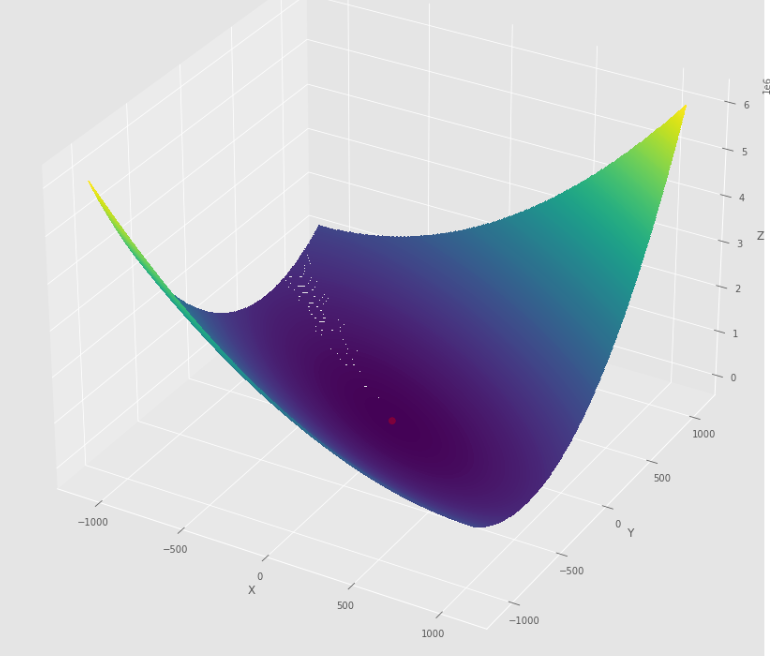
Terrain 3D
pmc . quasi_newton_dfp ( h , X , tol )
pm3 . quasi_newton_dfp ( h , X , tol ) Y* = [-1. 1.5] La séquence des étapes prises par l'algorithme DFP Quasi Newton avant d'atteindre le minimum 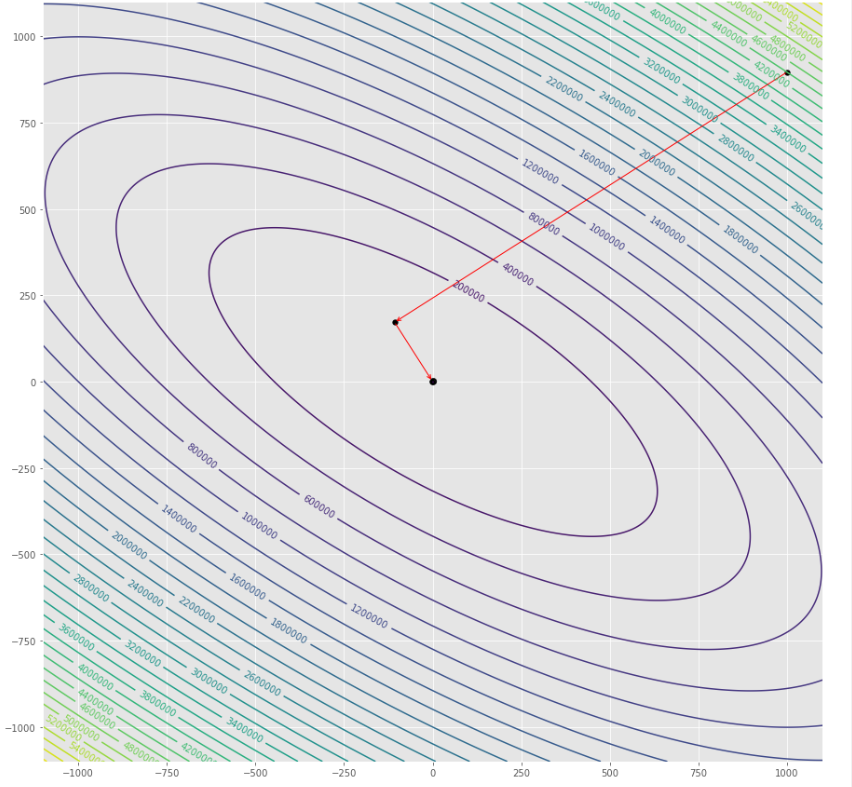
Tracé de contour 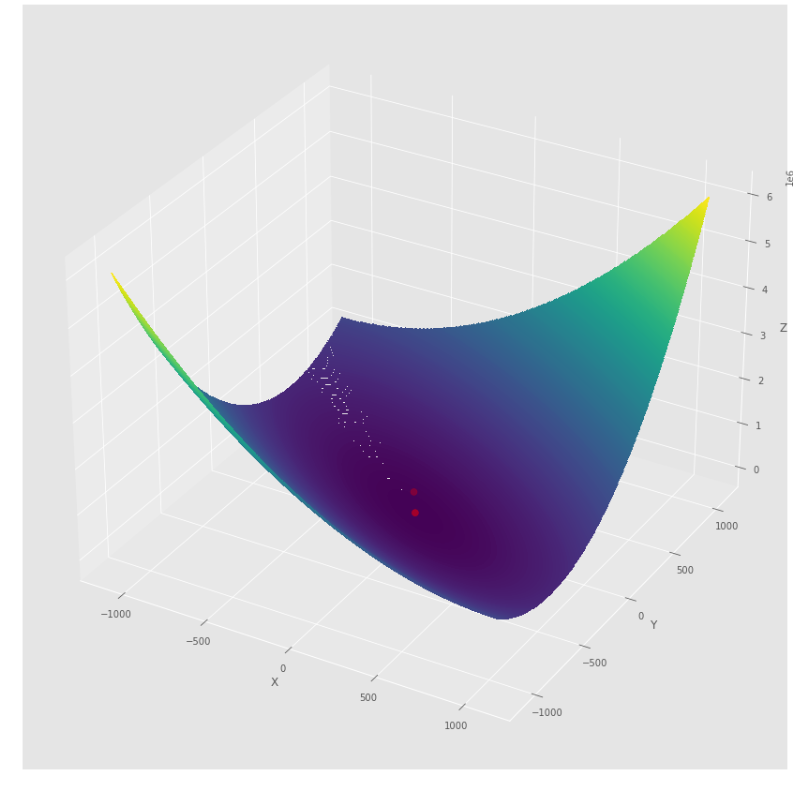
Terrain 3D
pmc . sgd ( h , X , tol , alpha )
pm3 . sgd ( h , X , tol , alpha ) Y* = [-1.01 1.52] La séquence des étapes prises par l'algorithme de descente de gradient stochastique avant d'atteindre le minimum 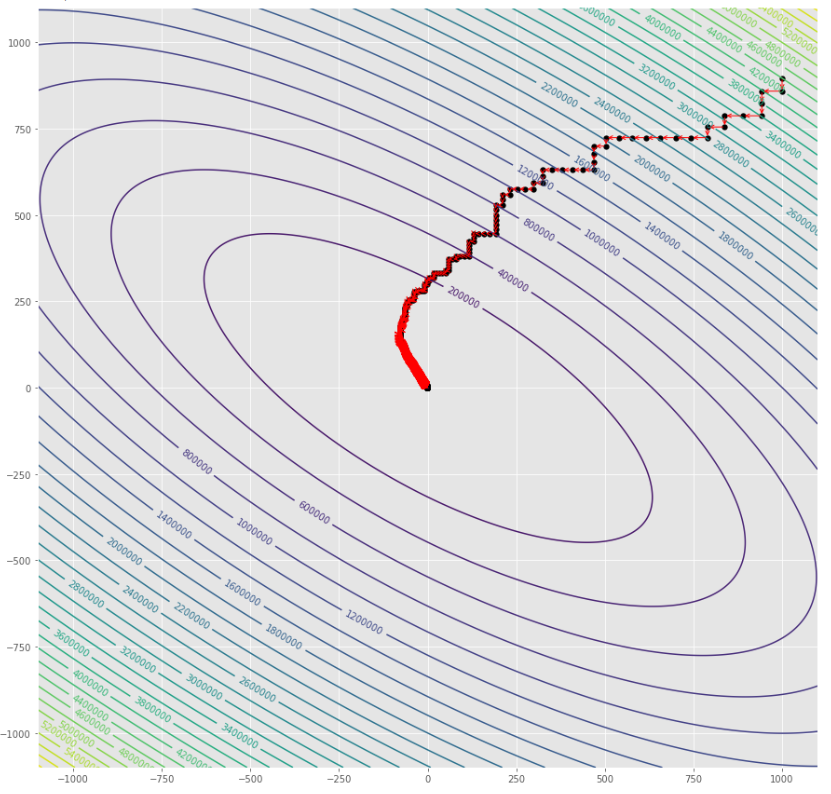
Tracé de contour 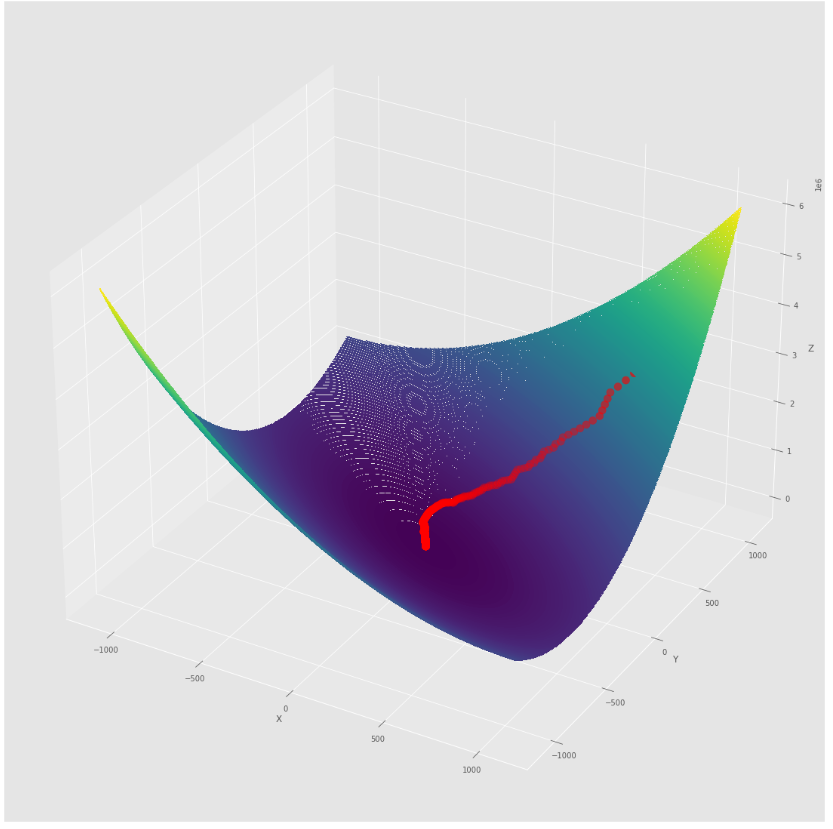
Terrain 3D
alpha = 100 #it must be high because of BLS
c = 2
pmc . sgd_with_bls ( h , X , tol , alpha , c )
pm3 . sgd_with_bls ( h , X , tol , alpha , c ) Y* = [-1. 1.5] La séquence des étapes prises par la descente de gradient stochastique avec l'algorithme BLS avant d'atteindre le minimum 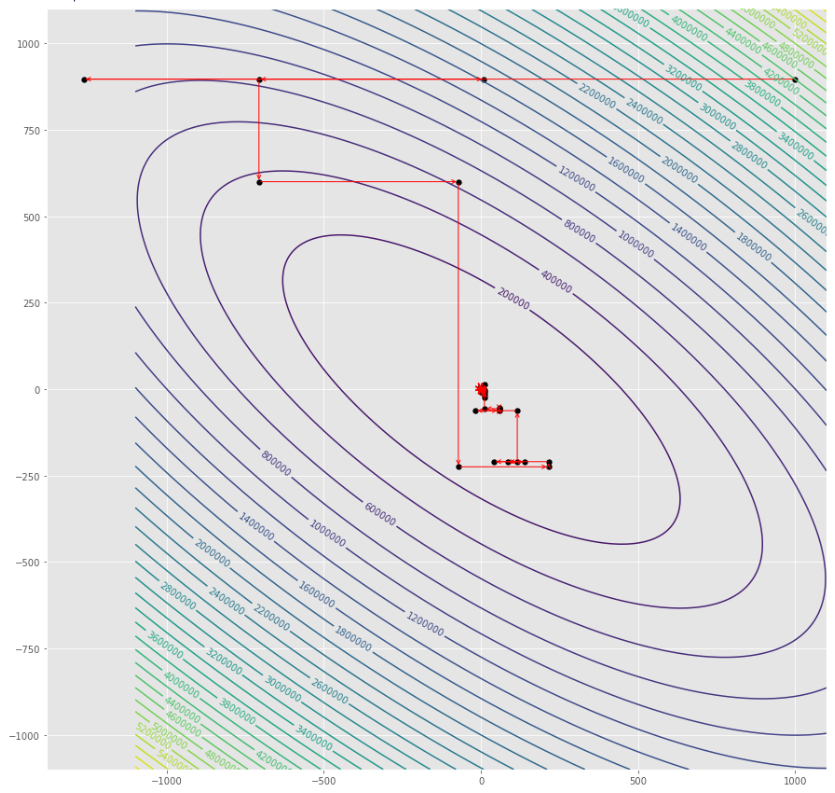
Tracé de contour 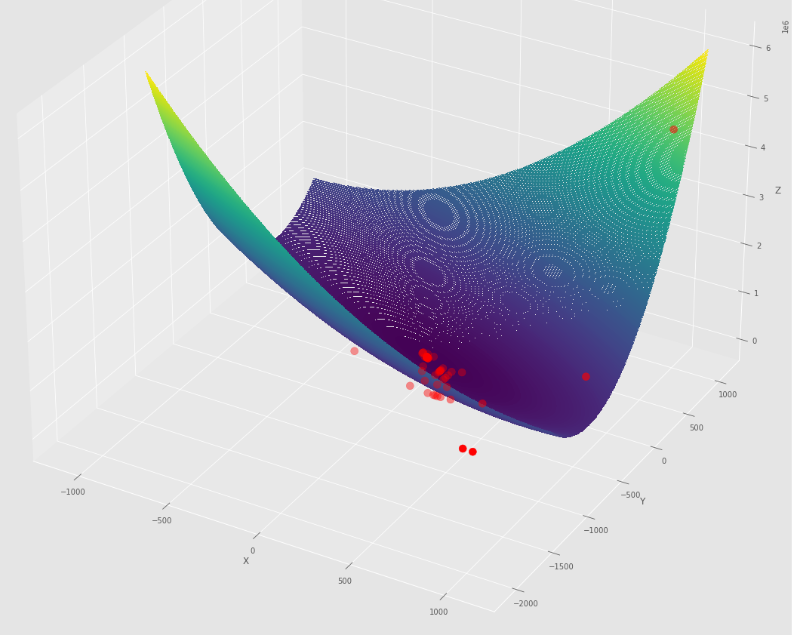
Terrain 3D
pm3 . compare_all_time ( h , X , 1.e-2 , 1.e-1 , 100 , 2 ) Temps d'exécution 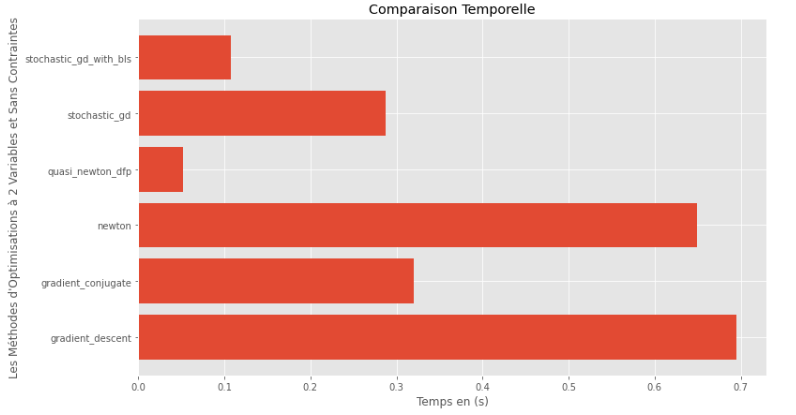
pm3 . compare_all_precision ( h , X , 1.e-2 , 1.e-1 , 100 , 2 ) Écart entre le minimum vrai et calculé 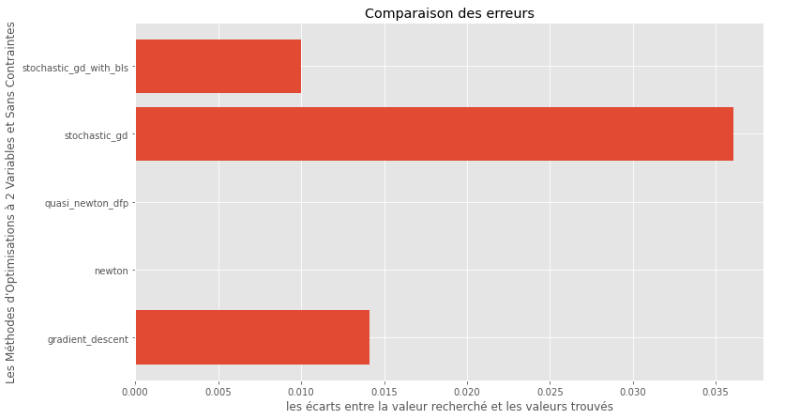
À partir des graphiques d'exécution et de précision, il peut être déduit que parmi les algorithmes évalués pour cette fonction multivariable convexe, la méthode Quasi Newton DFP apparaît comme le choix optimal, offrant un mélange de haute précision et notamment de l'exécution.
import pyoptim . my_numpy . inverse as npi 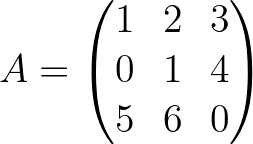
A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]]) A_1 = npi . gaussjordan ( A . copy ())
I = A @ A_1
I = np . around ( I , 1 )
print ( 'A_1 = n n ' , A_1 )
print ( ' n A_1*A = n n ' , I ) A_1 =
[[-24. 18. 5.]
[ 20. -15. -4.]
[ -5. 4. 1.]]
A_1*A =
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]] import pyoptim . my_numpy . decompose as npd A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]]) #A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ],[ - 1. , 2. , - 1. ],[ 0. , - 1. , 2. ]]) #B is positive definite
Y = np . array ([ 45 , - 78 , 95 ]) #randomly chosen column vector L , U , P = npd . LU ( A )
print ( "P = n " , P , " n n L = n " , L , " n n U = n " , U )
print ( " n " , A == P @ L @ U ) P =
[[0. 0. 1.]
[0. 1. 0.]
[1. 0. 0.]]
L =
[[1. 0. 0. ]
[0. 1. 0. ]
[0.2 0.8 1. ]]
U =
[[ 5. 6. 0. ]
[ 0. 1. 4. ]
[ 0. 0. -0.2]]
[[ True True True]
[ True True True]
[ True True True]] L = npd . choleski ( A ) # A is not positive definite
print ( L )
print ( "--------------------------------------------------" )
L = npd . choleski ( B ) # B is positive definite
print ( 'L = n ' , L , ' n ' )
C = np . around ( L @( L . T ), 1 )
print ( 'B = L@(L.T) n n ' , B == C ) A must be positive definite !
None
--------------------------------------------------
L =
[[ 1.41421356 0. 0. ]
[-0.70710678 1.22474487 0. ]
[ 0. -0.81649658 1.15470054]]
B = L@(L.T)
[[ True True True]
[ True True True]
[ True True True]] import pyoptim . my_numpy . solve as nps 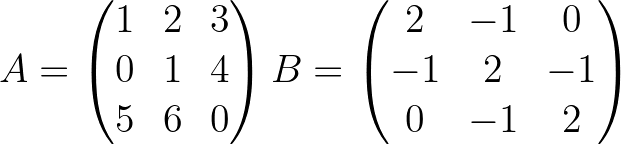
A = np . array ([[ 1. , 2. , 3. ], [ 0. , 1. , 4. ], [ 5. , 6. , 0. ]]) # A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ], [ - 1. , 2. , - 1. ], [ 0. , - 1. , 2. ]]) # B is positive definite
Y = np . array ([ 45 , - 78 , 95 ]) # randomly chosen column vector X = nps . gaussjordan ( A , Y )
print ( "X = n " , X )
print ( " n A@X=Y n " , A @ X == Y , ' n ' )
print ( '---------------------------------------------------------------' )
X = nps . gaussjordan ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n B@X=Y n " , Y_ == Y , ' n ' ) X =
[[-2009.]
[ 1690.]
[ -442.]]
A@X=Y
[[ True]
[ True]
[ True]]
---------------------------------------------------------------
X =
[[18.5]
[-8. ]
[43.5]]
B@X=Y
[[ True]
[ True]
[ True]]
X = nps . LU ( A , Y )
print ( "X* = n " , X )
print ( " n AX*=Y n " , A @ X == Y )
print ( "-------------------------------------------------------------------------------" );
X = nps . LU ( B , Y )
print ( "X* = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y ) X* =
[[-2009.]
[ 1690.]
[ -442.]]
AX*=Y
[[ True]
[ True]
[ True]]
-------------------------------------------------------------------------------
X* =
[[18.5]
[-8. ]
[43.5]]
BX*=Y
[[ True]
[ True]
[ True]] X = nps . choleski ( A , Y )
print ( "-------------------------------------------------------------------------------" )
X = nps . choleski ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y ) !! A must be positive definite !!
-------------------------------------------------------------------------------
X =
[[18.5]
[-8. ]
[43.5]]
BX*=Y
[[ True]
[ True]
[ True]]