Pyoptim:最適化とマトリックス操作のためのPythonパッケージ
Ensiasの数値分析と最適化コースのコンポーネントであるこのプロジェクトは、Mohammed v Universityが、研究室セッション中に練習したアルゴリズムをカプセル化するPythonパッケージを作成するというM. Naoum教授の提案から生まれました。約10の制約のない最適化アルゴリズムに焦点を当て、2Dおよび3Dの視覚化を提供し、計算効率と精度のパフォーマンス比較を可能にします。さらに、このプロジェクトには、反転、分解、線形システムの解決などのマトリックス操作が含まれます。これらはすべて、ラボ由来のアルゴリズムを含むパッケージ内に統合されています。
GIFソース:https://www.nsf.gov/news/mmg/mmg_disp.jsp?med_id = 78950&from = (https://aria42.com/blog/2014/12/understanding-lbfgs
このプロジェクトのすべての部分は、以下を行う方法を示すサンプルコードです。
fixed_step、accelerated_step、rexecrive_search、dichotomous_search、interval_halving、fibonacci、golden_section、armijo_backward、およびarmijo_forwardを含む、1倍の最適化アルゴリズムの実装。
勾配降下、勾配コンジュゲート、ニュートン、quasi_newton_dfp、確率的勾配降下など、さまざまな1変量最適化アルゴリズムの組み込み。
2D、輪郭、3D形式のすべてのアルゴリズムの各反復ステップの視覚化。
ランタイムと精度メトリックに焦点を当てた比較分析を実施します。
反転(ガウスヨルダンなど)、分解(Lu、Choleskiなど)、線形システムのソリューションなどのマトリックス操作の実装(Gauss-jordan、lu、choleski)。
このPythonパッケージをインストールするには:
pip install pyoptimこのデモノートブックを実行します
import pyoptim . my_scipy . onevar_optimize . minimize as soom
import pyoptim . my_plot . onevar . _2D as po2 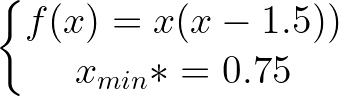
def f ( x ):
return x * ( x - 1.5 ) # analytically, argmin(f) = 0.75 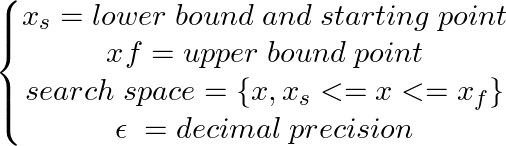
xs = - 10
xf = 10
epsilon = 1.e-2 print ( 'x* =' , soom . fixed_step ( f , xs , epsilon ))
po2 . fixed_step ( f , xs , epsilon ) x* = 0.75 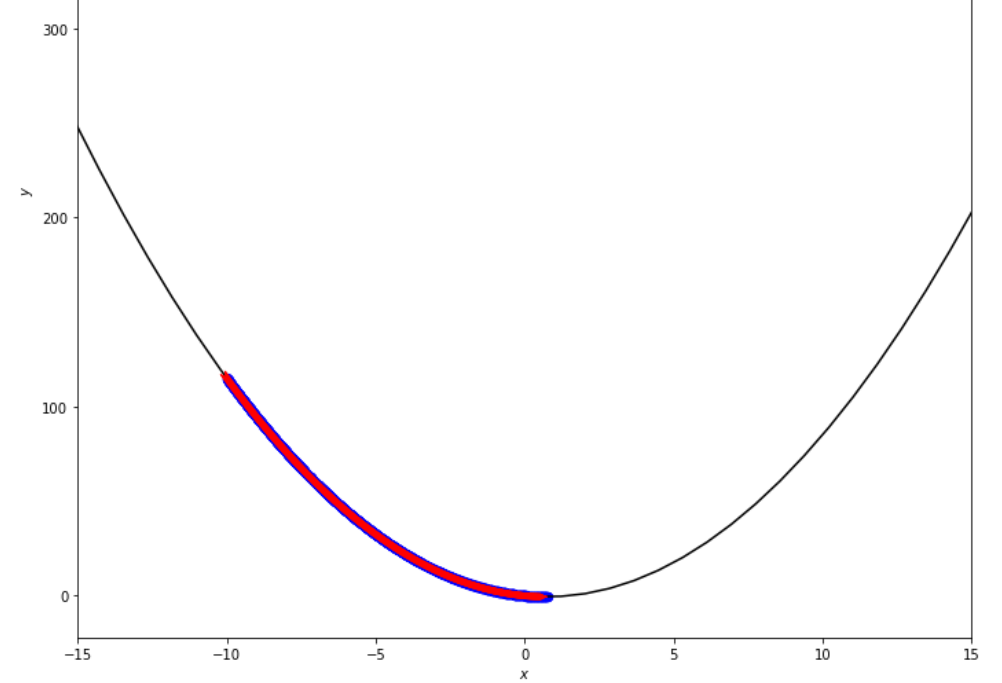
最小値に達する前に、固定ステップアルゴリズムによって取られた一連のステップ
print ( 'x* =' , soom . accelerated_step ( f , xs , epsilon ))
po2 . accelerated_step ( f , xs , epsilon ) x* = 0.86 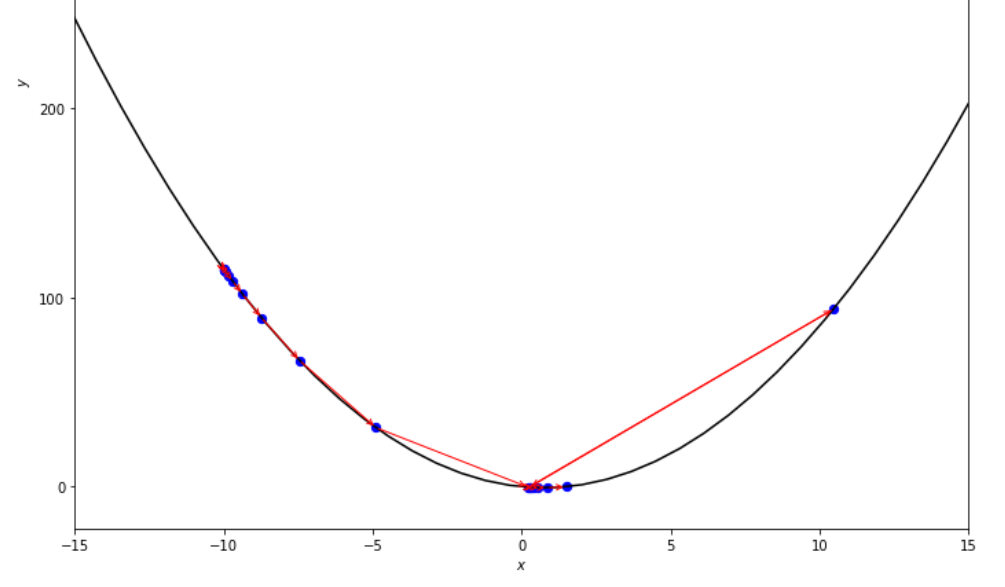
最小に到達する前に、加速ステップアルゴリズムによって取られた一連のステップ
print ( 'x* =' , soom . exhaustive_search ( f , xs , xf , epsilon ))
po2 . exhaustive_search ( f , xs , xf , epsilon ) x* = 0.75
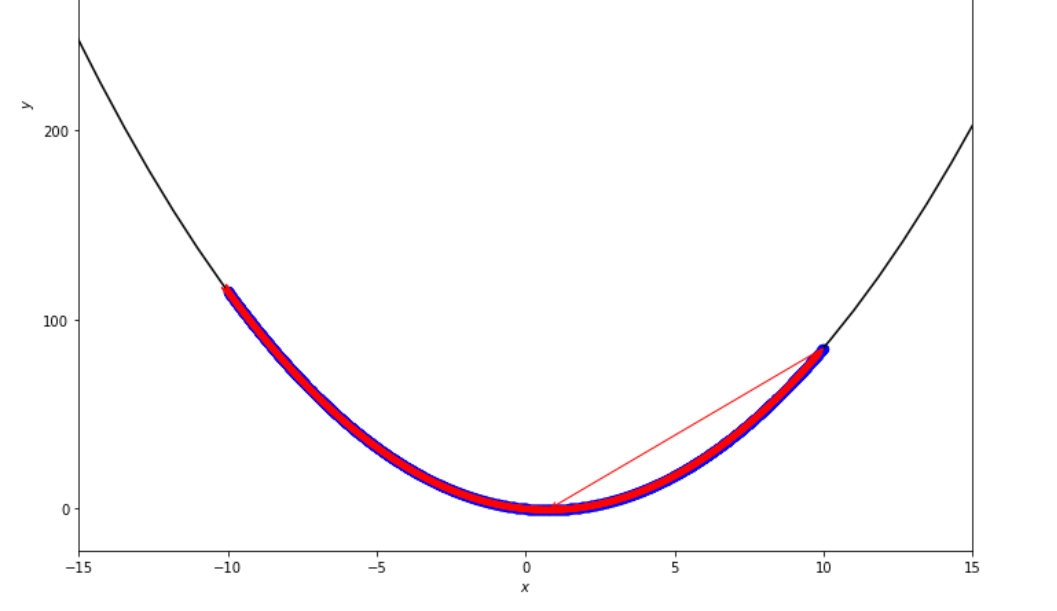
最小値に達する前に、徹底的な検索アルゴリズムによって取られた一連の手順
mini_delta = 1.e-3
print ( 'x* =' , soom . dichotomous_search ( f , xs , xf , epsilon , mini_delta ))
po2 . dichotomous_search ( f , xs , xf , epsilon , mini_delta ) x* = 0.7494742431640624
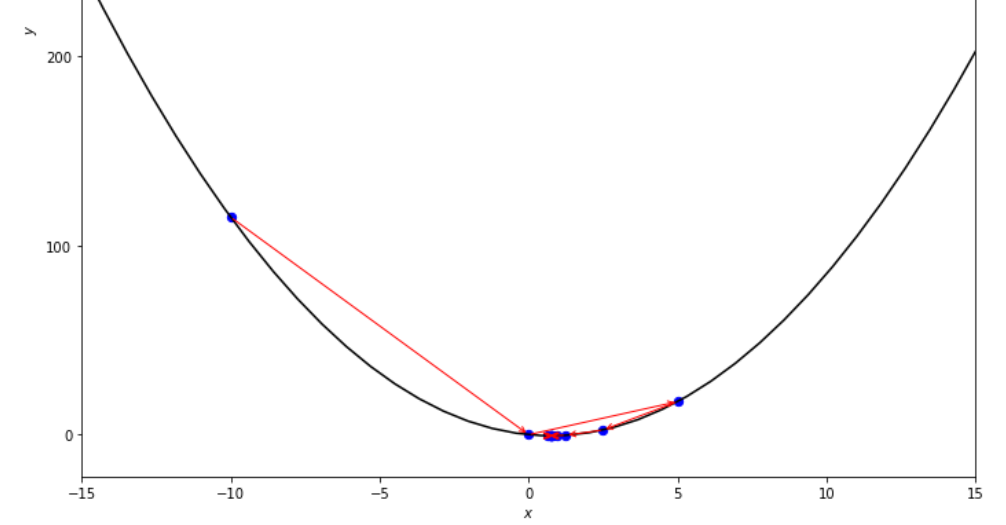
最小に到達する前に、二分法検索アルゴリズムによって取られた一連のステップ
print ( 'x* =' , soom . interval_halving ( f , xs , xf , epsilon ))
po2 . interval_halving ( f , xs , xf , epsilon ) x* = 0.75
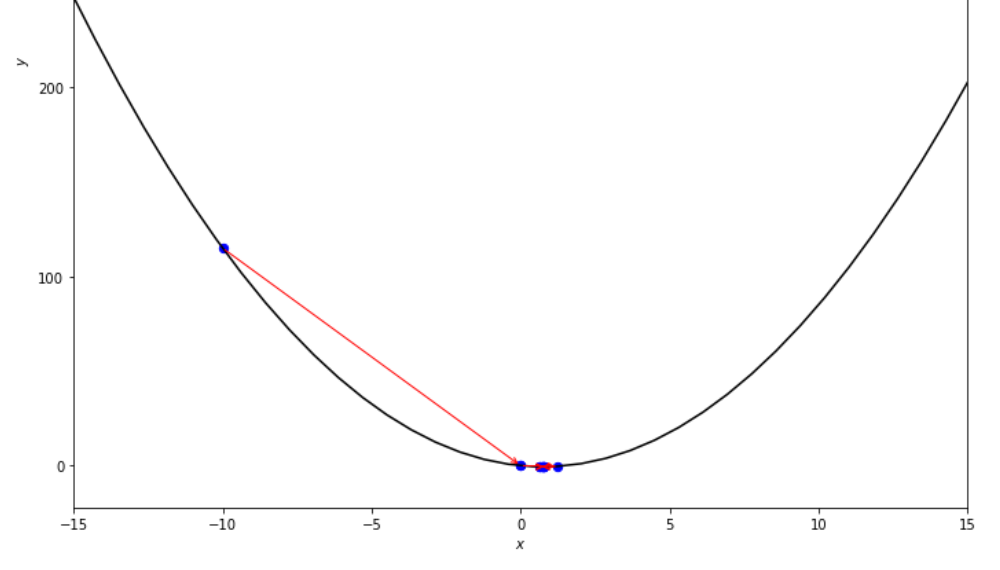
最小に到達する前に、間隔半分のアルゴリズムによって取られた一連のステップ。
n = 15
print ( 'x* =' , soom . fibonacci ( f , xs , xf , n ))
po2 . fibonacci ( f , xs , xf , n ) x* = 0.76 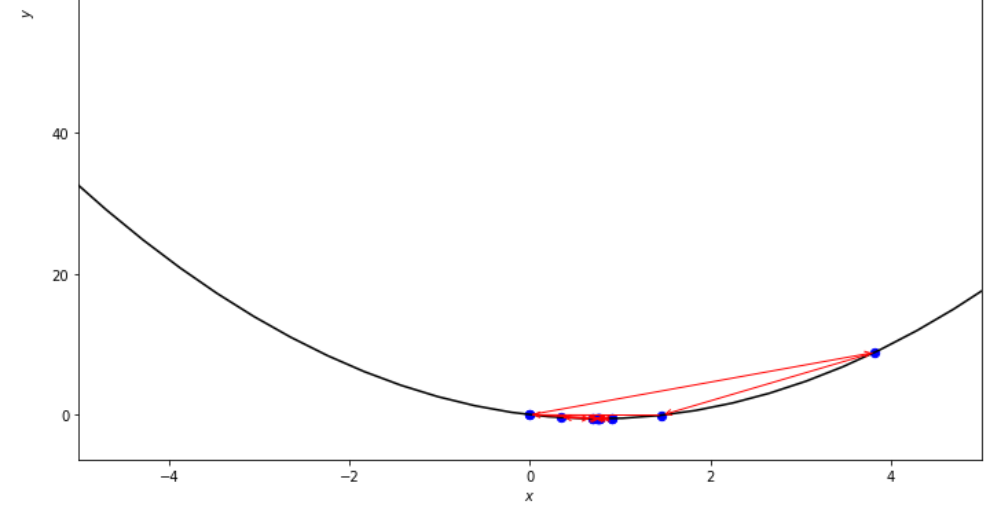
最小値に達する前に、フィボナッチアルゴリズムによって取られた一連のステップ。
print ( 'x* =' , soom . golden_section ( f , xs , xf , epsilon ))
po2 . golden_section ( f , xs , xf , epsilon ) x* = 0.75 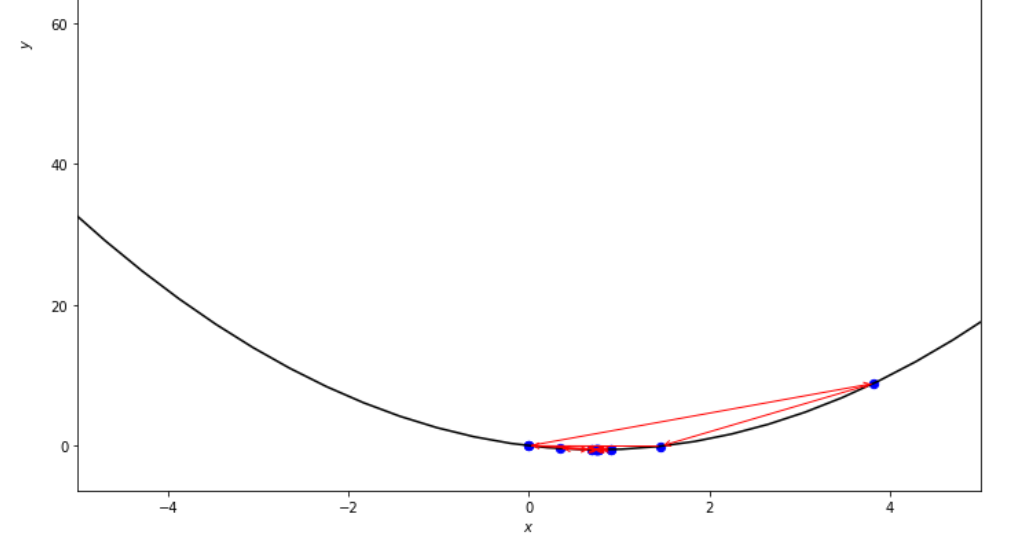
最小に到達する前にゴールデンセクションアルゴリズムによって取られた一連のステップ
ŋ = 2
xs = 100
print ( 'x* =' , soom . armijo_backward ( f , xs , ŋ , epsilon ))
po2 . armijo_backward ( f , xs , ŋ , epsilon ) x* = 0.78 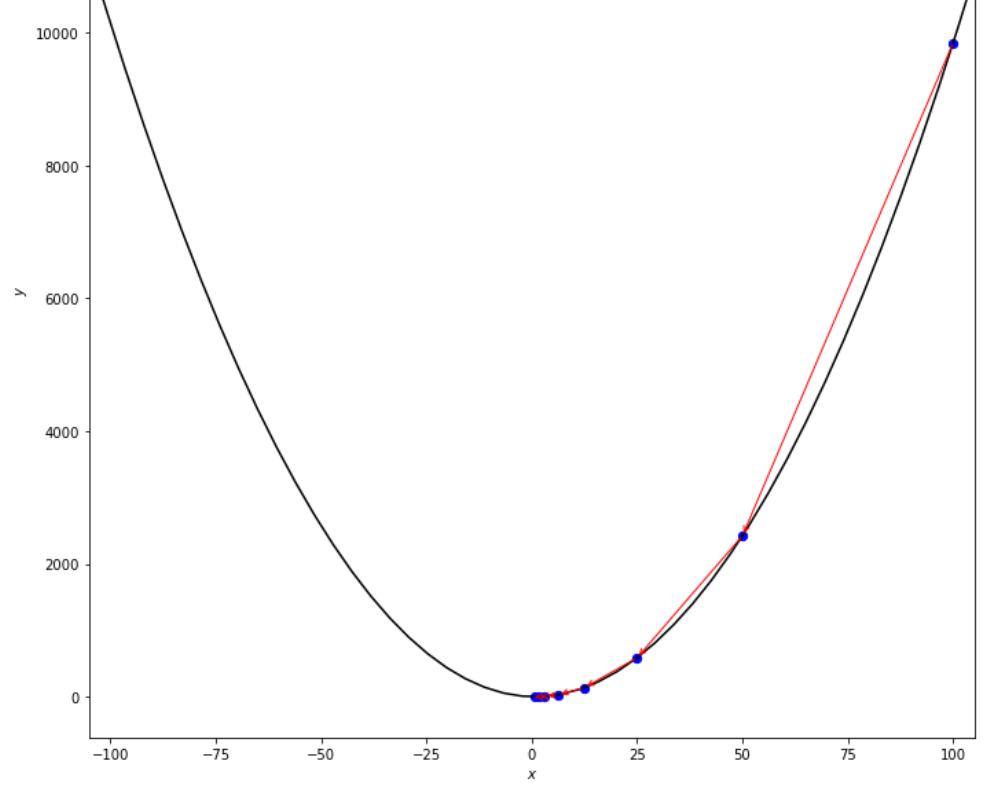
最小に到達する前に、Armijo Backwardアルゴリズムによって取られた一連のステップ
xs = 0.1
epsilon = 0.5
ŋ = 2
print ( 'x* =' , soom . armijo_forward ( f , xs , ŋ , epsilon ))
po2 . armijo_forward ( f , xs , ŋ , epsilon ) x* = 0.8 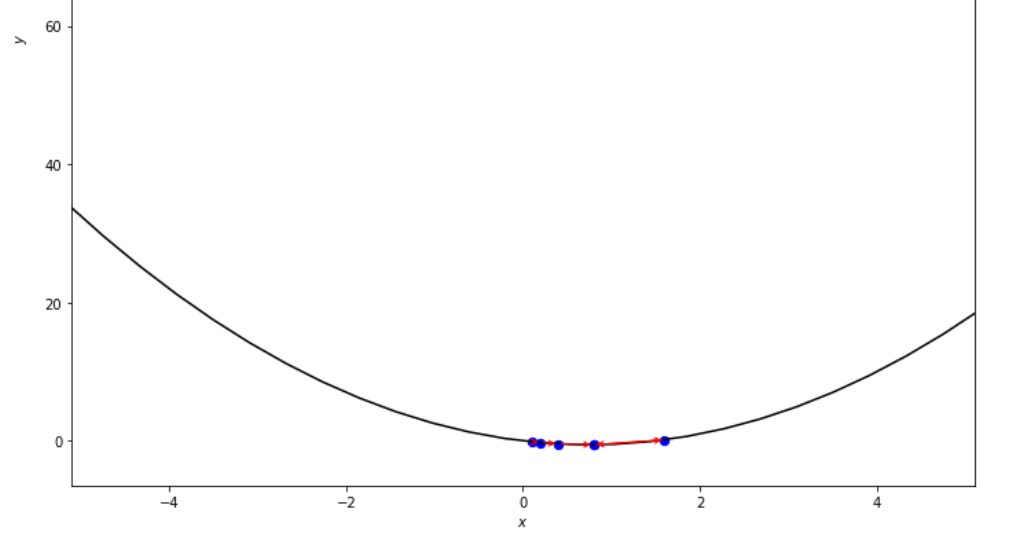
最小に到達する前に、Armijo Forwardアルゴリズムによって取られた一連のステップ
po2 . compare_all_time ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 )ランタイム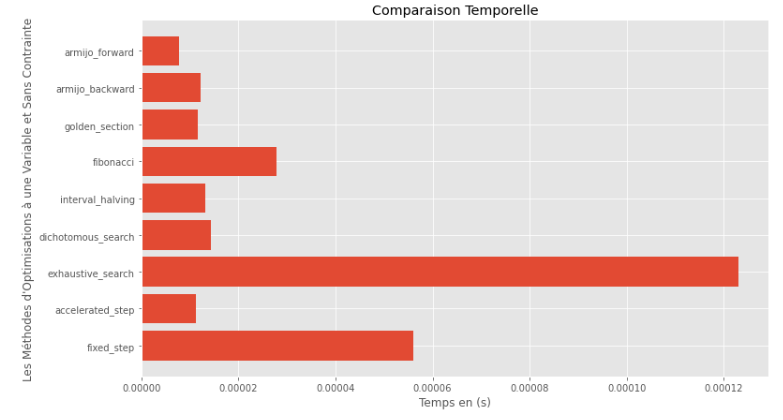
po2 . compare_all_precision ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 )真と計算された最小の間のギャップ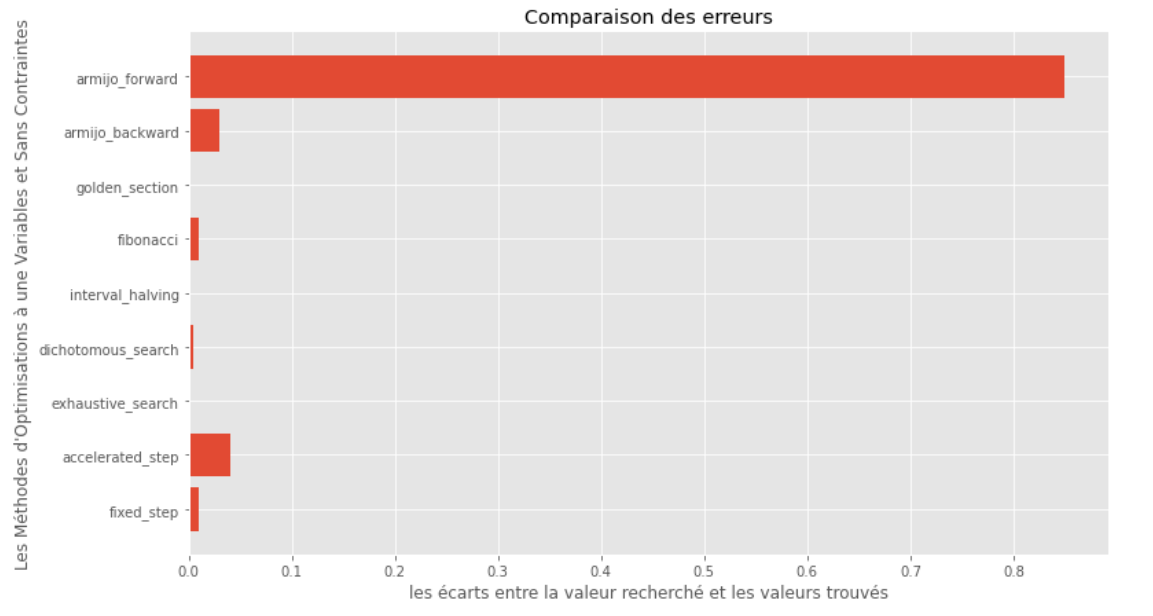
ランタイムと精度のグラフから、この凸型の単一変数関数について評価されたアルゴリズムの中で、ゴールデンセクション法が最適な選択として現れ、高精度と顕著なランタイムのブレンドを提供することを推測できます。
import pyoptim . my_plot . multivar . _3D as pm3
import pyoptim . my_plot . multivar . contour2D as pmc def h ( x ):
return x [ 0 ] - x [ 1 ] + 2 * ( x [ 0 ] ** 2 ) + 2 * x [ 1 ] * x [ 0 ] + x [ 1 ] ** 2
# analytically, argmin(f) = [-1, 1.5]アナリティ溶液
X = [ 1000 , 897 ]
alpha = 1.e-2
tol = 1.e-2 pmc . gradient_descent ( h , X , tol , alpha )
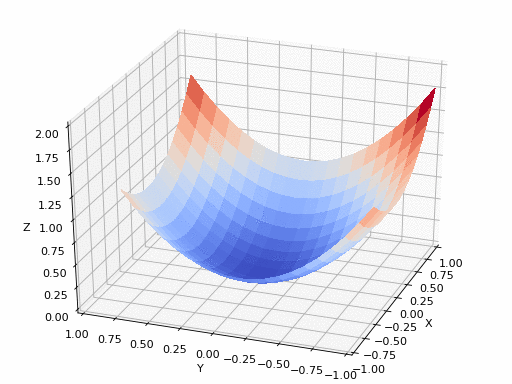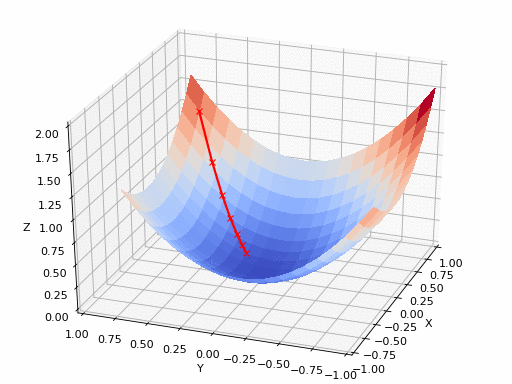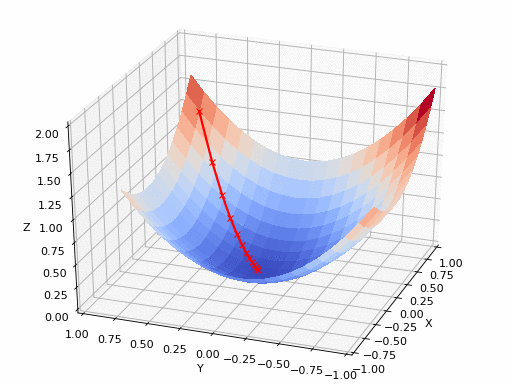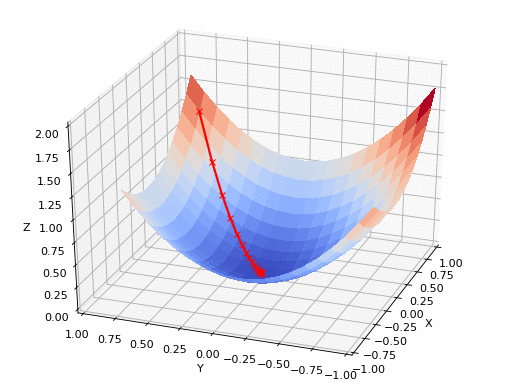
pm3 . gradient_descent ( h , X , tol , alpha ) Y* = [-1.01 1.51]勾配降下アルゴリズムが最小限に到達する前の一連のステップ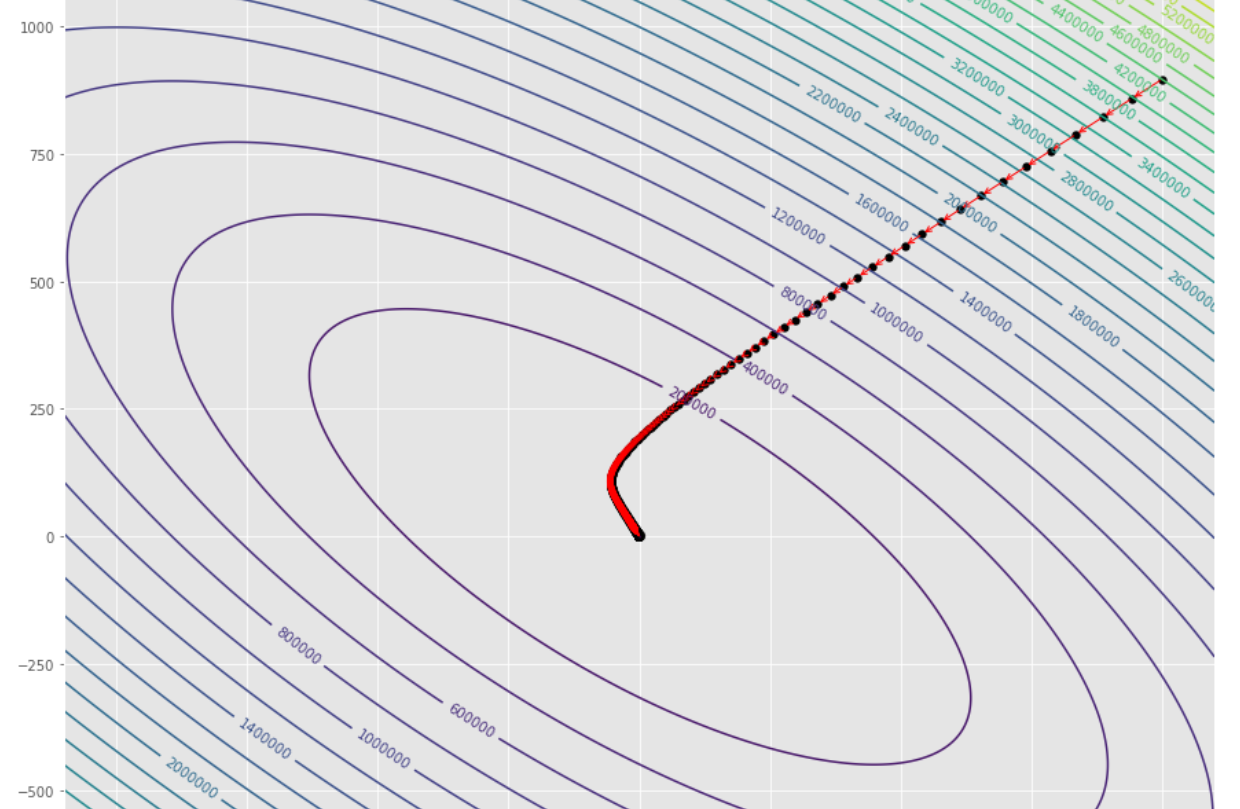
輪郭プロット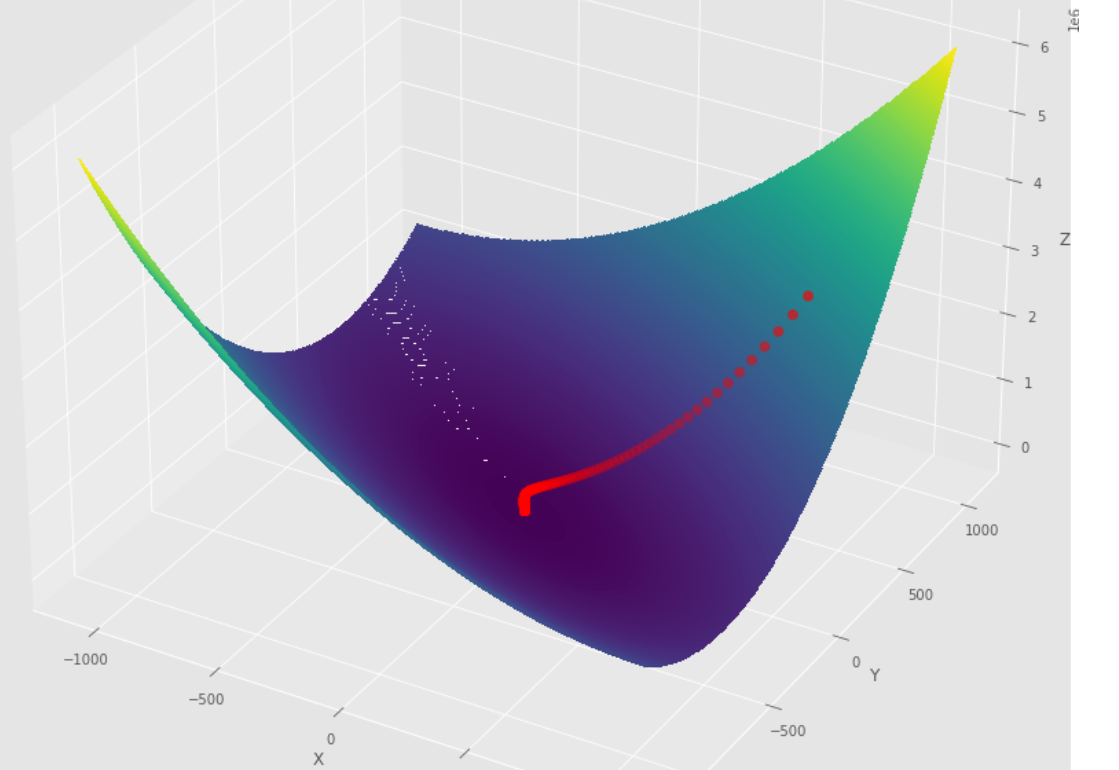
3Dプロット
pmc . gradient_conjugate ( h , X , tol )
pm3 . gradient_conjugate ( h , X , tol ) Y* = [-107.38 172.18]勾配コンジュゲートアルゴリズムによって採用された一連のステップは、最小に到達する前に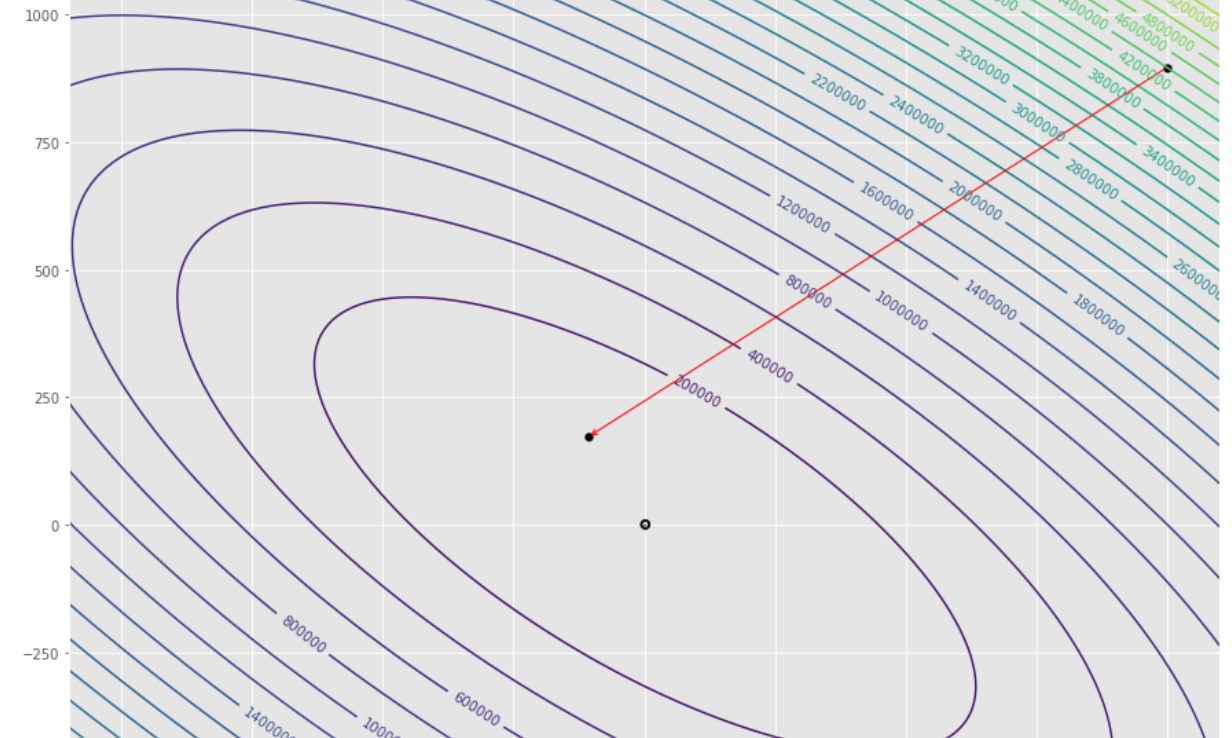
輪郭プロット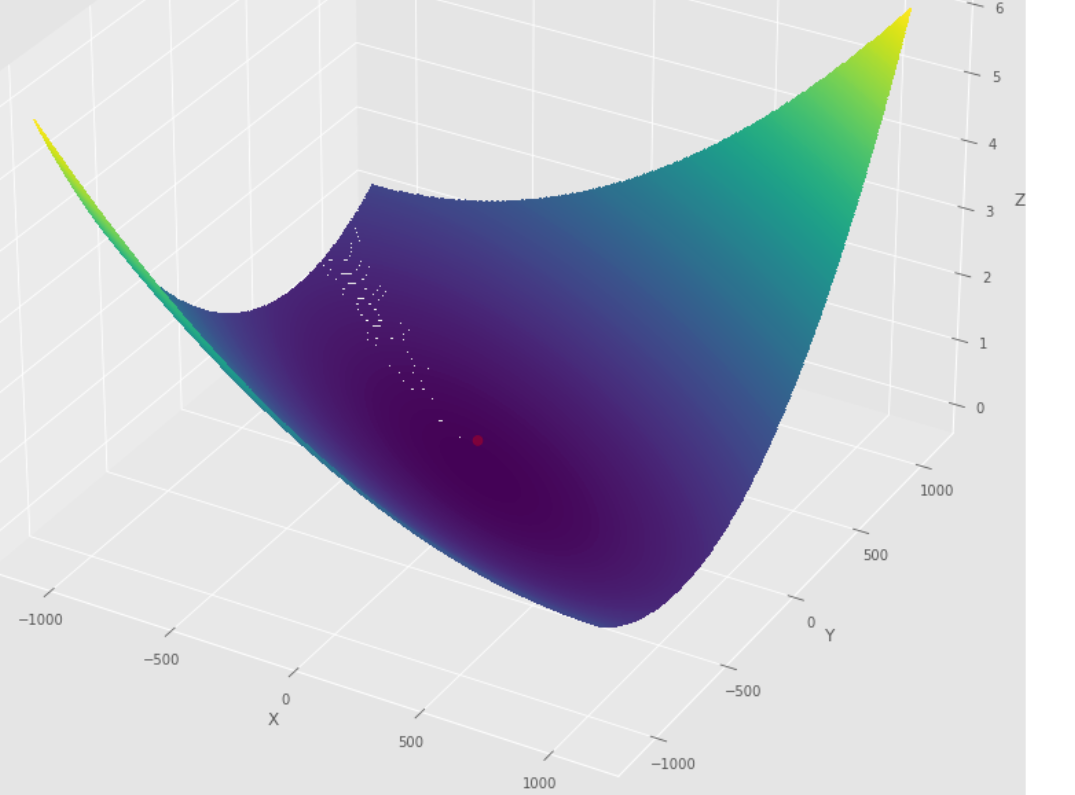
3Dプロット
pmc . newton ( h , X , tol )
pm3 . newton ( h , X , tol ) Y* = [-1. 1.5]最小値に達する前に、ニュートンアルゴリズムによって取られた一連の手順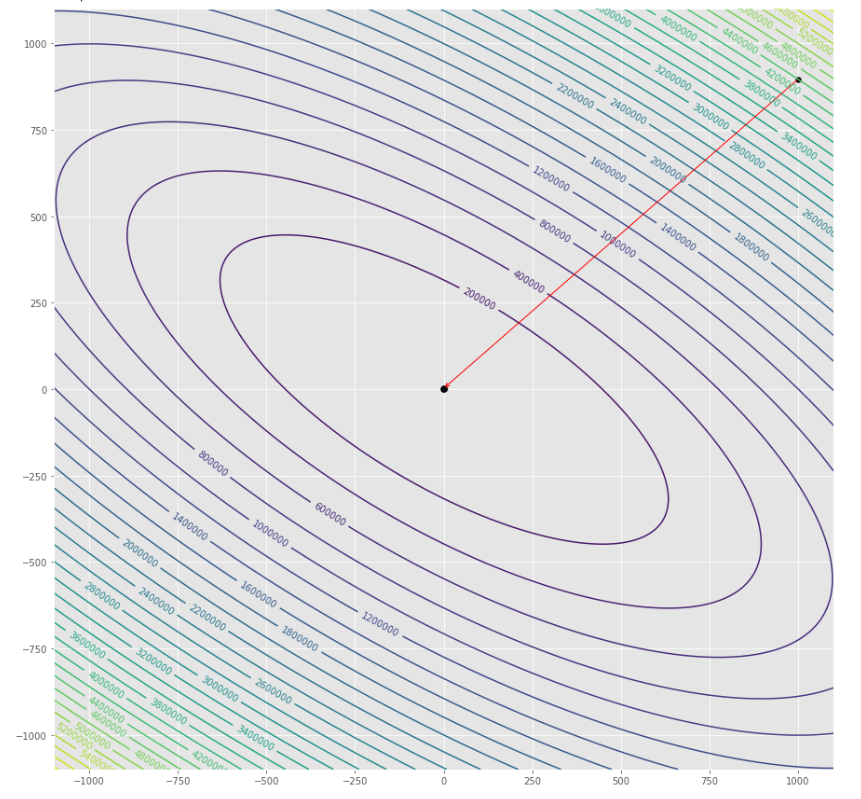
輪郭プロット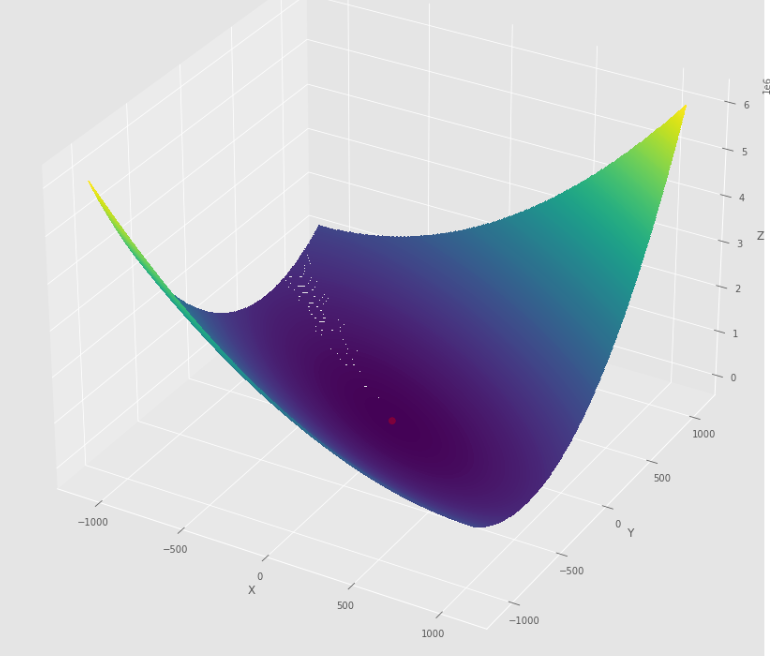
3Dプロット
pmc . quasi_newton_dfp ( h , X , tol )
pm3 . quasi_newton_dfp ( h , X , tol ) Y* = [-1. 1.5]最小に到達する前に、Quasi Newton DFPアルゴリズムによって採用された一連のステップ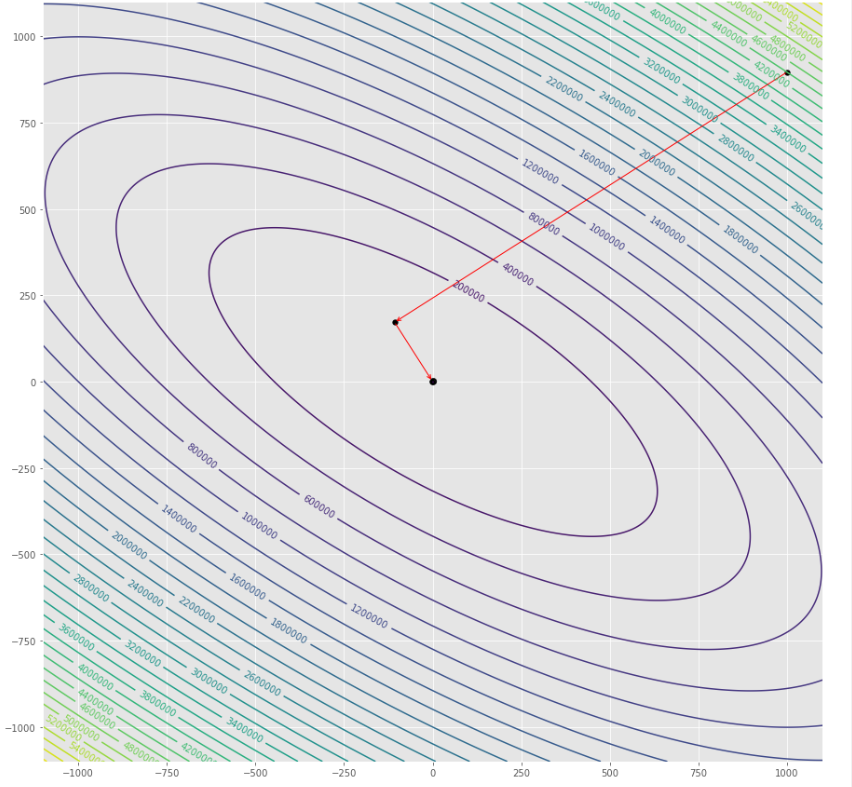
輪郭プロット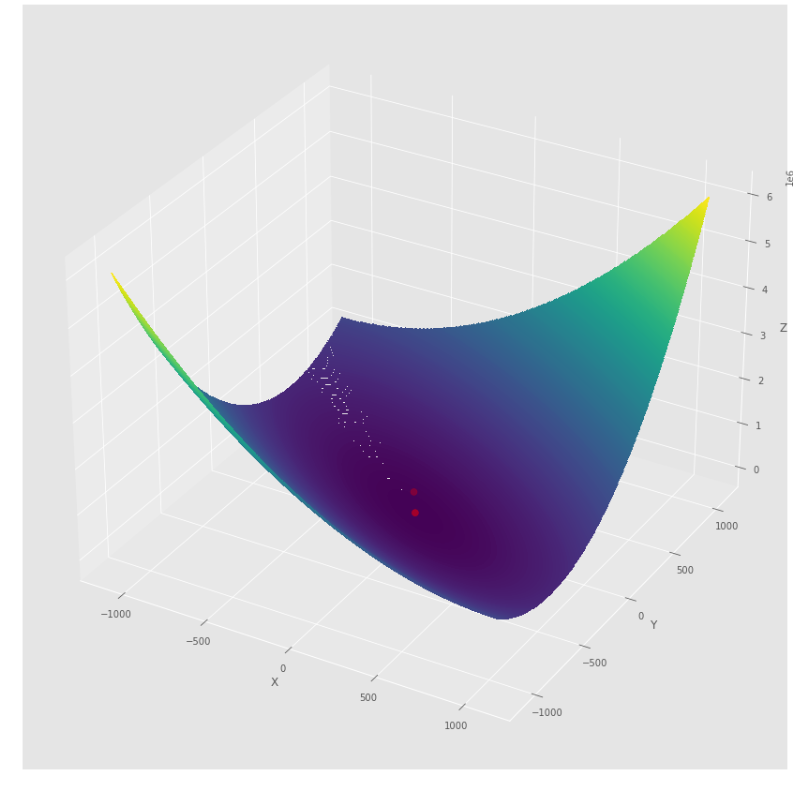
3Dプロット
pmc . sgd ( h , X , tol , alpha )
pm3 . sgd ( h , X , tol , alpha ) Y* = [-1.01 1.52]最小に到達する前に、確率勾配降下アルゴリズムによって取られた一連のステップ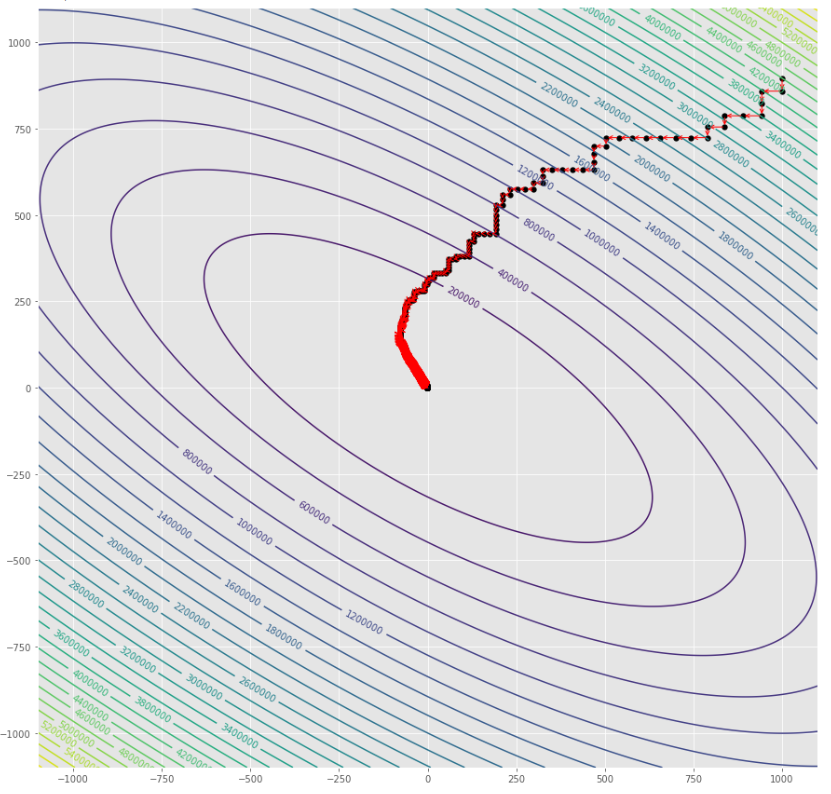
輪郭プロット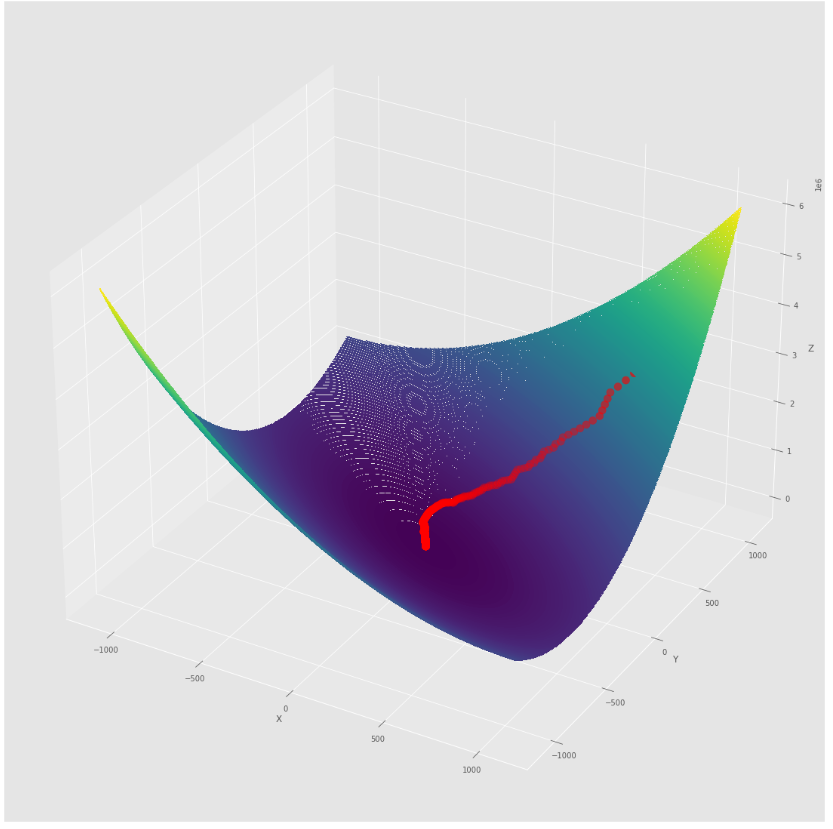
3Dプロット
alpha = 100 #it must be high because of BLS
c = 2
pmc . sgd_with_bls ( h , X , tol , alpha , c )
pm3 . sgd_with_bls ( h , X , tol , alpha , c ) Y* = [-1. 1.5]最小値に達する前に、BLSアルゴリズムを使用した確率勾配降下によって採用された一連のステップ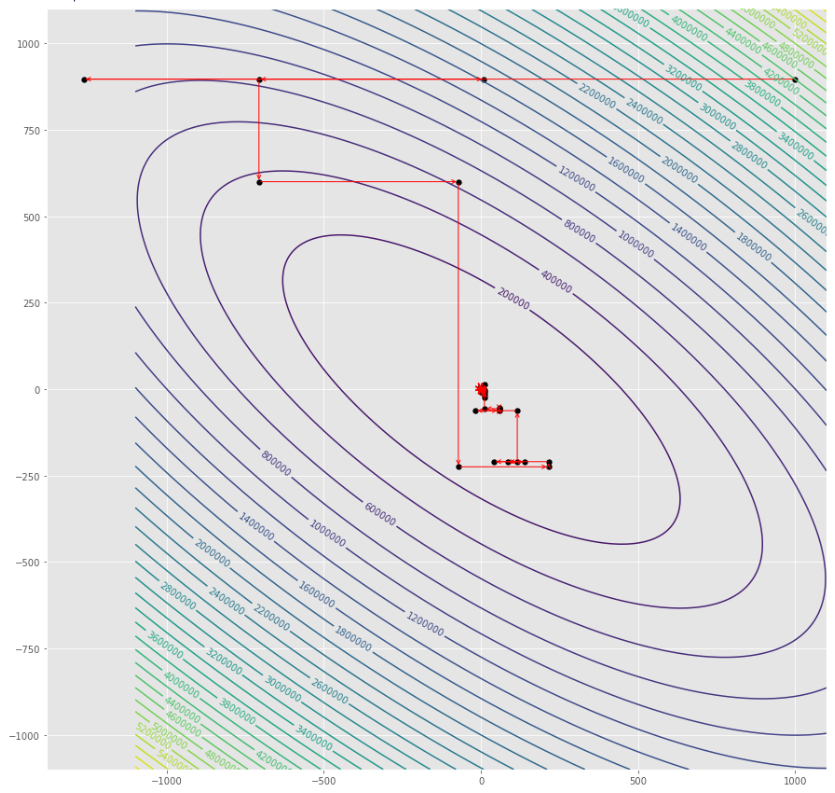
輪郭プロット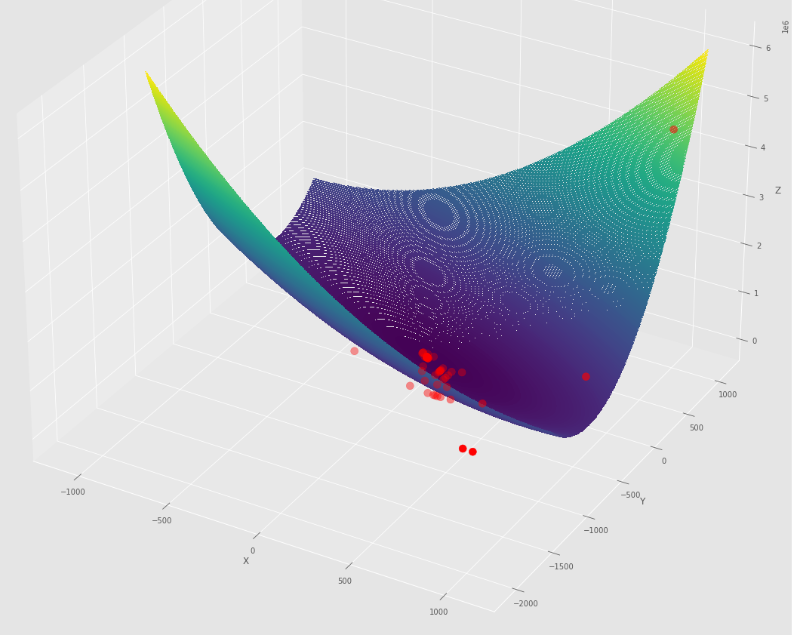
3Dプロット
pm3 . compare_all_time ( h , X , 1.e-2 , 1.e-1 , 100 , 2 )ランタイム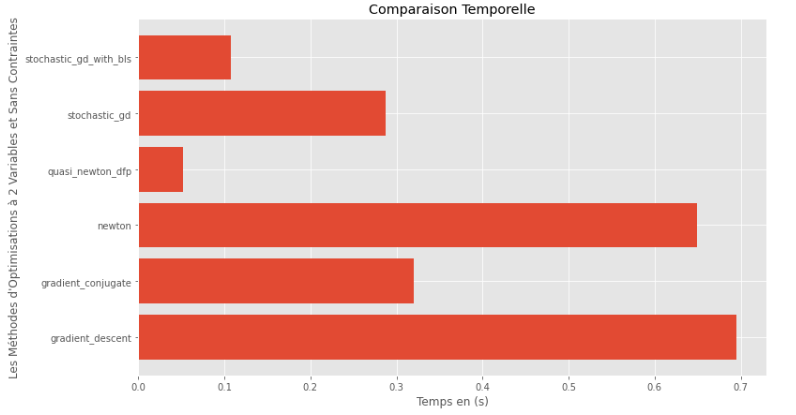
pm3 . compare_all_precision ( h , X , 1.e-2 , 1.e-1 , 100 , 2 )真と計算された最小の間のギャップ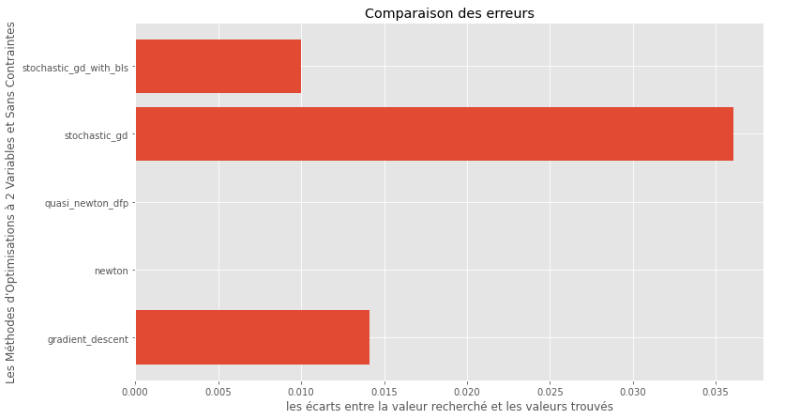
ランタイムと精度のグラフから、この凸多い多変数関数について評価されたアルゴリズムの中で、準正常な選択肢として準精度と顕著なランタイムのブレンドを提供することが最適な選択として現れると推測できます。
import pyoptim . my_numpy . inverse as npi 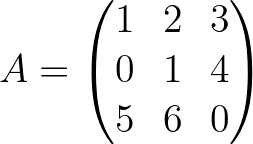
A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]]) A_1 = npi . gaussjordan ( A . copy ())
I = A @ A_1
I = np . around ( I , 1 )
print ( 'A_1 = n n ' , A_1 )
print ( ' n A_1*A = n n ' , I ) A_1 =
[[-24. 18. 5.]
[ 20. -15. -4.]
[ -5. 4. 1.]]
A_1*A =
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]] import pyoptim . my_numpy . decompose as npd A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]]) #A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ],[ - 1. , 2. , - 1. ],[ 0. , - 1. , 2. ]]) #B is positive definite
Y = np . array ([ 45 , - 78 , 95 ]) #randomly chosen column vector L , U , P = npd . LU ( A )
print ( "P = n " , P , " n n L = n " , L , " n n U = n " , U )
print ( " n " , A == P @ L @ U ) P =
[[0. 0. 1.]
[0. 1. 0.]
[1. 0. 0.]]
L =
[[1. 0. 0. ]
[0. 1. 0. ]
[0.2 0.8 1. ]]
U =
[[ 5. 6. 0. ]
[ 0. 1. 4. ]
[ 0. 0. -0.2]]
[[ True True True]
[ True True True]
[ True True True]] L = npd . choleski ( A ) # A is not positive definite
print ( L )
print ( "--------------------------------------------------" )
L = npd . choleski ( B ) # B is positive definite
print ( 'L = n ' , L , ' n ' )
C = np . around ( L @( L . T ), 1 )
print ( 'B = L@(L.T) n n ' , B == C ) A must be positive definite !
None
--------------------------------------------------
L =
[[ 1.41421356 0. 0. ]
[-0.70710678 1.22474487 0. ]
[ 0. -0.81649658 1.15470054]]
B = L@(L.T)
[[ True True True]
[ True True True]
[ True True True]] import pyoptim . my_numpy . solve as nps 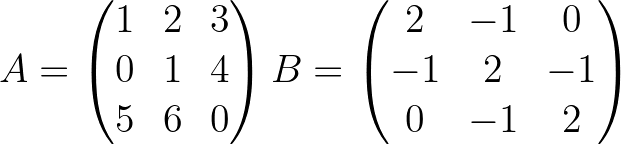
A = np . array ([[ 1. , 2. , 3. ], [ 0. , 1. , 4. ], [ 5. , 6. , 0. ]]) # A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ], [ - 1. , 2. , - 1. ], [ 0. , - 1. , 2. ]]) # B is positive definite
Y = np . array ([ 45 , - 78 , 95 ]) # randomly chosen column vector X = nps . gaussjordan ( A , Y )
print ( "X = n " , X )
print ( " n A@X=Y n " , A @ X == Y , ' n ' )
print ( '---------------------------------------------------------------' )
X = nps . gaussjordan ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n B@X=Y n " , Y_ == Y , ' n ' ) X =
[[-2009.]
[ 1690.]
[ -442.]]
A@X=Y
[[ True]
[ True]
[ True]]
---------------------------------------------------------------
X =
[[18.5]
[-8. ]
[43.5]]
B@X=Y
[[ True]
[ True]
[ True]]
X = nps . LU ( A , Y )
print ( "X* = n " , X )
print ( " n AX*=Y n " , A @ X == Y )
print ( "-------------------------------------------------------------------------------" );
X = nps . LU ( B , Y )
print ( "X* = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y ) X* =
[[-2009.]
[ 1690.]
[ -442.]]
AX*=Y
[[ True]
[ True]
[ True]]
-------------------------------------------------------------------------------
X* =
[[18.5]
[-8. ]
[43.5]]
BX*=Y
[[ True]
[ True]
[ True]] X = nps . choleski ( A , Y )
print ( "-------------------------------------------------------------------------------" )
X = nps . choleski ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y ) !! A must be positive definite !!
-------------------------------------------------------------------------------
X =
[[18.5]
[-8. ]
[43.5]]
BX*=Y
[[ True]
[ True]
[ True]]