Pyoptim: Python -Paket für Optimierung und Matrixoperationen
Dieses Projekt, ein Bestandteil des numerischen Analyse- und Optimierungskurses in den Folgen, Mohammed V University, entstand aus dem Vorschlag von Professor M. Naum, ein Python -Paket zu erstellen, das Algorithmen verkapsend während der Laborsitzungen praktiziert. Es konzentriert sich auf etwa zehn uneingeschränkte Optimierungsalgorithmen, die 2D- und 3D -Visualisierungen anbieten und einen Leistungsvergleich der Recheneffizienz und Genauigkeit ermöglichen. Darüber hinaus umfasst das Projekt Matrixoperationen wie Inversion, Zersetzung und Lösung linearer Systeme, die alle in das Paket integriert sind, das die von Labor abgeleiteten Algorithmen enthält.
GIF-Quelle: https://www.nsf.gov/news/mmg/mmg_disp.jsp?med_id=78950&from= weibliches(https://aria42.com/blog/2014/12/undernanding-lbfgs
Jeder Teil dieses Projekts ist ein Beispielcode, der zeigt, wie man Folgendes macht:
Implementierung von One-Variable-Optimierungsalgorithmen, umfassende Fixed_Step, Accelerated_step, erschleppende_search, Dichotomous_Search, Interval_Halving, Fibonacci, Golden_section, Armijo_Backward und Armijo_forward.
Einbeziehung verschiedener Ein-variabler-Optimierungsalgorithmen, einschließlich Gradientenabstieg, Gradientenkonjugat, Newton, quasi_newton_dfp, stochastischer Gradientenabstieg.
Visualisierung jedes Iterationsschritts für alle Algorithmen in 2D-, Kontur- und 3D -Formaten.
Durchführung einer vergleichenden Analyse mit Schwerpunkt auf ihren Laufzeit- und Genauigkeitsmetriken.
Implementierung von Matrixoperationen wie Inversion (z. B. Gauß-Jordanien), Zersetzung (z. B. Lu, Choleski) und Lösungen für lineare Systeme (z. B. Gauß-Jordan, Lu, Choleski).
So installieren Sie dieses Python -Paket:
pip install pyoptimFühren Sie dieses Demo -Notizbuch aus
import pyoptim . my_scipy . onevar_optimize . minimize as soom
import pyoptim . my_plot . onevar . _2D as po2 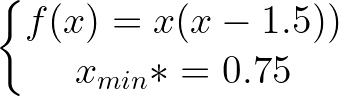
def f ( x ):
return x * ( x - 1.5 ) # analytically, argmin(f) = 0.75 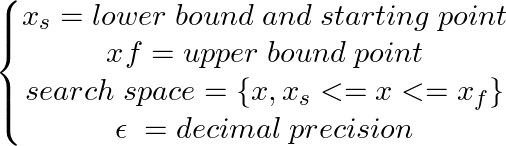
xs = - 10
xf = 10
epsilon = 1.e-2 print ( 'x* =' , soom . fixed_step ( f , xs , epsilon ))
po2 . fixed_step ( f , xs , epsilon ) x* = 0.75 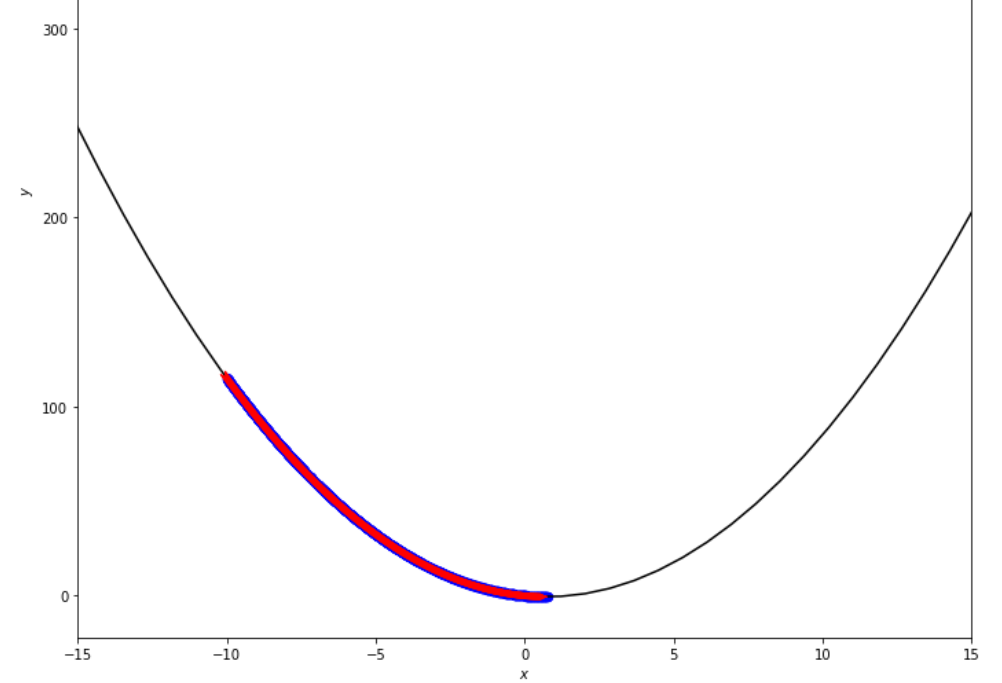
Die Abfolge der Schritte, die der feste Schrittalgorithmus unternommen hat
print ( 'x* =' , soom . accelerated_step ( f , xs , epsilon ))
po2 . accelerated_step ( f , xs , epsilon ) x* = 0.86 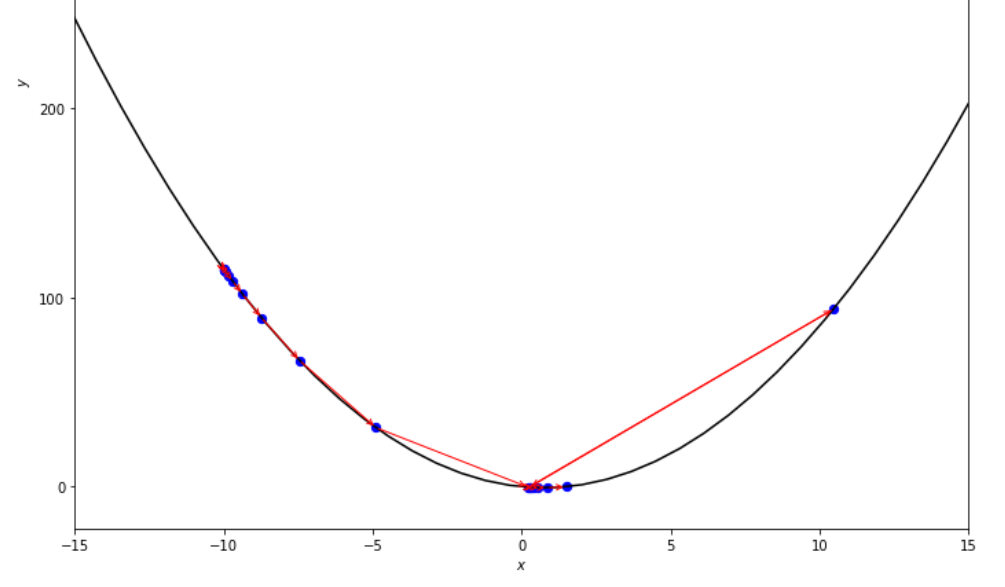
Die Abfolge der Schritte, die der beschleunigte Stufenalgorithmus unternommen hat
print ( 'x* =' , soom . exhaustive_search ( f , xs , xf , epsilon ))
po2 . exhaustive_search ( f , xs , xf , epsilon ) x* = 0.75
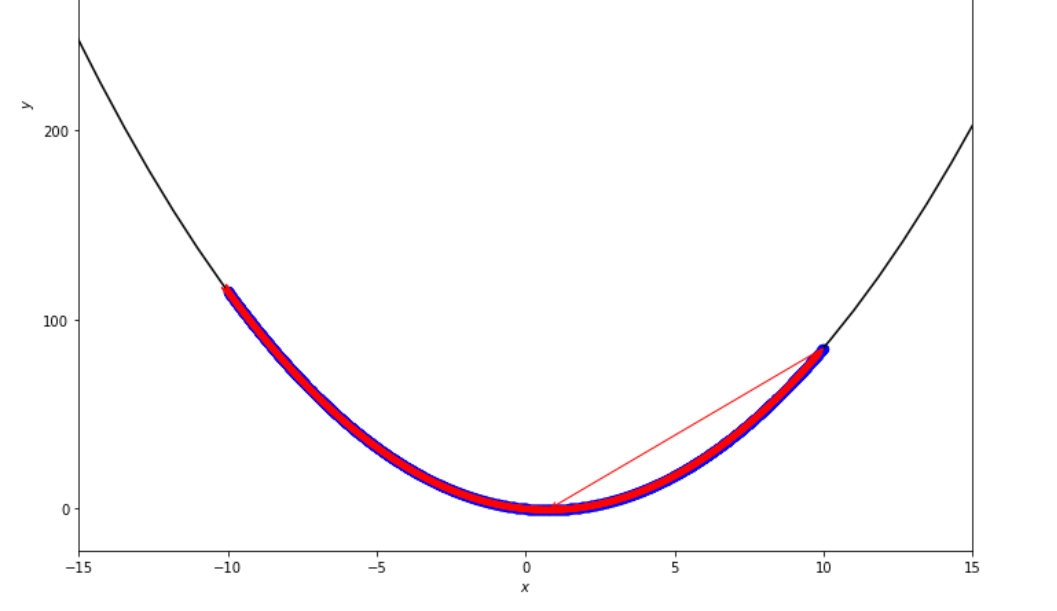
Die Abfolge der Schritte, die der erschöpfende Suchalgorithmus unternommen hat, bevor Sie das Minimum erreichen
mini_delta = 1.e-3
print ( 'x* =' , soom . dichotomous_search ( f , xs , xf , epsilon , mini_delta ))
po2 . dichotomous_search ( f , xs , xf , epsilon , mini_delta ) x* = 0.7494742431640624
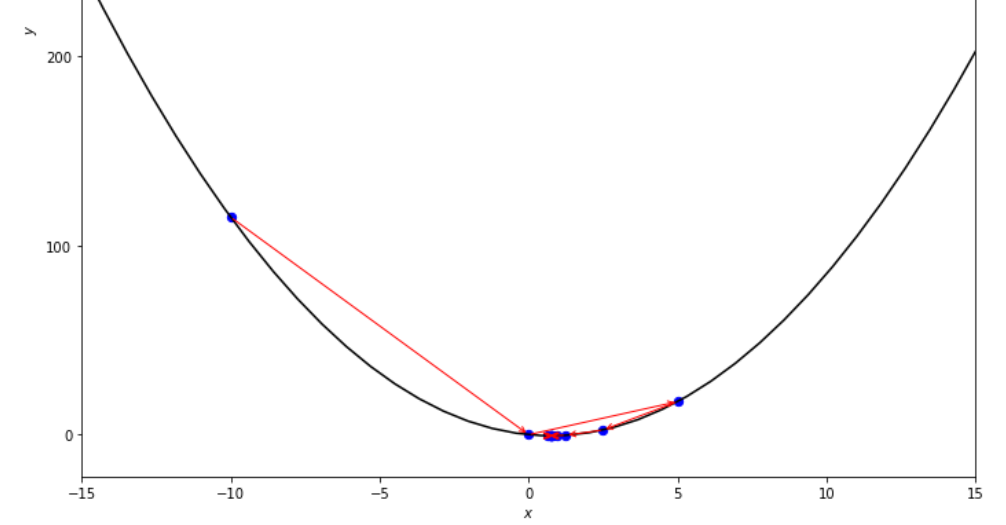
Die Abfolge der Schritte, die der dichotome Suchalgorithmus unternommen hat, bevor er das Minimum erreicht
print ( 'x* =' , soom . interval_halving ( f , xs , xf , epsilon ))
po2 . interval_halving ( f , xs , xf , epsilon ) x* = 0.75
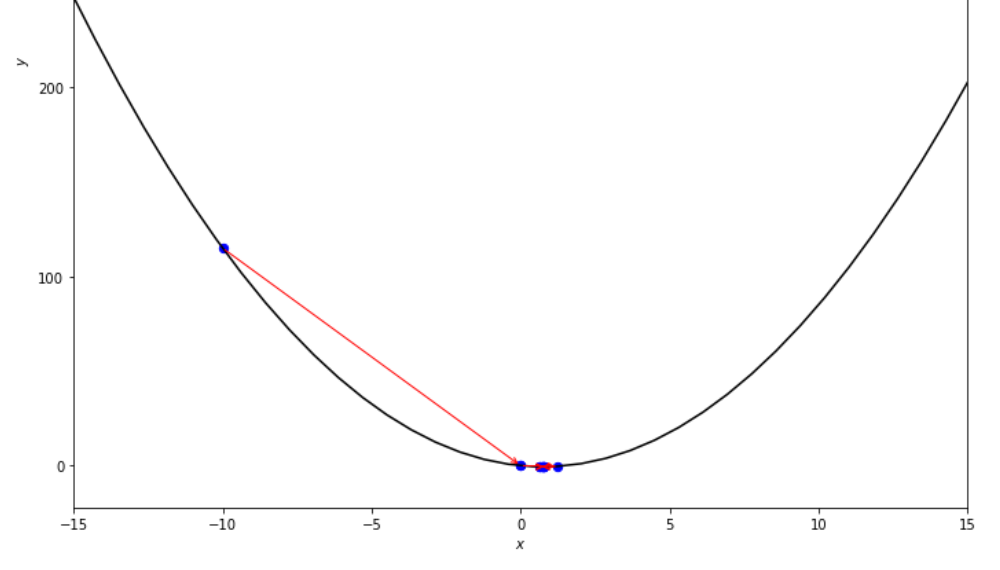
Die Abfolge der Schritte, die durch den Intervall -Halb -Algorithmus unternommen wurden, bevor er das Minimum erreicht hat.
n = 15
print ( 'x* =' , soom . fibonacci ( f , xs , xf , n ))
po2 . fibonacci ( f , xs , xf , n ) x* = 0.76 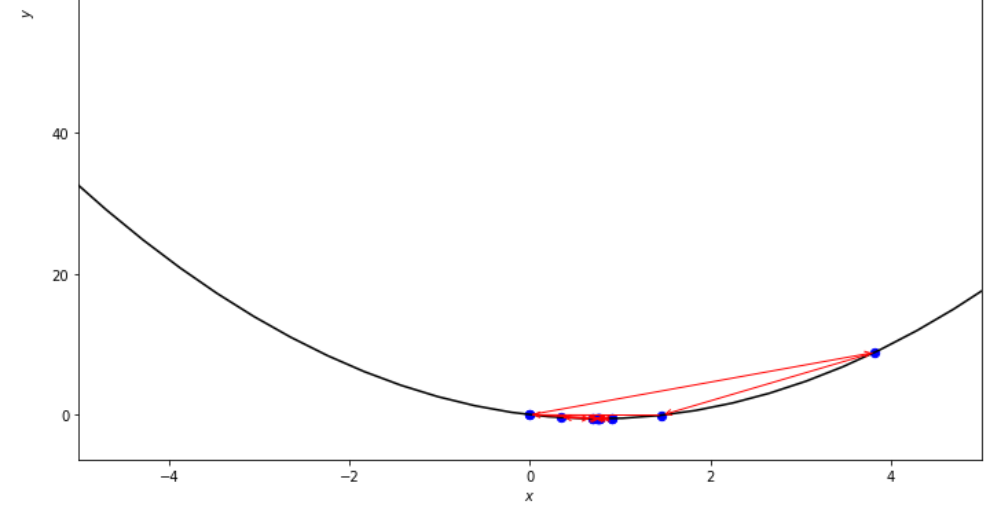
Die Abfolge der Schritte, die der Fibonacci -Algorithmus unternommen hat, bevor er das Minimum erreicht hat.
print ( 'x* =' , soom . golden_section ( f , xs , xf , epsilon ))
po2 . golden_section ( f , xs , xf , epsilon ) x* = 0.75 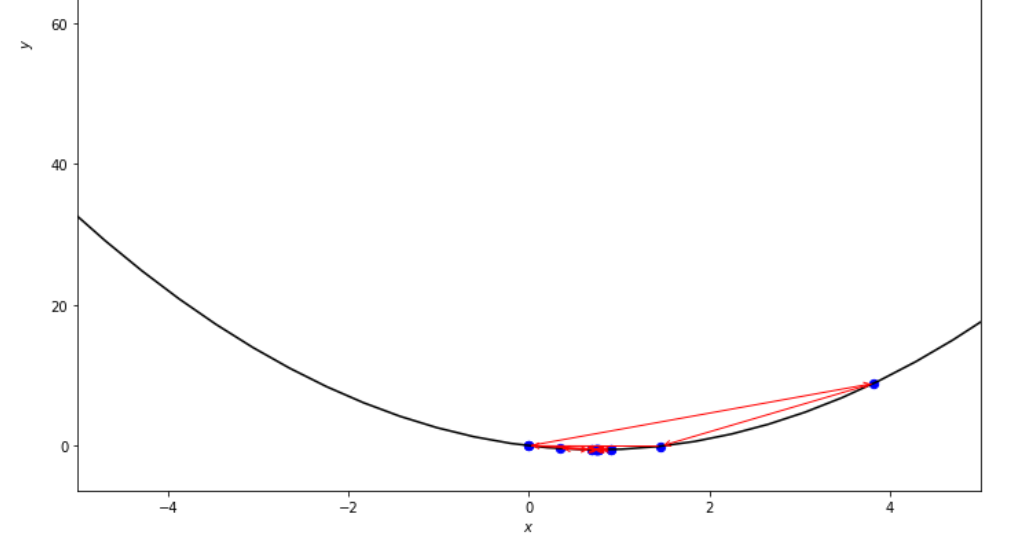
Die Abfolge der Schritte, die der Algorithmus des goldenen Abschnitts unternommen hat
ŋ = 2
xs = 100
print ( 'x* =' , soom . armijo_backward ( f , xs , ŋ , epsilon ))
po2 . armijo_backward ( f , xs , ŋ , epsilon ) x* = 0.78 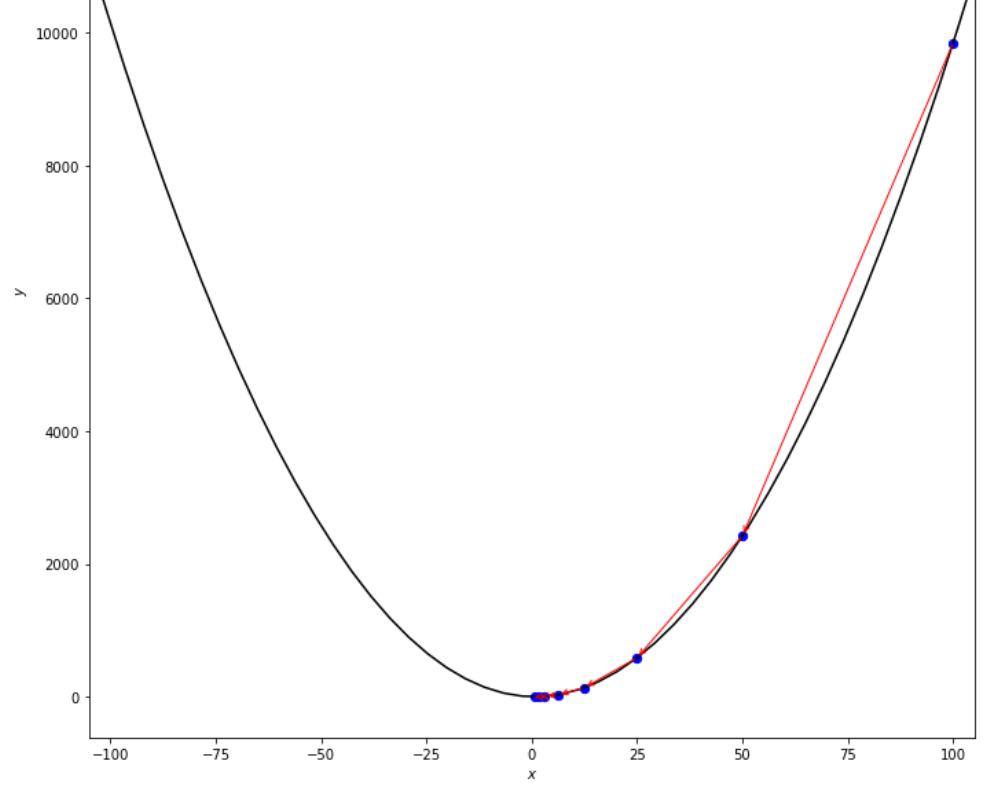
Die Abfolge der Schritte, die der Armijo rückwärts -Algorithmus unternommen hat
xs = 0.1
epsilon = 0.5
ŋ = 2
print ( 'x* =' , soom . armijo_forward ( f , xs , ŋ , epsilon ))
po2 . armijo_forward ( f , xs , ŋ , epsilon ) x* = 0.8 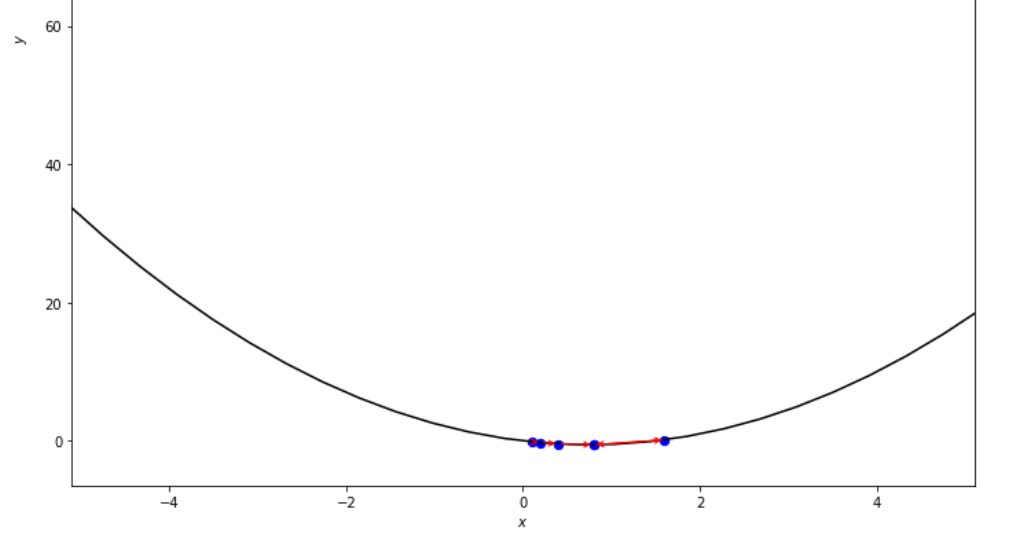
Die Abfolge der Schritte, die der Armijo -Vorwärtsalgorithmus unternommen hat, bevor er das Minimum erreicht
po2 . compare_all_time ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 ) Laufzeit 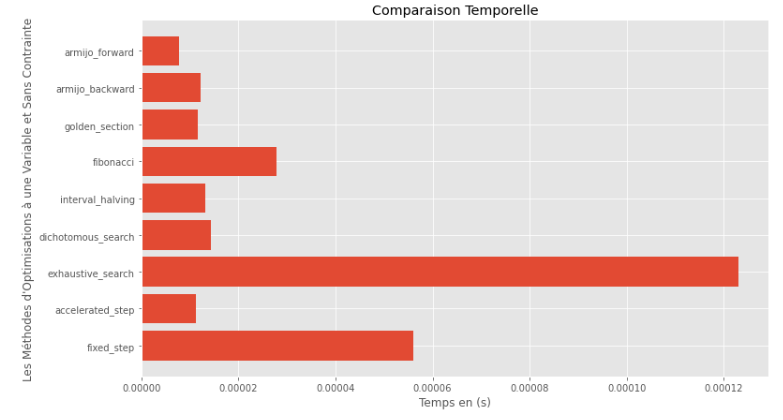
po2 . compare_all_precision ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 ) Kluft zwischen wahrem und berechneten Minimum 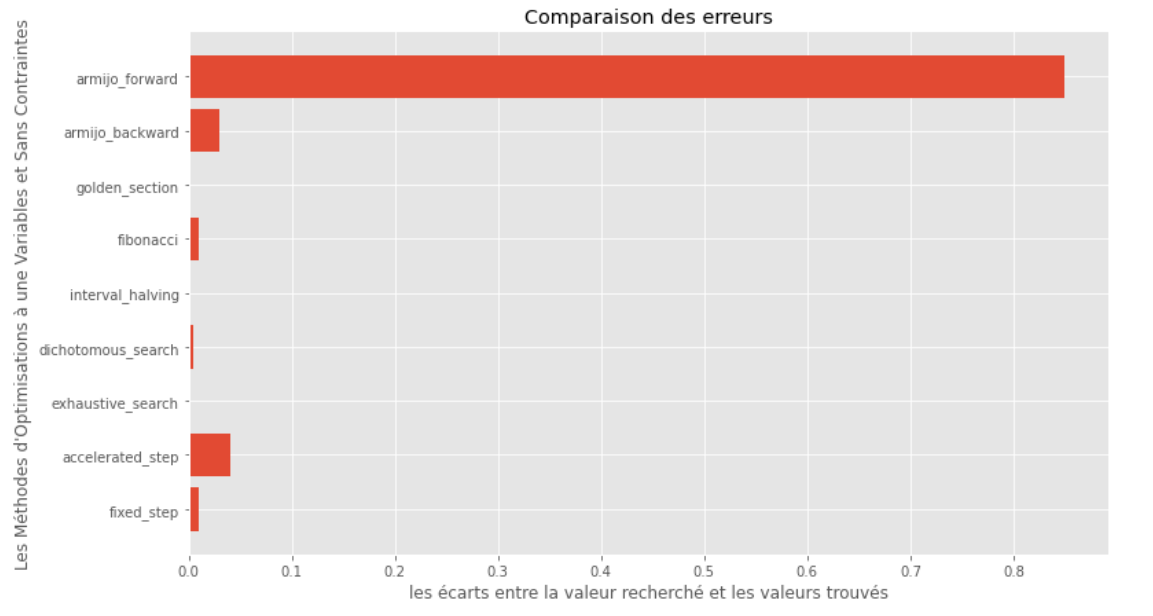
Aus den Laufzeit- und Genauigkeitsgraphen kann abgeleitet werden, dass die für diese konvexe Einzelvariablenfunktion bewertete Algorithmen die goldene Abschnittsmethode als optimale Wahl entsteht und eine Mischung aus hoher Genauigkeit und insbesondere niedriger Laufzeit bietet.
import pyoptim . my_plot . multivar . _3D as pm3
import pyoptim . my_plot . multivar . contour2D as pmc def h ( x ):
return x [ 0 ] - x [ 1 ] + 2 * ( x [ 0 ] ** 2 ) + 2 * x [ 1 ] * x [ 0 ] + x [ 1 ] ** 2
# analytically, argmin(f) = [-1, 1.5]Analitische Lösung
X = [ 1000 , 897 ]
alpha = 1.e-2
tol = 1.e-2 pmc . gradient_descent ( h , X , tol , alpha )
pm3 . gradient_descent ( h , X , tol , alpha ) Y* = [-1.01 1.51] Die Abfolge der Schritte, die der Gradient -Abstiegsalgorithmus unternommen hat 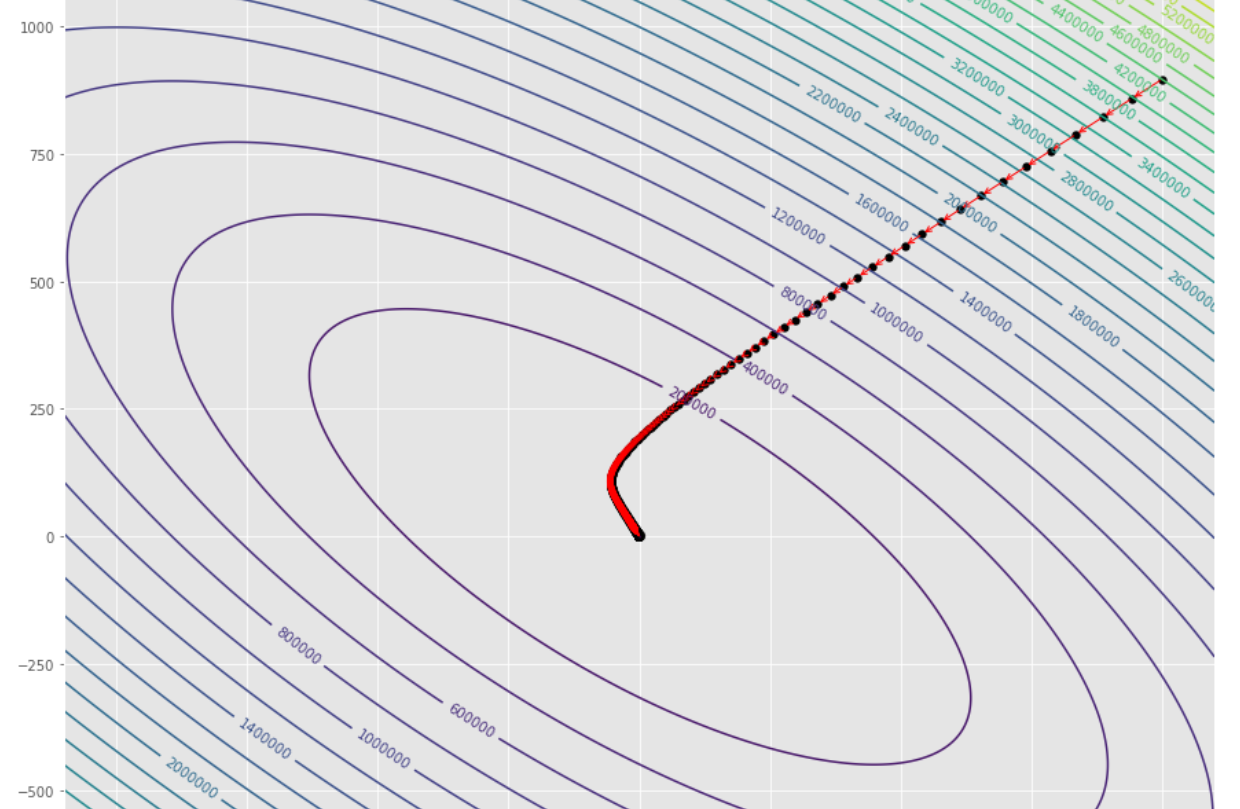
Konturdiagramm 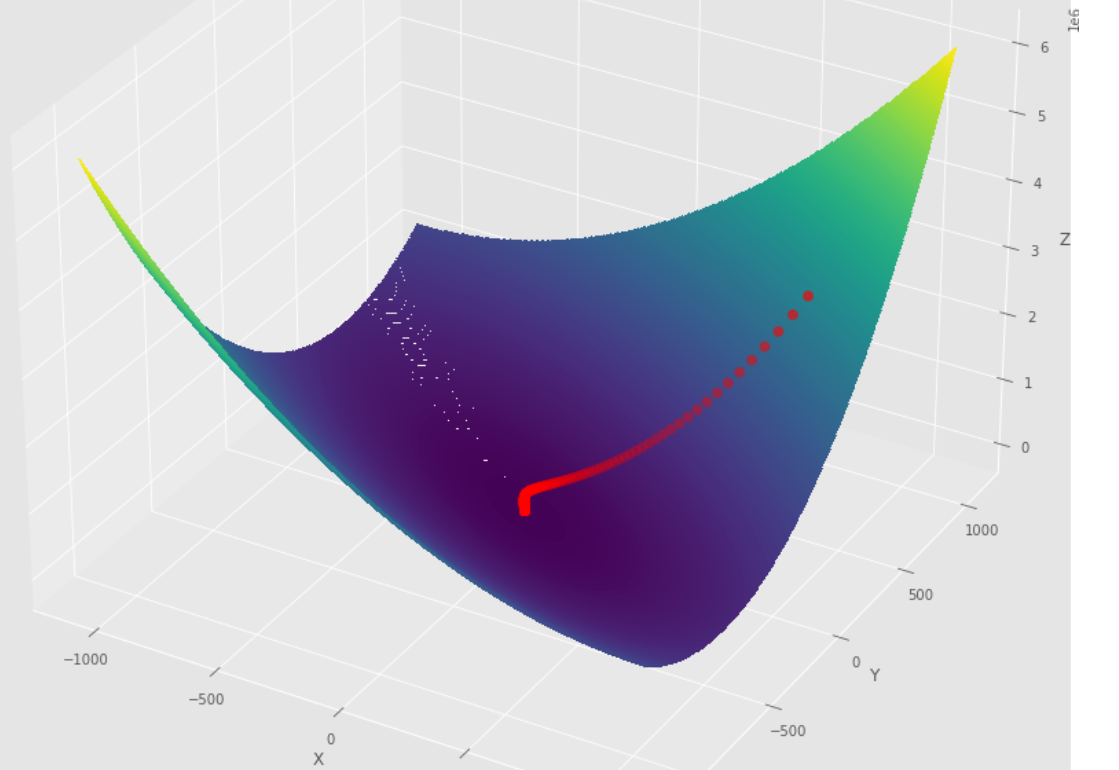
3D -Diagramm
pmc . gradient_conjugate ( h , X , tol )
pm3 . gradient_conjugate ( h , X , tol ) Y* = [-107.38 172.18] Die Abfolge der Schritte, die der Gradienten -Konjugatalgorithmus unternommen hat 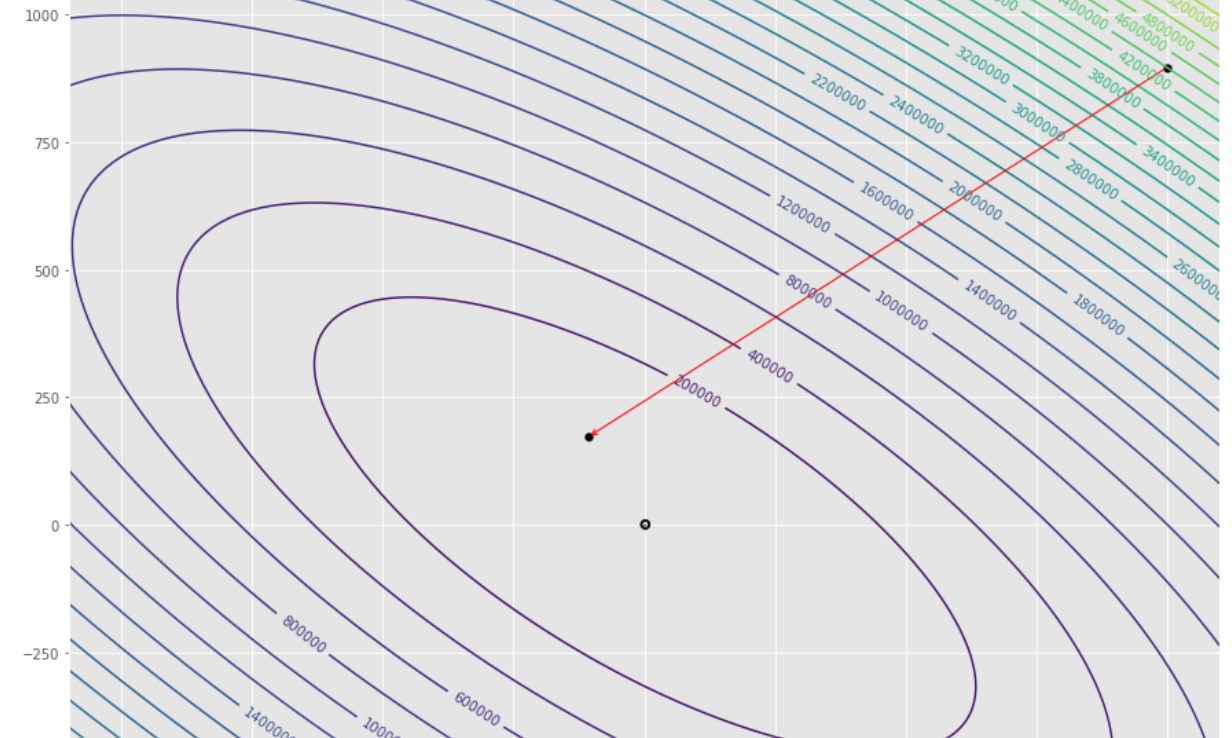
Konturdiagramm 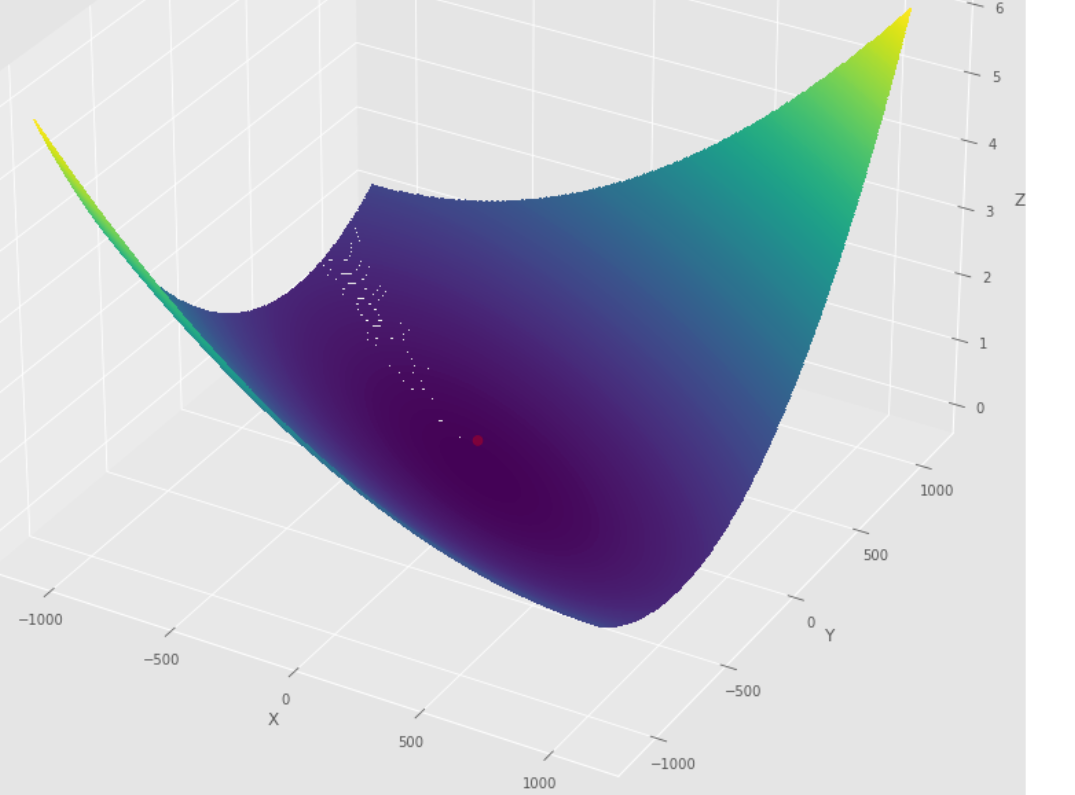
3D -Diagramm
pmc . newton ( h , X , tol )
pm3 . newton ( h , X , tol ) Y* = [-1. 1.5] Die Abfolge der Schritte, die der Newton -Algorithmus unternommen hat, bevor Sie das Minimum erreichen 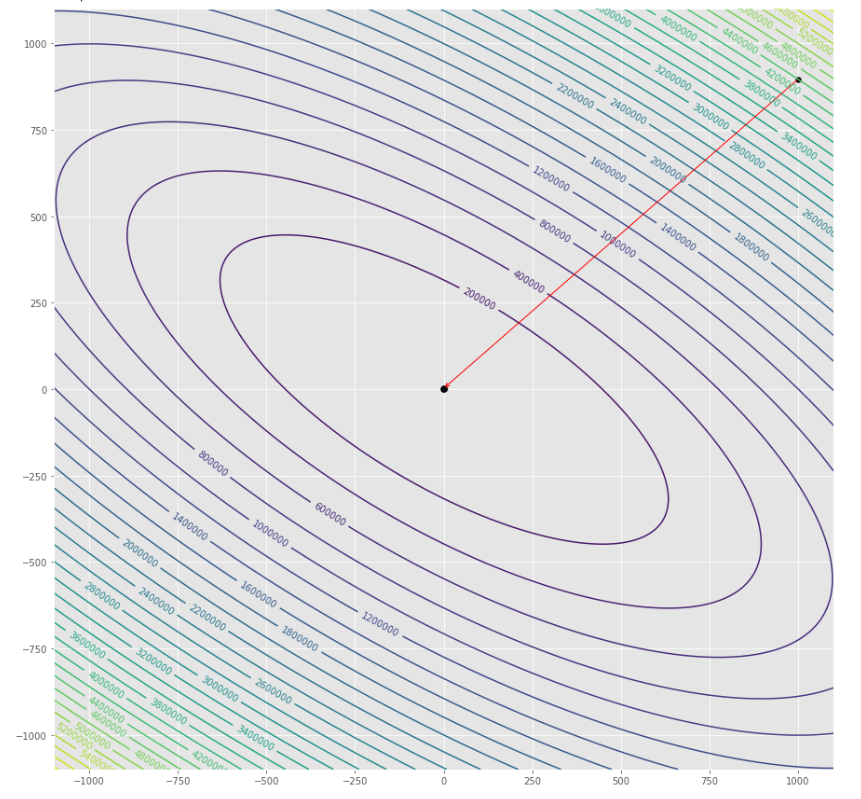
Konturdiagramm 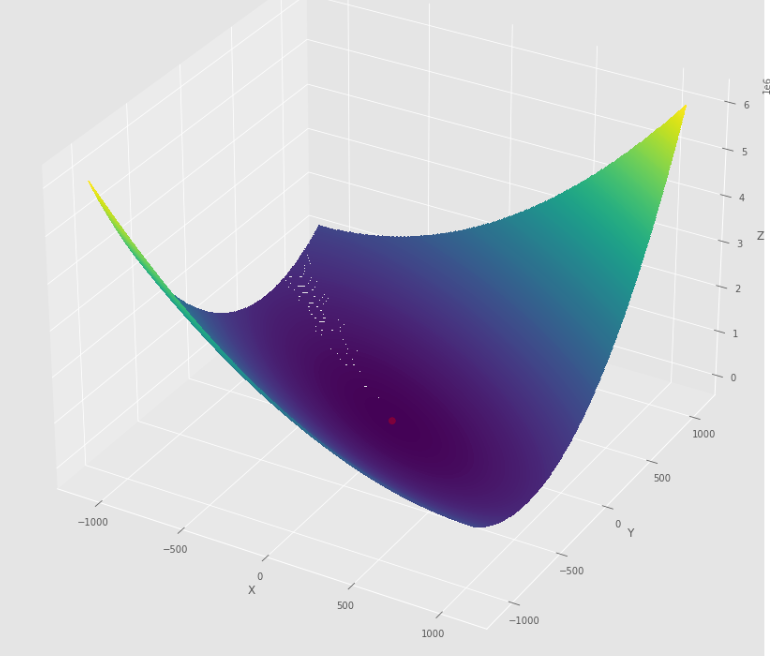
3D -Diagramm
pmc . quasi_newton_dfp ( h , X , tol )
pm3 . quasi_newton_dfp ( h , X , tol ) Y* = [-1. 1.5] Die Abfolge der Schritte des Quasi Newton DFP -Algorithmus, bevor Sie das Minimum erreichen 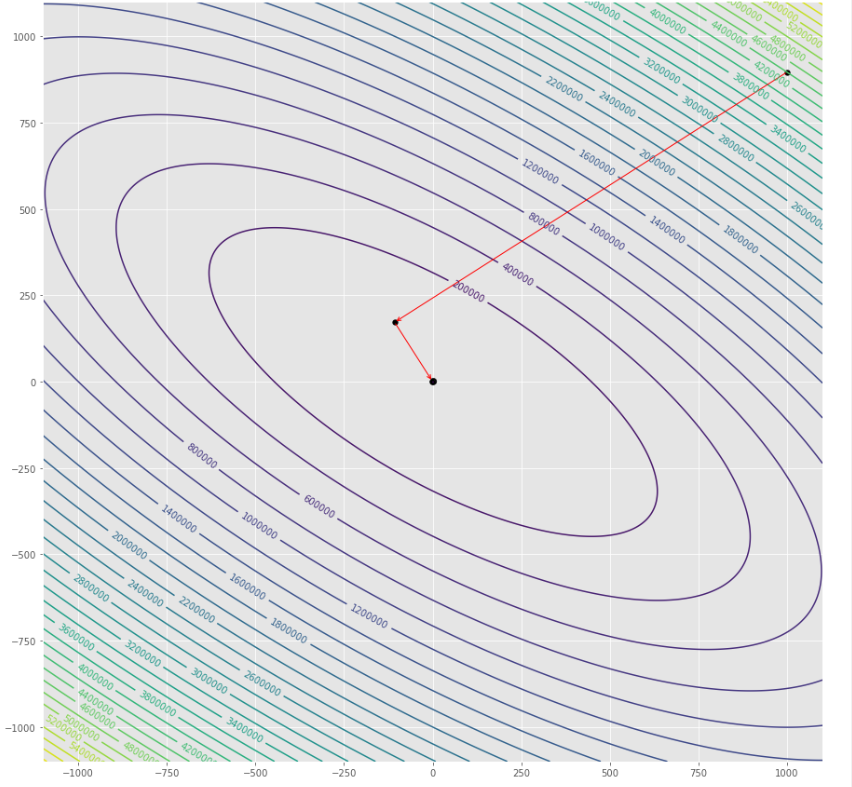
Konturdiagramm 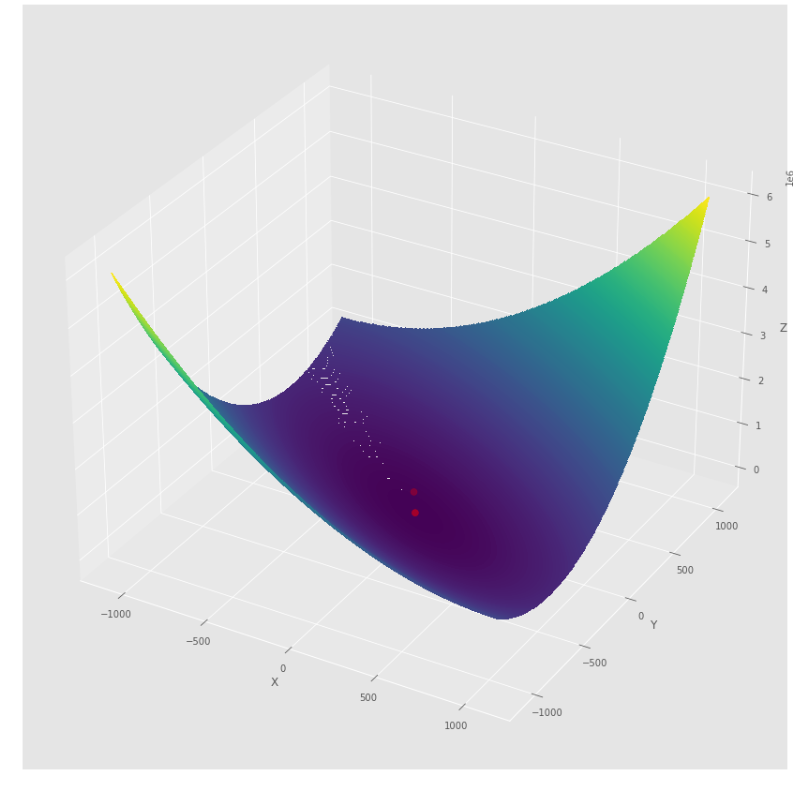
3D -Diagramm
pmc . sgd ( h , X , tol , alpha )
pm3 . sgd ( h , X , tol , alpha ) Y* = [-1.01 1.52] Die Folge der Schritte, 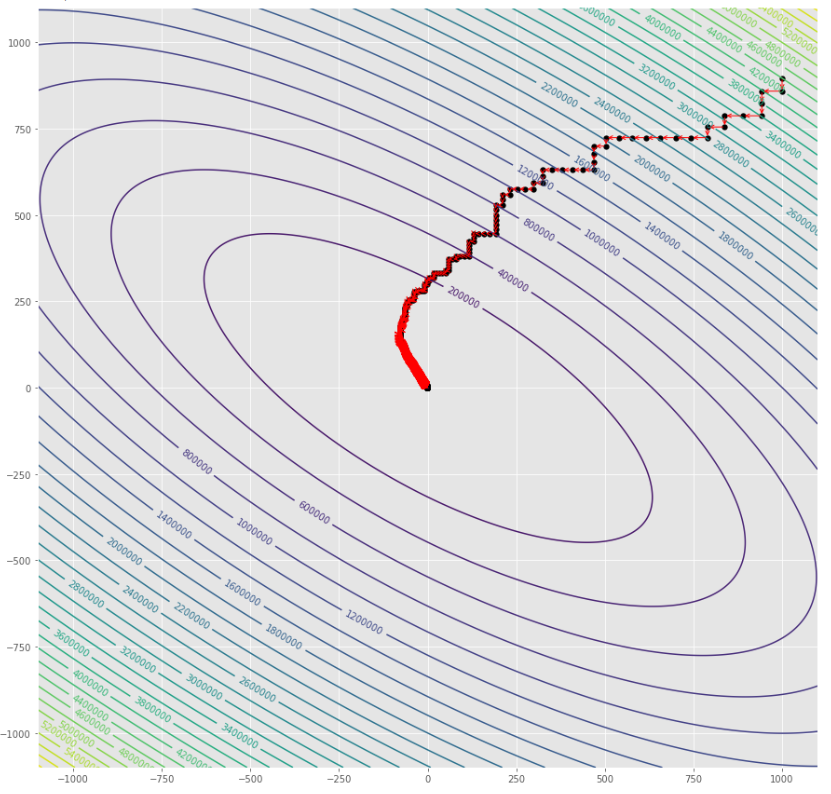
Konturdiagramm 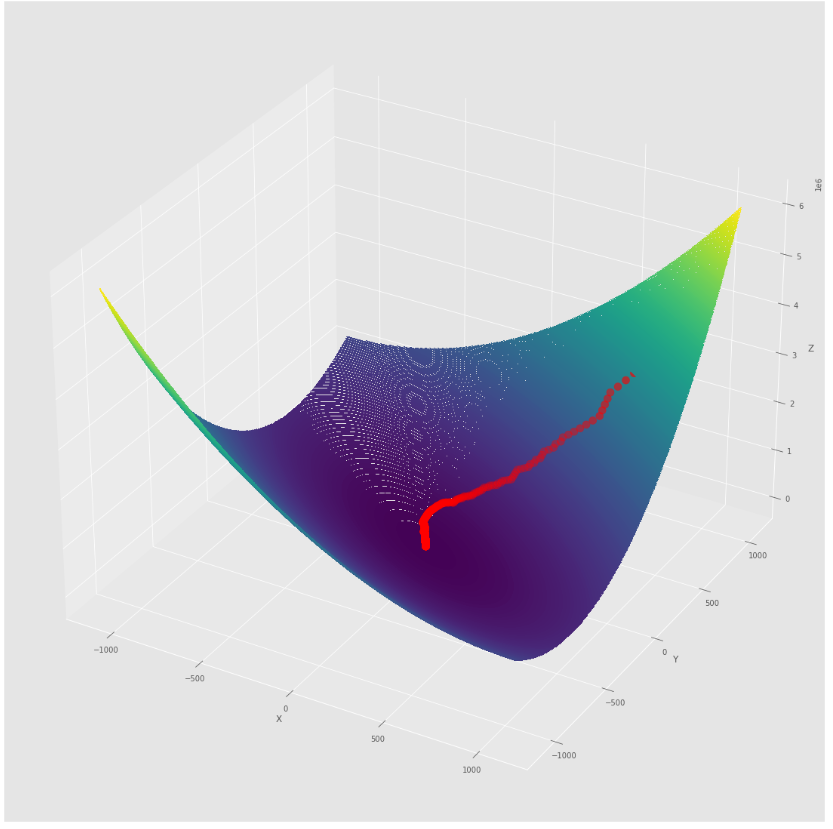
3D -Diagramm
alpha = 100 #it must be high because of BLS
c = 2
pmc . sgd_with_bls ( h , X , tol , alpha , c )
pm3 . sgd_with_bls ( h , X , tol , alpha , c ) Y* = [-1. 1.5] Die Folge von Schritten, 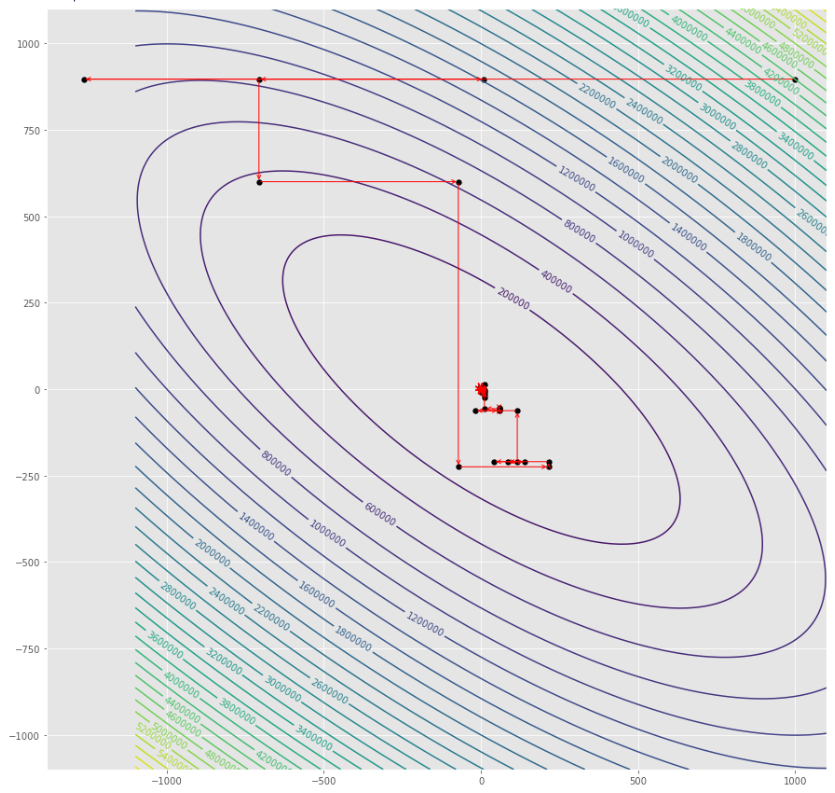
Konturdiagramm 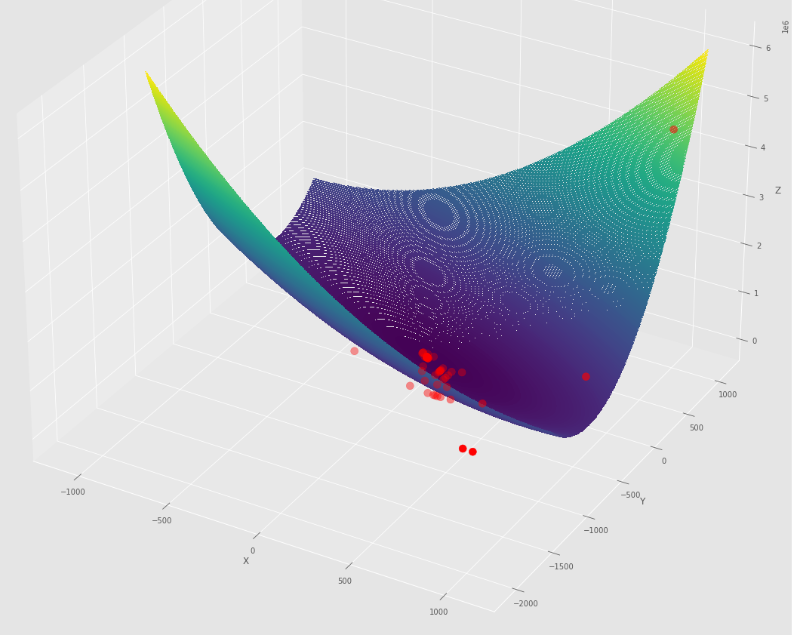
3D -Diagramm
pm3 . compare_all_time ( h , X , 1.e-2 , 1.e-1 , 100 , 2 ) Laufzeit 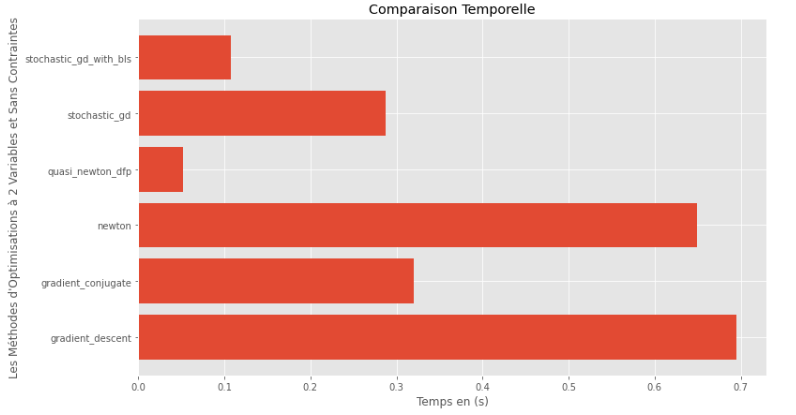
pm3 . compare_all_precision ( h , X , 1.e-2 , 1.e-1 , 100 , 2 ) Kluft zwischen wahrem und berechneten Minimum 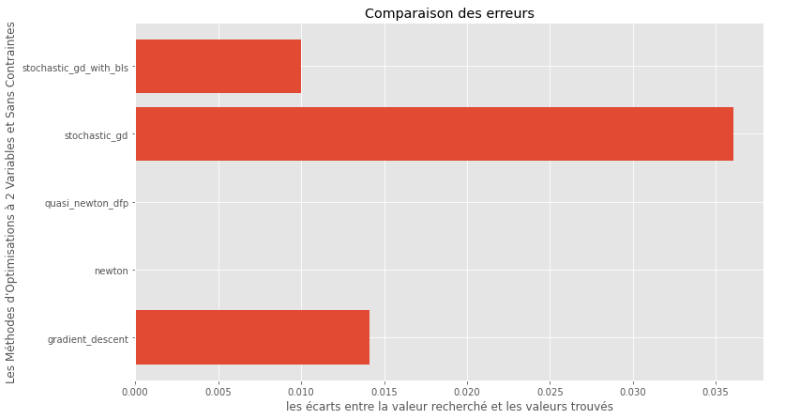
Aus den Graphen der Laufzeit und der Genauigkeit kann abgeleitet werden, dass die für diese konvexe multivariablen Funktion bewertete Algorithmen die quasi Newton -DFP -Methode als optimale Wahl entsteht und eine Mischung aus hoher Genauigkeit und besonders niedriger Laufzeit bietet.
import pyoptim . my_numpy . inverse as npi 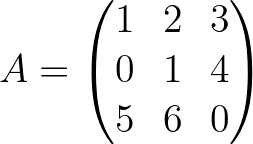
A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]]) A_1 = npi . gaussjordan ( A . copy ())
I = A @ A_1
I = np . around ( I , 1 )
print ( 'A_1 = n n ' , A_1 )
print ( ' n A_1*A = n n ' , I ) A_1 =
[[-24. 18. 5.]
[ 20. -15. -4.]
[ -5. 4. 1.]]
A_1*A =
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]] import pyoptim . my_numpy . decompose as npd A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]]) #A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ],[ - 1. , 2. , - 1. ],[ 0. , - 1. , 2. ]]) #B is positive definite
Y = np . array ([ 45 , - 78 , 95 ]) #randomly chosen column vector L , U , P = npd . LU ( A )
print ( "P = n " , P , " n n L = n " , L , " n n U = n " , U )
print ( " n " , A == P @ L @ U ) P =
[[0. 0. 1.]
[0. 1. 0.]
[1. 0. 0.]]
L =
[[1. 0. 0. ]
[0. 1. 0. ]
[0.2 0.8 1. ]]
U =
[[ 5. 6. 0. ]
[ 0. 1. 4. ]
[ 0. 0. -0.2]]
[[ True True True]
[ True True True]
[ True True True]] L = npd . choleski ( A ) # A is not positive definite
print ( L )
print ( "--------------------------------------------------" )
L = npd . choleski ( B ) # B is positive definite
print ( 'L = n ' , L , ' n ' )
C = np . around ( L @( L . T ), 1 )
print ( 'B = L@(L.T) n n ' , B == C ) A must be positive definite !
None
--------------------------------------------------
L =
[[ 1.41421356 0. 0. ]
[-0.70710678 1.22474487 0. ]
[ 0. -0.81649658 1.15470054]]
B = L@(L.T)
[[ True True True]
[ True True True]
[ True True True]] import pyoptim . my_numpy . solve as nps 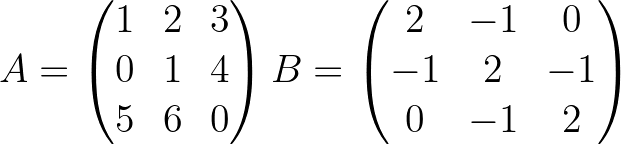
A = np . array ([[ 1. , 2. , 3. ], [ 0. , 1. , 4. ], [ 5. , 6. , 0. ]]) # A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ], [ - 1. , 2. , - 1. ], [ 0. , - 1. , 2. ]]) # B is positive definite
Y = np . array ([ 45 , - 78 , 95 ]) # randomly chosen column vector X = nps . gaussjordan ( A , Y )
print ( "X = n " , X )
print ( " n A@X=Y n " , A @ X == Y , ' n ' )
print ( '---------------------------------------------------------------' )
X = nps . gaussjordan ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n B@X=Y n " , Y_ == Y , ' n ' ) X =
[[-2009.]
[ 1690.]
[ -442.]]
A@X=Y
[[ True]
[ True]
[ True]]
---------------------------------------------------------------
X =
[[18.5]
[-8. ]
[43.5]]
B@X=Y
[[ True]
[ True]
[ True]]
X = nps . LU ( A , Y )
print ( "X* = n " , X )
print ( " n AX*=Y n " , A @ X == Y )
print ( "-------------------------------------------------------------------------------" );
X = nps . LU ( B , Y )
print ( "X* = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y ) X* =
[[-2009.]
[ 1690.]
[ -442.]]
AX*=Y
[[ True]
[ True]
[ True]]
-------------------------------------------------------------------------------
X* =
[[18.5]
[-8. ]
[43.5]]
BX*=Y
[[ True]
[ True]
[ True]] X = nps . choleski ( A , Y )
print ( "-------------------------------------------------------------------------------" )
X = nps . choleski ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y ) !! A must be positive definite !!
-------------------------------------------------------------------------------
X =
[[18.5]
[-8. ]
[43.5]]
BX*=Y
[[ True]
[ True]
[ True]]