Pyoptim: paquete Python para optimización y operaciones de matriz
Este proyecto, un componente del curso de análisis y optimización numéricos en Asias, la Universidad Mohammed V surgió de la sugerencia del profesor M. Naoum de crear un paquete de pitón que encapsule algoritmos practicados durante las sesiones de laboratorio. Se centra en aproximadamente diez algoritmos de optimización sin restricciones, que ofrecen visualizaciones 2D y 3D, lo que permite una comparación de rendimiento en la eficiencia y precisión computacionales. Además, el proyecto abarca operaciones de matriz como inversión, descomposición y resolución de sistemas lineales, todos integrados dentro del paquete que contiene los algoritmos derivados de laboratorio.
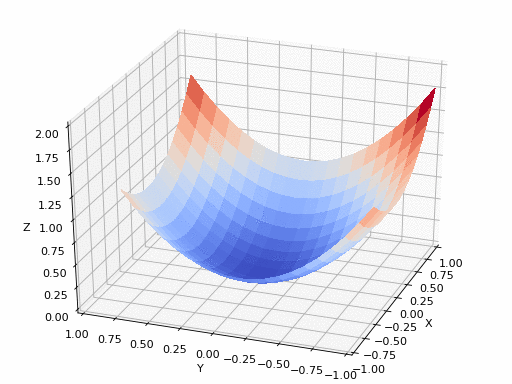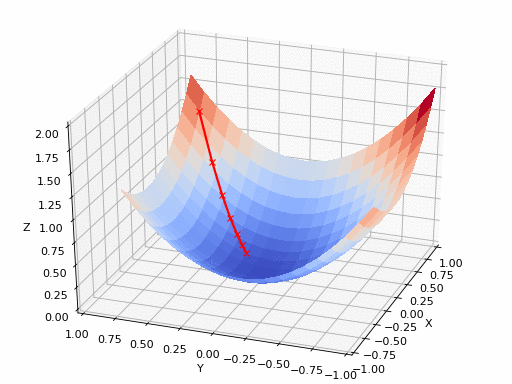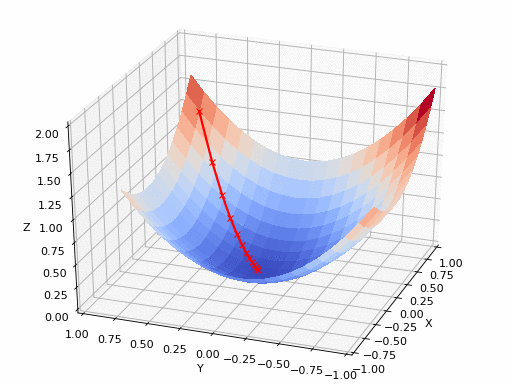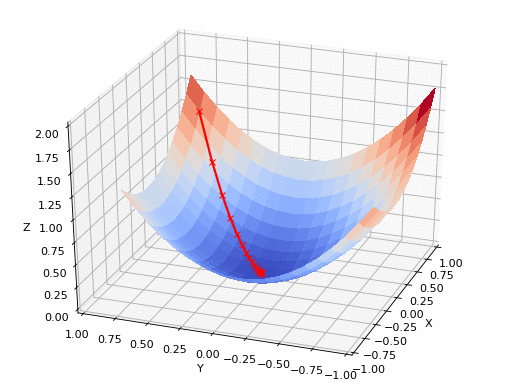
GIF Fuente: https://www.nsf.gov/news/mmg/mmg_disp.jsp?med_id=78950&from=font>(https://aria42.com/blog/2014/12/understanding-lbfgs
Cada parte de este proyecto es el código de muestra que muestra cómo hacer lo siguiente:
Implementación de algoritmos de optimización une variable, que abarcan fijado_step, acelerado_step, exhaustive_search, dicotomous_search, interval_halving, fibonacci, dorado_section, armijo_backward y armijo_forward.
Incorporación de varios algoritmos de optimización de una variable, incluyendo descenso de gradiente, conjugado de gradiente, Newton, cuasi_newton_dfp, descenso de gradiente estocástico.
Visualización de cada paso de iteración para todos los algoritmos en formatos 2D, contornos y 3D.
Realizar un análisis comparativo centrado en su tiempo de ejecución y métricas de precisión.
Implementación de operaciones de matriz como inversión (p. Ej., Gauss-Jordan), descomposición (p. Ej., Lu, Choleski) y soluciones para sistemas lineales (por ejemplo, Gauss-Jordan, Lu, Choleski).
Para instalar este paquete Python:
pip install pyoptimEjecute este cuaderno de demostración
import pyoptim . my_scipy . onevar_optimize . minimize as soom
import pyoptim . my_plot . onevar . _2D as po2 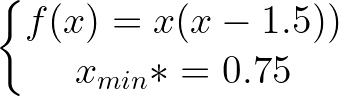
def f ( x ):
return x * ( x - 1.5 ) # analytically, argmin(f) = 0.75 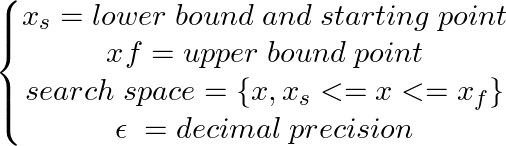
xs = - 10
xf = 10
epsilon = 1.e-2 print ( 'x* =' , soom . fixed_step ( f , xs , epsilon ))
po2 . fixed_step ( f , xs , epsilon ) x* = 0.75 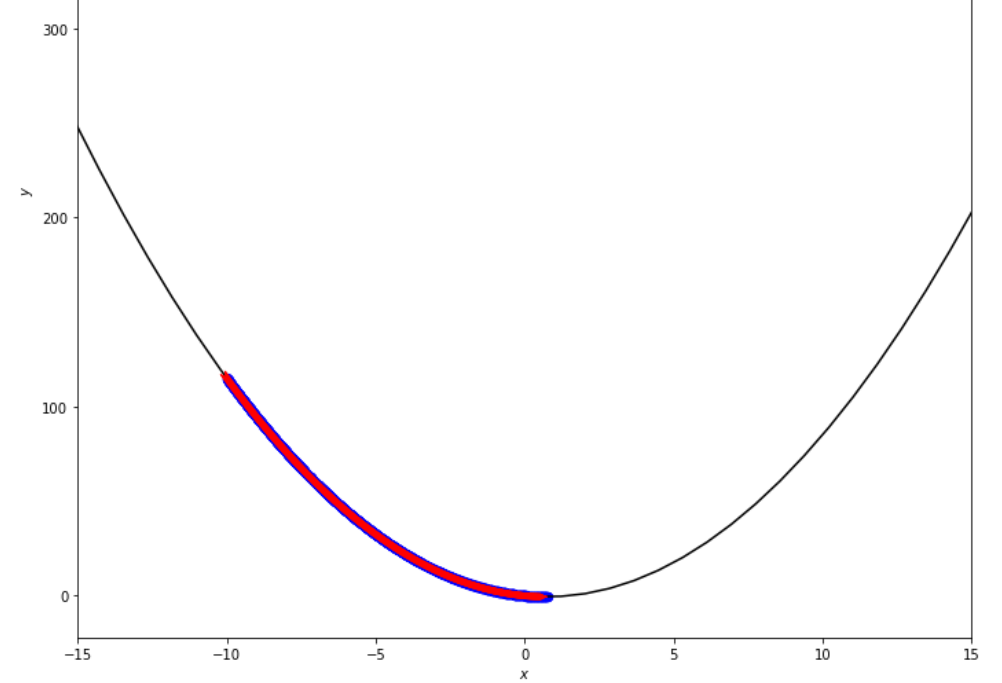
La secuencia de pasos dados por el algoritmo de paso fijo antes de alcanzar el mínimo
print ( 'x* =' , soom . accelerated_step ( f , xs , epsilon ))
po2 . accelerated_step ( f , xs , epsilon ) x* = 0.86 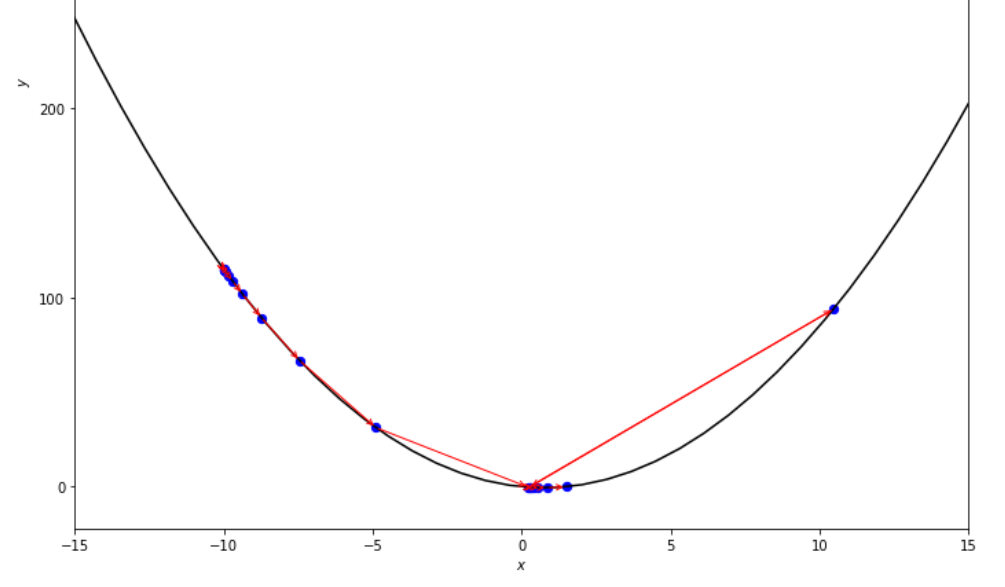
La secuencia de pasos dados por el algoritmo de paso acelerado antes de alcanzar el mínimo
print ( 'x* =' , soom . exhaustive_search ( f , xs , xf , epsilon ))
po2 . exhaustive_search ( f , xs , xf , epsilon ) x* = 0.75
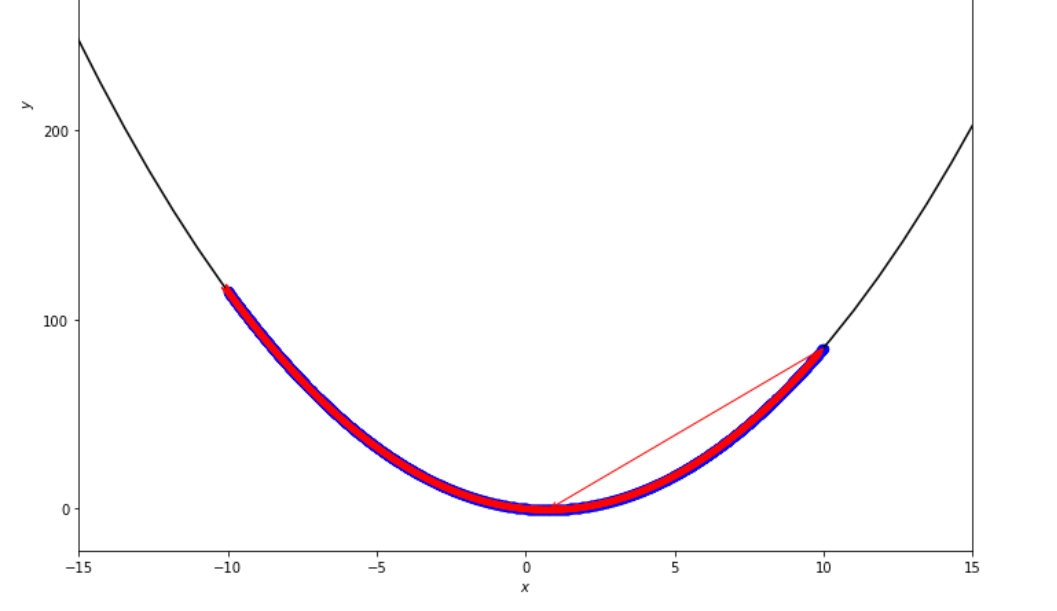
La secuencia de pasos dados por el algoritmo de búsqueda exhaustivo antes de alcanzar el mínimo
mini_delta = 1.e-3
print ( 'x* =' , soom . dichotomous_search ( f , xs , xf , epsilon , mini_delta ))
po2 . dichotomous_search ( f , xs , xf , epsilon , mini_delta ) x* = 0.7494742431640624
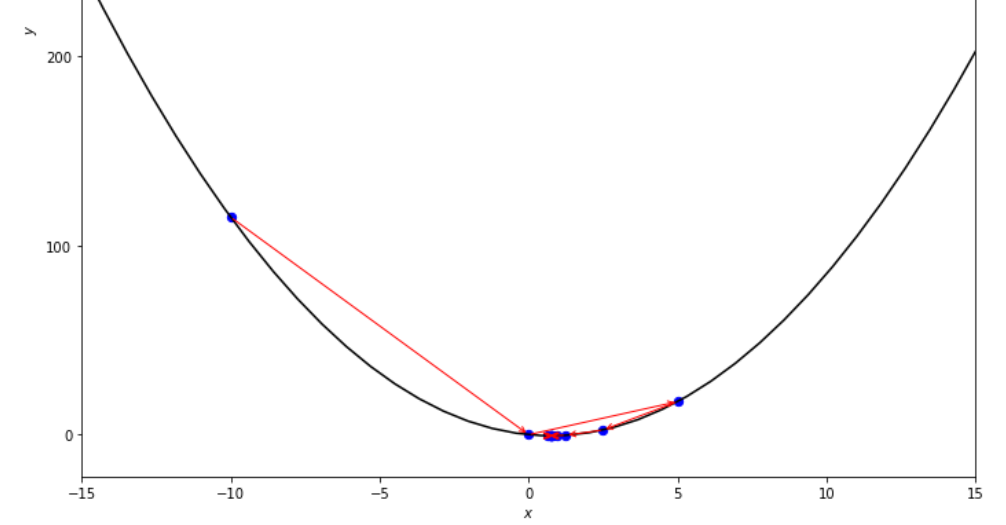
La secuencia de pasos dados por el algoritmo de búsqueda dicotómica antes de alcanzar el mínimo
print ( 'x* =' , soom . interval_halving ( f , xs , xf , epsilon ))
po2 . interval_halving ( f , xs , xf , epsilon ) x* = 0.75
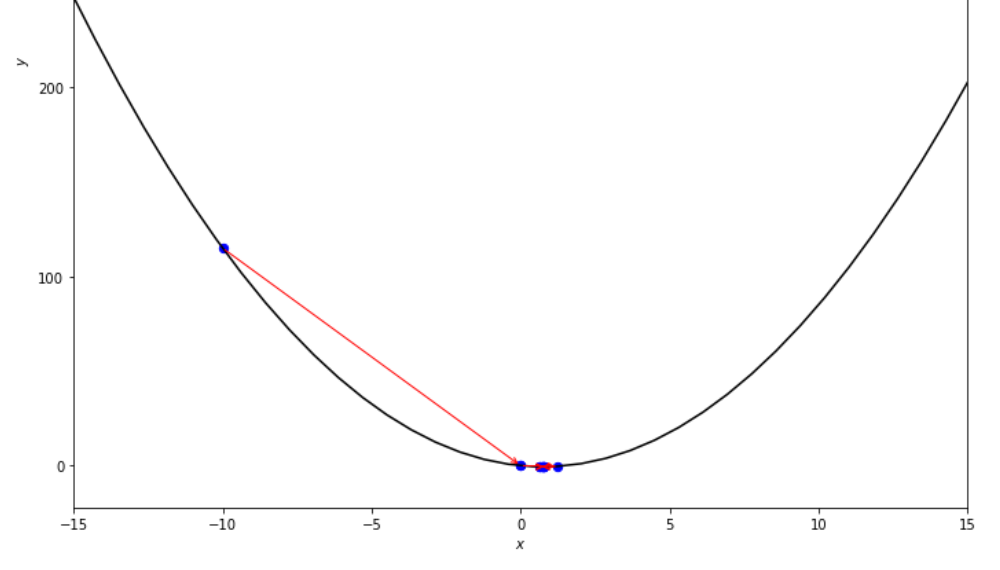
La secuencia de pasos tomados por el algoritmo de mitad de intervalo antes de alcanzar el mínimo.
n = 15
print ( 'x* =' , soom . fibonacci ( f , xs , xf , n ))
po2 . fibonacci ( f , xs , xf , n ) x* = 0.76 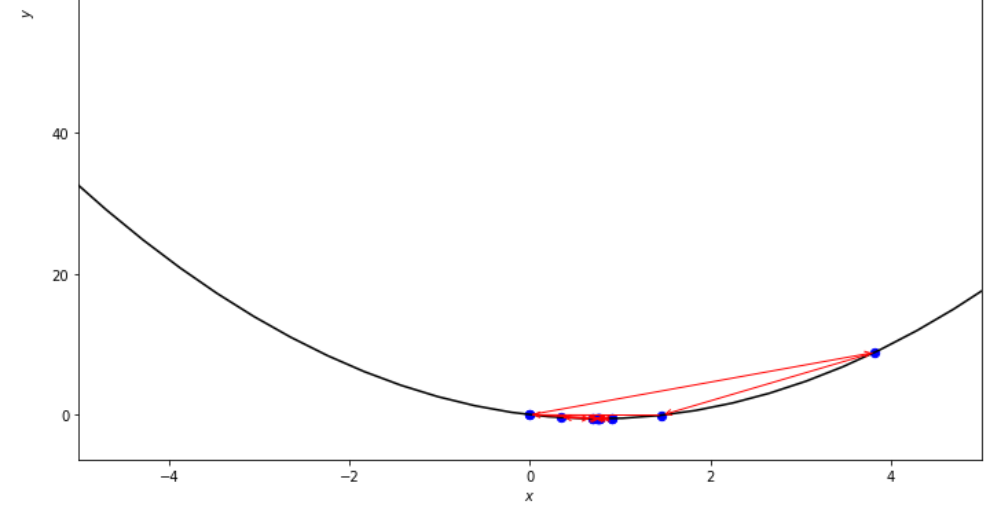
La secuencia de pasos dados por el algoritmo Fibonacci antes de alcanzar el mínimo.
print ( 'x* =' , soom . golden_section ( f , xs , xf , epsilon ))
po2 . golden_section ( f , xs , xf , epsilon ) x* = 0.75 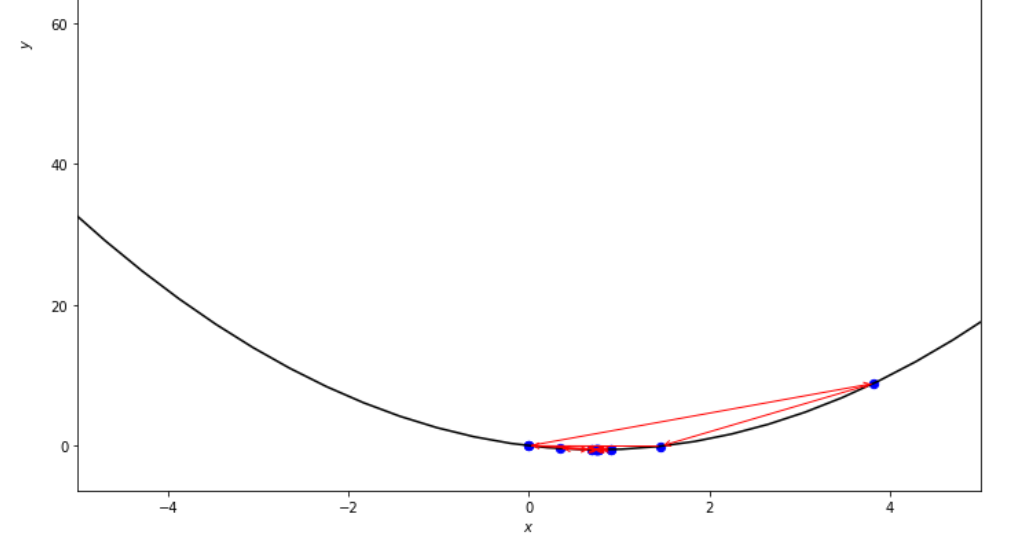
La secuencia de pasos dados por el algoritmo de la sección dorada antes de alcanzar el mínimo
ŋ = 2
xs = 100
print ( 'x* =' , soom . armijo_backward ( f , xs , ŋ , epsilon ))
po2 . armijo_backward ( f , xs , ŋ , epsilon ) x* = 0.78 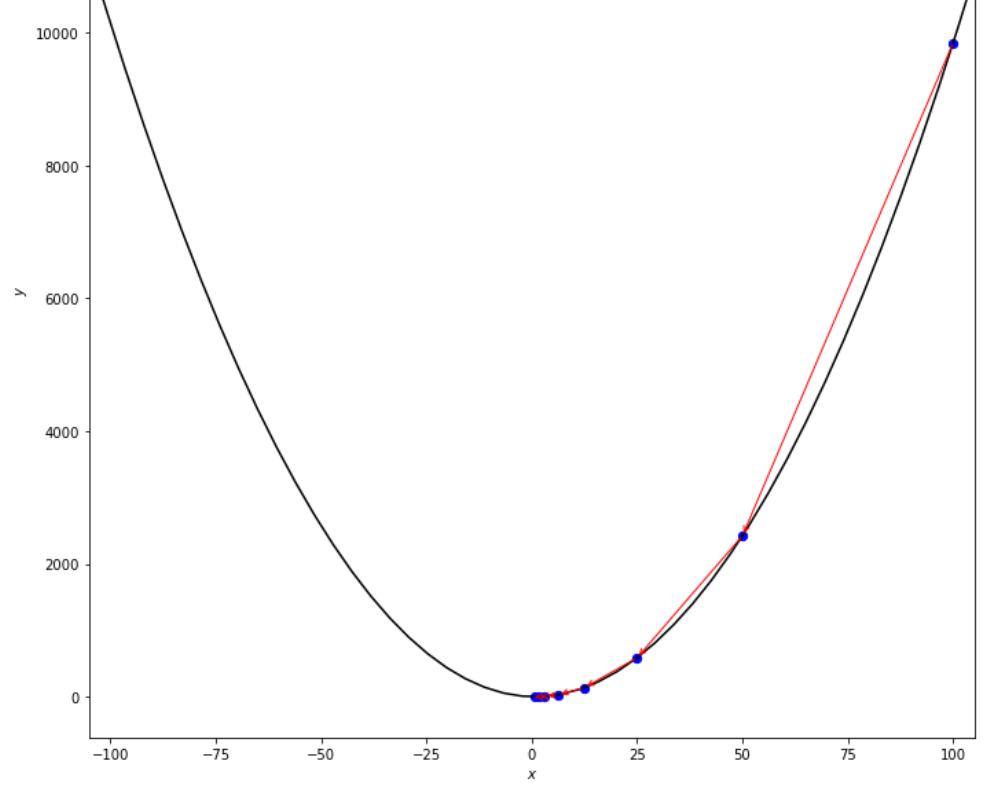
La secuencia de pasos dados por el algoritmo hacia atrás de Armijo ANTER ANTES de alcanzar el mínimo
xs = 0.1
epsilon = 0.5
ŋ = 2
print ( 'x* =' , soom . armijo_forward ( f , xs , ŋ , epsilon ))
po2 . armijo_forward ( f , xs , ŋ , epsilon ) x* = 0.8 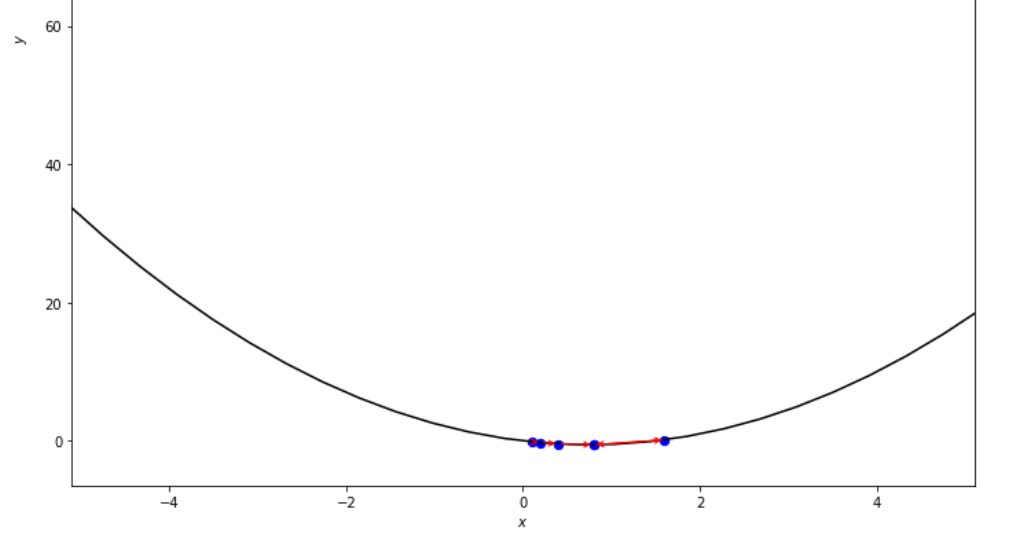
La secuencia de pasos dados por el algoritmo de avance de Armijo antes de alcanzar el mínimo
po2 . compare_all_time ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 ) Tiempo de ejecución 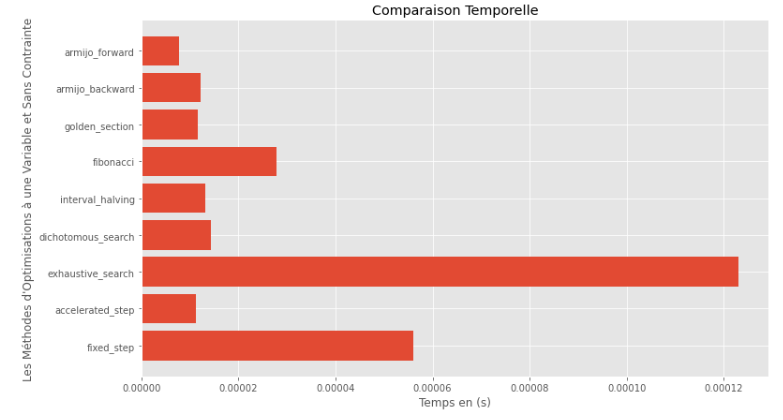
po2 . compare_all_precision ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 ) Brecha entre mínimo verdadero y calculado 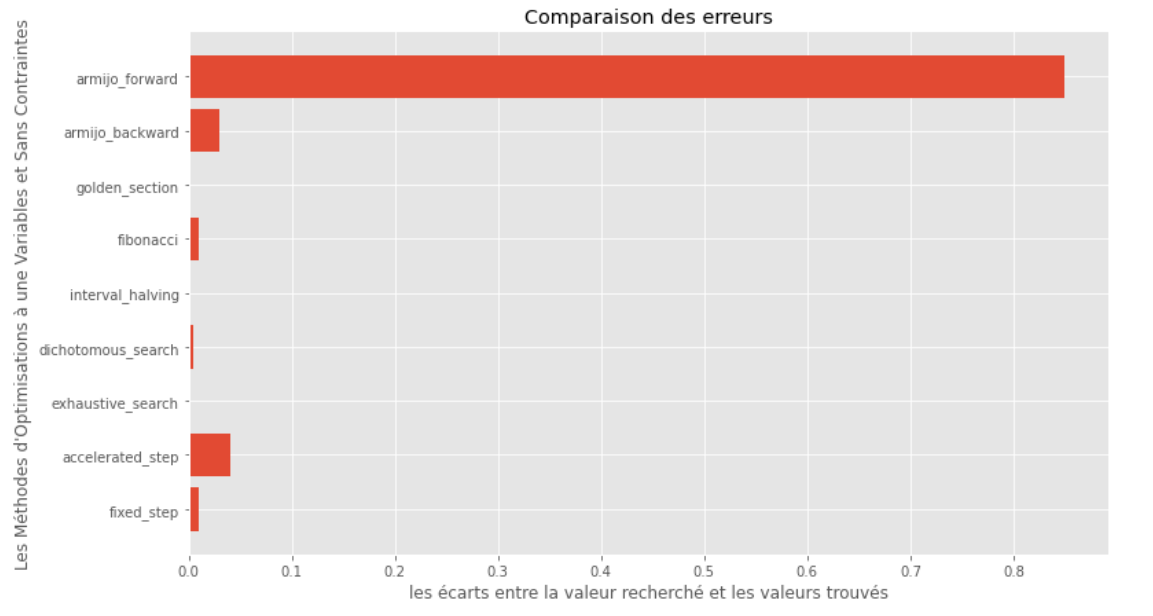
Desde el tiempo de ejecución y los gráficos de precisión, se puede deducir que entre los algoritmos evaluados para esta función de variable única convexa, el método de la sección dorada surge como la opción óptima, ofreciendo una combinación de alta precisión y un tiempo de ejecución notablemente bajo.
import pyoptim . my_plot . multivar . _3D as pm3
import pyoptim . my_plot . multivar . contour2D as pmc def h ( x ):
return x [ 0 ] - x [ 1 ] + 2 * ( x [ 0 ] ** 2 ) + 2 * x [ 1 ] * x [ 0 ] + x [ 1 ] ** 2
# analytically, argmin(f) = [-1, 1.5]solución analítica
X = [ 1000 , 897 ]
alpha = 1.e-2
tol = 1.e-2 pmc . gradient_descent ( h , X , tol , alpha )
pm3 . gradient_descent ( h , X , tol , alpha ) Y* = [-1.01 1.51] La secuencia de pasos dados por el algoritmo de descenso de gradiente antes de alcanzar el mínimo 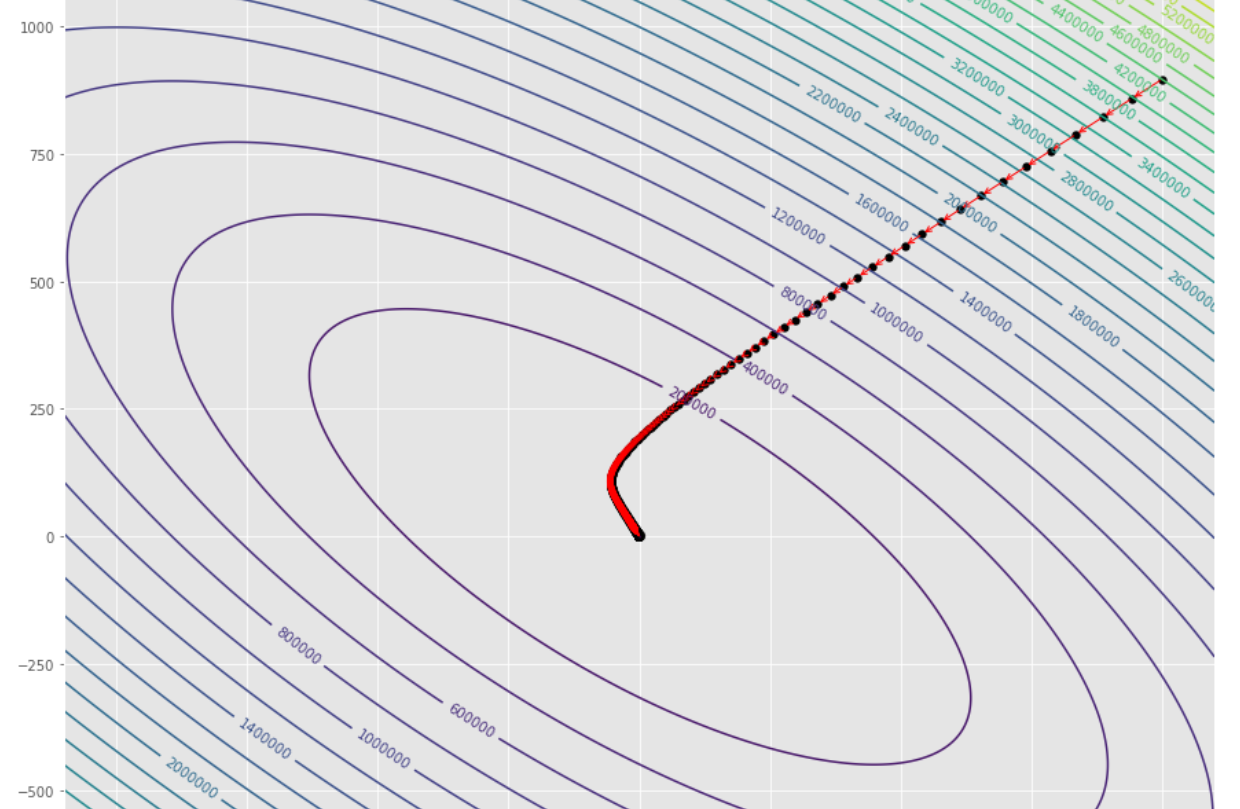
Trama de contorno 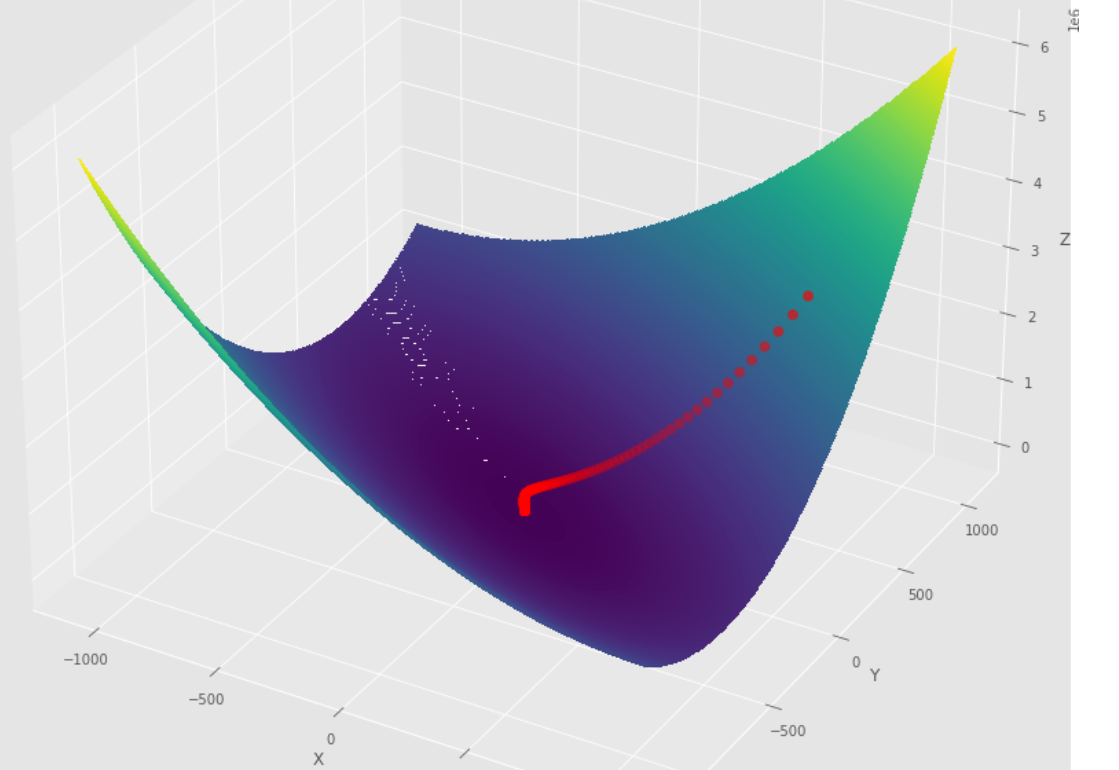
Trama 3D
pmc . gradient_conjugate ( h , X , tol )
pm3 . gradient_conjugate ( h , X , tol ) Y* = [-107.38 172.18] La secuencia de pasos dados por el algoritmo de conjugado de gradiente antes de alcanzar el mínimo 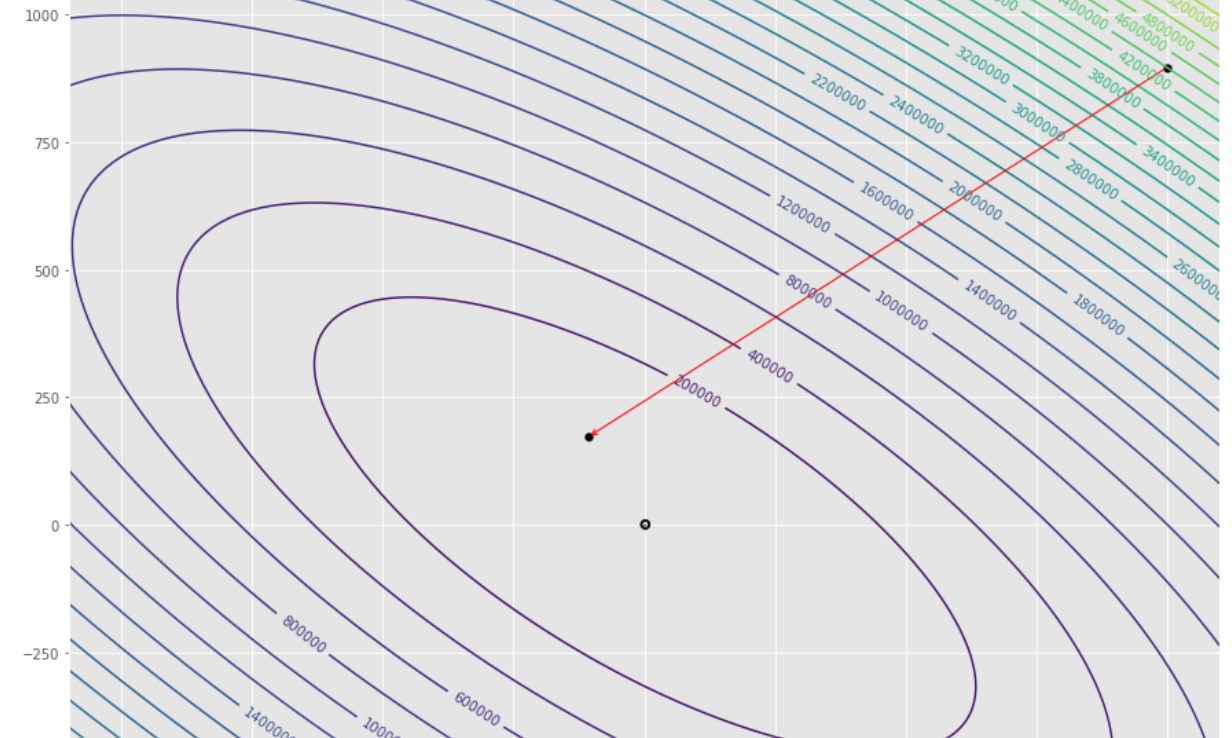
Trama de contorno 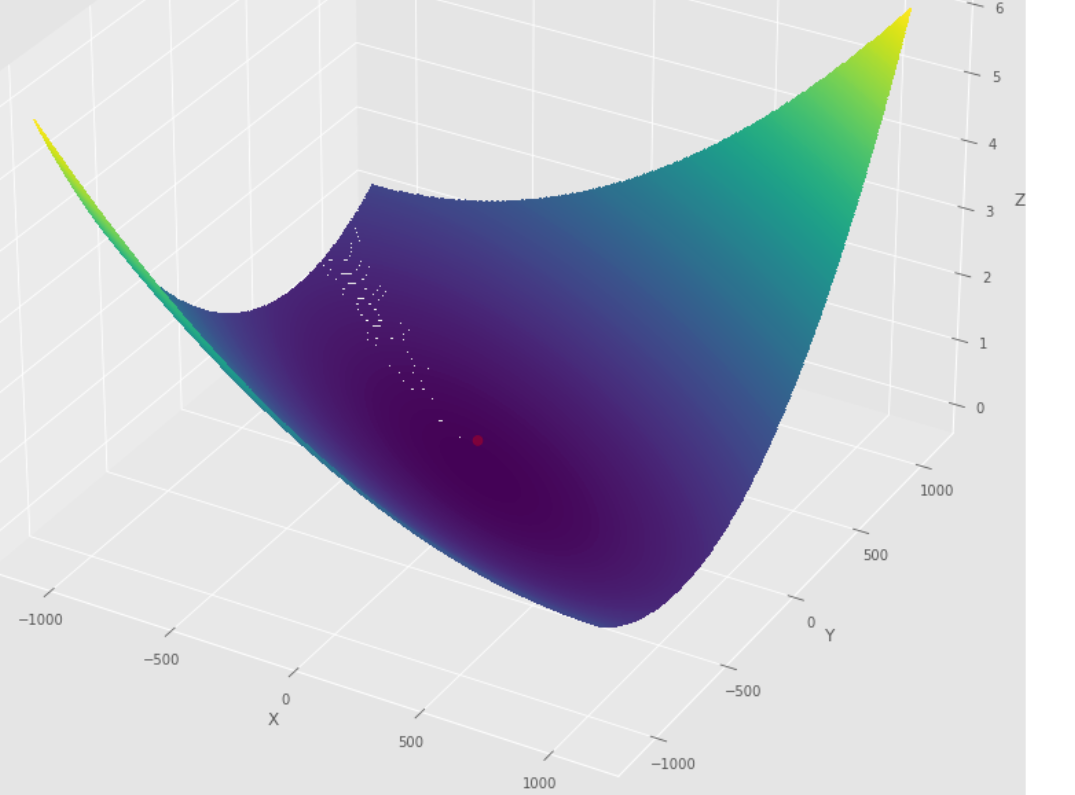
Trama 3D
pmc . newton ( h , X , tol )
pm3 . newton ( h , X , tol ) Y* = [-1. 1.5] La secuencia de pasos dados por el algoritmo Newton antes de alcanzar el mínimo 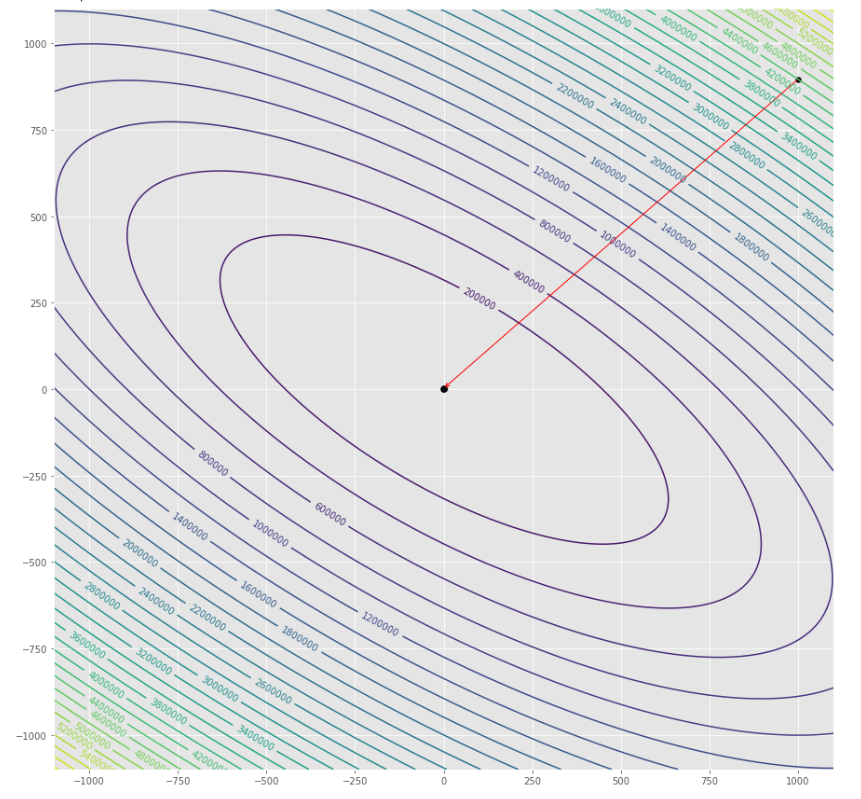
Trama de contorno 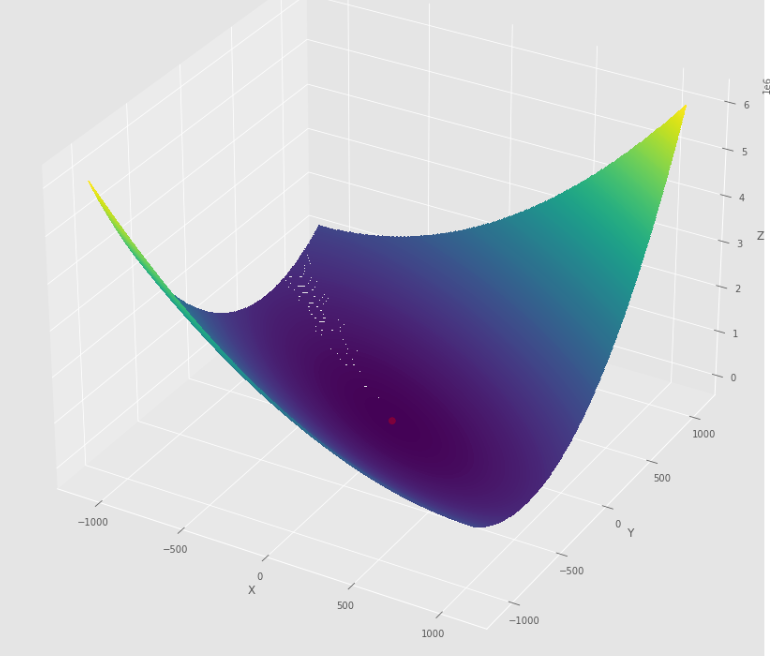
Trama 3D
pmc . quasi_newton_dfp ( h , X , tol )
pm3 . quasi_newton_dfp ( h , X , tol ) Y* = [-1. 1.5] La secuencia de pasos dados por el algoritmo DFP cuasi Newton antes de alcanzar el mínimo 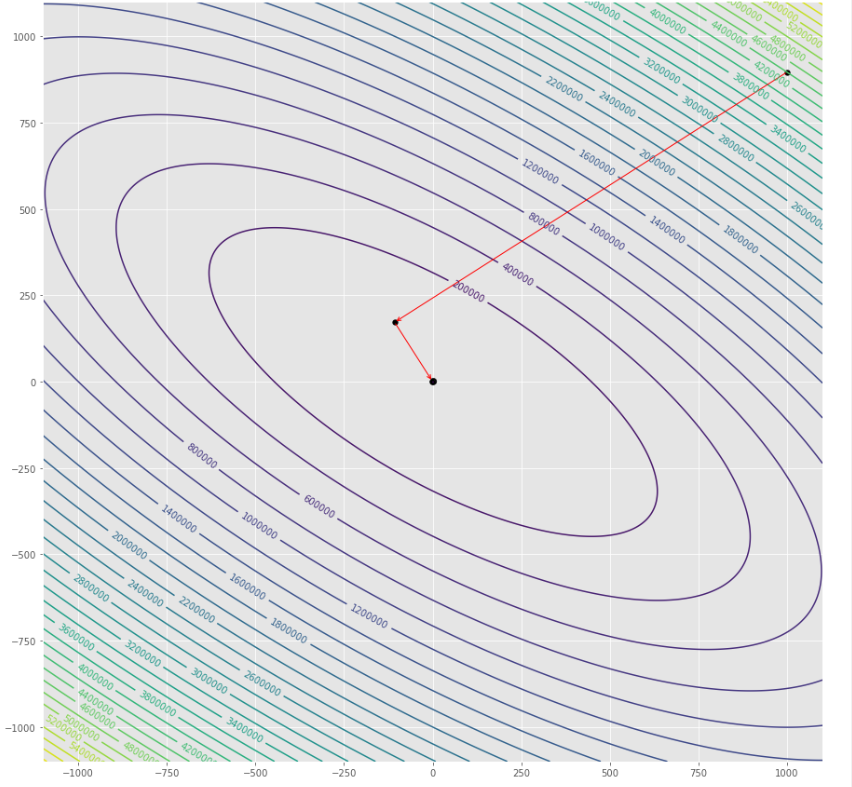
Trama de contorno 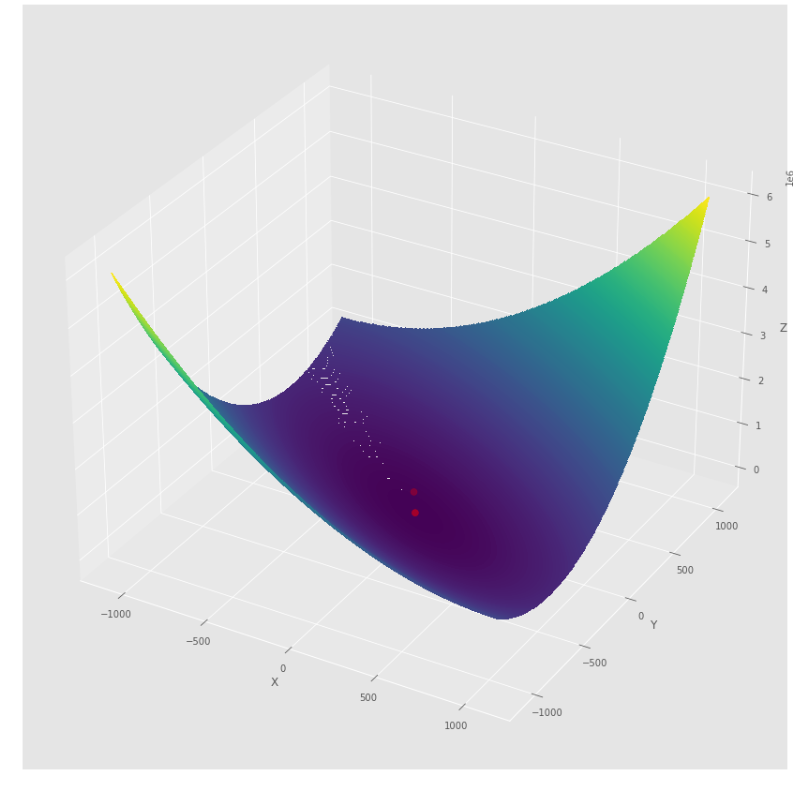
Trama 3D
pmc . sgd ( h , X , tol , alpha )
pm3 . sgd ( h , X , tol , alpha ) Y* = [-1.01 1.52] La secuencia de pasos dados por el algoritmo de descenso de gradiente estocástico antes de alcanzar el mínimo 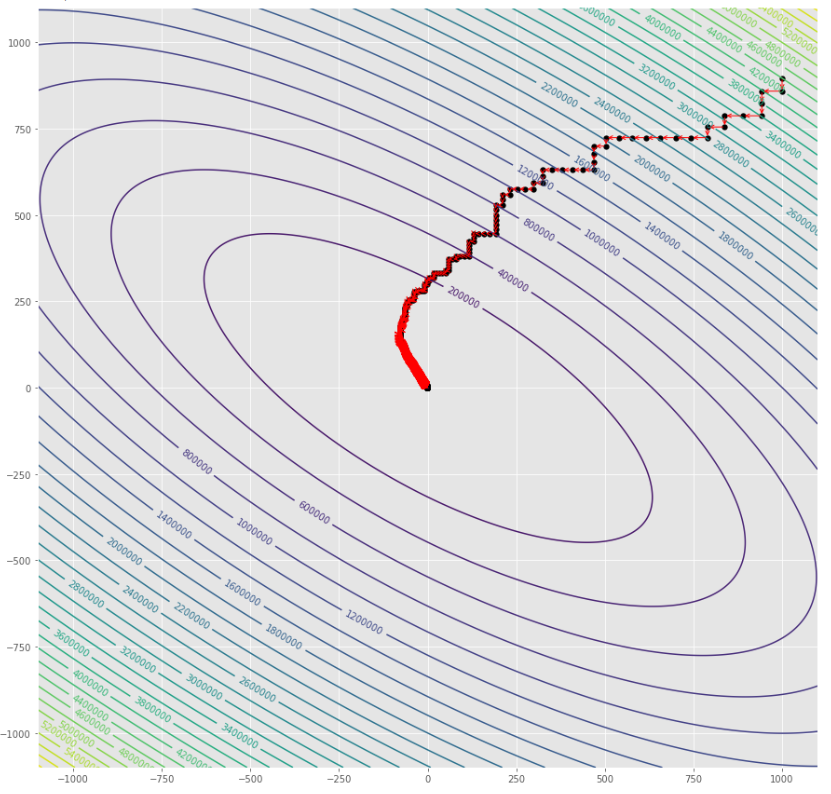
Trama de contorno 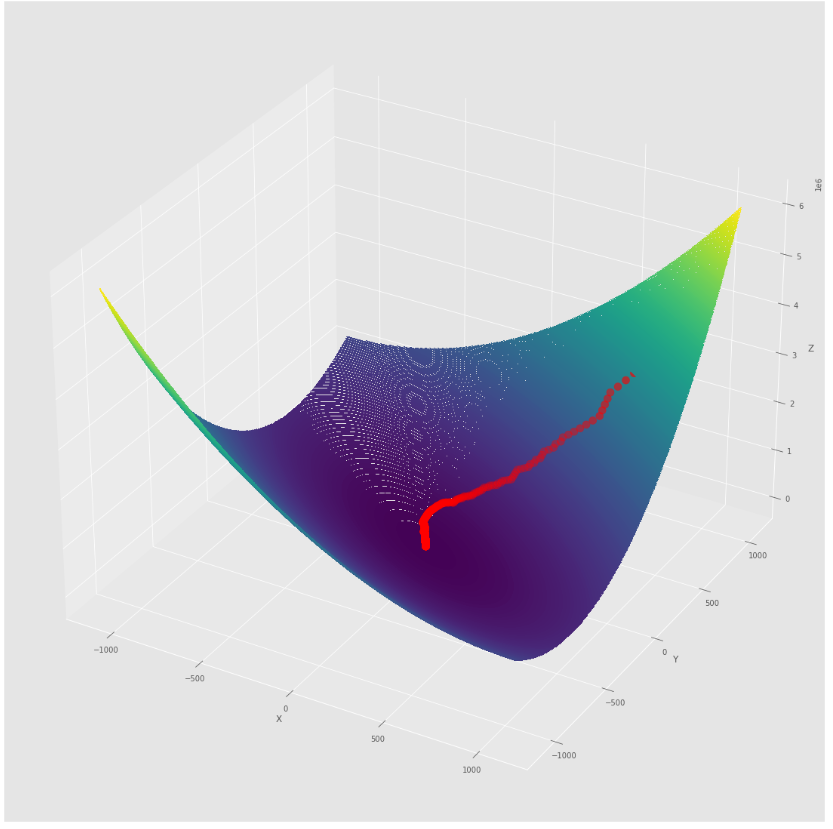
Trama 3D
alpha = 100 #it must be high because of BLS
c = 2
pmc . sgd_with_bls ( h , X , tol , alpha , c )
pm3 . sgd_with_bls ( h , X , tol , alpha , c ) Y* = [-1. 1.5] La secuencia de pasos dados por el descenso de gradiente estocástico con algoritmo BLS antes de alcanzar el mínimo 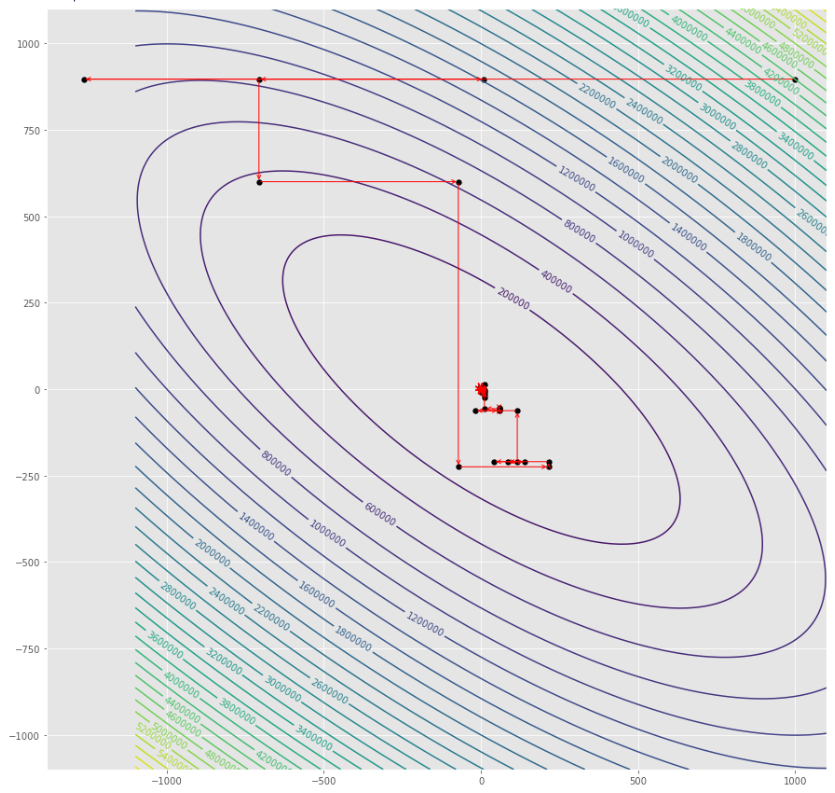
Trama de contorno 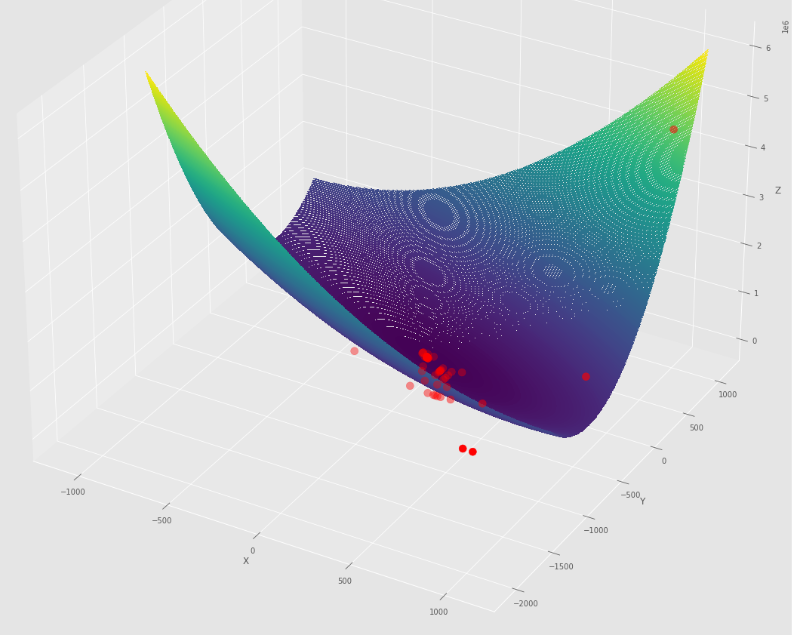
Trama 3D
pm3 . compare_all_time ( h , X , 1.e-2 , 1.e-1 , 100 , 2 ) Tiempo de ejecución 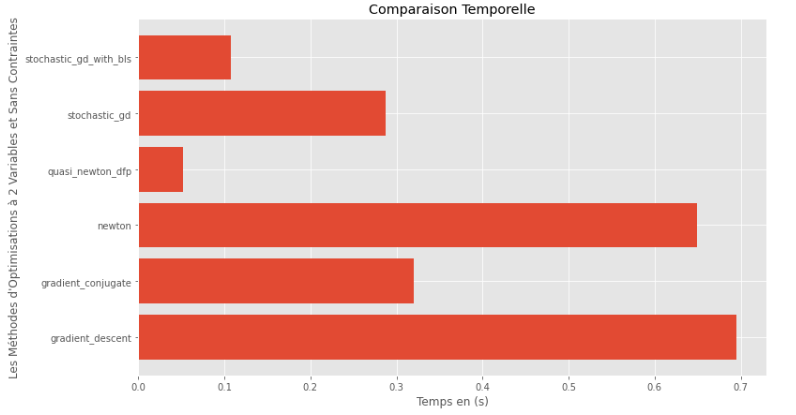
pm3 . compare_all_precision ( h , X , 1.e-2 , 1.e-1 , 100 , 2 ) Brecha entre mínimo verdadero y calculado 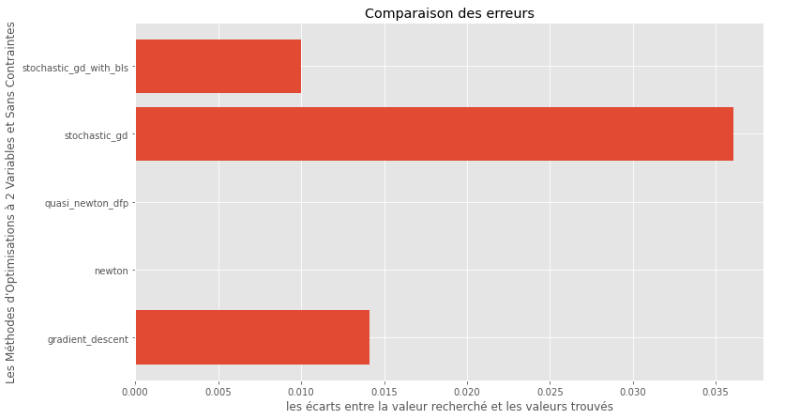
A partir del tiempo de ejecución y los gráficos de precisión, se puede deducir que entre los algoritmos evaluados para esta función multivariable convexa, el método cuasi Newton DFP surge como la opción óptima, ofreciendo una combinación de alta precisión y un tiempo de ejecución notablemente bajo.
import pyoptim . my_numpy . inverse as npi 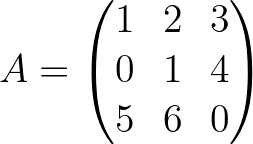
A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]]) A_1 = npi . gaussjordan ( A . copy ())
I = A @ A_1
I = np . around ( I , 1 )
print ( 'A_1 = n n ' , A_1 )
print ( ' n A_1*A = n n ' , I ) A_1 =
[[-24. 18. 5.]
[ 20. -15. -4.]
[ -5. 4. 1.]]
A_1*A =
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]] import pyoptim . my_numpy . decompose as npd A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]]) #A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ],[ - 1. , 2. , - 1. ],[ 0. , - 1. , 2. ]]) #B is positive definite
Y = np . array ([ 45 , - 78 , 95 ]) #randomly chosen column vector L , U , P = npd . LU ( A )
print ( "P = n " , P , " n n L = n " , L , " n n U = n " , U )
print ( " n " , A == P @ L @ U ) P =
[[0. 0. 1.]
[0. 1. 0.]
[1. 0. 0.]]
L =
[[1. 0. 0. ]
[0. 1. 0. ]
[0.2 0.8 1. ]]
U =
[[ 5. 6. 0. ]
[ 0. 1. 4. ]
[ 0. 0. -0.2]]
[[ True True True]
[ True True True]
[ True True True]] L = npd . choleski ( A ) # A is not positive definite
print ( L )
print ( "--------------------------------------------------" )
L = npd . choleski ( B ) # B is positive definite
print ( 'L = n ' , L , ' n ' )
C = np . around ( L @( L . T ), 1 )
print ( 'B = L@(L.T) n n ' , B == C ) A must be positive definite !
None
--------------------------------------------------
L =
[[ 1.41421356 0. 0. ]
[-0.70710678 1.22474487 0. ]
[ 0. -0.81649658 1.15470054]]
B = L@(L.T)
[[ True True True]
[ True True True]
[ True True True]] import pyoptim . my_numpy . solve as nps 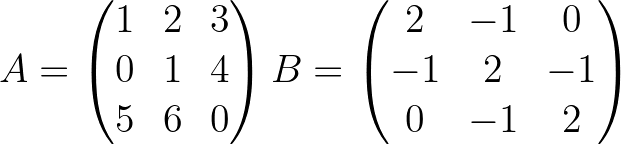
A = np . array ([[ 1. , 2. , 3. ], [ 0. , 1. , 4. ], [ 5. , 6. , 0. ]]) # A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ], [ - 1. , 2. , - 1. ], [ 0. , - 1. , 2. ]]) # B is positive definite
Y = np . array ([ 45 , - 78 , 95 ]) # randomly chosen column vector X = nps . gaussjordan ( A , Y )
print ( "X = n " , X )
print ( " n A@X=Y n " , A @ X == Y , ' n ' )
print ( '---------------------------------------------------------------' )
X = nps . gaussjordan ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n B@X=Y n " , Y_ == Y , ' n ' ) X =
[[-2009.]
[ 1690.]
[ -442.]]
A@X=Y
[[ True]
[ True]
[ True]]
---------------------------------------------------------------
X =
[[18.5]
[-8. ]
[43.5]]
B@X=Y
[[ True]
[ True]
[ True]]
X = nps . LU ( A , Y )
print ( "X* = n " , X )
print ( " n AX*=Y n " , A @ X == Y )
print ( "-------------------------------------------------------------------------------" );
X = nps . LU ( B , Y )
print ( "X* = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y ) X* =
[[-2009.]
[ 1690.]
[ -442.]]
AX*=Y
[[ True]
[ True]
[ True]]
-------------------------------------------------------------------------------
X* =
[[18.5]
[-8. ]
[43.5]]
BX*=Y
[[ True]
[ True]
[ True]] X = nps . choleski ( A , Y )
print ( "-------------------------------------------------------------------------------" )
X = nps . choleski ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y ) !! A must be positive definite !!
-------------------------------------------------------------------------------
X =
[[18.5]
[-8. ]
[43.5]]
BX*=Y
[[ True]
[ True]
[ True]]