скачать pyoptim - скачать исходный код pyoptim

Pyoptim: пакет Python для оптимизации и матрицы

Пакет Python, интегрирующий около десяти неограниченных алгоритмов оптимизации, включающих 2D/3D -визуализацию для сравнительного анализа и включенные операции матрицы.

Этот проект, компонент курса численного анализа и оптимизации в Ensias, Университет Мухаммеда V возник из предложения профессора М. Наума создать алгоритмы инкапсулирования Python, практикуемые во время лабораторных сессий. Он фокусируется примерно на десяти неограниченных алгоритмах оптимизации, предлагая 2D и 3D визуализации, что позволяет сравнить производительность в вычислительной эффективности и точности. Кроме того, проект охватывает матричные операции, такие как инверсия, разложение и решение линейных систем, все интегрированы в пакет, содержащий алгоритмы, полученные из лаборатории.

Источник GIF: https://www.nsf.gov/news/mmg/mmg_disp.jsp?med_id=78950&from==n(https://aria42.com/blog/2014/12/understanding-lbfgs

Каждая часть этого проекта - это пример кода, который показывает, как сделать следующее:

Реализация алгоритмов оптимизации с одной переменной, охватывающей фиксированную_step, accelerated_step, trushive_search, dichotomous_search, evternate_halling, fibonacci, Golden_section, armijo_backward и armijo_forward.
Включение различных алгоритмов оптимизации с одной переменной, в том числе градиент спуск, градиент, конъюгат, Ньютон, Quasi_newton_DFP, стохастический градиент.
Визуализация каждого шага итерации для всех алгоритмов в форматах 2D, контура и 3D.
Проведение сравнительного анализа, сосредоточенного на их показателях выполнения и точности.
Внедрение матричных операций, таких как инверсия (например, Гаусс-Джордан), разложение (например, Lu, Choleski) и решения для линейных систем (например, Гаусс-Джордан, Лу, Чолски).
Начиная

Чтобы установить этот пакет Python:

 pip install pyoptim

Запустите эту демонстрационную записную книжку

Документация и сравнительный анализ

Алгоритмы оптимизации единой переменной
- Импорт библиотек
- Функция объекта
- Инициализация параметра
- Фиксированный шаг
- Ускоренный шаг
- Исчерпывающий поиск
- Дихотомический поиск
- Интервал вдвое
- Фибоначчи
- Golden_Section
- Armijo_backward
- Armijo_forward
- Сравнительный анализ
Алгоритмы многомерных оптимизации
- Импорт библиотек
- Функция объекта
- Инициализация параметра
- Градиент спуск
- Градиент конъюгат
- Ньютон
- Quasi Newton DFP
- Стохастический градиент спуск
- Стохастический градиент спуск с BLS
- Сравнительный анализ
Матрица обратная
- Импорт библиотек
- Тестовая матрица
- Гаусс Джордан
- Матрица обратная
- Матрица обратная
Матричная разложение
- Импорт библиотек
- Тестовая матрица
- Лу
- Чолески
Решение линейной системы
- Импорт библиотек
- Тестовая матрица
- Гаусс Джордан
- Лу
- Чолески

Алгоритмы оптимизации единой переменной

Импорт библиотек

 import pyoptim . my_scipy . onevar_optimize . minimize as soom
import pyoptim . my_plot . onevar . _2D as po2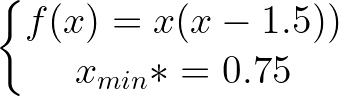

Функция объекта

 def f ( x ):
    return x * ( x - 1.5 )   # analytically, argmin(f) = 0.75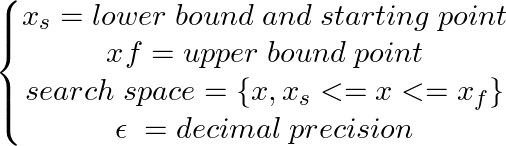

Инициализация параметра

 xs = - 10
xf = 10
epsilon = 1.e-2

Фиксированный шаг

 print ( 'x* =' , soom . fixed_step ( f , xs , epsilon ))
po2 . fixed_step ( f , xs , epsilon )

 x* = 0.75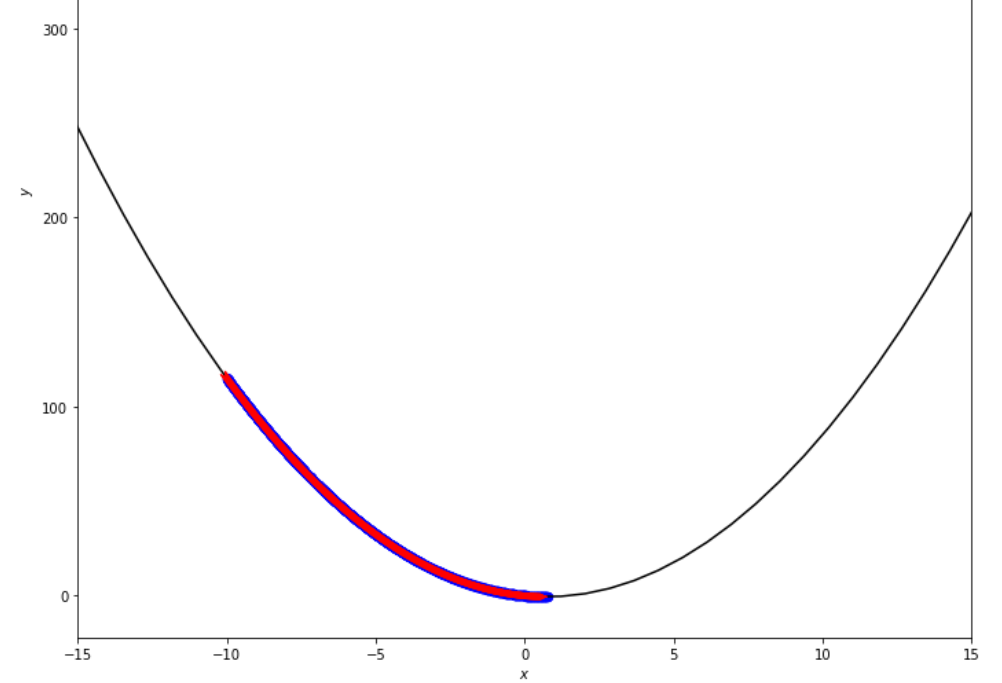

Последовательность шагов, предпринятых с помощью алгоритма фиксированного шага, прежде чем достичь минимального

Ускоренный шаг

 print ( 'x* =' , soom . accelerated_step ( f , xs , epsilon ))
po2 . accelerated_step ( f , xs , epsilon )

 x* = 0.86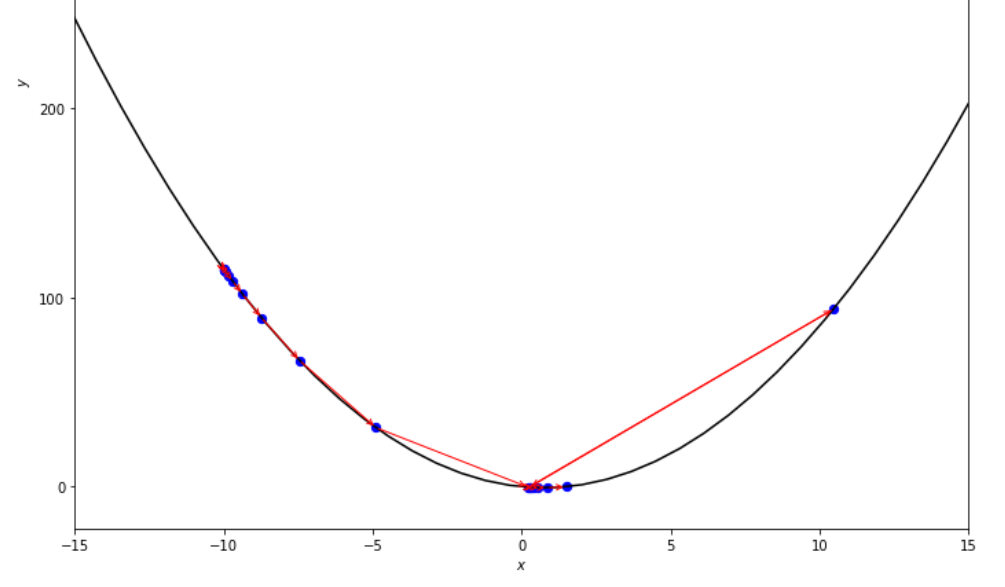

Последовательность шагов, предпринятых с помощью ускоренного алгоритма шага до достижения минимального

Исчерпывающий поиск

 print ( 'x* =' , soom . exhaustive_search ( f , xs , xf , epsilon ))
po2 . exhaustive_search ( f , xs , xf , epsilon )

 x* = 0.75

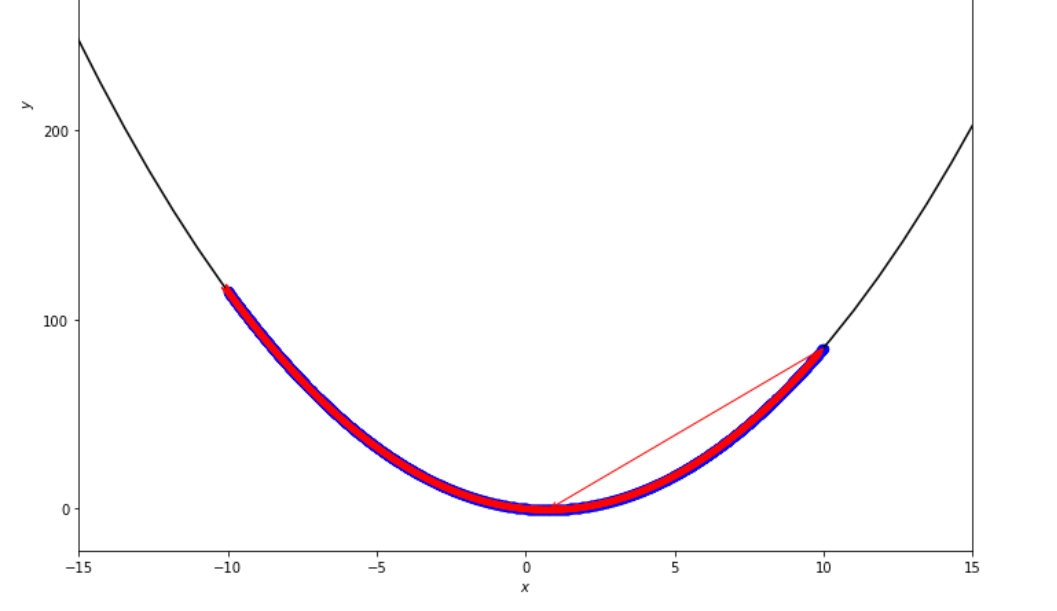
Последовательность шагов, предпринятых с помощью исчерпывающего алгоритма поиска, прежде чем достичь минимального

Дихотомический поиск

 mini_delta = 1.e-3
print ( 'x* =' , soom . dichotomous_search ( f , xs , xf , epsilon , mini_delta ))
po2 . dichotomous_search ( f , xs , xf , epsilon , mini_delta )

 x* = 0.7494742431640624

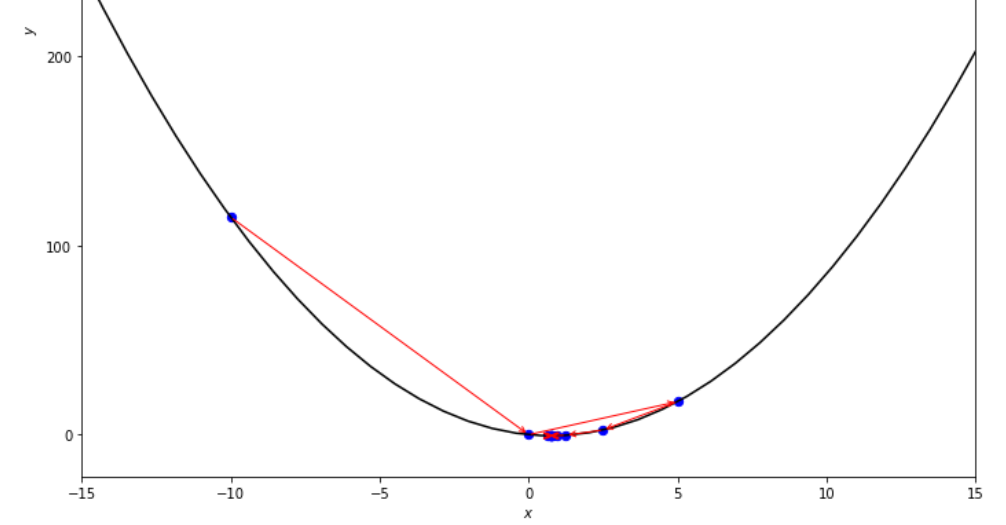
Последовательность шагов, предпринятых дихотомическим алгоритмом поиска, прежде чем достичь минимума

Интервал вдвое

 print ( 'x* =' , soom . interval_halving ( f , xs , xf , epsilon ))
po2 . interval_halving ( f , xs , xf , epsilon )

 x* = 0.75

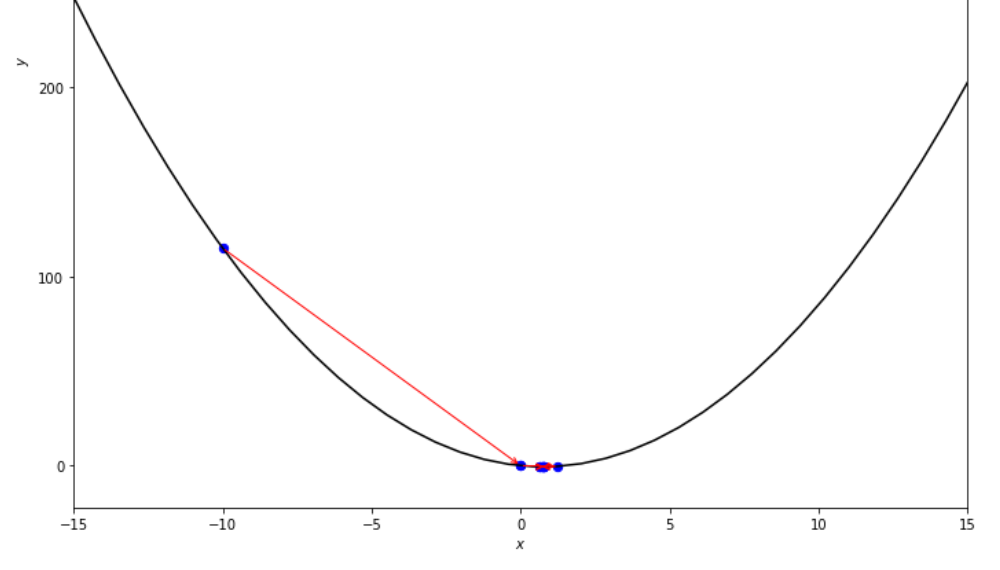
Последовательность шагов, предпринятых с помощью алгоритма с интервалом вдвое, до достижения минимума.

Фибоначчи

 n = 15
print ( 'x* =' , soom . fibonacci ( f , xs , xf , n )) 
po2 . fibonacci ( f , xs , xf , n )

 x* = 0.76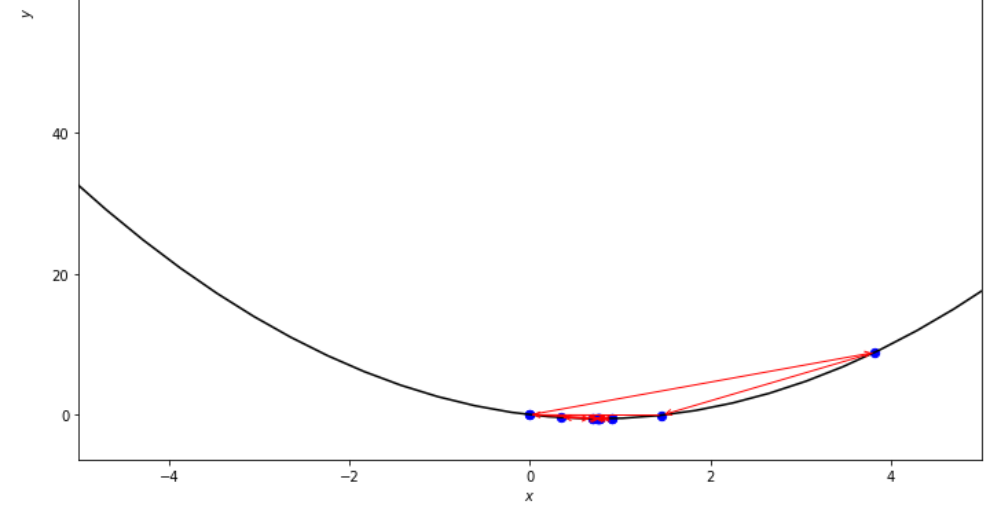

Последовательность шагов, предпринятых алгоритмом Фибоначчи, до достижения минимума.

Золотая секция

 print ( 'x* =' , soom . golden_section ( f , xs , xf , epsilon ))
po2 . golden_section ( f , xs , xf , epsilon )

 x* = 0.75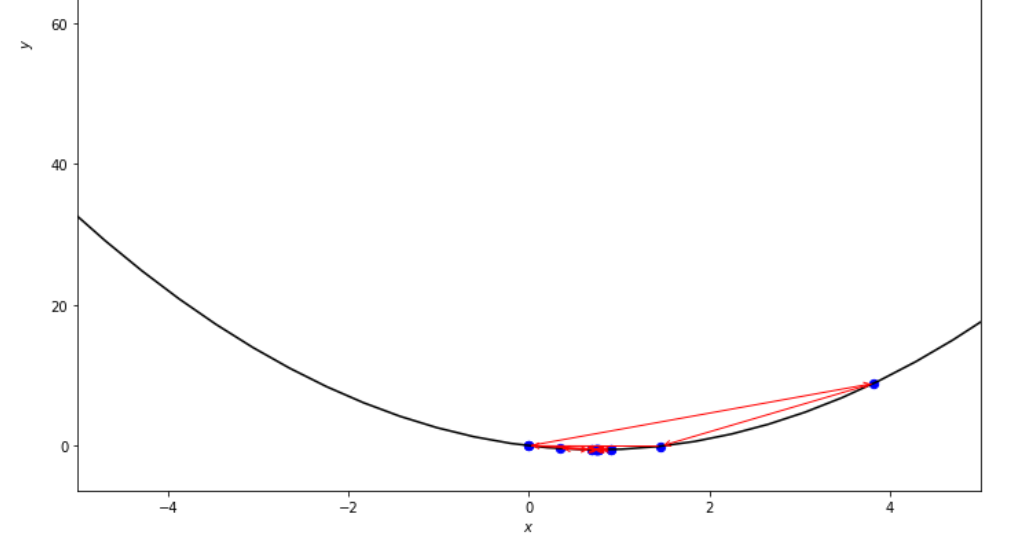

Последовательность шагов, предпринятых алгоритмом золотой секции, прежде чем достичь минимального

Армихо назад

 ŋ = 2
xs = 100
print ( 'x* =' , soom . armijo_backward ( f , xs , ŋ , epsilon ))
po2 . armijo_backward ( f , xs , ŋ , epsilon )

 x* = 0.78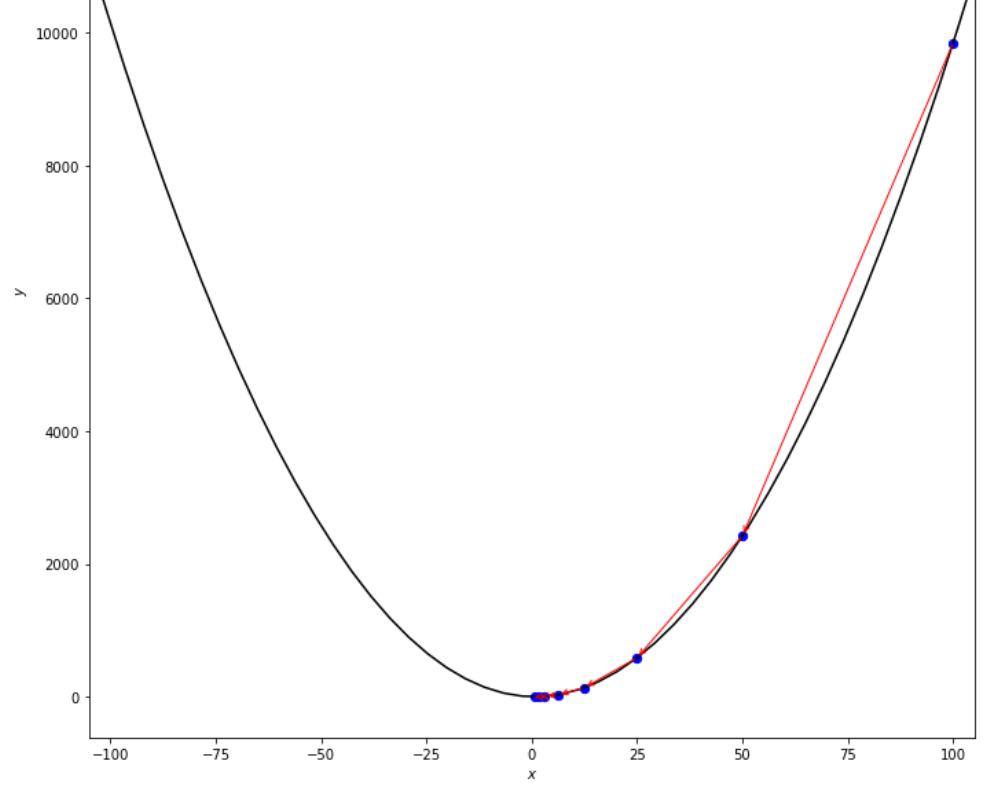

Последовательность шагов, сделанных алгоритмом Armijo, до достижения минимума

Армихо вперед

 xs = 0.1
epsilon = 0.5
ŋ = 2
print ( 'x* =' , soom . armijo_forward ( f , xs , ŋ , epsilon ))
po2 . armijo_forward ( f , xs , ŋ , epsilon )

 x* = 0.8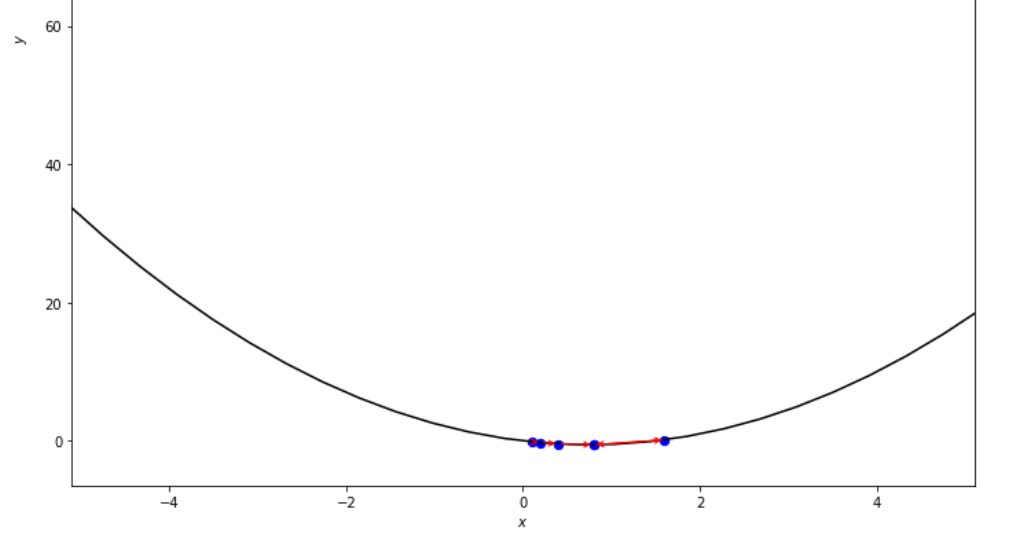

Последовательность шагов, предпринятых алгоритмом прямого Армихо, до достижения минимального

Сравнительный анализ

 po2 . compare_all_time ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 )

Время выполнения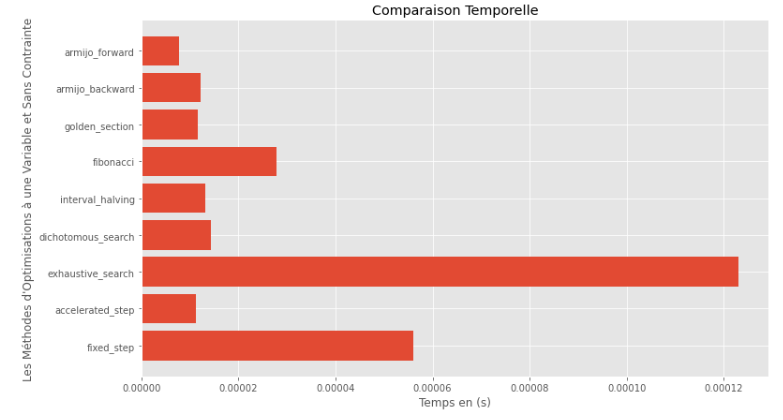

 po2 . compare_all_precision ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 )

Разрыв между истинным и вычисленным минимальным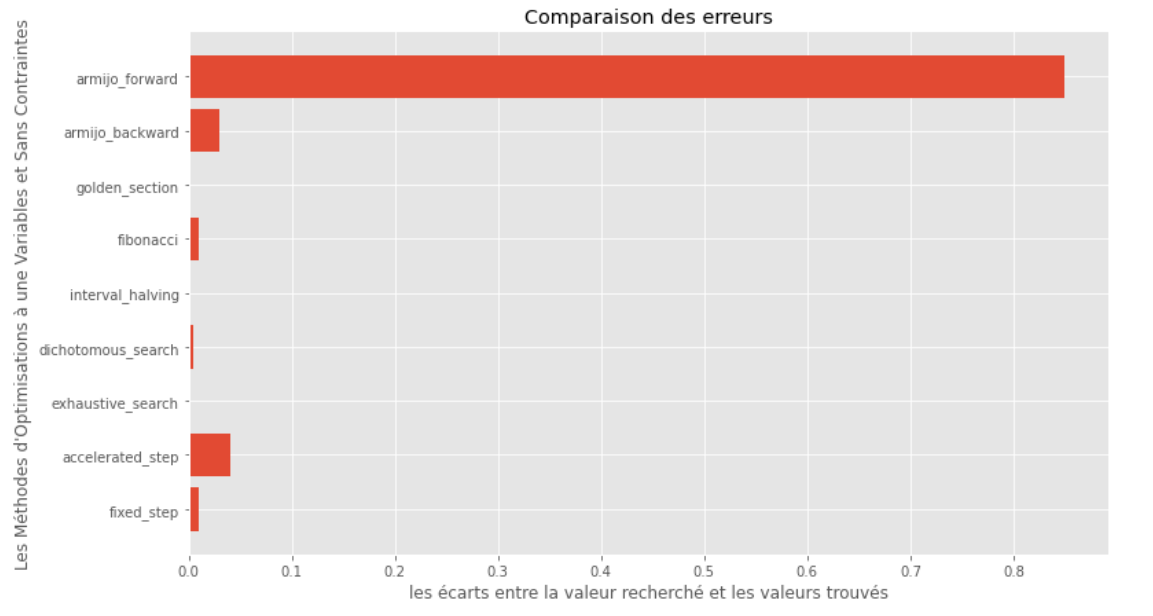

Из графиков времени выполнения и точности можно сделать вывод, что среди алгоритмов, оцениваемых для этой выпуктной функции с одной переменной, метод золотого секции появляется как оптимальный выбор, предлагая смесь высокой точности и особенно низкой времени выполнения.

Алгоритмы многомерных оптимизации

Импорт библиотек

 import pyoptim . my_plot . multivar . _3D as pm3
import pyoptim . my_plot . multivar . contour2D as pmc

Функция объекта

 def h ( x ):
    return x [ 0 ] - x [ 1 ] + 2 * ( x [ 0 ] ** 2 ) + 2 * x [ 1 ] * x [ 0 ] + x [ 1 ] ** 2
# analytically, argmin(f) = [-1, 1.5]

Аналичное решение

Инициализация параметра

 X = [ 1000 , 897 ]
alpha = 1.e-2
tol = 1.e-2

Градиент спуск

 pmc . gradient_descent ( h , X , tol , alpha )
pm3 . gradient_descent ( h , X , tol , alpha )

 Y* =  [-1.01  1.51]

Последовательность шагов, предпринятых алгоритмом градиентного спуска, прежде чем достичь минимального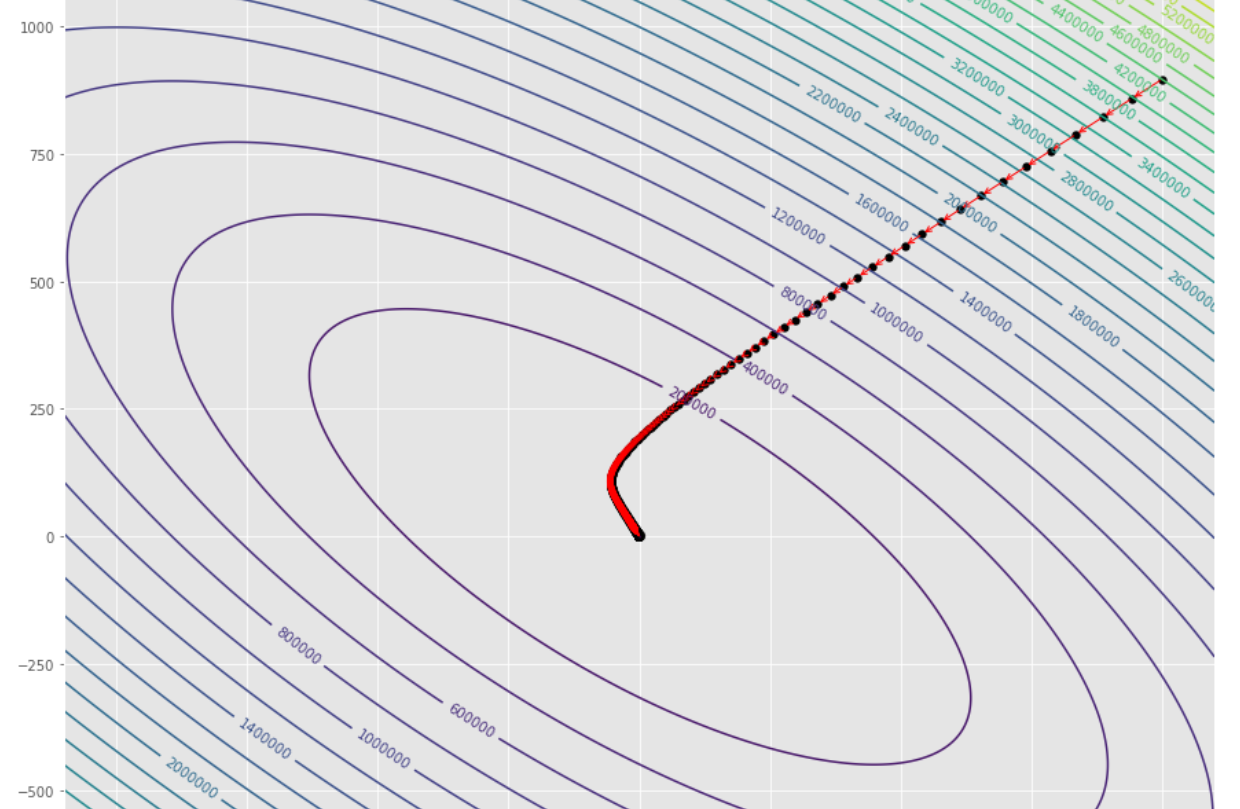

Контурный сюжет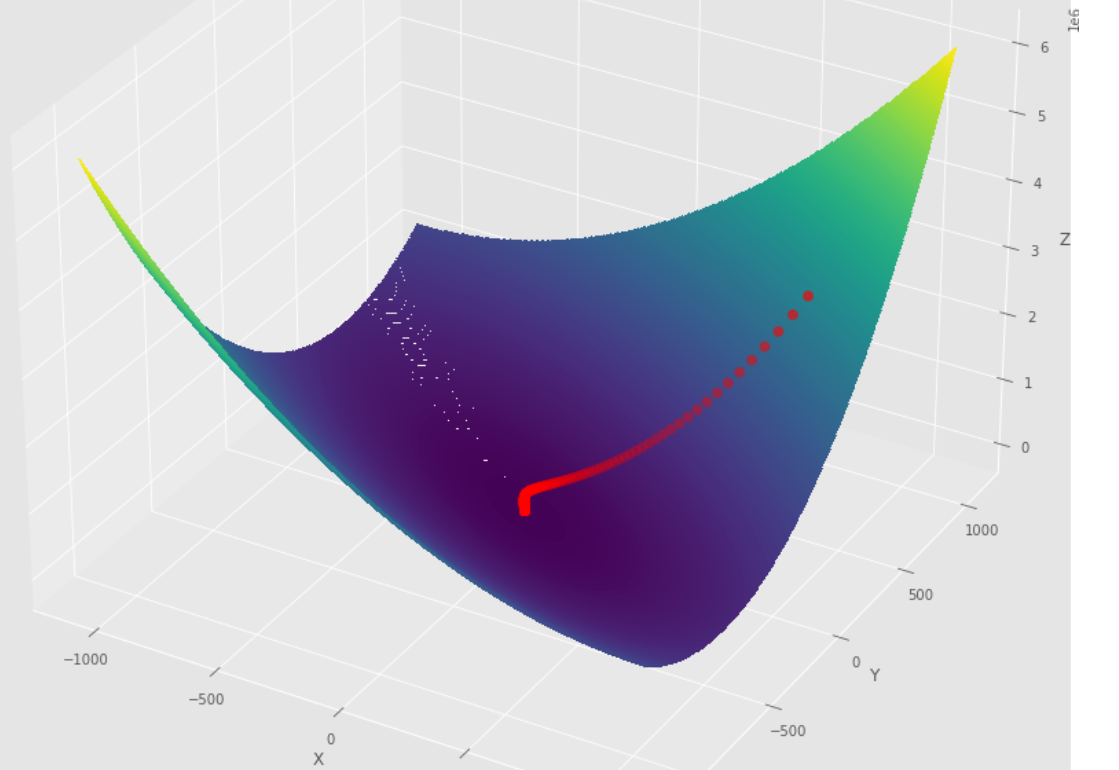

3 -й сюжет

Градиент конъюгат

 pmc . gradient_conjugate ( h , X , tol )
pm3 . gradient_conjugate ( h , X , tol )

 Y* =  [-107.38  172.18]

Последовательность шагов, предпринятых с помощью алгоритма градиентного конъюгата до достижения минимального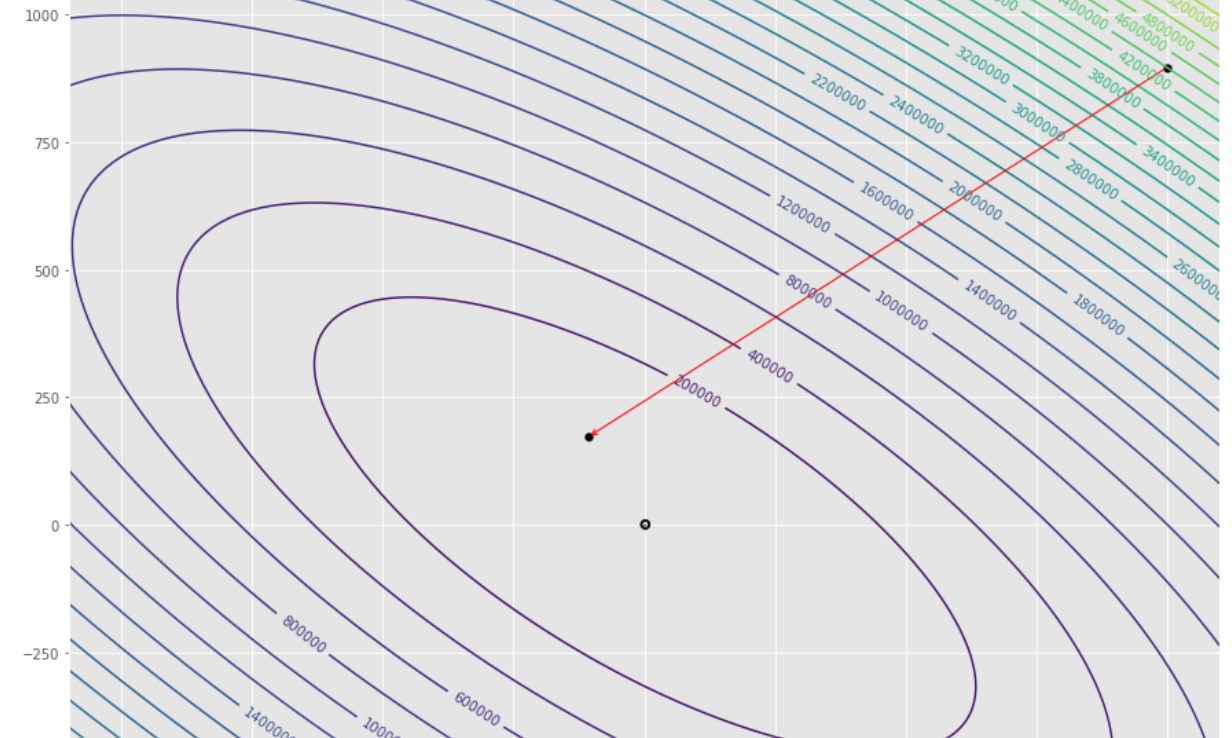

Контурный сюжет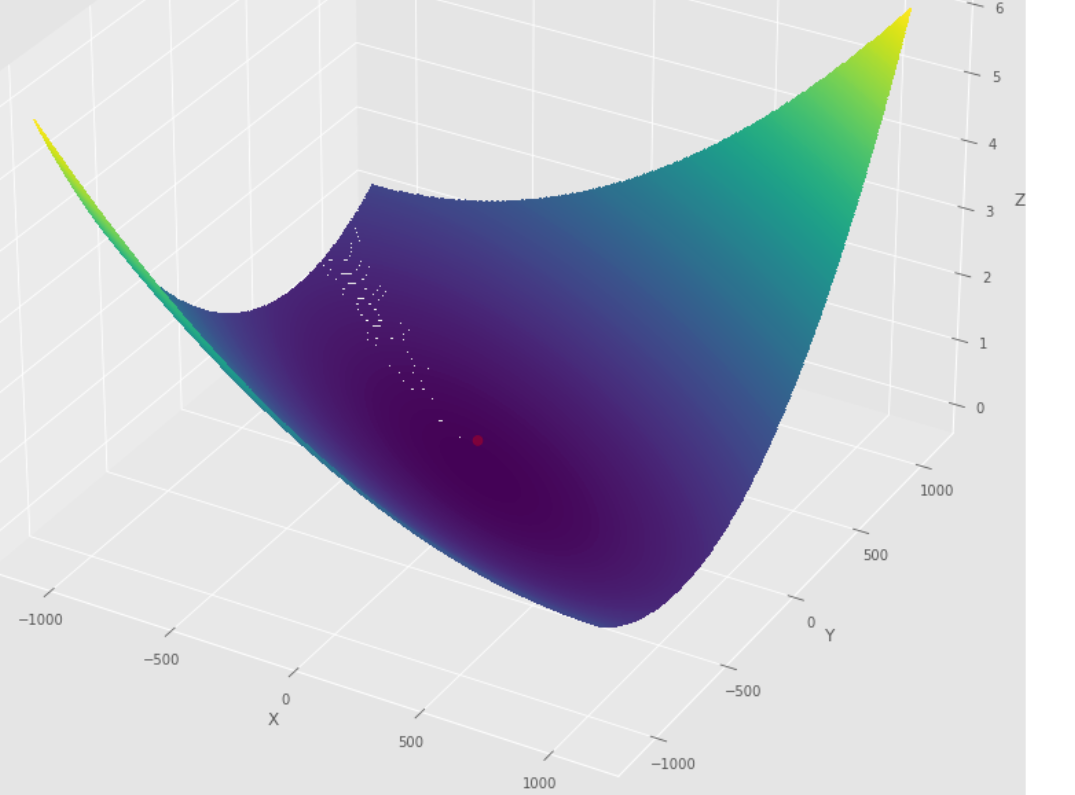

3 -й сюжет

Ньютон

 pmc . newton ( h , X , tol )
pm3 . newton ( h , X , tol )

 Y* =  [-1.   1.5]

Последовательность шагов, предпринятых алгоритмом Ньютона, до достижения минимального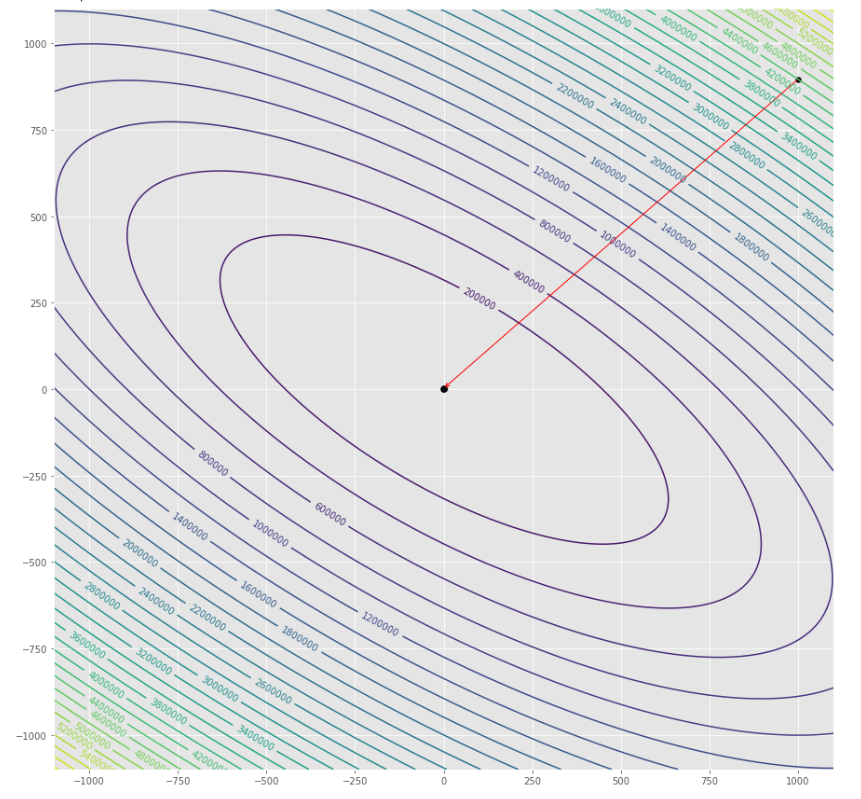

Контурный сюжет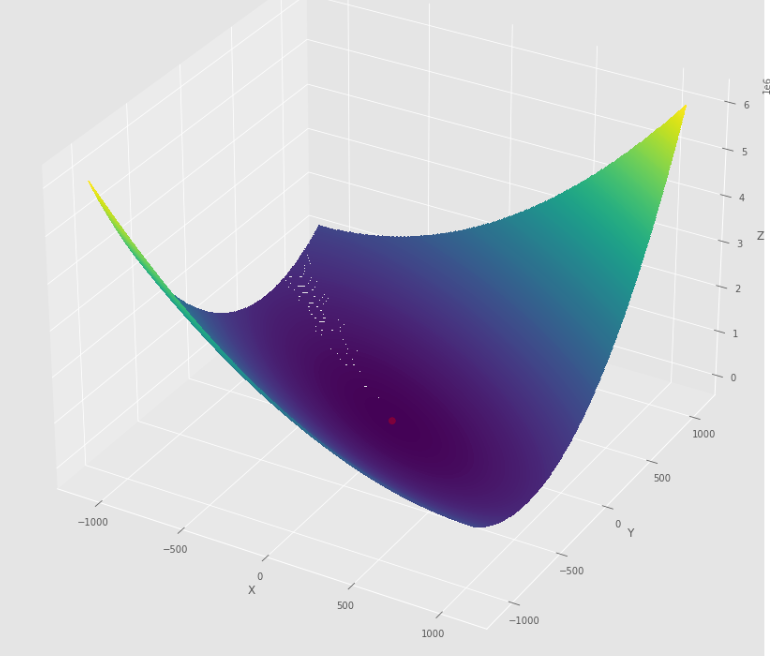

3 -й сюжет

Quasi Newton DFP

 pmc . quasi_newton_dfp ( h , X , tol )
pm3 . quasi_newton_dfp ( h , X , tol )

 Y* =  [-1.   1.5]

Последовательность шагов, предпринятых алгоритмом квази Ньютона DFP, до достижения минимума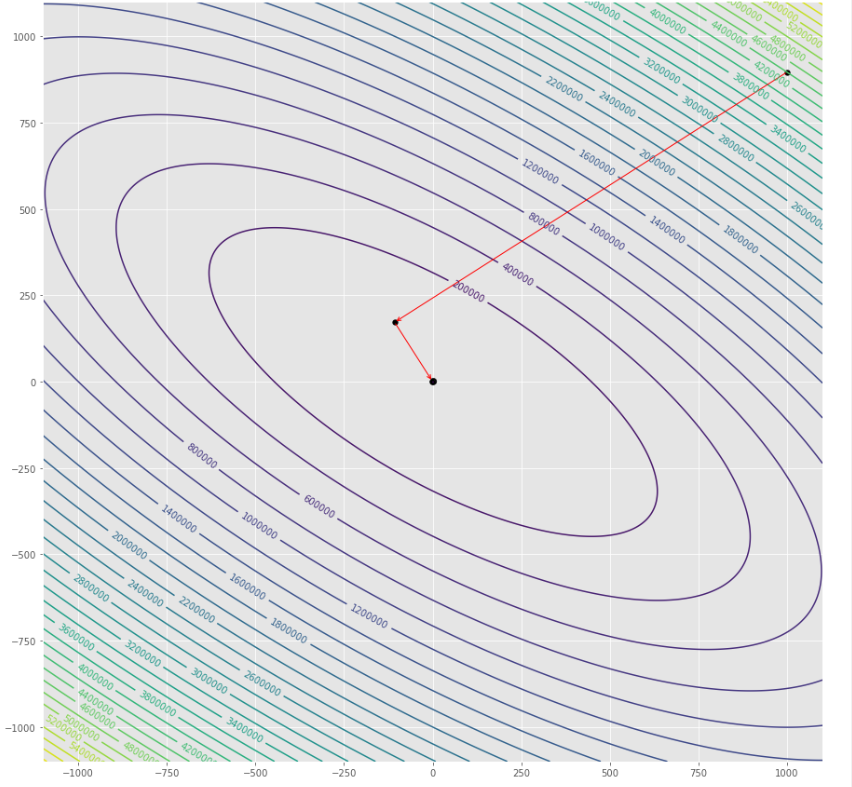

Контурный сюжет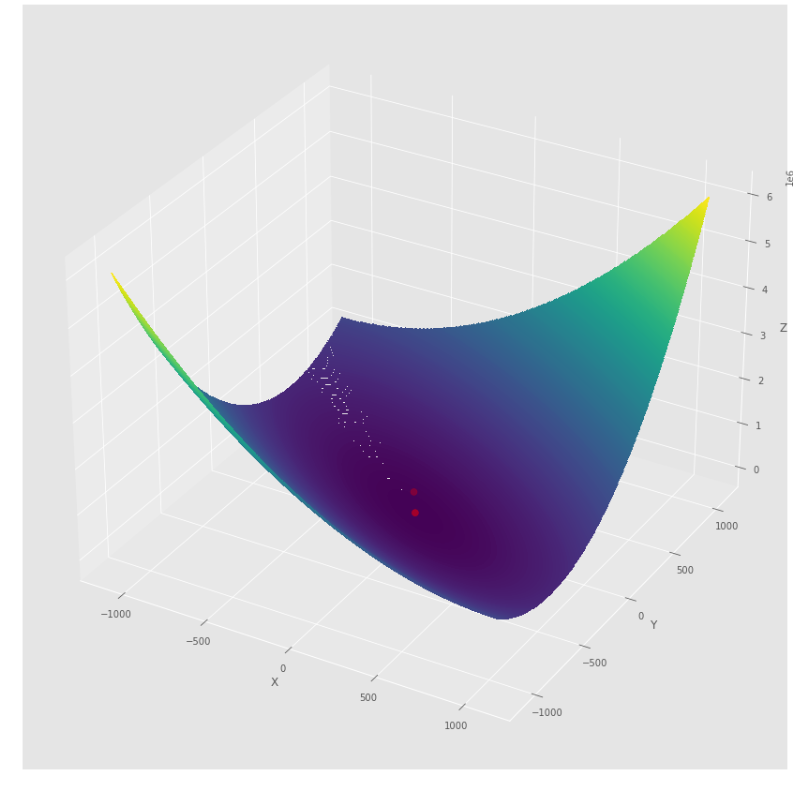

3 -й сюжет

Стохастический градиент спуск

 pmc . sgd ( h , X , tol , alpha )
pm3 . sgd ( h , X , tol , alpha )

 Y* =  [-1.01  1.52]

Последовательность шагов, предпринятых алгоритмом спуска стохастического градиента, прежде чем достичь минимума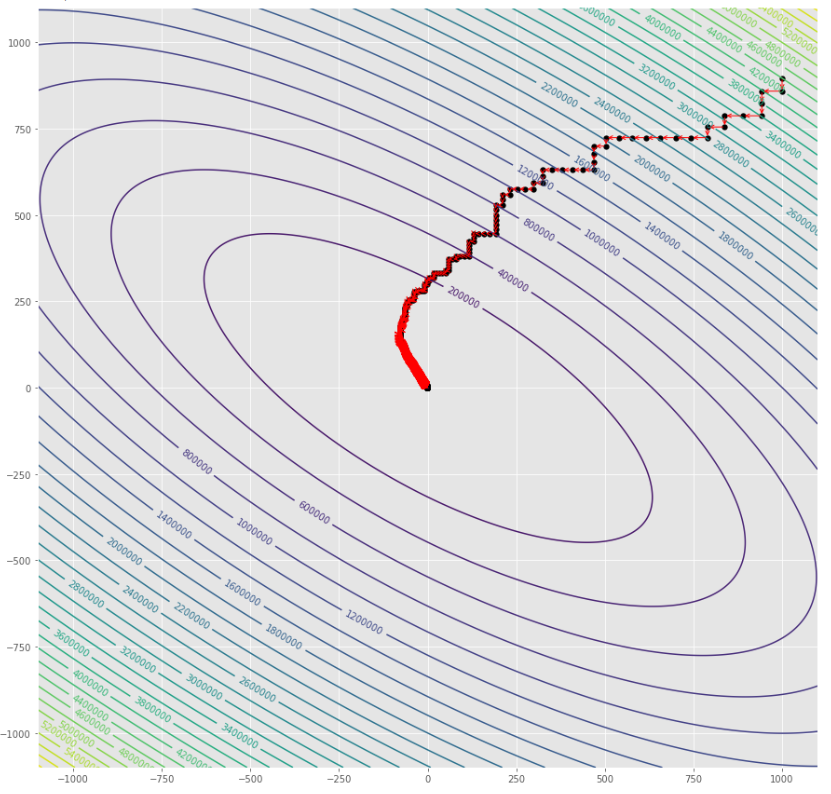

Контурный сюжет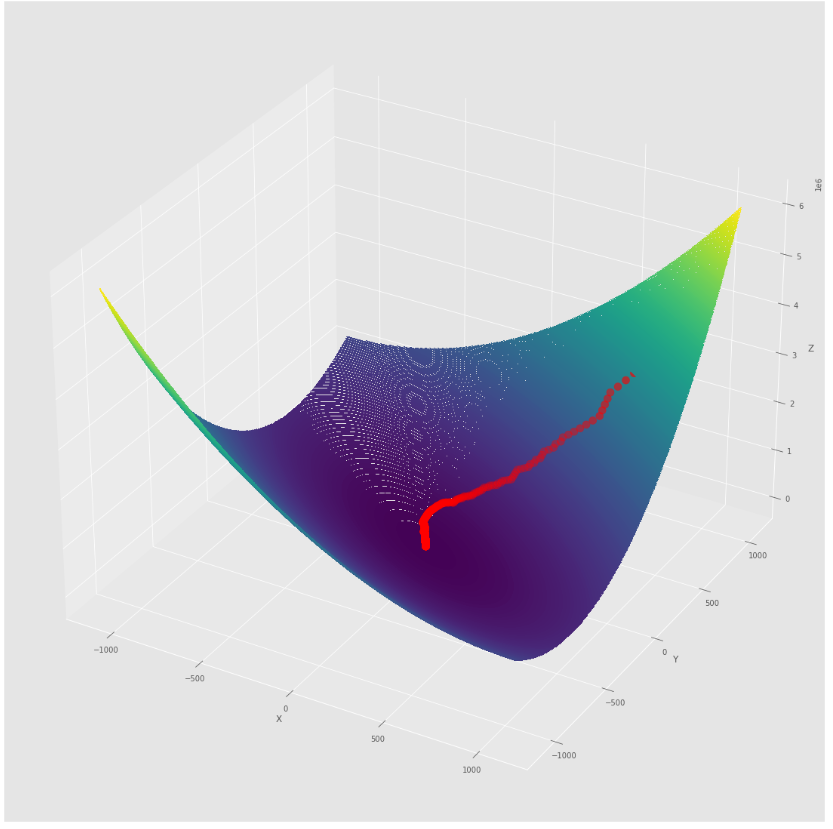

3 -й сюжет

Стохастический градиент спуск с BLS

 alpha = 100 #it must be high because of BLS
c = 2
pmc . sgd_with_bls ( h , X , tol , alpha , c ) 
pm3 . sgd_with_bls ( h , X , tol , alpha , c )

 Y* =  [-1.   1.5]

Последовательность шагов, предпринятых с помощью стохастического градиента с алгоритмом BLS, прежде чем достичь минимального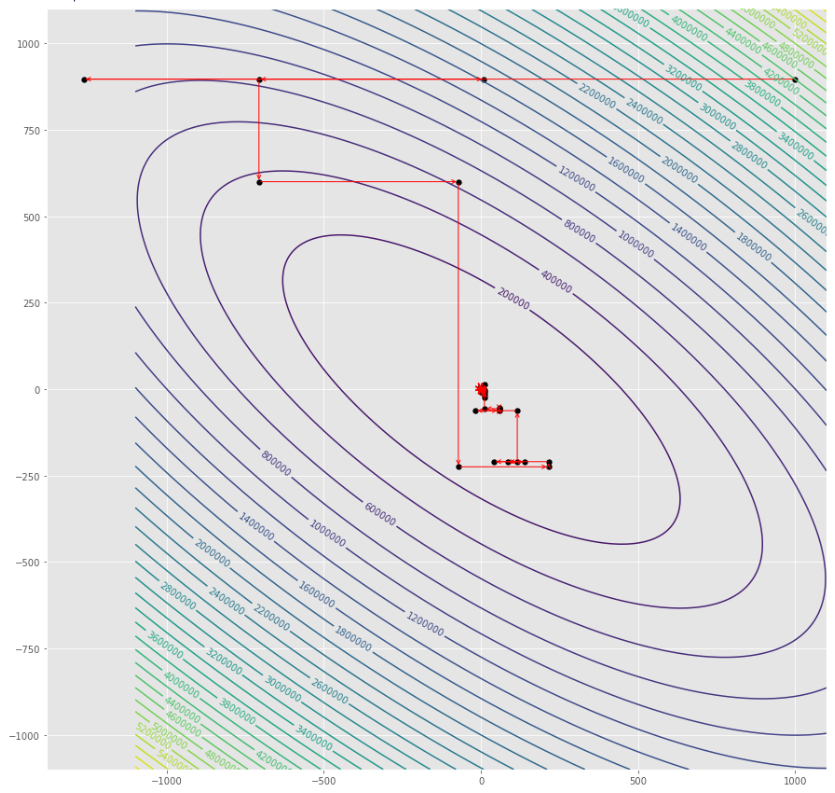

Контурный сюжет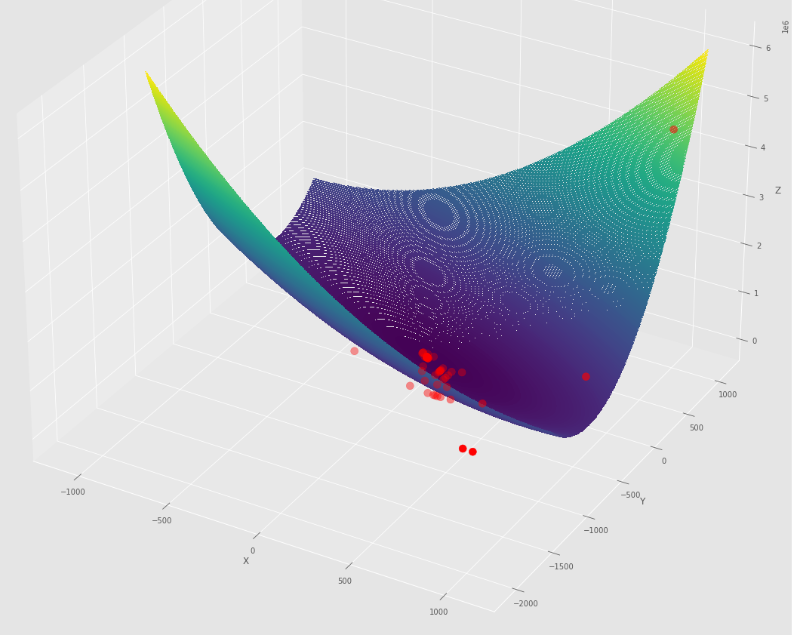

3 -й сюжет

Сравнительный анализ

 pm3 . compare_all_time ( h , X , 1.e-2 , 1.e-1 , 100 , 2 )

Время выполнения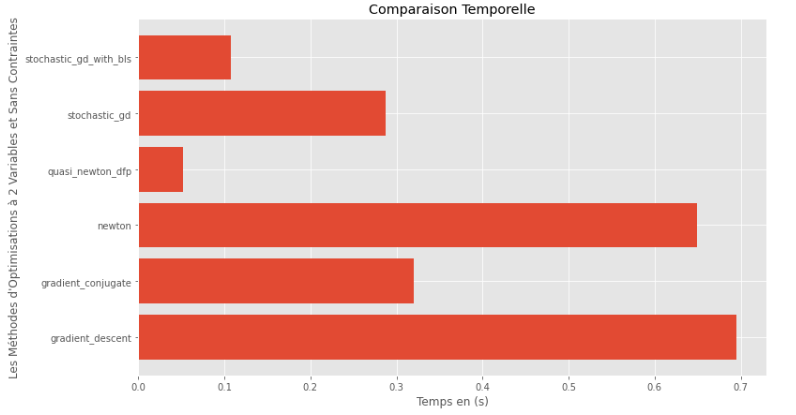

 pm3 . compare_all_precision ( h , X , 1.e-2 , 1.e-1 , 100 , 2 )

Разрыв между истинным и вычисленным минимальным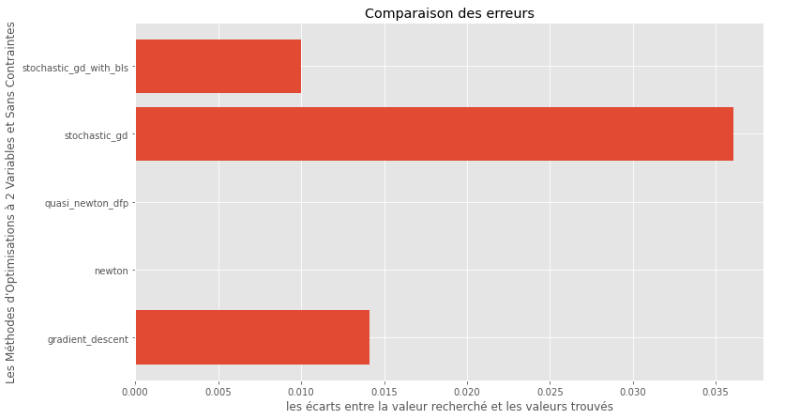

Из графиков времени выполнения и точности можно сделать вывод, что среди алгоритмов, оцениваемых для этой выпуклой многофункциональной функции, метод Quasi Newton DFP появляется в качестве оптимального выбора, предлагая смесь высокой точности и, в частности, низкой времени выполнения.

Матрица обратная

Импортировать библиотеки

 import pyoptim . my_numpy . inverse as npi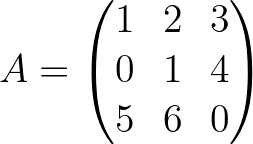

Тестовая матрица

 A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]])

Гаусс Джордан

 A_1 = npi . gaussjordan ( A . copy ())
I = A @ A_1
I = np . around ( I , 1 )
print ( 'A_1 = n n ' , A_1 )
print ( ' n A_1*A = n n ' , I )

 A_1 =

 [[-24.  18.   5.]
 [ 20. -15.  -4.]
 [ -5.   4.   1.]]

A_1*A =

 [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

Матричная разложение

Импорт

 import pyoptim . my_numpy . decompose as npd

Тестовая матрица

 A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]])      #A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ],[ - 1. , 2. , - 1. ],[ 0. , - 1. , 2. ]])  #B is positive definite
Y = np . array ([ 45 , - 78 , 95 ])                               #randomly chosen column vector

Лу

 L , U , P = npd . LU ( A )
print ( "P = n " , P , " n n L = n " , L , " n n U = n " , U )
print ( " n " , A == P @ L @ U )

 P =
 [[0. 0. 1.]
 [0. 1. 0.]
 [1. 0. 0.]] 

L =
 [[1.  0.  0. ]
 [0.  1.  0. ]
 [0.2 0.8 1. ]] 

U =
 [[ 5.   6.   0. ]
 [ 0.   1.   4. ]
 [ 0.   0.  -0.2]]

 [[ True  True  True]
 [ True  True  True]
 [ True  True  True]]

Чолески

 L = npd . choleski ( A )          # A is not positive definite
print ( L )
print ( "--------------------------------------------------" )
L = npd . choleski ( B )          # B is positive definite 
print ( 'L = n ' , L , ' n ' )

C = np . around ( L @( L . T ), 1 )
print ( 'B = L@(L.T) n n ' , B == C )

 A must be positive definite !
None
--------------------------------------------------
L =
 [[ 1.41421356  0.          0.        ]
 [-0.70710678  1.22474487  0.        ]
 [ 0.         -0.81649658  1.15470054]] 

B = L@(L.T) 

 [[ True  True  True]
 [ True  True  True]
 [ True  True  True]]

Решение линейных систем

Импорт

 import pyoptim . my_numpy . solve as nps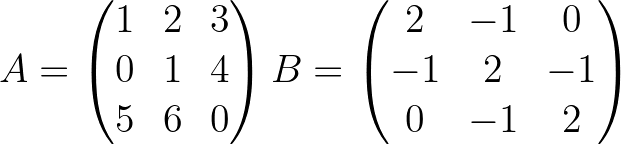

Тестовая матрица

 A = np . array ([[ 1. , 2. , 3. ], [ 0. , 1. , 4. ], [ 5. , 6. , 0. ]]) # A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ], [ - 1. , 2. , - 1. ], [ 0. , - 1. , 2. ]]) # B is positive definite
Y = np . array ([ 45 , - 78 , 95 ]) # randomly chosen column vector

Гаусс Джордан

 X = nps . gaussjordan ( A , Y )
print ( "X = n " , X )
print ( " n A@X=Y n " , A @ X == Y , ' n ' )

print ( '---------------------------------------------------------------' )
X = nps . gaussjordan ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n B@X=Y n " , Y_ == Y , ' n ' )

 X =
 [[-2009.]
 [ 1690.]
 [ -442.]]

 A@X=Y 
 [[ True]
 [ True]
 [ True]] 

---------------------------------------------------------------
X =
 [[18.5]
 [-8. ]
 [43.5]]

 B@X=Y 
 [[ True]
 [ True]
 [ True]]

Лу

 X = nps . LU ( A , Y )
print ( "X* = n " , X )
print ( " n AX*=Y n " , A @ X == Y )
print ( "-------------------------------------------------------------------------------" );
X = nps . LU ( B , Y )
print ( "X* = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y )

 X* =
 [[-2009.]
 [ 1690.]
 [ -442.]]

AX*=Y 
 [[ True]
 [ True]
 [ True]]
-------------------------------------------------------------------------------
X* =
 [[18.5]
 [-8. ]
 [43.5]]

BX*=Y
 [[ True]
 [ True]
 [ True]]

Чолески

 X = nps . choleski ( A , Y )
print ( "-------------------------------------------------------------------------------" )
X = nps . choleski ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y )

 !! A must be positive definite !!
-------------------------------------------------------------------------------
X =
 [[18.5]
 [-8. ]
 [43.5]]

BX*=Y
 [[ True]
 [ True]
 [ True]]

Расширять