Download de pyoptim - Download de código fonte de pyoptim

Pyoptim: pacote Python para operações de otimização e matriz

Um pacote Python que integra cerca de dez algoritmos de otimização sem restrições, incluindo visualizações 2D/3D para análise comparativa e operações de matriz incorporadas.

Este projeto, um componente do curso de análise e otimização numérica em Ensias, Mohammed V University, surgiu da sugestão do professor M. Naoum de criar um pacote Python que encapsulou algoritmos praticados durante as sessões de laboratório. Ele se concentra em cerca de dez algoritmos de otimização sem restrições, oferecendo visualizações 2D e 3D, permitindo uma comparação de desempenho na eficiência e precisão computacional. Além disso, o projeto abrange operações de matriz, como inversão, decomposição e resolução de sistemas lineares, todos integrados no pacote que contém os algoritmos derivados do laboratório.

Fonte do GIF: https://www.nsf.gov/news/mmg/mmg_disp.jsp?med_id=78950&from= ](https://aria42.com/blog/2014/12/undestanding-lbfgs

Cada parte deste projeto é o código de exemplo, que mostra como fazer o seguinte:

Implementação de algoritmos de otimização de uma variável, abrangendo fixo_step, acelerado_step, exaustivo_search, dichotomous_search, interval_halving, fibonacci, Golden_section, armijo_backward e Armijo_forward.
Incorporação de vários algoritmos de otimização unidiriável, incluindo descida de gradiente, conjugado de gradiente, newton, quase_newton_dfp, descida de gradiente estocástico.
Visualização de cada etapa de iteração para todos os algoritmos nos formatos 2D, contorno e 3D.
Conduzindo uma análise comparativa com foco em suas métricas de tempo de execução e precisão.
Implementação de operações de matriz, como inversão (por exemplo, gauss-jordan), decomposição (por exemplo, lu, choleski) e soluções para sistemas lineares (por exemplo, Gauss-Jordan, Lu, Choleski).
Começando

Para instalar este pacote Python:

 pip install pyoptim

Execute este caderno de demonstração

Documentação e análise comparativa

Índice

Algoritmos de otimização de variável única
- Importação de bibliotecas
- Função objectif
- Inicialização do parâmetro
- Etapa fixa
- Etapa acelerada
- Pesquisa exaustiva
- Pesquisa dicotômica
- Intervalo pela metade da metade
- Fibonacci
- Golden_Section
- Armijo_backward
- Armijo_forward
- Análise comparativa
Algoritmos de otimização multivariável
- Importação de bibliotecas
- Função objectif
- Inicialização do parâmetro
- Descendência de gradiente
- Conjugado de gradiente
- Newton
- Quasi Newton DFP
- Descendência de gradiente estocástico
- Descendência de gradiente estocástica com BLS
- Análise comparativa
Matriz inversa
- Importação de bibliotecas
- Matriz de teste
- Gauss Jordan
- Matriz inversa
- Matriz inversa
Decomposição da matriz
- Importação de bibliotecas
- Matriz de teste
- Lu
- Choleski
Resolvendo o sistema linear
- Importação de bibliotecas
- Matriz de teste
- Gauss Jordan
- Lu
- Choleski

Algoritmos de otimização de variável única

Importação de bibliotecas

 import pyoptim . my_scipy . onevar_optimize . minimize as soom
import pyoptim . my_plot . onevar . _2D as po2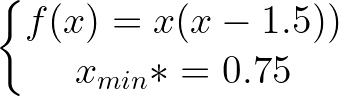

Função objectif

 def f ( x ):
    return x * ( x - 1.5 )   # analytically, argmin(f) = 0.75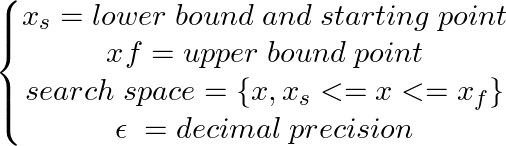

Inicialização do parâmetro

 xs = - 10
xf = 10
epsilon = 1.e-2

Etapa fixa

 print ( 'x* =' , soom . fixed_step ( f , xs , epsilon ))
po2 . fixed_step ( f , xs , epsilon )

 x* = 0.75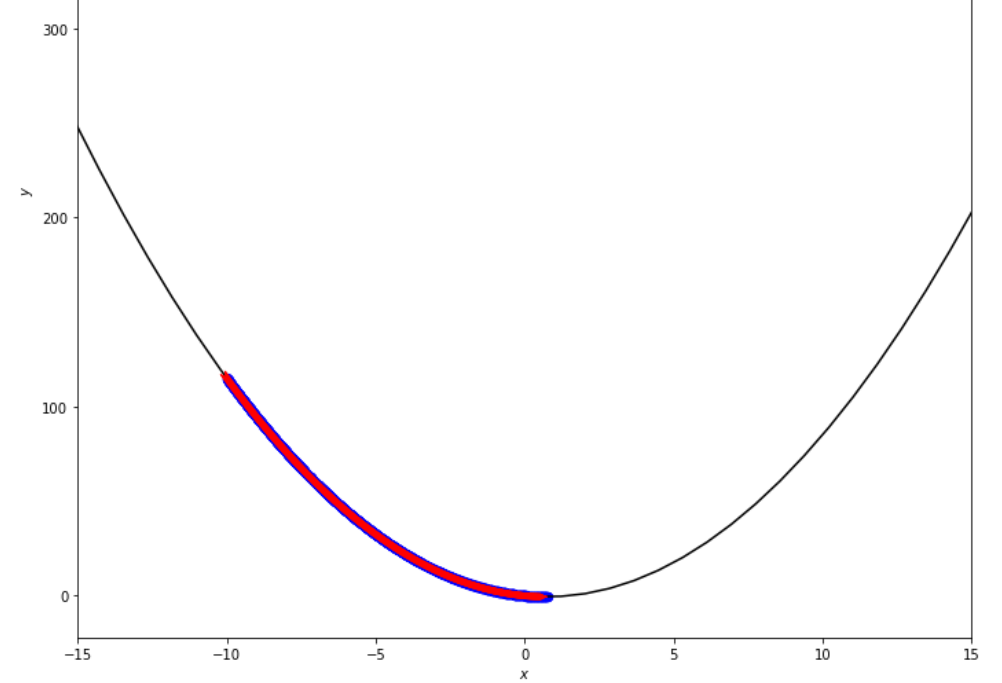

A sequência de medidas tomadas pelo algoritmo de etapa fixa antes de atingir o mínimo

Etapa acelerada

 print ( 'x* =' , soom . accelerated_step ( f , xs , epsilon ))
po2 . accelerated_step ( f , xs , epsilon )

 x* = 0.86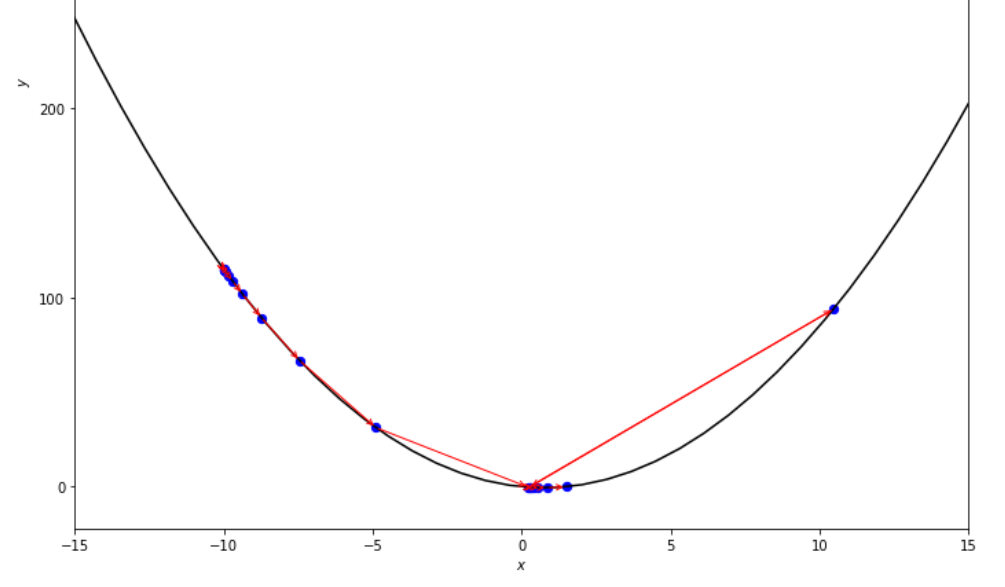

A sequência de medidas tomadas pelo algoritmo de etapa acelerado antes de atingir o mínimo

Pesquisa exaustiva

 print ( 'x* =' , soom . exhaustive_search ( f , xs , xf , epsilon ))
po2 . exhaustive_search ( f , xs , xf , epsilon )

 x* = 0.75

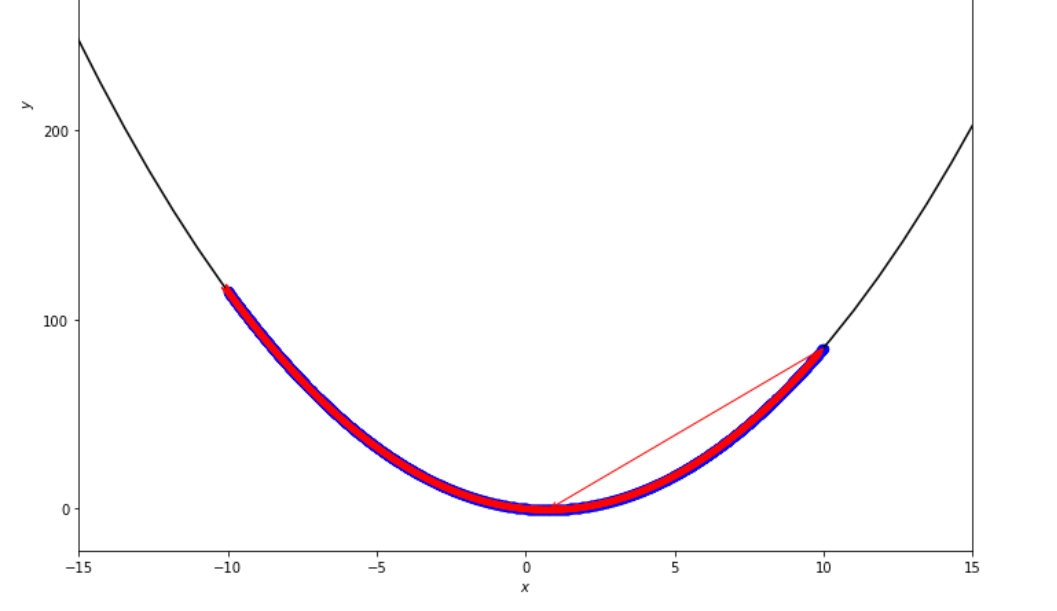
A sequência de medidas tomadas pelo algoritmo de pesquisa exaustiva antes de atingir o mínimo

Pesquisa dicotômica

 mini_delta = 1.e-3
print ( 'x* =' , soom . dichotomous_search ( f , xs , xf , epsilon , mini_delta ))
po2 . dichotomous_search ( f , xs , xf , epsilon , mini_delta )

 x* = 0.7494742431640624

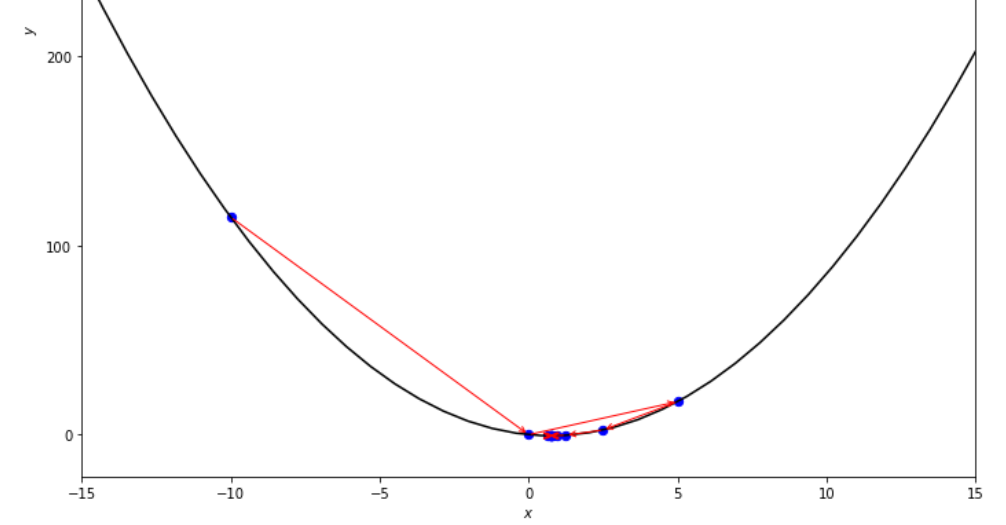
A sequência de medidas tomadas pelo algoritmo de pesquisa dicotômica antes de atingir o mínimo

Intervalo pela metade da metade

 print ( 'x* =' , soom . interval_halving ( f , xs , xf , epsilon ))
po2 . interval_halving ( f , xs , xf , epsilon )

 x* = 0.75

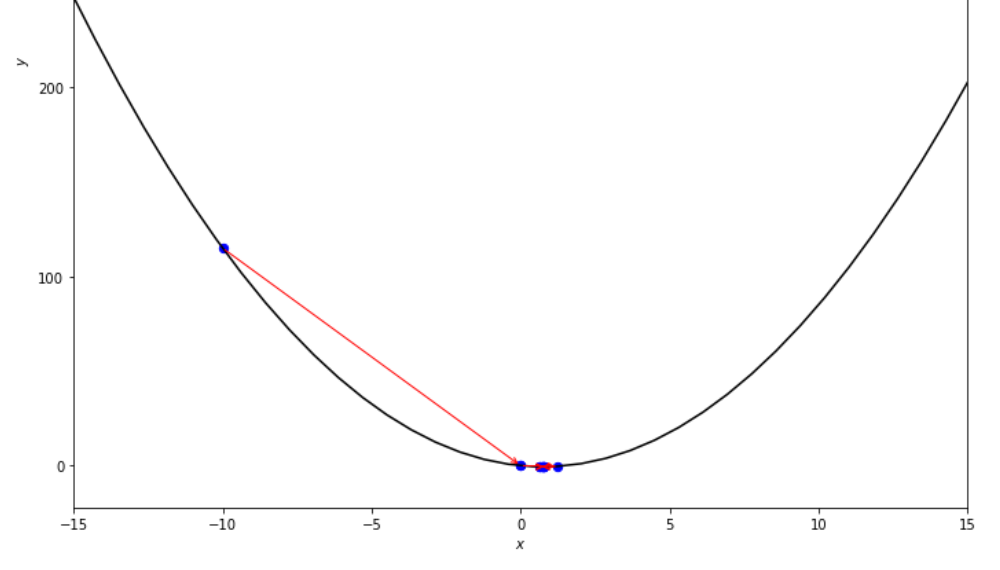
A sequência de etapas tomadas pelo algoritmo intervalo pela metade antes de atingir o mínimo.

Fibonacci

 n = 15
print ( 'x* =' , soom . fibonacci ( f , xs , xf , n )) 
po2 . fibonacci ( f , xs , xf , n )

 x* = 0.76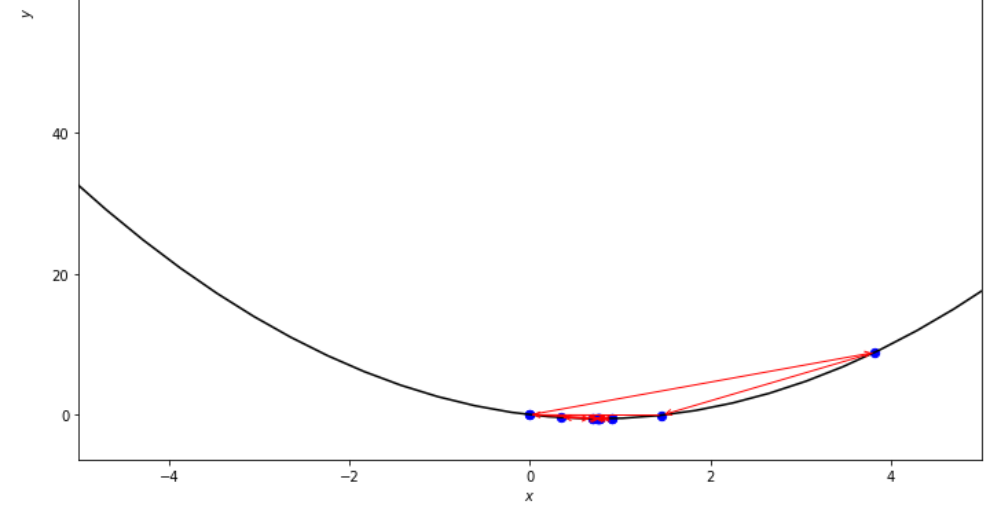

A sequência de etapas tomadas pelo algoritmo Fibonacci antes de atingir o mínimo.

Seção de ouro

 print ( 'x* =' , soom . golden_section ( f , xs , xf , epsilon ))
po2 . golden_section ( f , xs , xf , epsilon )

 x* = 0.75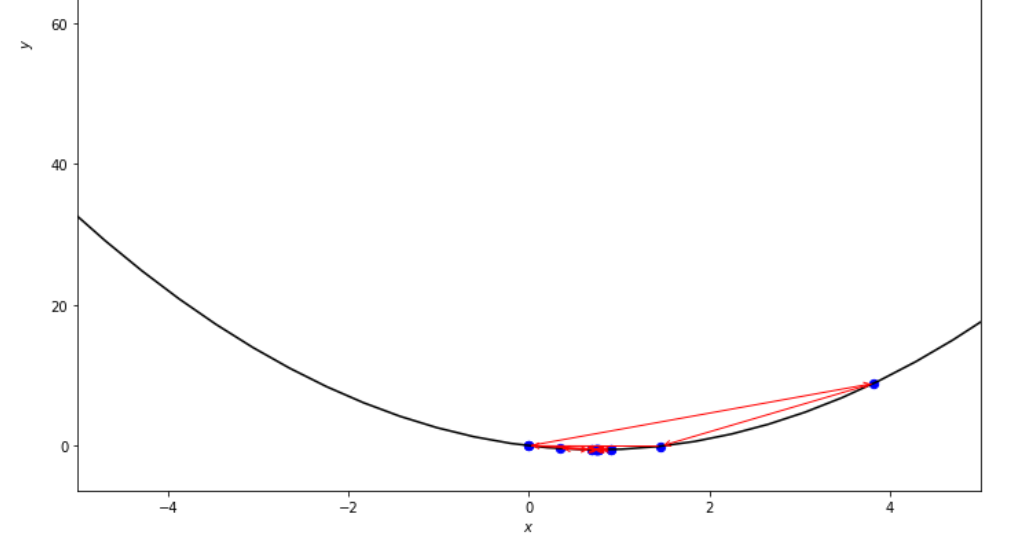

A sequência de medidas tomadas pelo algoritmo da seção de ouro antes de atingir o mínimo

Armijo para trás

 ŋ = 2
xs = 100
print ( 'x* =' , soom . armijo_backward ( f , xs , ŋ , epsilon ))
po2 . armijo_backward ( f , xs , ŋ , epsilon )

 x* = 0.78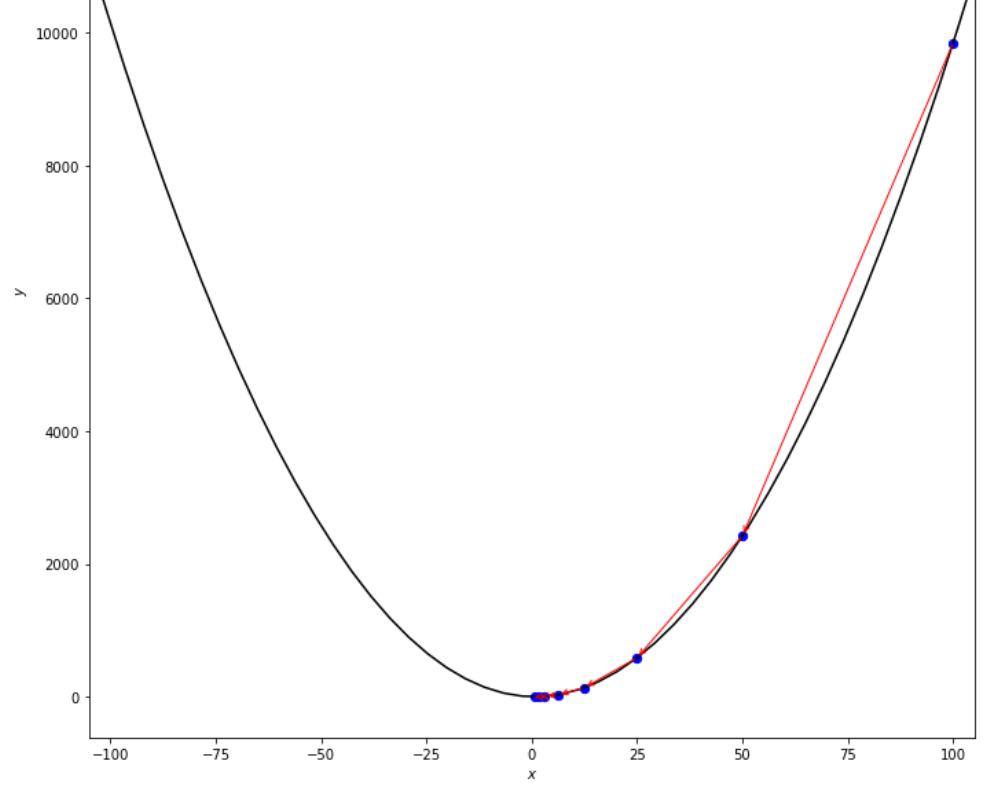

A sequência de medidas tomadas pelo algoritmo para trás do Armijo antes de atingir o mínimo

Armijo para a frente

 xs = 0.1
epsilon = 0.5
ŋ = 2
print ( 'x* =' , soom . armijo_forward ( f , xs , ŋ , epsilon ))
po2 . armijo_forward ( f , xs , ŋ , epsilon )

 x* = 0.8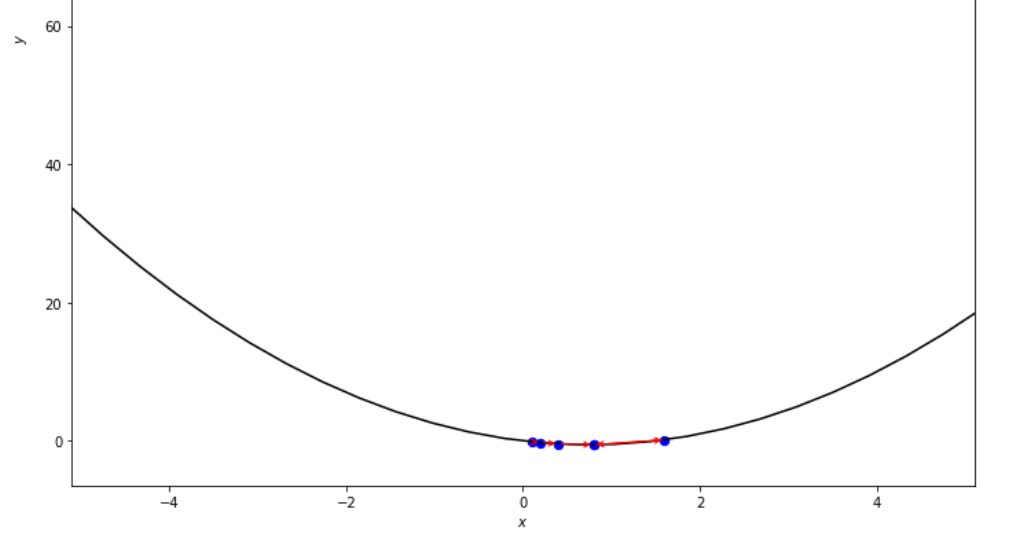

A sequência de medidas tomadas pelo algoritmo de armijo para a frente antes de atingir o mínimo

Análise comparativa

 po2 . compare_all_time ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 )

Tempo de execução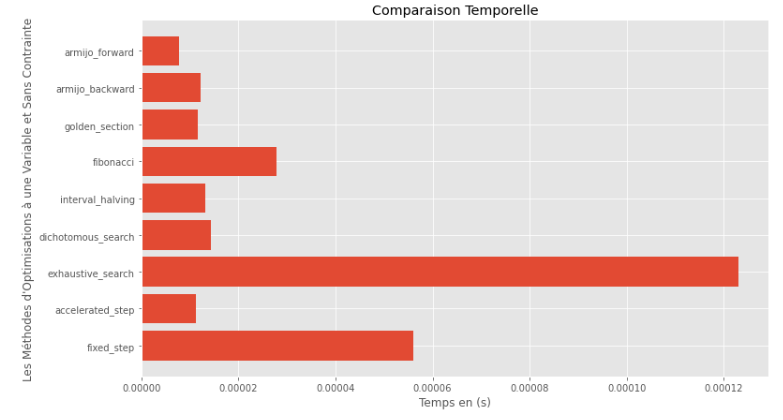

 po2 . compare_all_precision ( f , 0 , 2 , 1.e-2 , 1.e-3 , 10 , 2 , 0.1 , 100 )

Lacuna entre o mínimo verdadeiro e computado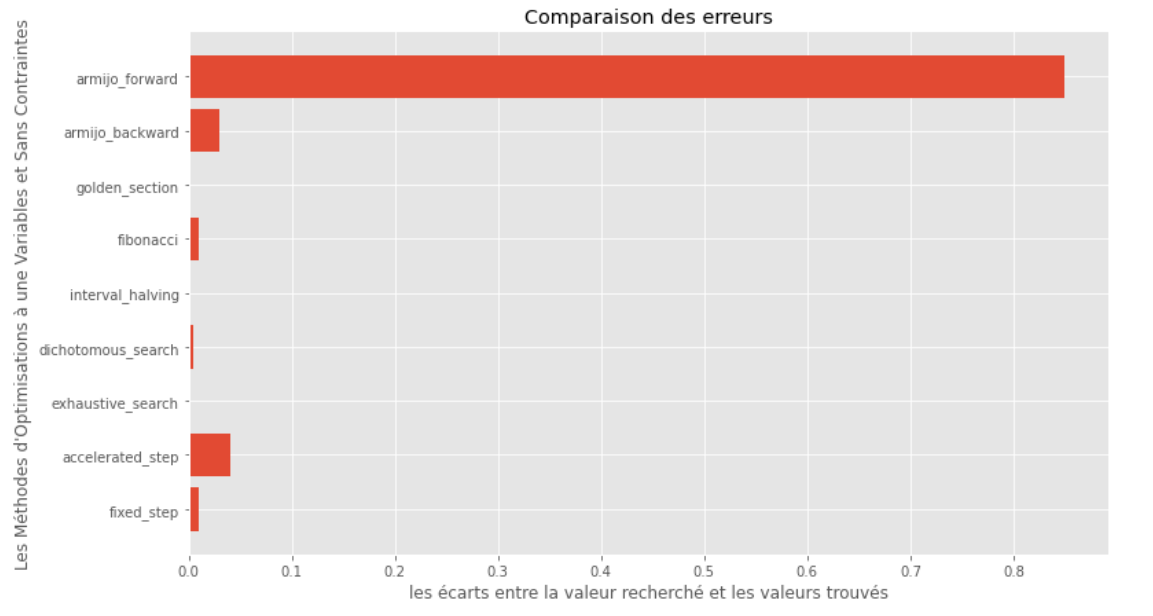

A partir dos gráficos de tempo de execução e precisão, pode-se deduzir que, entre os algoritmos avaliados para essa função convexa de variável única, o método da seção dourada surge como a escolha ideal, oferecendo uma mistura de alta precisão e tempo de execução notavelmente baixo.

Algoritmos de otimização multivariável

Importação de bibliotecas

 import pyoptim . my_plot . multivar . _3D as pm3
import pyoptim . my_plot . multivar . contour2D as pmc

Função objectif

 def h ( x ):
    return x [ 0 ] - x [ 1 ] + 2 * ( x [ 0 ] ** 2 ) + 2 * x [ 1 ] * x [ 0 ] + x [ 1 ] ** 2
# analytically, argmin(f) = [-1, 1.5]

solução analítica

Inicialização do parâmetro

 X = [ 1000 , 897 ]
alpha = 1.e-2
tol = 1.e-2

Descendência de gradiente

 pmc . gradient_descent ( h , X , tol , alpha )
pm3 . gradient_descent ( h , X , tol , alpha )

 Y* =  [-1.01  1.51]

A sequência de medidas tomadas pelo algoritmo de descida de gradiente antes de atingir o mínimo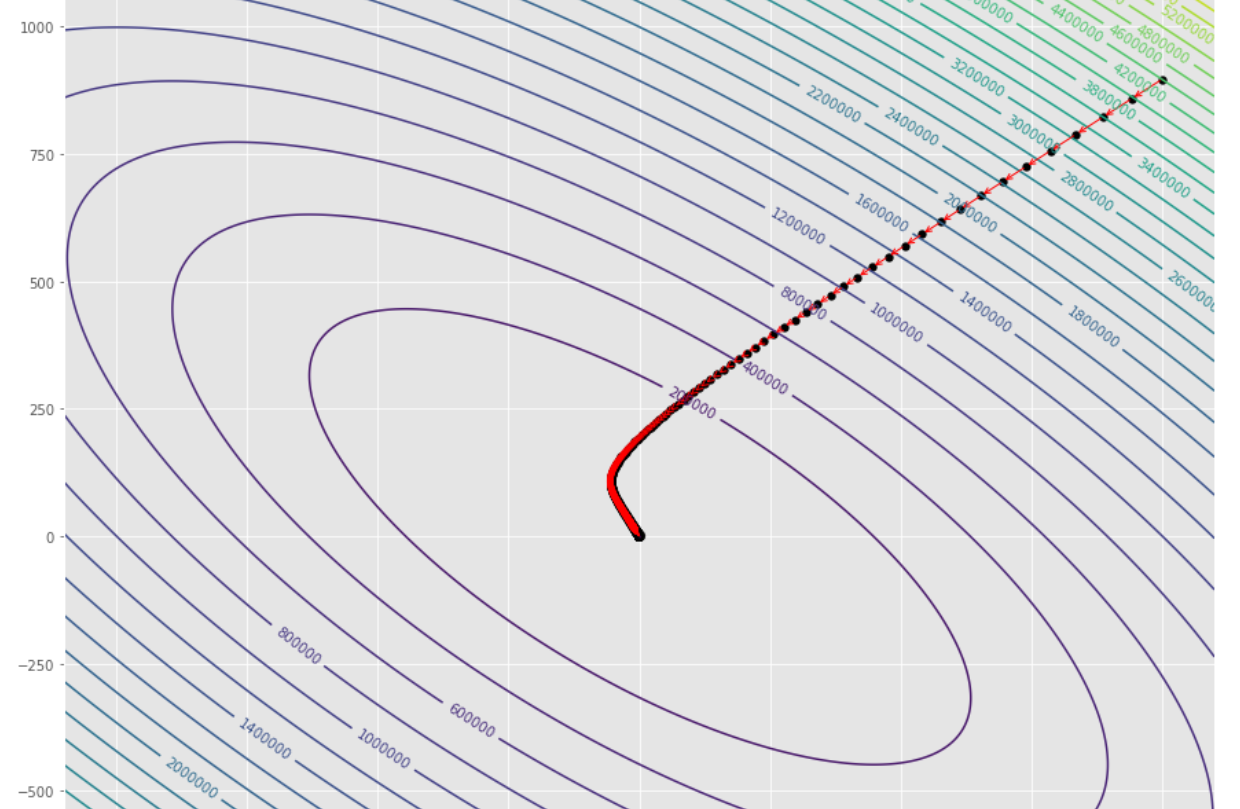

Lote de contorno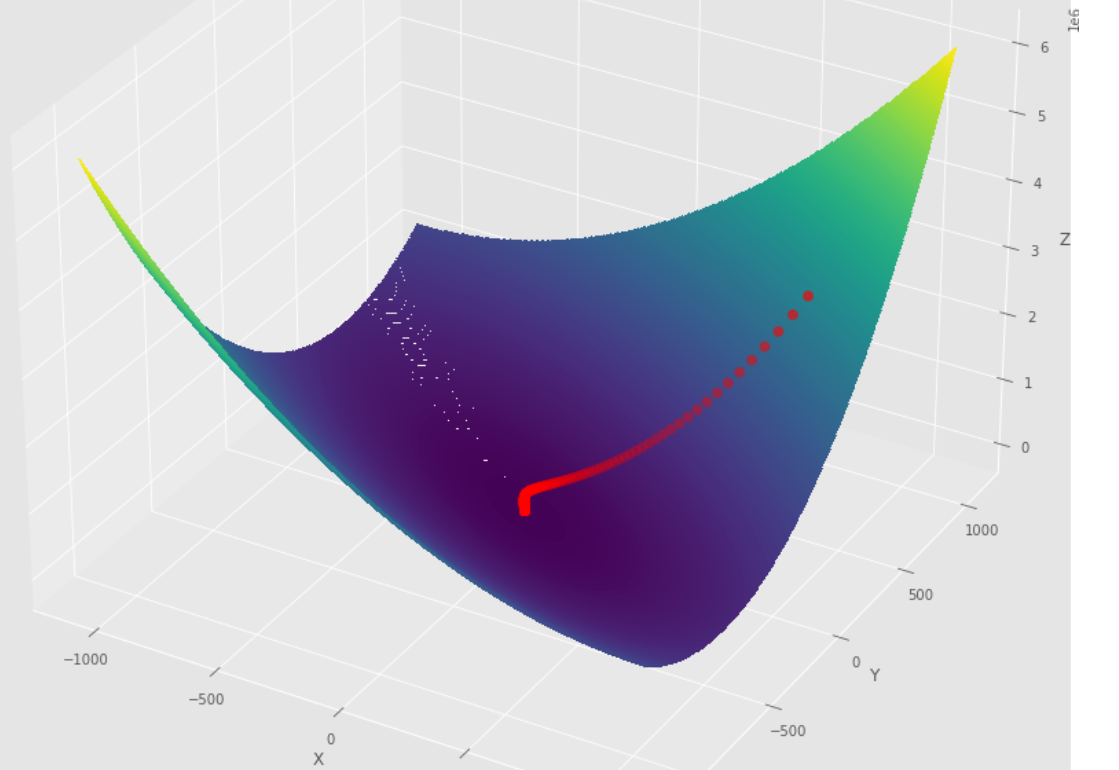

Lote 3D

Conjugado de gradiente

 pmc . gradient_conjugate ( h , X , tol )
pm3 . gradient_conjugate ( h , X , tol )

 Y* =  [-107.38  172.18]

A sequência de medidas tomadas pelo algoritmo conjugado de gradiente antes de atingir o mínimo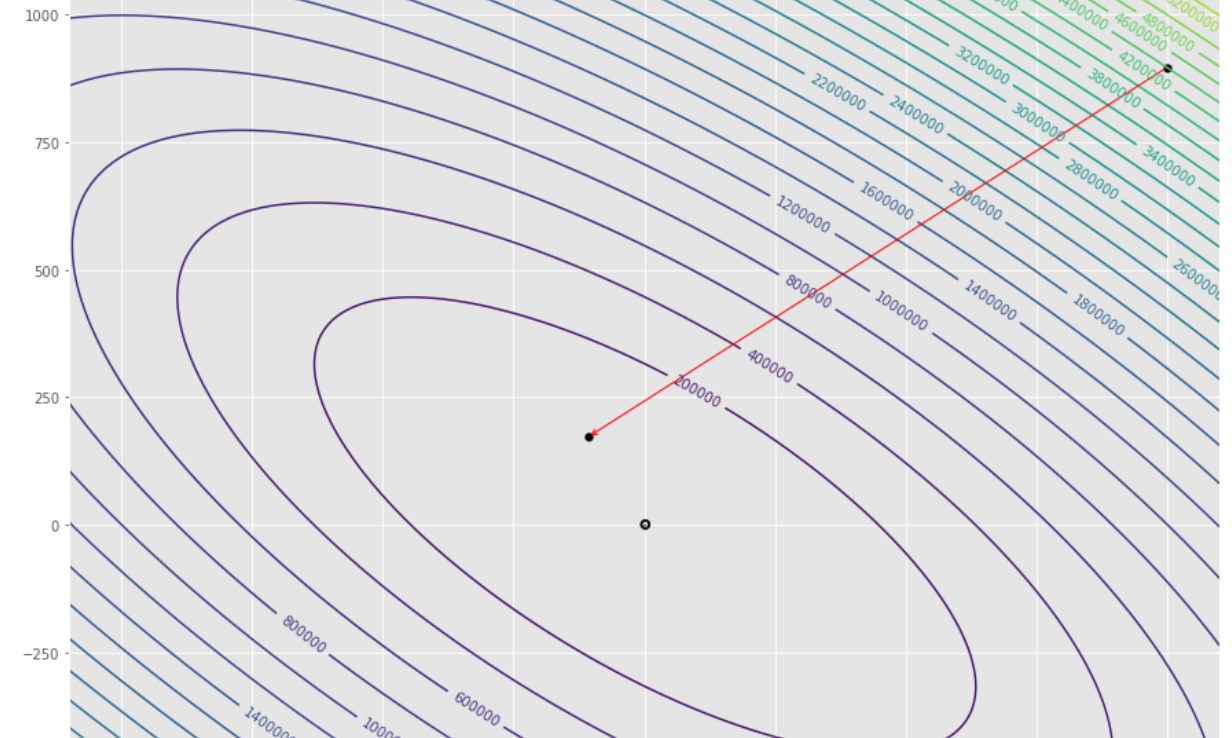

Lote de contorno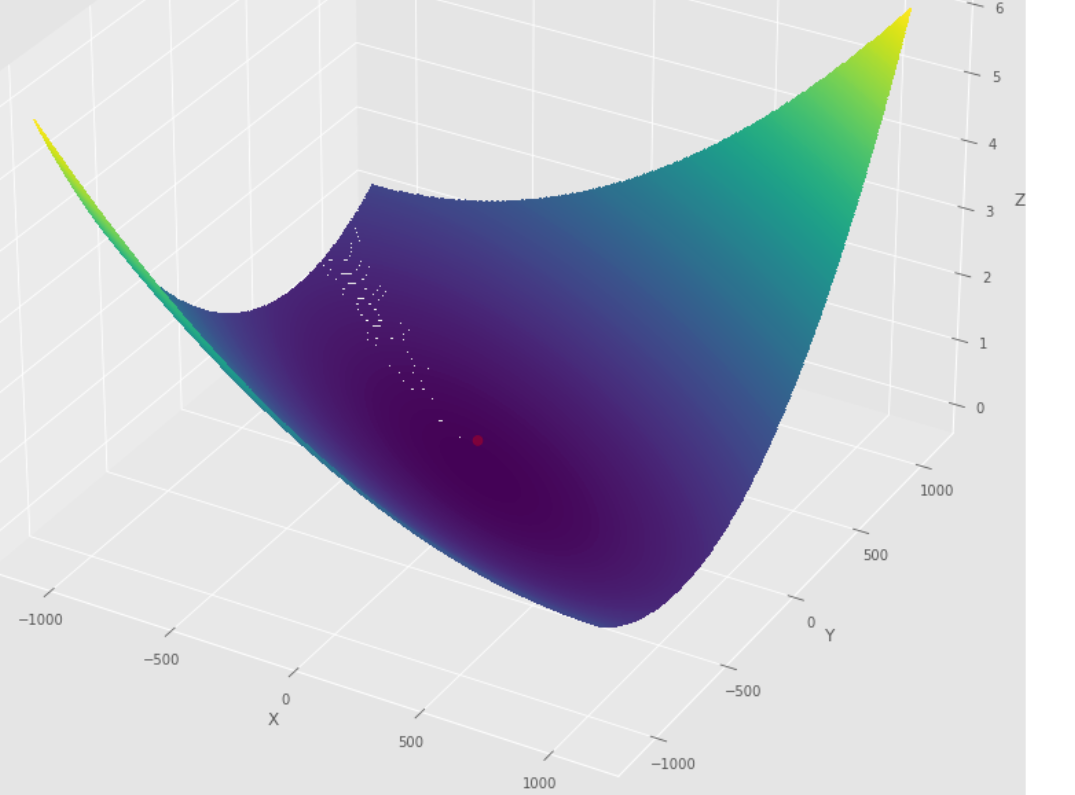

Lote 3D

Newton

 pmc . newton ( h , X , tol )
pm3 . newton ( h , X , tol )

 Y* =  [-1.   1.5]

A sequência de medidas tomadas pelo algoritmo Newton antes de atingir o mínimo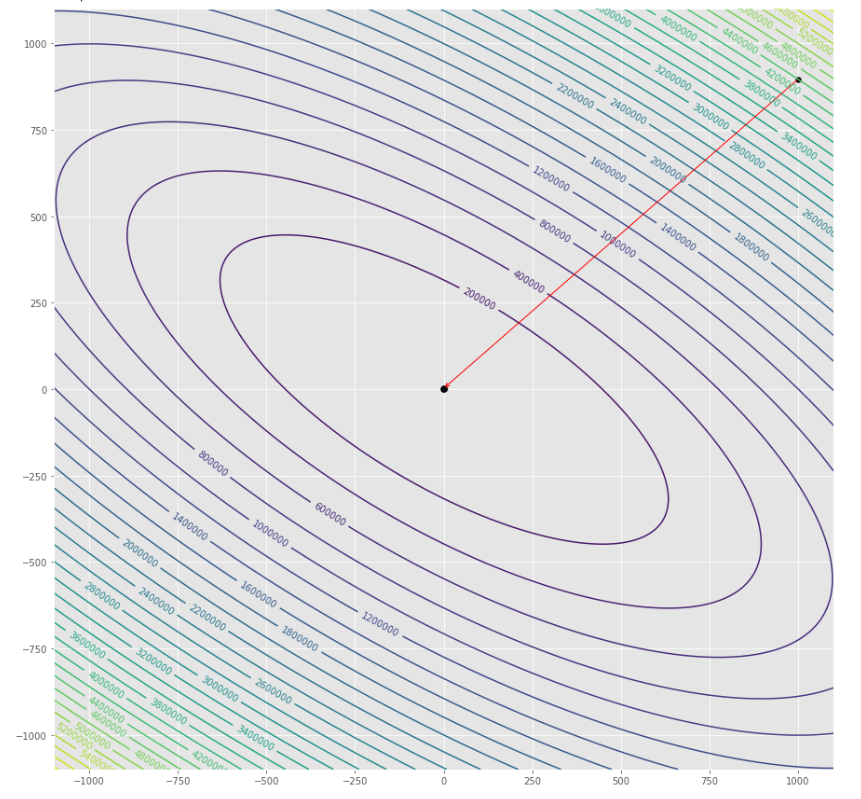

Lote de contorno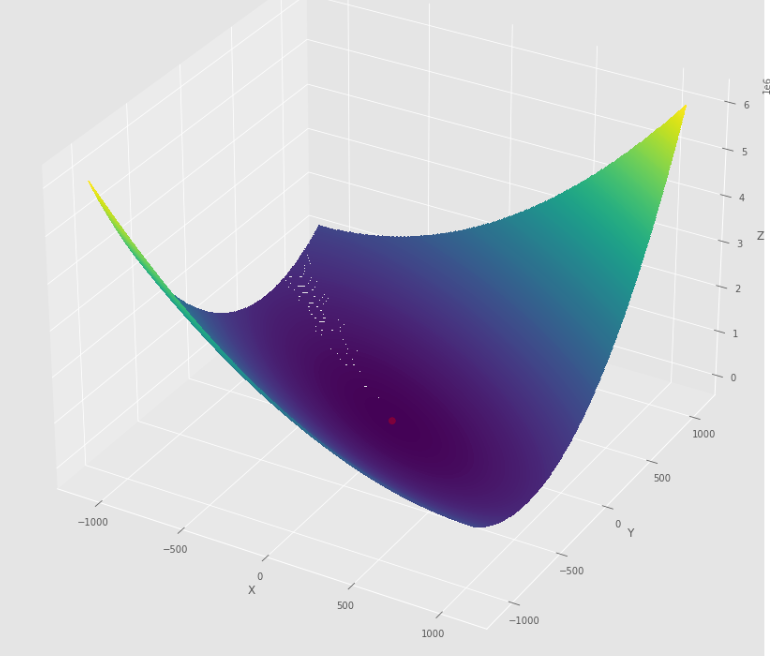

Lote 3D

Quasi Newton DFP

 pmc . quasi_newton_dfp ( h , X , tol )
pm3 . quasi_newton_dfp ( h , X , tol )

 Y* =  [-1.   1.5]

A sequência de medidas tomadas pelo algoritmo quase newton dfp antes de atingir o mínimo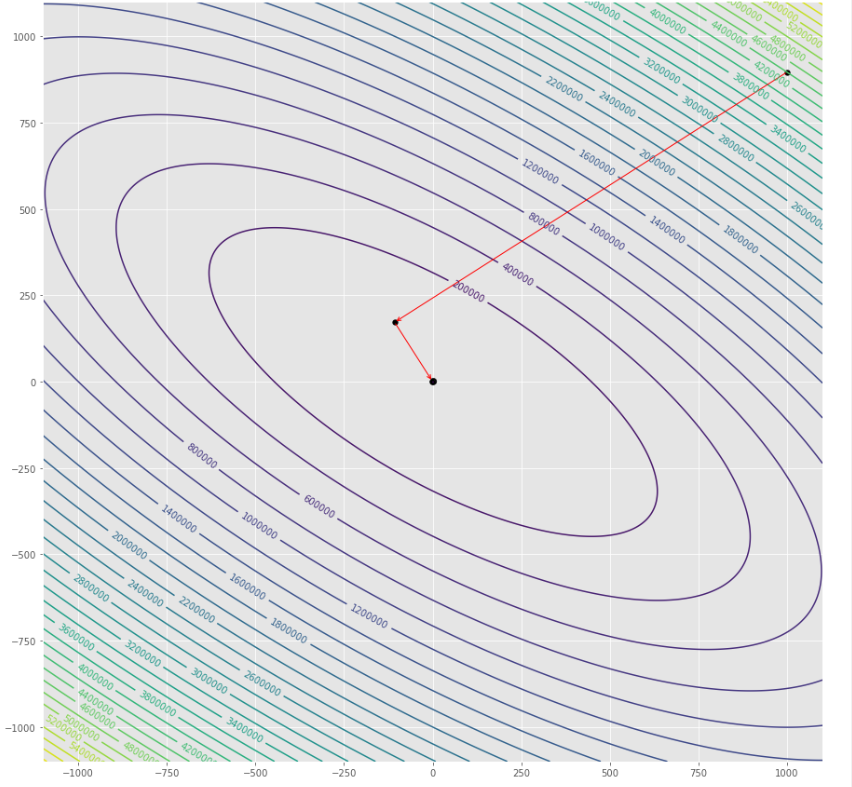

Lote de contorno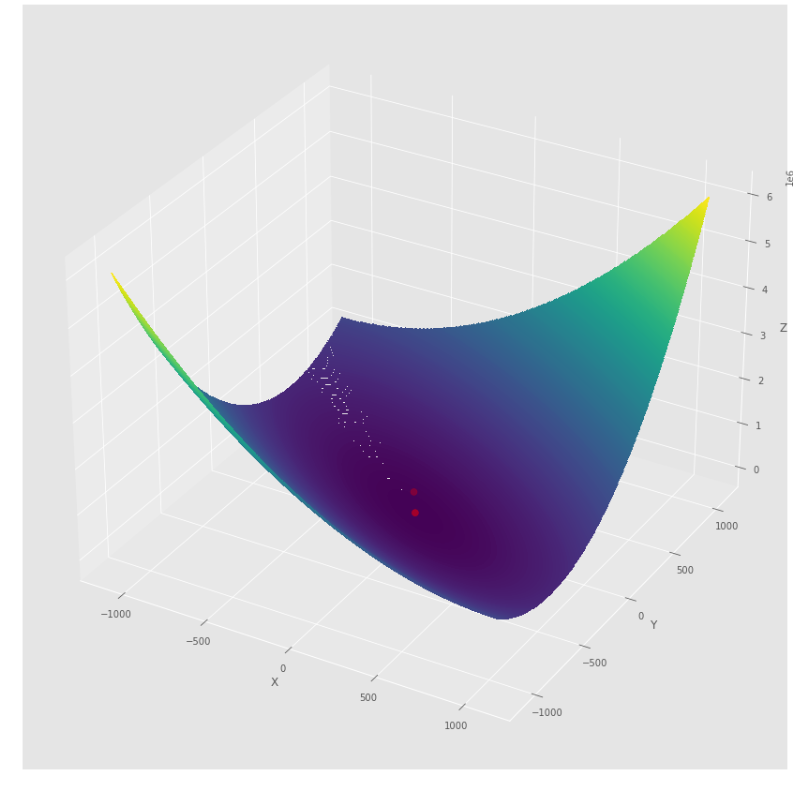

Lote 3D

Descendência de gradiente estocástico

 pmc . sgd ( h , X , tol , alpha )
pm3 . sgd ( h , X , tol , alpha )

 Y* =  [-1.01  1.52]

A sequência de medidas tomadas pelo algoritmo de descida de gradiente estocástico antes de atingir o mínimo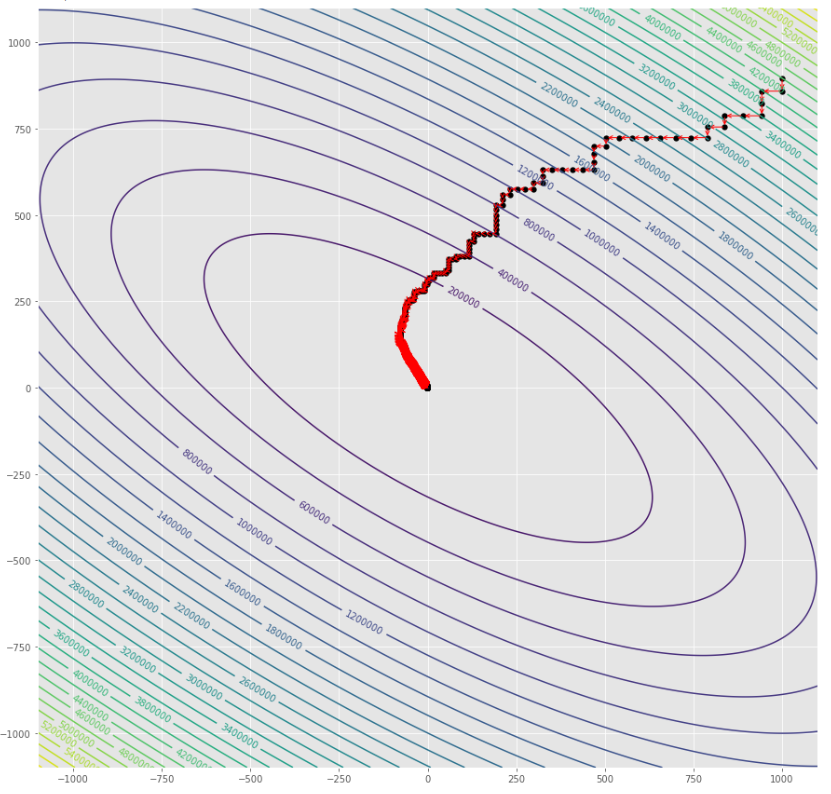

Lote de contorno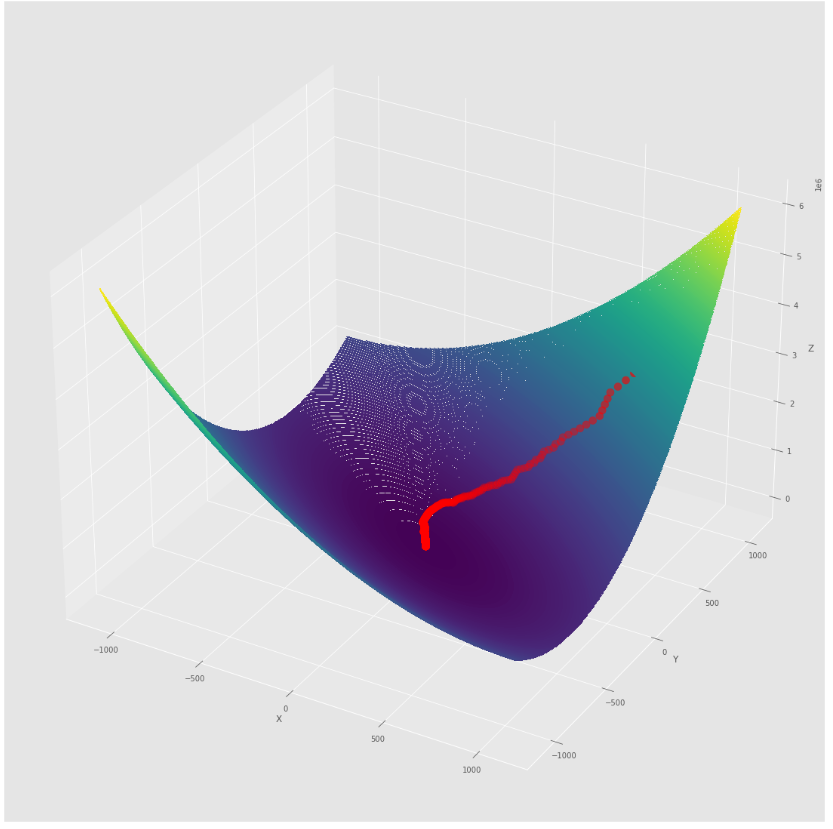

Lote 3D

Descendência de gradiente estocástica com BLS

 alpha = 100 #it must be high because of BLS
c = 2
pmc . sgd_with_bls ( h , X , tol , alpha , c ) 
pm3 . sgd_with_bls ( h , X , tol , alpha , c )

 Y* =  [-1.   1.5]

A sequência de medidas tomadas pela descida de gradiente estocástica com o algoritmo BLS antes de atingir o mínimo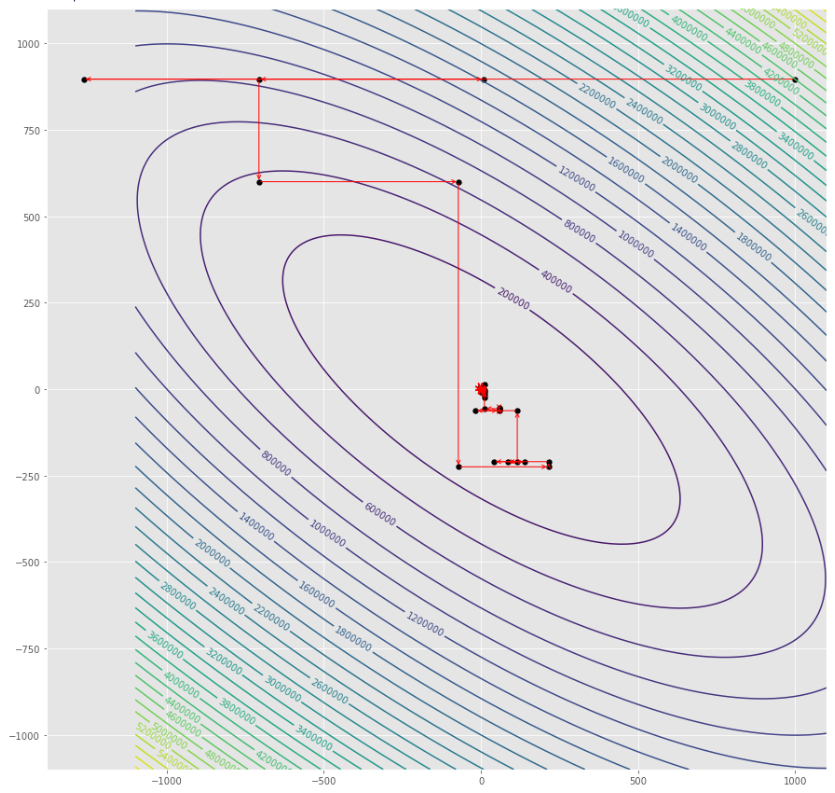

Lote de contorno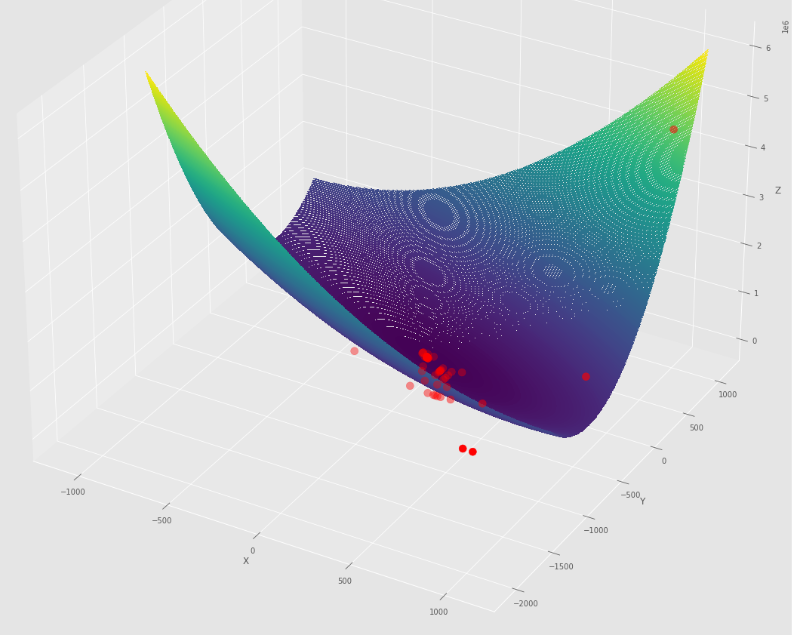

Lote 3D

Análise comparativa

 pm3 . compare_all_time ( h , X , 1.e-2 , 1.e-1 , 100 , 2 )

Tempo de execução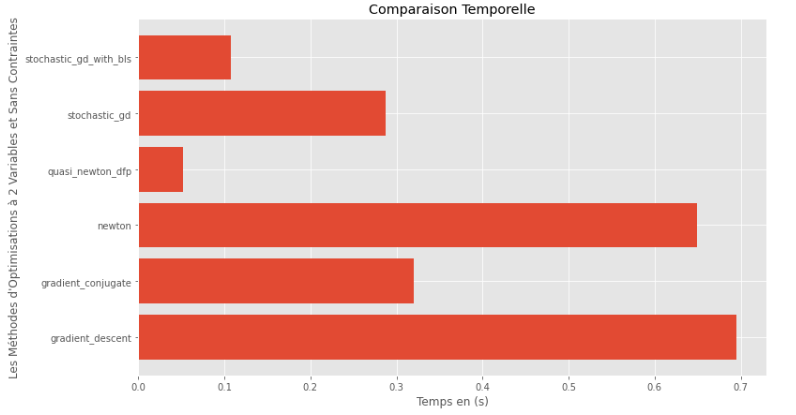

 pm3 . compare_all_precision ( h , X , 1.e-2 , 1.e-1 , 100 , 2 )

Lacuna entre o mínimo verdadeiro e computado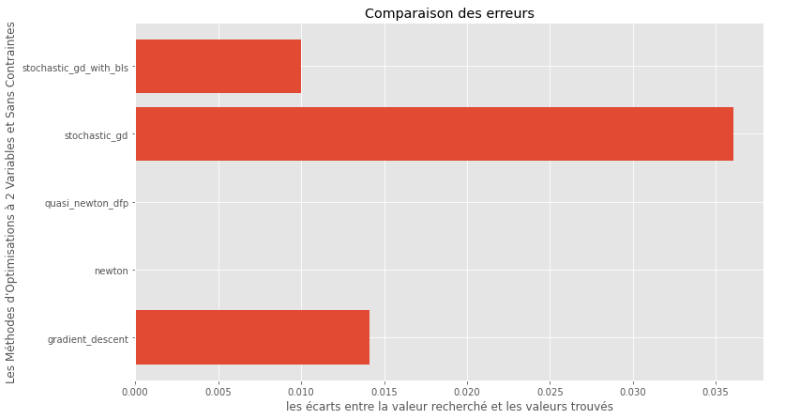

A partir dos gráficos de tempo de execução e precisão, pode -se deduzir que, entre os algoritmos avaliados para essa função multivariável convexa, o método quase Newton DFP surge como a escolha ideal, oferecendo uma mistura de alta precisão e tempo de execução baixa.

Matriz inversa

Bibliotecas de importação

 import pyoptim . my_numpy . inverse as npi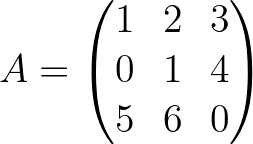

Matriz de teste

 A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]])

Gauss Jordan

 A_1 = npi . gaussjordan ( A . copy ())
I = A @ A_1
I = np . around ( I , 1 )
print ( 'A_1 = n n ' , A_1 )
print ( ' n A_1*A = n n ' , I )

 A_1 =

 [[-24.  18.   5.]
 [ 20. -15.  -4.]
 [ -5.   4.   1.]]

A_1*A =

 [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

Decomposição da matriz

Importações

 import pyoptim . my_numpy . decompose as npd

Matriz de teste

 A = np . array ([[ 1. , 2. , 3. ],[ 0. , 1. , 4. ],[ 5. , 6. , 0. ]])      #A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ],[ - 1. , 2. , - 1. ],[ 0. , - 1. , 2. ]])  #B is positive definite
Y = np . array ([ 45 , - 78 , 95 ])                               #randomly chosen column vector

Lu

 L , U , P = npd . LU ( A )
print ( "P = n " , P , " n n L = n " , L , " n n U = n " , U )
print ( " n " , A == P @ L @ U )

 P =
 [[0. 0. 1.]
 [0. 1. 0.]
 [1. 0. 0.]] 

L =
 [[1.  0.  0. ]
 [0.  1.  0. ]
 [0.2 0.8 1. ]] 

U =
 [[ 5.   6.   0. ]
 [ 0.   1.   4. ]
 [ 0.   0.  -0.2]]

 [[ True  True  True]
 [ True  True  True]
 [ True  True  True]]

Choleski

 L = npd . choleski ( A )          # A is not positive definite
print ( L )
print ( "--------------------------------------------------" )
L = npd . choleski ( B )          # B is positive definite 
print ( 'L = n ' , L , ' n ' )

C = np . around ( L @( L . T ), 1 )
print ( 'B = L@(L.T) n n ' , B == C )

 A must be positive definite !
None
--------------------------------------------------
L =
 [[ 1.41421356  0.          0.        ]
 [-0.70710678  1.22474487  0.        ]
 [ 0.         -0.81649658  1.15470054]] 

B = L@(L.T) 

 [[ True  True  True]
 [ True  True  True]
 [ True  True  True]]

Resolvendo sistemas lineares

Importações

 import pyoptim . my_numpy . solve as nps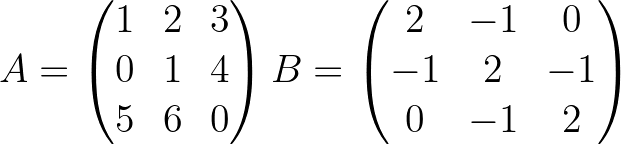

Matriz de teste

 A = np . array ([[ 1. , 2. , 3. ], [ 0. , 1. , 4. ], [ 5. , 6. , 0. ]]) # A is not positive definite
B = np . array ([[ 2. , - 1. , 0. ], [ - 1. , 2. , - 1. ], [ 0. , - 1. , 2. ]]) # B is positive definite
Y = np . array ([ 45 , - 78 , 95 ]) # randomly chosen column vector

Gauss Jordan

 X = nps . gaussjordan ( A , Y )
print ( "X = n " , X )
print ( " n A@X=Y n " , A @ X == Y , ' n ' )

print ( '---------------------------------------------------------------' )
X = nps . gaussjordan ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n B@X=Y n " , Y_ == Y , ' n ' )

 X =
 [[-2009.]
 [ 1690.]
 [ -442.]]

 A@X=Y 
 [[ True]
 [ True]
 [ True]] 

---------------------------------------------------------------
X =
 [[18.5]
 [-8. ]
 [43.5]]

 B@X=Y 
 [[ True]
 [ True]
 [ True]]

Lu

 X = nps . LU ( A , Y )
print ( "X* = n " , X )
print ( " n AX*=Y n " , A @ X == Y )
print ( "-------------------------------------------------------------------------------" );
X = nps . LU ( B , Y )
print ( "X* = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y )

 X* =
 [[-2009.]
 [ 1690.]
 [ -442.]]

AX*=Y 
 [[ True]
 [ True]
 [ True]]
-------------------------------------------------------------------------------
X* =
 [[18.5]
 [-8. ]
 [43.5]]

BX*=Y
 [[ True]
 [ True]
 [ True]]

Choleski

 X = nps . choleski ( A , Y )
print ( "-------------------------------------------------------------------------------" )
X = nps . choleski ( B , Y )
print ( "X = n " , X )
Y_ = np . around ( B @ X , 1 )
print ( " n BX*=Y n " , Y_ == Y )

 !! A must be positive definite !!
-------------------------------------------------------------------------------
X =
 [[18.5]
 [-8. ]
 [43.5]]

BX*=Y
 [[ True]
 [ True]
 [ True]]

Expandir