fastest lap

Самый быстрый круг ??

Самый быстрый кружок-это симулятор динамики автомобиля. Его можно использовать, чтобы понять динамику транспортных средств, чтобы узнать о методах вождения, для разработки прототипов автомобилей или просто для удовольствия!

Что можно сделать

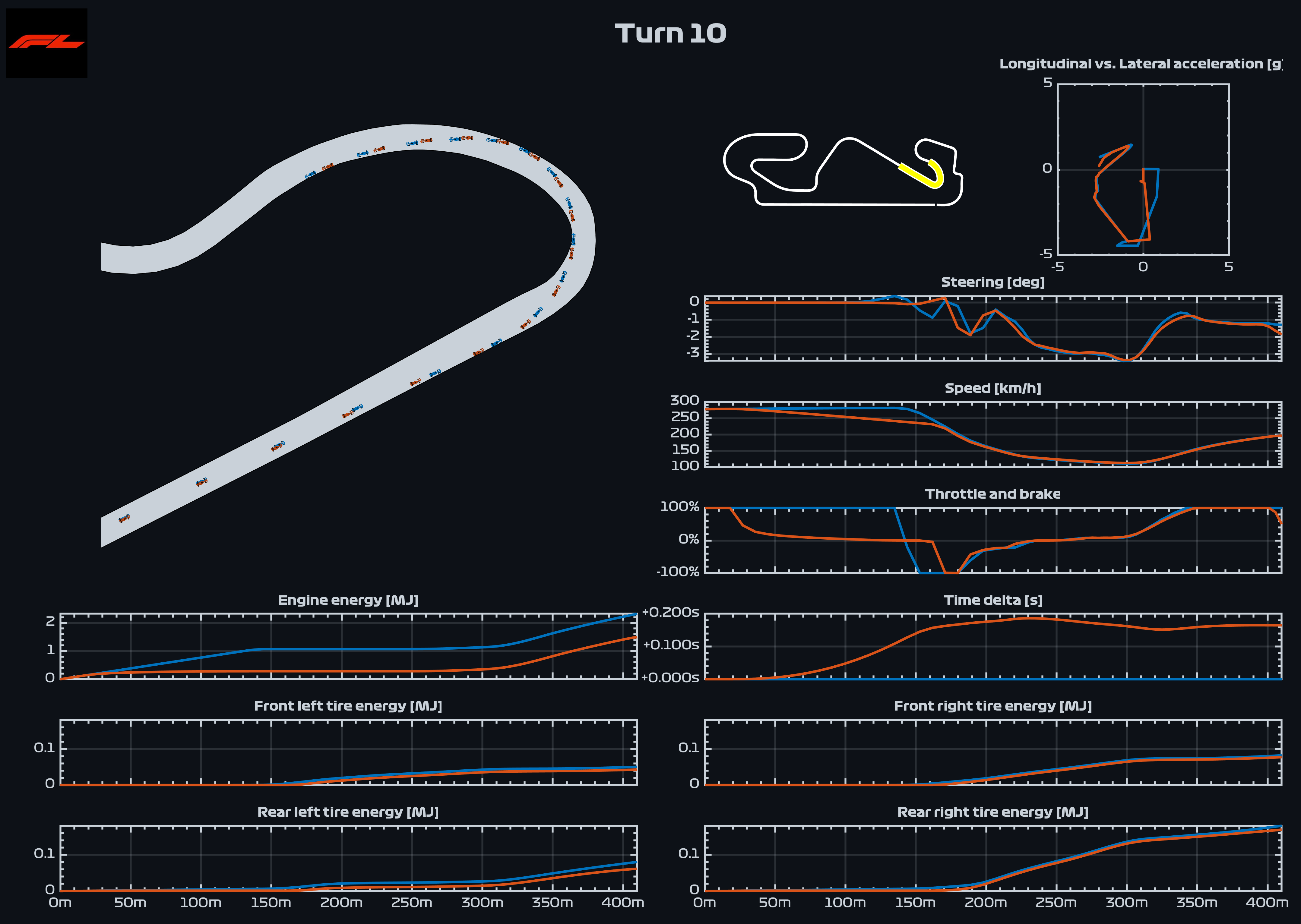
• Численная диаграмма GG: с учетом транспортного средства и скорости для вычисления его диаграммы Ax-AY. Диаграмма GG является полезным методом в области дизайна транспортных средств и разведки параметров.

  Это решается как проблема оптимизации: для данного бокового ускорения найдите минимальное/максимальное возможное продольное ускорение.

• Оптимальное моделирование номера: с учетом транспортного средства и схемы для вычисления оптимальных элементов управления, которые минимизируют ночное время.

  Эта проблема решается с использованием метода коллокации первого порядка, трапециевидного правила, с методами более высокого порядка, планируемых в ближайшее время. NLP решается с использованием IPOPT, и CPPAD для повышения его производительности (время круга вокруг цепь DE Catalunya может быть получено с 500 точками примерно за 1 минуту).

  Это не квази-устроенное симуляцию. Модель решает полностью переходные состояния, как в динамических уравнениях без устойчивых допущений.

Ferrari-2012-australia.mp4

Подход

Ядро программного обеспечения - библиотека C ++, которую можно использовать через Python API. Полная документация еще не доступна, но некоторые примеры можно найти в примерах/Python. Самый быстрый кружок очень эффективен, способный вычислить полный оптимальный круг менее чем за 1 минуту.

Динамические модели

Код реализует две модели автомобилей:

• Модель автомобиля 3DOF (продольная, боковая и рыскание), в настоящее время используется для моделирования F1. Используемые параметры по умолчанию можно найти в ./database/limebeer-2014-f1.xml
• Модель автомобиля 6DOF (продольная, боковая, вертиальная, рыскание, высота и рулон), в настоящее время используется для моделирования Go-Kart. Используемые параметры по умолчанию можно найти в ./database/roberto-lot-2016-kart.xml

Схемы

Схемы смоделированы из путей, созданных из Google Earth, например, правильный предел отслеживания каталонии включен в этот репозиторий (Database/Google_earth/Catalunya_right.kml). Затем схемы предварительно обрабатываются инструментом, включенным в данном документе для извлечения эталонной линии, ее кривизны и расстояния до предела левой/правой дорожки (база данных/Catalunya_discrete.xml).

Зависимости

Самая быстрая круга использует несколько библиотек с открытым исходным кодом:

• IPOPT: Interior Point Optimizer, является программным пакетом с открытым исходным кодом для крупномасштабной нелинейной оптимизации. Используется в этом проекте для получения решения оптимальных задач в области номера, написанных как НЛП (нелинейная проблема программирования).
• CPPAD: C ++ Алгоритмическая дифференциация. Распределенный вместе с IPOPT, он используется для расчета аналитических производных.
• Tinyxml2: tinyxml-2-это простой, малый, эффективный, C ++ XML-анализатор, используемый для чтения файлов XML (например, параметры модели, треки, ...)
• Logger-CPP: простой регистратор в C ++, чтобы обрабатывать уровни печати и другие интересные дополнения
• Lion-CPP: LightWeigh Interfaces для оптимизации и чисел, диспетчер пакетов C ++ для всех библиотек, упомянутых выше, плюс другие численные методы, такие как механические рамы, векторная алгебра и Runge-Kutta схемы

Установка

Windows 10

Предварительные двоичные файлы доступны для загрузки для каждого выпуска.

• v0.1
• v0.2
• v0.3
• v0.4
• v0.5

Скачать и раскапывать. Содержимое папки ZIP:

• BIN: Динамические библиотеки. Самый быстрый кружок C ++ Core есть. Если из Matlab используется наиболее быстрое кружок, точка loadlibrary() в этот каталог.
• Включите: FastestLapc.H и Fastest_lap.py. Чтобы использовать сценарии Python, убедитесь, что эта папка находится на PYTHONPATH
• Примеры: Примеры ноутбуков Python.
• База данных: данные автомобиля и отслеживания

Mac и Linux

Этот проект использует Cmake для создания исходного кода и производства двоичных файлов.

Канонические шаги для компиляции проекта Cmake: (Предположим, что $FASTESTLAP - верхний уровень исходного кода.)

1. Создайте папку сборки.

 mkdir ${FASTESTLAP}/build

2. Из папки сборки запустите Cmake

 cd ${FASTESTLAP}/build && cmake ..

Варианты, доступные для Cmake:

 -DCMAKE_BUILD_TYPE=Debug/Release
-DCMAKE_INSTALL_PREFIX=/path/to/install/dir
-DCODE_COVERAGE=Yes/No: enables code coverage (if so, use with -DCMAKE_BUILD_TYPE=Debug)
-DBUILD_DOC=Yes/No: builds doxygen documentation

На этом этапе Cmake загрузит и установит все сторонние зависимости.

3. Компиляция

 make

4. Тест (необязательно, но рекомендуется)

 ctest --verbose

5. Установить (необязательно)

 make install

Linux

Предоставлена ​​среда сборки Docker и может использоваться для составления общей библиотеки и генерации привязки Python.

sh ./src/scripts/linux/docker_compile.sh

Документация

Прочитайте последнюю онлайн-документацию по самым быстрым кружке

Ссылки

[1] Тремлетт, AJ и DJN Limebeer. «Оптимальное использование шин для автомобиля Формулы -1». Динамика системы транспортных средств 54.10 (2016): 1448-1473.
[2] Лот, Роберто и Никола Дал Бьянко. «Оптимизация времени круга гоночной карты». Динамика системы транспортных средств 54.2 (2016): 210-230.
[3] Дал Бьянко, Никола, Роберто Лот и Марко Гадола. «Минимальное оптимальное моделирование управления временем гоночного автомобиля GP2». Материалы института инженеров-механиков, часть D: Журнал автомобильной техники 232.9 (2018): 1180-1195.
[4] Лот, Роберто и Маттео Массаро. «Символический подход к моделированию мультизатора дорожных транспортных средств». Международный журнал прикладной механики 9.05 (2017): 1750068.
[5] Келли, Даниэль П. и Робин С. Шарп. «Временный оптимальный контроль над гоночным автомобилем: числовой метод подражания идеальному водителю». Динамика системы транспортных средств 48.12 (2010): 1461-1474.
[6] Пикцинини, Маттия. «Планирование пути и контроль транспортных средств самостоятельного вождения в пределах обработки»
[7] Казанова Д. «При минимальном времени маневрирование транспортных средств: теоретический оптимальный круг»
[8] Perantoni, G. et al. «Оптимальное управление автомобилем Формулы -1 с переменными параметрами»