fastest lap

Schnellste Runde?

Die schnellste Runde ist ein Fahrzeugdynamiksimulator. Es kann verwendet werden, um die Fahrzeugdynamik zu verstehen, über Fahrtechniken zu lernen, Autoprototypen zu entwerfen oder nur zum Spaß!

Was kann getan werden

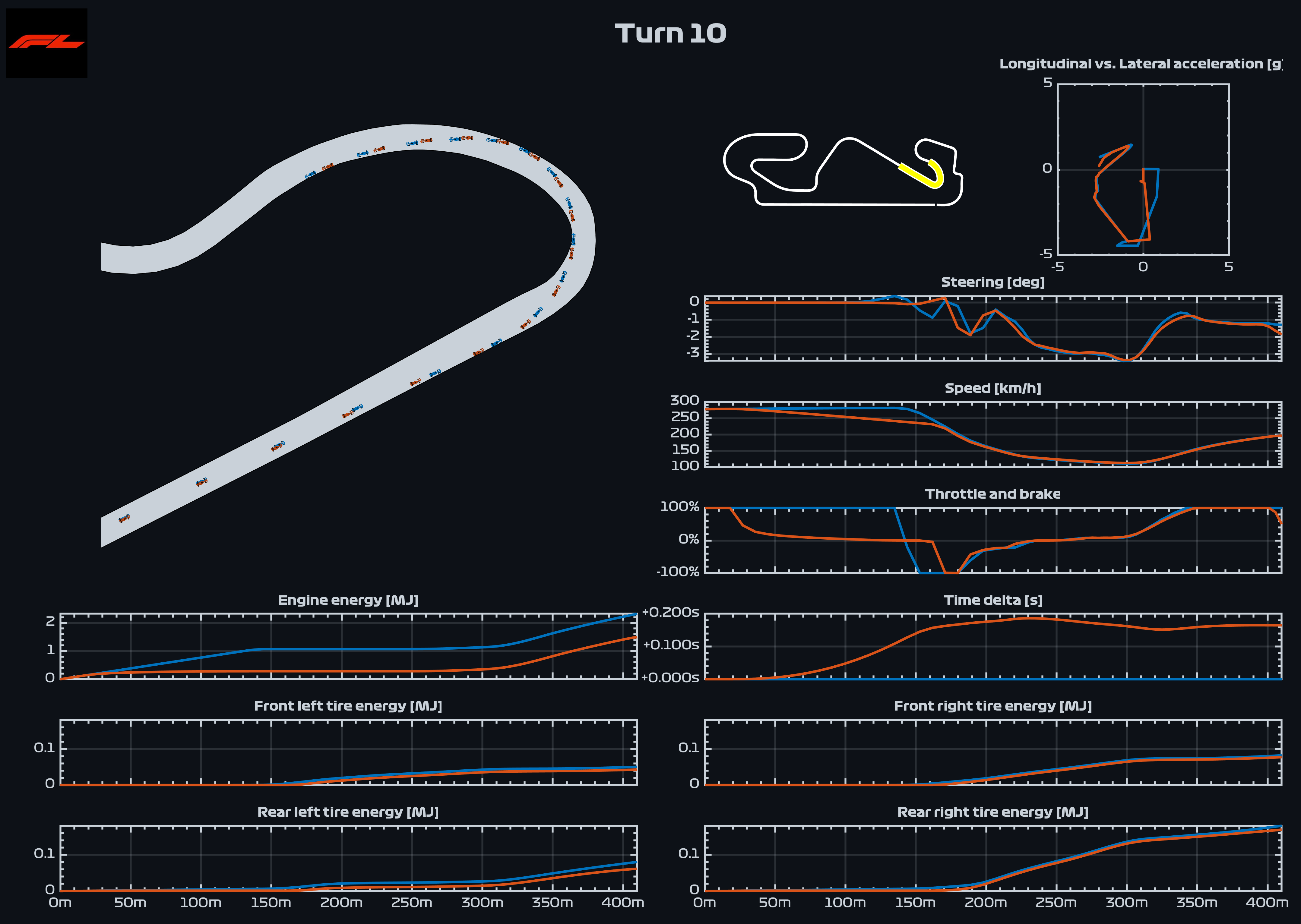
• Numerisches GG-Diagramm: Bei einem Fahrzeug und einer Geschwindigkeit, um sein AX-Ay-Diagramm zu berechnen. Das GG -Diagramm ist eine nützliche Technik bei der Erforschung des Fahrzeugdesigns und der Parameter.

  Dies wird als Optimierungsproblem gelöst: Finden Sie für eine gegebene laterale Beschleunigung die minimale/maximale realisierbare Längsbeschleunigung.

• Optimale Laptime -Simulation: Bei einem Fahrzeug und einer Schaltung die optimalen Steuerelemente berechnet, die die Laptime minimieren.

  Dieses Problem wird unter Verwendung einer Kollokationsmethode erster Ordnung, der Trapezregel, gelöst, wobei die Methoden höherer Ordnung bald implementiert werden sollen. Der NLP wird mit Ipopt und CPPAD gelöst, um seine Leistung zu verbessern (eine Rundenzeit um Circuit de Catalunya kann mit 500 Punkten in ungefähr 1 Minute erhalten werden).

  Dies ist keine quasi-stationäre Simulation. Das Modell löst die vollständig transienten Zustände wie in den dynamischen Gleichungen ohne Annahmen im stationären Zustand.

Ferrari-2022-australia.mp4

Der Ansatz

Der Kern der Software ist eine C ++ - Bibliothek, die über eine Python -API verwendet werden kann. Eine vollständige Dokumentation ist noch nicht verfügbar, aber einige Beispiele finden Sie in Beispielen/Python. Die schnellste Runde ist sehr effizient und kann in weniger als 1 Minute einen vollen optimalen Runde berechnen.

Dynamische Modelle

Der Code implementiert zwei Automodelle:

• Ein 3DOF -Automodell (Längsschnitt, Lateral und Gier), das derzeit für F1 -Simulationen verwendet wird. Die verwendeten Standardparameter finden Sie in ./database/limebeer-2014-f1.xml
• Ein 6DOF-Automodell (Längsschnitt, Lateral, Branchen, Gier, Tonhöhe und Roll), das derzeit für Go-Kart-Simulationen verwendet wird. Die verwendeten Standardparameter finden Sie in ./database/roberto-lot-2016-kart.xml

Schaltungen

Schaltkreise stammen aus den von Google Earth erstellten Pfaden, beispielsweise ist die richtige Übersichtsgrenze von Catalunya in diesem Repository (Datenbank/Google_earth/catalunya_right.kml) enthalten. Schaltkreise werden dann mit einem hier enthaltenen Tool vorverarbeitet, um eine Referenzlinie, die Krümmung und den Abstand nach links/rechts (Datenbank/Catalunya_Discrete.xml) zu extrahieren.

Abhängigkeiten

Die schnellste Runde verwendet mehrere Open-Source-Bibliotheken:

• IPOPT: Interior Point Optimizer ist ein Open-Source-Softwarepaket für die nichtlineare Optimierung in großem Maßstab. Wird innerhalb dieses Projekts verwendet, um die Lösung für optimale Laptime-Probleme zu erhalten, die als NLP geschrieben wurden (nichtlineare Programmierungsproblem).
• CPPAD: C ++ Algorithmische Differenzierung. Neben Ipopt verteilt, wird es zur Berechnung analytischer Derivate verwendet.
• TinyXML2: TinyXML-2 ist ein einfacher, kleiner, effizienter C ++ XML-Parser, zum Lesen von XML-Dateien (z. B. Modellparameter, Tracks, ...)
• Logger-CPP: Ein einfacher Logger in C ++, um Druckstufen und andere interessante Add-Ons zu verarbeiten
• LION-CPP: LightWhoge-Schnittstellen für Optimierung und Numeriker, ein C ++ Paketmanager für alle oben genannten Bibliotheken sowie andere numerische Methoden wie mechanische Rahmen, Vektoralgebra und Rang-Kutta-Schemata

Installation

Windows 10

Vorkompilierte Binärdateien können für jede Veröffentlichung heruntergeladen werden.

• v0.1
• v0.2
• v0.3
• v0.4
• v0.5

Download und entpacken. Der Inhalt des Zip -Ordners ist:

• Bin: Die dynamischen Bibliotheken. Der schnellste Runden-C ++-Kern ist da. Wenn die schnellste Runde von MATLAB verwendet wird, ist Point loadlibrary() in dieses Verzeichnis.
• Hören Sie: Fastestlapc.h und schnellst_lap.py. Um Python -Skripte zu verwenden, stellen Sie sicher, dass sich dieser Ordner auf dem PYTHONPATH befindet
• Beispiele: Python Notebook -Beispiele.
• Datenbank: Auto- und Verfolgung von Daten

Mac und Linux

Dieses Projekt verwendet CMake, um den Quellcode zu erstellen und die Binärdateien zu erstellen.

Die kanonischen Schritte zum Kompilieren eines CMAKE -Projekts sind: (Angenommen, $FASTESTLAP ist die oberste Ebene des Quellcode.)

1. Erstellen Sie einen Build -Ordner.

 mkdir ${FASTESTLAP}/build

2. Führen Sie CMake aus dem Build -Ordner aus

 cd ${FASTESTLAP}/build && cmake ..

Die für CMake verfügbaren Optionen sind:

 -DCMAKE_BUILD_TYPE=Debug/Release
-DCMAKE_INSTALL_PREFIX=/path/to/install/dir
-DCODE_COVERAGE=Yes/No: enables code coverage (if so, use with -DCMAKE_BUILD_TYPE=Debug)
-DBUILD_DOC=Yes/No: builds doxygen documentation

Zu diesem Zeitpunkt wird CMAKE alle Drittanteilsabhängigkeiten herunterladen und installieren.

3. Kompilieren

 make

4. Test (optional, aber empfohlen)

 ctest --verbose

5. Installieren (optional)

 make install

Linux

Eine Docker -Build -Umgebung wird bereitgestellt und kann verwendet werden, um die gemeinsame Bibliothek zu erstellen und die Python -Bindungen zu generieren.

sh ./src/scripts/linux/docker_compile.sh

Dokumentation

Lesen Sie die neueste Online-Dokumentation am schnellsten Runden

Referenzen

[1] Tremlett, AJ und DJn Limebeer. "Optimaler Reifenverbrauch für ein Formel 1 -Auto." Fahrzeugsystemdynamik 54.10 (2016): 1448-1473.
[2] Lot, Roberto und Nicola Dal Bianco. "Rundenzeitoptimierung eines Rennsports." Fahrzeugsystemdynamik 54.2 (2016): 210-230.
[3] Dal Bianco, Nicola, Roberto Lot und Marco Gadola. "Mindestzeit optimale Kontrollsimulation eines GP2 -Rennwagens." Proceedings of the Institution of Maschinenbauingenieure, Teil D: Journal of Automobile Engineering 232.9 (2018): 1180-1195.
[4] Lot, Roberto und Matteo Massaro. "Ein symbolischer Ansatz zur Multibody -Modellierung von Straßenfahrzeugen." International Journal of Applied Mechanics 9.05 (2017): 1750068.
[5] Kelly, Daniel P. und Robin S. Sharp. "Zeitoptimale Kontrolle des Rennwagens: Eine numerische Methode, um den idealen Fahrer zu emulieren." Fahrzeugsystemdynamik 48.12 (2010): 1461-1474.
[6] Piccinini, Mattia. "Pfadplanung und Kontrolle selbstfahrender Fahrzeuge an den Grenzen des Handlings"
[7] Casanova, D. "Auf Mindestzeitfahrzeugmanövrieren: Theoretische optimale Runde"
[8] Perantoni, G. et al. "Optimale Kontrolle für ein Formel -1 -Auto mit variablen Parametern"