圖形分區框架Kahip -Karlsruhe高質量分區。
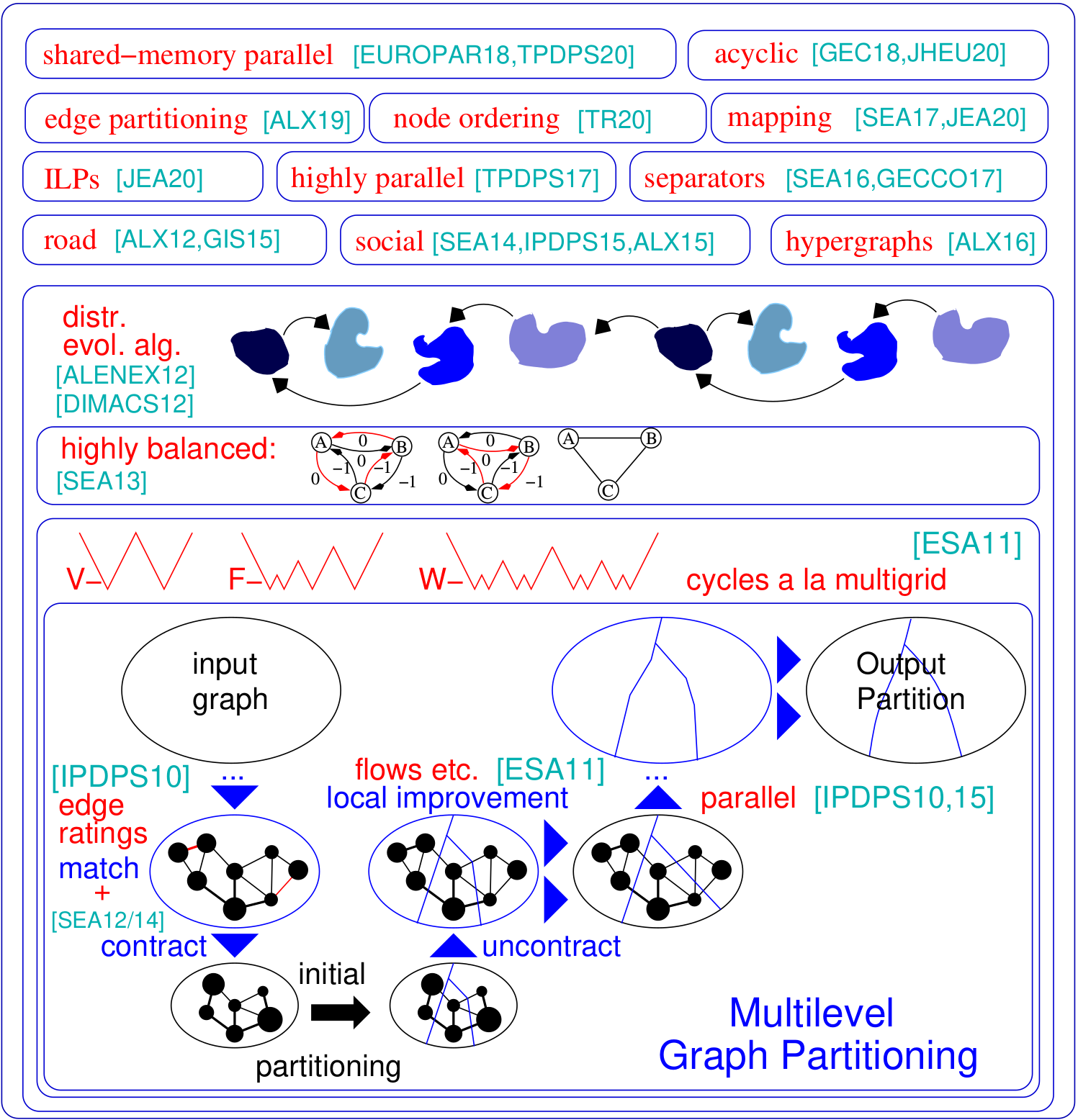
圖形分區問題要求將圖的節點設置為相等大小的塊,以便最小化塊之間運行的邊數。 Kahip是圖形分區程序的家族。 It includes KaFFPa (Karlsruhe Fast Flow Partitioner), which is a multilevel graph partitioning algorithm, in its variants Strong, Eco and Fast, KaFFPaE (KaFFPaEvolutionary), which is a parallel evolutionary algorithm that uses KaFFPa to provide combine and mutation operations, as well as KaBaPE which extends the evolutionary algorithm.此外,分區道路網絡(Buffoon)包括專門技術,以從給定分區輸出頂點分離器以及針對有效分區社交網絡的技術。這是我們框架的概述:
對Python的支持:Kahip現在也可以在Python中使用。請參閱下面的方法。
分層分區:Kahip可以計算層次分區。您所要做的就是指定層次結構,而kahip可以按照指定的方式進行多個。
節點排序算法:許多應用程序依賴於時間密集型矩陣操作(例如分解),可以通過將矩陣解釋為稀疏圖併計算出最小化所謂的填充的節點訂購來顯著加速大型稀疏矩陣。在這裡,我們添加了新的算法來計算圖中填充的減少訂單。
ILP的質量更高:ILP通常不會擴展到大型實例。我們適應它們以啟發性改進給定的分區。我們通過定義一個較小的模型來做到這一點,該模型允許我們使用對稱性破壞和其他使該方法可擴展的技術。我們包括可以用作後處理步驟,以進一步改善高質量分區。這些代碼現在包含在Kahip中。
TCMALLOC:我們添加了針對TCMalloc鏈接的可能性。根據您的系統,這可以產生總體更快的算法,因為它提供了更快的Malloc操作。
更快的IO :我們在KAFFPA(選項-MMAP_IO)中添加了一個選項,該選項會大大加快文本文件的IO - 有時是按數量級的。
對頂端的頂點和邊緣權重的添加了支持:我們擴展了Parhip的IO功能,以讀取METIS格式的加權圖。
全局多映射映射:我們添加了全局的跨度n-to Process映射算法。如果已知有關係統層次結構/體系結構的信息,則該計算並行應用程序的更好的過程映射。
Parhip中的確定性:我們添加了一個選擇以確定性運行的選項,即使用相同種子的兩次銷售將始終返回相同的結果。
版本標誌:我們添加了一個選項,以輸出您當前使用的版本,請使用程序的 - Version選項。
PARHIP(並行高質量分區):我們的分佈式內存並行分區技術旨在分區層次結構化的網絡,例如Web圖或社交網絡。
映射算法:我們的新算法將塊映射到處理器上,以根據任務圖和快速本地搜索算法的層次分區最小化整體通信時間。
邊緣分區算法:我們的新算法來計算圖形的邊緣分區。
https://kahip.github.io
您可以使用以下命令行下載Kahip:
git clone https://github.com/KaHIP/KaHIP 在開始之前,您需要安裝以下軟件包:
安裝軟件包後,只需鍵入
./compile_withcmake.sh 在這種情況下,所有二進製文件,庫和標題都位於文件夾中./deploy/
請注意,此腳本檢測到機器上可用的內核數量,並將所有這些內核用於編譯過程。如果您不想要它,請將變量ncores設置為要用於編譯的內核數。
或者使用標準CMAKE構建過程:
mkdir build
cd build
cmake ../ -DCMAKE_BUILD_TYPE=Release
make
cd ..在這種情況下,二進製文件,庫和標題在文件夾中。
我們還提供了針對TCMalloc鏈接的選項。如果安裝了它,請運行其他選項-DUSE_TCMALLOC = ON。
默認情況下,還編制了節點訂購程序。如果已安裝了METIS,則構建腳本還編譯了一個更快的節點訂購程序,該程序在調用Metis ND之前使用還原。請注意,Metis需要GKLIB(https://github.com/karypislab/gklib)。
如果您使用選項-duse_ilp = on並且已安裝了Gurobi,則構建腳本會編譯ILP程序以改進給定的分區ILP_IMPROVE和精確的求解器ILP_EXACT 。另外,您也可以將這些選項傳遞給./compile_withmake.sh:例如:
./compile_withcmake -DUSE_ILP=On我們還提供了支持64位邊緣的選項。為了使用此功能,請與選項-d64bitmode = ON一起編譯Kahip。
最後,我們提供了一種決定性決定性的選擇,例如,具有相同種子的兩次運行將為您帶來相同的結果。但是請注意,此選項可以降低分區的質量,因為初始分區算法不使用複雜的模因算法,而僅使用多級算法來計算初始分區。僅在使用Parhip作為工具時才使用此選項。如果您想對Parhip進行質量比較,請勿使用此選項。要使用此選項,請運行
./compile_withcmake -DDETERMINISTIC_PARHIP=On有關圖形格式的描述(以及所有其他程序的大量描述),請查看手冊。我們在這裡舉一個簡短的例子。
這些程序和配置繪製圖形併或多或少地對其進行了劃分。我們在這裡列出Kaffpa和Kaffpae(進化框架)及其配置。通常,配置使您可以使用模因算法將大量時間投入到解決方案質量上。模因算法也可以使用MPI並行運行。通常,您投資的時間和資源越多,分區的質量就越好。我們有很多權衡,如果您不確定哪種最適合您的應用程序,請與我們聯繫。有關算法的描述,請查看我們在手冊中列出的參考文獻。
| 用例 | 輸入 | 程式 |
|---|---|---|
| 圖格式 | graph_checker | |
| 評估分區 | 評估員 | |
| 快速分區 | 網眼 | KAFFPA預配置設置為快速 |
| 良好的分區 | 網眼 | KAFFPA預配置設置為ECO |
| 很好的分區 | 網眼 | KAFFPA預配置設置為強 |
| 最高質量 | 網眼 | kaffpae,使用Mpirun,較大的時間限制 |
| 快速分區 | 社會的 | KAFFPA預配置設置為Fsocial |
| 良好的分區 | 社會的 | KAFFPA預配置設置為社交 |
| 很好的分區 | 社會的 | KAFFPA預配置設置為社交 |
| 最高質量 | 社會的 | Kaffpae,使用Mpirun,較大的時間限制,預配置SSSOCIAL |
| 甚至更高的質量 | kaffpae,使用Mpirun,較大的時間限制,使用選項-mh_enable_tabu_search,-mh_enable_kabape |
./deploy/graph_checker ./examples/rgg_n_2_15_s0.graph ./deploy/kaffpa ./examples/rgg_n_2_15_s0.graph --k 4 --preconfiguration=strong mpirun -n 24 ./deploy/kaffpaE ./examples/rgg_n_2_15_s0.graph --k 4 --time_limit=3600 --mh_enable_tabu_search --mh_enable_kabapE 該項目的很大一部分是為具有層次群集結構(例如Web圖或社交網絡)的網絡設計的分佈式內存並行算法。不幸的是,最初針對更常規網絡的網絡開發的先前的並行圖分區器對於復雜的網絡無法很好地工作。在這裡,我們通過並行化和適應最初用於圖形聚類的標籤傳播技術來解決此問題。通過引入尺寸約束,標籤傳播適用於多級圖分區的粗化和改進階段。這樣,我們利用許多複雜網絡中存在的分層群集結構。我們通過將高度平行的進化算法應用於最高圖來獲得很高的質量。與Parmetis或Pt-Scotch這樣的最先進的系統相比,所得系統更可擴展和更高的質量。
我們的分佈式存儲器並行算法可以讀取二進製文件以及標準的METIS圖格式文件。通常,二進製文件比在並行應用程序中讀取文本文件更具擴展性。到此為止的方法是首先將METIS文件轉換為二進製文件(Ending .BGF),然後加載該文件。
| 用例 | 程式 |
|---|---|
| 並行分區 | Parhip,Graph2Binary,Graph2Binary_external,工具箱 |
| 分佈式存儲器平行於網格 | 與Preponfigs ecomesh,FastMesh,UltrafastMesh的託管 |
| 分佈式記憶平行於社交 | 與預感的生態社會,快速社會,超級社會 |
| 將梅蒂斯轉換為二進制 | graph2binary,graph2binary_external |
| 評估和轉換分區 | 工具箱 |
./deploy/graph2binary examples/rgg_n_2_15_s0.graph examples/rgg_n_2_15_s0.bgf mpirun -n 24 ./deploy/parhip ./examples/rgg_n_2_15_s0.graph --k 4 --preconfiguration=fastmesh mpirun -n 24 ./deploy/parhip ./examples/rgg_n_2_15_s0.bgf --k 4 --preconfiguration=fastmesh節點分離器問題要求將圖的節點集劃分為三組A,B和S,以使S離斷開A和B。我們使用基於流量的和局部的本地搜索算法在多級別的框架內使用基於流量的本地搜索算法來計算節點分離器。 Kahip還可以計算節點分離器。它可以使用標準節點分離器(2向)進行操作,但也可以計算K-Way節點分離器。
| 用例 | 程式 |
|---|---|
| 2向分離器 | node_separator |
| Kway分離器 | 使用kaffpa創建k部分,然後使用partition_to_vertex_separator創建一個分隔符 |
./deploy/node_separator examples/rgg_n_2_15_s0.graph可以通過將矩陣解釋為稀疏圖併計算最小化所謂的填充的節點排序來顯著加強諸如分解諸如分解之類的應用。通過在嵌套解剖之前詳盡地應用新的和現有的數據減少規則,我們可以提高質量,同時在各種實例上的運行時間進行大量改進。如果安裝了METIS,則構建腳本還編譯了FAST_NODE_ORDERING程序,該程序在運行METIS之前運行還原以計算訂購。該程序也可以通過庫獲得。
| 用例 | 程式 |
|---|---|
| 節點排序 | node_ordering(具有不同的預配置) |
| 快速節點排序 | fast_node_ordering |
./deploy/node_ordering examples/rgg_n_2_15_s0.graph ./deploy/fast_node_ordering examples/rgg_n_2_15_s0.graph以邊緣為中心的分佈式計算是一種最新技術,可以改善大型無規模網絡上的Think-A-vertex算法的缺點。為了增加此模型上的並行性,邊緣分區(將邊緣分配到大小相同的塊中)已成為傳統(基於節點)圖分區的替代方法。我們包括一種快速的平行和順序分開的圖形結構算法,該算法以可擴展的方式產生高質量的邊緣分區。我們的技術擴展到具有數十億個邊緣的網絡,並在數千個PE上有效地運行。
| 用例 | 程式 |
|---|---|
| 邊緣分區 | edge_partixing,distribute_edge_partionting |
./deploy/edge_partitioning ./examples/rgg_n_2_15_s0.graph --k 4 --preconfiguration=fast mpirun -n 4 ./deploy/distributed_edge_partitioning ./examples/rgg_n_2_15_s0.bgf --k 4 --preconfiguration=fastsocial 通信和拓撲意識過程映射是一種有力的方法,可以在具有大型分佈式內存系統上具有已知通信模式的並行應用中減少通信時間。我們將問題作為二次分配問題(QAP)解決,並包括算法以構建流程對處理器的初始映射以及快速的本地搜索算法,以進一步改善映射。通過利用通常適用於應用程序和現代超級計算機系統(例如稀疏通信模式和層次組織的通信系統)的假設,我們為這些特殊QAPS提供了更強大的算法。我們的多級構造算法採用完美平衡的圖形分區技術,並過度利用給定的通信系統層次結構。由於v3.0,我們包括了全局多元算法,這些算法將沿指定層次結構的輸入網絡直接劃分以獲取n-to-1映射,然後調用1到1映射算法以進一步改善映射。
| 用例 | 程式 |
|---|---|
| 映射到處理器網絡 | kaffpa,並使用resp使用enable_mapping選項。滲透 |
| 全球多剖面 | global_multisection with resp。滲透 |
./deploy/kaffpa examples/rgg_n_2_15_s0.graph --k 256 --preconfiguration=eco --enable_mapping --hierarchy_parameter_string=4:8:8 --distance_parameter_string=1:10:100 ./deploy/global_multisection examples/rgg_n_2_15_s0.graph --preconfiguration=eco --hierarchy_parameter_string=4:3:3:3 --distance_parameter_string=1:10:100:200我們提供ILP和ILP來改善給定分區。我們通過採用整數線性編程來擴展組合問題的附近,以進行多個本地搜索。這使我們能夠找到更複雜的組合,因此可以進一步改善解決方案。但是,開箱即用這些問題的ILP通常不會擴展到大輸入,尤其是因為圖形分配問題具有大量的對稱性 - 鑑於圖形的分區,塊IDS的每個置換率都具有相同目標和平衡的解決方案。我們定義了一個較小的圖形,稱為模型,並將模型上的圖形分區問題求解到整數線性程序的最佳性。除其他事項外,該模型使我們能夠使用對稱性破壞,這使我們可以擴展到更大的輸入。為了編譯這些程序,您需要在上面的構建過程中運行cmake。
| 用例 | 程式 |
|---|---|
| 確切的求解器 | ILP_EXACT |
| 通過ILP進行改進 | ILP_IMPROVE |
./deploy/ilp_improve ./examples/rgg_n_2_15_s0.graph --k 4 --input_partition=tmppartition4 ./deploy/ilp_exact ./examples/example_weighted.graph --k 3Kahip還提供了庫和接口,可以將算法直接鏈接到您的代碼。我們解釋了手冊中界面的細節。在下面,我們列出了鏈接Kahip庫的示例程序。此示例也可以在MISC/example_library_call/中找到。
# include < iostream >
# include < sstream >
# include " kaHIP_interface.h "
int main ( int argn, char **argv) {
std::cout << " partitioning graph from the manual " << std::endl;
int n = 5 ;
int * xadj = new int [ 6 ];
xadj[ 0 ] = 0 ; xadj[ 1 ] = 2 ; xadj[ 2 ] = 5 ; xadj[ 3 ] = 7 ; xadj[ 4 ] = 9 ; xadj[ 5 ] = 12 ;
int * adjncy = new int [ 12 ];
adjncy[ 0 ] = 1 ; adjncy[ 1 ] = 4 ; adjncy[ 2 ] = 0 ; adjncy[ 3 ] = 2 ; adjncy[ 4 ] = 4 ; adjncy[ 5 ] = 1 ;
adjncy[ 6 ] = 3 ; adjncy[ 7 ] = 2 ; adjncy[ 8 ] = 4 ; adjncy[ 9 ] = 0 ; adjncy[ 10 ] = 1 ; adjncy[ 11 ] = 3 ;
double imbalance = 0.03 ;
int * part = new int [n];
int edge_cut = 0 ;
int nparts = 2 ;
int * vwgt = NULL ;
int * adjcwgt = NULL ;
kaffpa (&n, vwgt, xadj, adjcwgt, adjncy, &nparts, &imbalance, false , 0 , ECO, & edge_cut, part);
std::cout << " edge cut " << edge_cut << std::endl;
}Kahip也可以在Python中使用。如果您想在Python首次運行中使用它
python3 -m pip install pybind11
然後運行
./compile_withcmake.sh BUILDPYTHONMODULE構建Python模型。這將構建Python模塊,還將示例callkahipfrompython.py放入部署文件夾中。您可以通過在部署文件夾中鍵入以下內容來運行此操作:
python3 callkahipfrompython.py 請注意,我們只提供初步支持,即您可能需要將一些路徑更改為compile_withcmake文件中的python。也可以在下面找到一個示例:
import kahip ;
#build adjacency array representation of the graph
xadj = [ 0 , 2 , 5 , 7 , 9 , 12 ];
adjncy = [ 1 , 4 , 0 , 2 , 4 , 1 , 3 , 2 , 4 , 0 , 1 , 3 ];
vwgt = [ 1 , 1 , 1 , 1 , 1 ]
adjcwgt = [ 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 ]
supress_output = 0
imbalance = 0.03
nblocks = 2
seed = 0
# set mode
#const int FAST = 0;
#const int ECO = 1;
#const int STRONG = 2;
#const int FASTSOCIAL = 3;
#const int ECOSOCIAL = 4;
#const int STRONGSOCIAL = 5;
mode = 0
edgecut , blocks = kahip . kaffpa ( vwgt , xadj , adjcwgt ,
adjncy , nblocks , imbalance ,
supress_output , seed , mode )
print ( edgecut )
print ( blocks )該計劃已根據MIT許可獲得許可。如果您使用我們的算法發布結果,請通過引用以下論文來確認我們的工作:
@inproceedings{sandersschulz2013,
AUTHOR = {Sanders, Peter and Schulz, Christian},
TITLE = {{Think Locally, Act Globally: Highly Balanced Graph Partitioning}},
BOOKTITLE = {Proceedings of the 12th International Symposium on Experimental Algorithms (SEA'13)},
SERIES = {LNCS},
PUBLISHER = {Springer},
YEAR = {2013},
VOLUME = {7933},
PAGES = {164--175}
}
如果您使用我們的並行分區派托,請還引用以下論文:
@inproceedings{meyerhenkesandersschulz2017,
AUTHOR = {Meyerhenke, Henning and Sanders, Peter and Schulz, Christian},
TITLE = {{Parallel Graph Partitioning for Complex Networks}},
JOURNAL = {IEEE Transactions on Parallel and Distributed Systems (TPDS)},
VOLUME = {28},
NUMBER = {9},
PAGES = {2625--2638},
YEAR = {2017}
}
如果使用映射算法,請還引用以下論文:
@inproceedings{schulztraeff2017,
AUTHOR = {Schulz, Christian and Träff, Jesper Larsson},
TITLE = {{Better Process Mapping and Sparse Quadratic Assignment}},
BOOKTITLE = {Proceedings of the 16th International Symposium on Experimental Algorithms (SEA'17)},
PUBLISHER = {Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik},
VOLUME = {75},
SERIES = {LIPIcs},
PAGES = {4:1--4:15},
YEAR = {2017}
}
如果您使用邊緣分區算法,請還引用以下論文:
@inproceedings{edgepartitioning2019,
AUTHOR = {Schlag, Sebastian and Schulz, Christian and Seemaier, Daniel and Strash, Darren},
TITLE = {{Scalable Edge Partitioning}},
BOOKTITLE = {Proceedings of the 21th Workshop on Algorithm Engineering and Experimentation (ALENEX)},
PUBLISHER = {SIAM},
PAGES = {211--225},
YEAR = {2019}
}
如果使用節點訂購算法,請還引用以下論文:
@article{DBLP:journals/corr/abs-2004-11315,
author = {Wolfgang Ost and
Christian Schulz and
Darren Strash},
title = {Engineering Data Reduction for Nested Dissection},
journal = {CoRR},
volume = {abs/2004.11315},
year = {2020},
url = {https://arxiv.org/abs/2004.11315},
archivePrefix = {arXiv},
eprint = {2004.11315},
timestamp = {Tue, 28 Apr 2020 16:10:02 +0200},
biburl = {https://dblp.org/rec/journals/corr/abs-2004-11315.bib},
bibsource = {dblp computer science bibliography, https://dblp.org}
}
如果您使用ILP算法來改進分區,請同時引用以下論文:
@inproceedings{DBLP:conf/wea/HenzingerN018,
author = {Alexandra Henzinger and
Alexander Noe and
Christian Schulz},
title = {ILP-based Local Search for Graph Partitioning},
booktitle = {17th International Symposium on Experimental Algorithms, {SEA} 2018},
pages = {4:1--4:15},
year = {2018},
url = {https://doi.org/10.4230/LIPIcs.SEA.2018.4},
doi = {10.4230/LIPIcs.SEA.2018.4},
series = {LIPIcs},
volume = {103},
publisher = {Schloss Dagstuhl - Leibniz-Zentrum f{"{u}}r Informatik}
}
Yaroslav Akhremtsev
阿迪爾·恰布拉(Adil Chhabra)
Marcelo Fonseca Faraj
羅蘭·格蘭茲(Roland Glantz)
亞歷山德拉·亨辛格(Alexandra Henzinger)
丹尼斯·盧克森(Dennis Luxen)
Henning Meyerhenke
亞歷山大·諾
馬克·奧爾森
拉拉·奧斯特(Lara Ost)
Ilya Safro
彼得·桑德斯
海克·薩爾格森(Hayk Sargsyan)
塞巴斯蒂安·施拉格(Sebastian Schlag)
克里斯蒂安·舒爾茨(維護者)
丹尼爾·梅西耶(Daniel Seemaier)
達倫·斯特拉什(Darren Strash)
JesperLarssonTräff