Download de KaHIP - Download do código -fonte KaHIP

KaHIP

C/C++

v3.17

Baixar

Kahip v3.17

A estrutura de particionamento de gráficos Kahip - Karlsruhe Particionamento de alta qualidade.

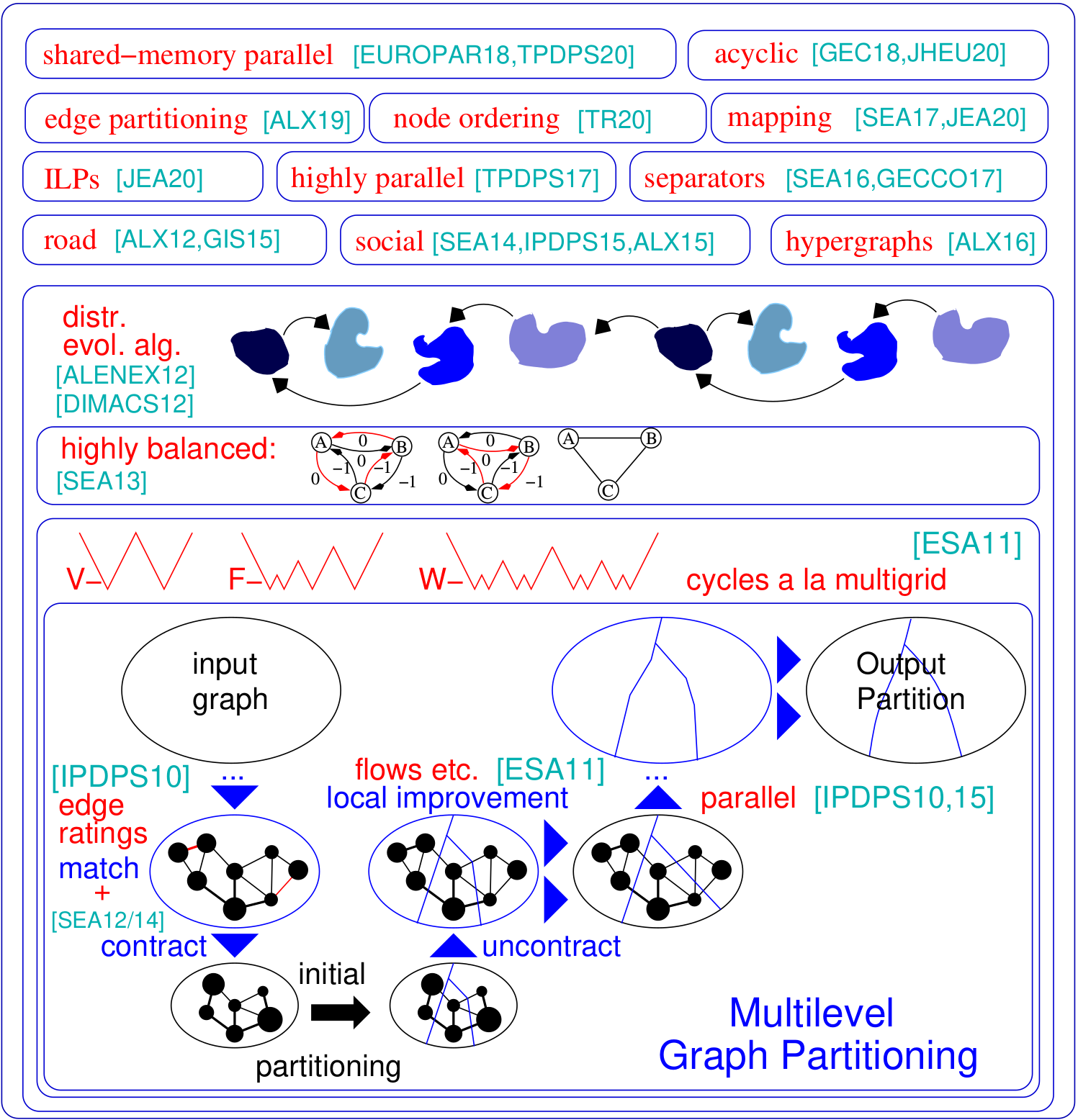
O problema de particionamento de gráficos solicita uma divisão do nó de um gráfico definido em blocos de tamanho igual, de modo que o número de arestas que executam entre os blocos é minimizado. Kahip é uma família de programas de particionamento de gráficos. Inclui Kaffpa (partitiote em fluxo rápido de Karlsruhe), que é um algoritmo de particionamento de gráficos multiníveis, em suas variantes fortes, ecológicas e rápidas, kaffpae (kaffpaevolutionary), que é um algoritmo evolutivo paralelo que usa o KaffPa para combinar e as operações de mutização, como o algoritmo que usa o KaffPA para combinar e mutuários, como o algoritmo e o algoritmo que usa o Kaffpa para combinar e as operações de mutuários, assim como o algoritmo que usa o KaffPA para combinar e mutimização, o que é um algoritmo evolutivo, o que usa o Kaffpa para combinar e as operações de mutização, como o algoritmo que usa o KaffPA para combinar e mutimização, assim como as operações de algorma que usa o KaffPA para combinar e não Além disso, técnicas especializadas são incluídas nas redes rodoviárias de partição (bufão), para produzir um separador de vértices de uma determinada partição, bem como técnicas voltadas para o particionamento eficiente das redes sociais. Aqui está uma visão geral de nossa estrutura:

Visão geral da estrutura

Novo em v3.14:

Suporte para Python : Kahip agora também pode ser usado no Python. Veja abaixo como fazer isso.

Partições hierárquicas : KAHIP pode calcular partições hierárquicas. Tudo o que você precisa fazer é especificar a hierarquia e o Kahip está pronto para ir e faz a multissecção conforme especificado.

Algoritmos de ordenação de nós : Muitas aplicações dependem de operações de matriz intensiva em tempo intensiva, como a fatoração, que podem ser aceleradas significativamente para grandes matrizes esparsas, interpretando a matriz como um gráfico esparso e calculando uma ordem de um nó que minimiza a chamada preenchimento. Aqui, adicionamos novos algoritmos para calcular pedidos reduzidos de preenchimento em gráficos.

ILPs para qualidade ainda mais alta : os ILPs normalmente não são escalados para grandes instâncias. Nós os adaptamos a melhorar heuristicamente uma determinada partição. Fazemos isso definindo um modelo muito menor que nos permite usar a quebra de simetria e outras técnicas que tornam a abordagem escalável. Incluímos ILPs que podem ser usados como uma etapa de pós-processamento para melhorar ainda mais as partições de alta qualidade. Os códigos estão agora incluídos em Kahip.

TCMALLOC: Adicionamos a possibilidade de vincular o TCMalloc. Dependendo do seu sistema, isso pode produzir um algoritmo geral mais rápido, pois fornece operações mais rápidas do MALLOC.

IO mais rápido : adicionamos uma opção ao kaffpa (opção -mmap_io) que acelera significativamente o IO dos arquivos de texto -às vezes por uma ordem de magnitude.

Suporte adicionado para pesos de vértice e borda em Parhip : estendemos a funcionalidade de IO do parhip para ler gráficos ponderados no formato Metis.

Mapeamento global de multissecção : adicionamos algoritmos globais de mapeamento de processos n-1 multisseccionários. Isso calcula melhor o mapeamento de processos para aplicações paralelas se forem conhecidas informações sobre a hierarquia/arquitetura do sistema.

Determinismo em Parhip : Adicionamos uma opção para executar o parhips deterministicamente, ou seja, duas corridas de parhip usando a mesma semente sempre retornarão o mesmo resultado.

Sinalizador de versão : adicionamos uma opção para produzir a versão que você está usando atualmente, use a opção --version dos programas.

Novo em v2.10:

Parhip (partição paralela de alta qualidade): Nossas técnicas de particionamento paralelo de memória distribuídas são projetadas para particionar redes hierarquicamente estruturadas, como gráficos da Web ou redes sociais.

Algoritmos de mapeamento: nossos novos algoritmos para mapear os blocos nos processadores para minimizar o tempo geral de comunicação com base nas partições hierárquicas do gráfico de tarefas e nos algoritmos de pesquisa local rápido.

Algoritmos de particionamento de borda: nossos novos algoritmos para calcular as partições de borda de gráficos.

Site do projeto principal:

https://kahip.github.io

Notas de instalação

Download Kahip:

Você pode baixar o Kahip com a seguinte linha de comando:

 git clone https://github.com/KaHIP/KaHIP

Compilando kahip:

Antes de começar, você precisa instalar os seguintes pacotes de software:

Se você deseja usar algoritmos paralelos contidos na estrutura (por exemplo, parhip), você precisa do OpenMPI (https://www.open-mpi.org/). Se você não quiser executar o Parhip, pode facilmente se livrar dessa dependência.

Depois de instalar os pacotes, basta digitar

 ./compile_withcmake.sh

Nesse caso, todos os binários, bibliotecas e cabeçalhos estão na pasta ./deploy/

Observe que este script detecta a quantidade de núcleos disponíveis em sua máquina e usa todos eles para o processo de compilação. Se você não quiser, defina os ncores variáveis para o número de núcleos que você gostaria de usar para compilação.

Alternativamente, use o processo de construção cmake padrão:

 mkdir build
cd build 
cmake ../ -DCMAKE_BUILD_TYPE=Release     
make 
cd ..

Nesse caso, os binários, bibliotecas e cabeçalhos estão na pasta ./build, bem como ./build/parallel/parallel_src/

Também fornecemos a opção de vincular o TCMalloc. Se você o tiver instalado, execute o cmake com a opção adicional -duse_tcmalloc = on.

Por padrão, os programas de pedidos de nó também são compilados. Se você instalou o Metis, o script de compilação também compila um programa de pedidos de nós mais rápido que usa reduções antes de chamar Metis ND. Observe que Metis requer Gklib (https://github.com/karypislab/gklib).

Se você usar a opção -duse_ilp = ativado e tiver instalado o Gurobi, o script de compilação compila os programas ILP para melhorar uma determinada partição ilp_improve e um solucionador exato ILP_EXACT . Como alternativa, você também pode passar essas opções para ./compile_withmake.sh, por exemplo:

 ./compile_withcmake -DUSE_ILP=On

Também fornecemos uma opção para suportar arestas de 64 bits. Para usar isso, compile Kahip com a opção -d64bitmode = on.

Por fim, fornecemos uma opção para o determinismo no Parhip, por exemplo, duas corridas com a mesma semente fornecerão o mesmo resultado. Observe, no entanto, que essa opção pode reduzir a qualidade das partições, pois os algoritmos iniciais de particionamento não usam algoritmos meméticos sofisticados, mas apenas algoritmos multiníveis para calcular as partições iniciais. Use apenas esta opção se você usar o Parhip como uma ferramenta. Não use esta opção se desejar fazer comparações de qualidade com o Parhip. Para fazer uso desta opção, execute

 ./compile_withcmake -DDETERMINISTIC_PARHIP=On

Programas de execução

Para uma descrição do formato do gráfico (e uma descrição extensa de todos os outros programas), dê uma olhada no manual. Damos exemplos curtos aqui.

Visão geral dos programas e USECASE

Problema de particionamento padrão

Esses programas e configurações pegam um gráfico e a particionam mais ou menos sequencialmente. Listamos aqui Kaffpa e Kaffpae (a estrutura evolutiva) e suas configurações. Em geral, as configurações são tais que você pode investir muito tempo na qualidade da solução usando o algoritmo memético. O algoritmo memético também pode ser executado em paralelo usando MPI. Em geral, quanto mais tempo e recursos você investe, melhor será a qualidade da sua partição. Temos muitas compensações, entre em contato conosco se não tiver certeza do que funciona melhor para o seu aplicativo. Para uma descrição do algoritmo, dê uma olhada nas referências que listamos no manual.

Caso de uso	Entrada	Programas
Formato do gráfico		Graph_Checker
Avaliar partições		Avaliador
Partição rápida	Malhas	Preconfiguração do Kaffpa definido como rápido
Boa partição	Malhas	Kaffpa Preconfiguration definido como Eco
Muito bom particionamento	Malhas	Preconfiguração da Kaffpa definida como forte
Mais alta qualidade	Malhas	kaffpae, use mpirun, grande limite de tempo
Partição rápida	Social	Preconfiguração de Kaffpa definida como fsocial
Boa partição	Social	Kaffpa Preconfiguration definido como ESocial
Muito bom particionamento	Social	Preconfiguração de Kaffpa definida como SSocial
Mais alta qualidade	Social	kaffpae, use mpirun, grande limite de tempo, pré -configuração ssocial
Qualidade ainda maior		kaffpae, use mpirun, grande limite de tempo, use as opções -mh_enable_tabu_search, - -mh_enable_kabape

Exemplo é executado

 ./deploy/graph_checker ./examples/rgg_n_2_15_s0.graph

 ./deploy/kaffpa ./examples/rgg_n_2_15_s0.graph --k 4  --preconfiguration=strong

 mpirun -n 24 ./deploy/kaffpaE ./examples/rgg_n_2_15_s0.graph --k 4  --time_limit=3600 --mh_enable_tabu_search --mh_enable_kabapE

Paralelo de memória distribuída

Uma grande parte do projeto é distribuída algoritmos paralelos de memória projetados para redes com uma estrutura hierárquica de cluster, como gráficos da Web ou redes sociais. Infelizmente, as partições de gráficos paralelas anteriores se desenvolveram originalmente para redes mais regulares do tipo malha não funcionam bem para redes complexas. Aqui, abordamos esse problema paralelo e adaptando a técnica de propagação do rótulo originalmente desenvolvida para o cluster de gráficos. Ao introduzir restrições de tamanho, a propagação do rótulo se torna aplicável tanto para a fase de ator de refinamento quanto para a partição de gráficos multiníveis. Dessa forma, exploramos a estrutura hierárquica do cluster presente em muitas redes complexas. Obtemos qualidade muito alta aplicando um algoritmo evolutivo altamente paralelo ao gráfico mais grosseiro. O sistema resultante é mais escalável e alcança uma qualidade mais alta do que os sistemas de última geração, como Parmetis ou Pt-Cotch.

Nosso algoritmo paralelo de memória distribuído pode ler arquivos binários, bem como arquivos de formato de gráfico de metis padrão. Os arquivos binários são, em geral, muito mais escaláveis do que a leitura de arquivos de texto em aplicativos paralelos. A maneira de ir aqui é converter o arquivo Metis em um arquivo binário primeiro (encerrar .bgf) e depois carregar este.

Caso de uso	Programas
Particionamento paralelo	Parhip, Graph2Binary, Graph2Binary_External, caixa de ferramentas
Memória distribuída paralela, malha	Parhip with PrecOnfigs Ecomesh, FastMesh, UltraAfastMesh
Memória distribuída paralela, social	Parhip with PrecOnfigs EcoSocial, FastSocial, UltrafastSocial
Converter metis em binário	Graph2Binary, Graph2Binary_External
Avaliar e converter partições	caixa de ferramentas

Exemplo é executado

 ./deploy/graph2binary examples/rgg_n_2_15_s0.graph examples/rgg_n_2_15_s0.bgf

 mpirun -n 24 ./deploy/parhip ./examples/rgg_n_2_15_s0.graph --k 4 --preconfiguration=fastmesh

 mpirun -n 24 ./deploy/parhip ./examples/rgg_n_2_15_s0.bgf --k 4 --preconfiguration=fastmesh

Separadores de nós

O problema do separador do nó solicita a partição do conjunto de nó de um gráfico em três conjuntos A, B e S, de modo que a remoção de S desconecte A e B. Usamos algoritmos de pesquisa local baseados em fluxo e localizados em uma estrutura multinível para calcular os separadores de nó. Kahip também pode calcular separadores de nós. Pode fazer isso com um separador de nó padrão (2 vias), mas também pode calcular os separadores de nós K-Way.

Caso de uso	Programas
Separadores de 2 vias	node_separator
Kway Separators	Use Kaffpa para criar K-Partition e depois partição_to_vertex_separator para criar um separador

Exemplo é executado

 ./deploy/node_separator examples/rgg_n_2_15_s0.graph

Pedido de nó

Aplicações como a fatoração podem ser aceleradas significativamente para grandes matrizes esparsas, interpretando a matriz como um gráfico esparso e calculando uma ordem de nó que minimiza o chamado preenchimento. Ao aplicar as regras de redução de dados novas e existentes exaustivamente antes da dissecção aninhada, obtemos uma qualidade aprimorada e ao mesmo tempo grandes melhorias no tempo de execução em várias instâncias. Se o Metis estiver instalado, o script de compilação também compila o programa fast_node_ordering, que executa reduções antes de executar o Metis para calcular um pedido. Os programas também estão disponíveis na biblioteca.

Caso de uso	Programas
Pedido de nó	Node_ordering (com diferentes pré -configurações)
Pedido de nó rápido	fast_node_ordering

Exemplo é executado

 ./deploy/node_ordering examples/rgg_n_2_15_s0.graph

 ./deploy/fast_node_ordering examples/rgg_n_2_15_s0.graph

Partição de borda

Os cálculos distribuídos centrados em arestas apareceram como uma técnica recente para melhorar as deficiências de algoritmos de pensamento como um vertex em redes livres de larga escala. Para aumentar o paralelismo nesse modelo, o particionamento de borda-particionando bordas em blocos de tamanho aproximado-emergiu como uma alternativa ao particionamento de gráficos tradicional (baseado em nó). Incluímos um algoritmo de construção de gráficos paralelo e sequencial e sequencial que produz partições de borda de alta qualidade de maneira escalável. Nossa técnica escala para redes com bilhões de arestas e é executada com eficiência em milhares de PES.

Caso de uso	Programas
Partição de borda	Edge_Partitioning, distribued_edge_Partitioning

Exemplo é executado

 ./deploy/edge_partitioning ./examples/rgg_n_2_15_s0.graph --k 4 --preconfiguration=fast

 mpirun -n 4 ./deploy/distributed_edge_partitioning ./examples/rgg_n_2_15_s0.bgf --k 4 --preconfiguration=fastsocial

Mapeamento de processos

O mapeamento de processos conscientes da comunicação e da topologia é uma abordagem poderosa para reduzir o tempo de comunicação em aplicações paralelas com padrões de comunicação conhecidos em sistemas de memória grandes e distribuídos. Abordamos o problema como um problema de atribuição quadrática (QAP) e incluímos algoritmos para construir mapeamentos iniciais de processos para processadores, bem como algoritmos de pesquisa locais rápidos para melhorar ainda mais os mapeamentos. Ao explorar suposições que normalmente se mantêm para aplicativos e sistemas modernos de supercomputadores, como padrões de comunicação escassa e sistemas de comunicação organizados hierarquicamente, chegamos a algoritmos significativamente mais poderosos para esses QAPs especiais. Nossos algoritmos de construção multinível empregam técnicas de particionamento de gráficos perfeitamente equilibradas e exploram excessivamente a hierarquia do sistema de comunicação fornecido. Desde a v3.0, incluímos algoritmos globais de multissecção que particionam diretamente a rede de entrada ao longo da hierarquia especificada para obter um mapeamento n-1 e depois ligue para os algoritmos de mapeamento de 1 a 1 para melhorar ainda mais o mapeamento.

Caso de uso	Programas
Mapeamento para redes de processador	Kaffpa e Use a opção Enable_Mapping com resp. Perconfigurações
Multissecção global	Global_multisection com resp. Perconfigurações

Exemplo é executado

 ./deploy/kaffpa examples/rgg_n_2_15_s0.graph --k 256 --preconfiguration=eco --enable_mapping --hierarchy_parameter_string=4:8:8 --distance_parameter_string=1:10:100

 ./deploy/global_multisection examples/rgg_n_2_15_s0.graph --preconfiguration=eco  --hierarchy_parameter_string=4:3:3:3 --distance_parameter_string=1:10:100:200

ILP (Solver exato) e melhorias de ILP

Fornecemos um ILP e um ILP para melhorar uma determinada partição. Estendemos a vizinhança do problema de combinação para várias pesquisas locais, empregando programação linear inteira. Isso nos permite encontrar combinações ainda mais complexas e, portanto, melhorar ainda mais as soluções. No entanto, fora da caixa, os ILPs para o problema normalmente não escalam para grandes entradas, em particular porque o problema de particionamento de gráficos tem uma quantidade muito grande de simetria - dada a partição do gráfico, cada permutação dos IDs de bloco fornece uma solução com o mesmo objetivo e equilíbrio. Definimos um gráfico muito menor, chamado modelo, e resolvemos o problema de particionamento de gráficos no modelo de otimização pelo programa linear inteiro. Além de outras coisas, esse modelo nos permite usar a quebra de simetria, o que nos permite escalar para entradas muito maiores. Para compilar esses programas, você precisa executar o CMake no processo de construção acima como cmake ../ -dcmake_build_type = release -duse_ilp = on ou run ./compile_withcmake -duse_ilp = on.

Caso de uso	Programas
Solucionador exato	ilp_exact
Melhoria via ILP	ilp_improve

Exemplo é executado

 ./deploy/ilp_improve ./examples/rgg_n_2_15_s0.graph --k 4 --input_partition=tmppartition4

 ./deploy/ilp_exact ./examples/example_weighted.graph  --k 3

Vinculando a biblioteca Kahip

O Kahip também oferece bibliotecas e interfaces para vincular os algoritmos diretamente ao seu código. Explicamos os detalhes da interface no manual. Abaixo, listamos um programa de exemplo que vincula a biblioteca Kahip. Este exemplo também pode ser encontrado em misc/exemplo_library_call/.

# include < iostream >
# include < sstream >

# include " kaHIP_interface.h "


int main ( int argn, char **argv) {

        std::cout <<  " partitioning graph from the manual "  << std::endl;

        int n            = 5 ;
        int * xadj        = new int [ 6 ];
        xadj[ 0 ] = 0 ; xadj[ 1 ] = 2 ; xadj[ 2 ] = 5 ; xadj[ 3 ] = 7 ; xadj[ 4 ] = 9 ; xadj[ 5 ] = 12 ;

        int * adjncy      = new int [ 12 ];
        adjncy[ 0 ]  = 1 ; adjncy[ 1 ]  = 4 ; adjncy[ 2 ]  = 0 ; adjncy[ 3 ]  = 2 ; adjncy[ 4 ]  = 4 ; adjncy[ 5 ]  = 1 ; 
        adjncy[ 6 ]  = 3 ; adjncy[ 7 ]  = 2 ; adjncy[ 8 ]  = 4 ; adjncy[ 9 ]  = 0 ; adjncy[ 10 ] = 1 ; adjncy[ 11 ] = 3 ; 
        
        double imbalance = 0.03 ;
        int * part        = new int [n];
        int edge_cut     = 0 ;
        int nparts       = 2 ;
        int * vwgt        = NULL ;
        int * adjcwgt     = NULL ;

        kaffpa (&n, vwgt, xadj, adjcwgt, adjncy, &nparts, &imbalance, false , 0 , ECO, & edge_cut, part);

        std::cout <<  " edge cut " <<  edge_cut  << std::endl;
}

Usando Kahip em Python

Kahip também pode ser usado em Python. Se você quiser usá -lo em Python, primeiro execução

 python3 -m pip install pybind11

Em seguida, corra

 ./compile_withcmake.sh BUILDPYTHONMODULE

Para construir o modelo Python. Isso criará o módulo Python e também dará um exemplo de callkahipfrompython.py na pasta de implantação. Você pode executar isso digitando o seguinte na pasta de implantação:

 python3 callkahipfrompython.py

Observe que fornecemos apenas suporte preliminar, ou seja, você pode precisar alterar alguns caminhos para o Python dentro do arquivo compile_withcmake. Um exemplo também pode ser encontrado abaixo:

 import kahip ;

#build adjacency array representation of the graph
xadj           = [ 0 , 2 , 5 , 7 , 9 , 12 ];
adjncy         = [ 1 , 4 , 0 , 2 , 4 , 1 , 3 , 2 , 4 , 0 , 1 , 3 ];
vwgt           = [ 1 , 1 , 1 , 1 , 1 ]
adjcwgt        = [ 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 ]
supress_output = 0
imbalance      = 0.03
nblocks        = 2 
seed           = 0

# set mode 
#const int FAST           = 0;
#const int ECO            = 1;
#const int STRONG         = 2;
#const int FASTSOCIAL     = 3;
#const int ECOSOCIAL      = 4;
#const int STRONGSOCIAL   = 5;
mode = 0 

edgecut , blocks = kahip . kaffpa ( vwgt , xadj , adjcwgt , 
                              adjncy ,  nblocks , imbalance , 
                              supress_output , seed , mode )

print ( edgecut )
print ( blocks )

Licença

O programa está licenciado sob licença do MIT. Se você publicar resultados usando nossos algoritmos, reconheça nosso trabalho citando o seguinte artigo:

 @inproceedings{sandersschulz2013,
             AUTHOR = {Sanders, Peter and Schulz, Christian},
             TITLE = {{Think Locally, Act Globally: Highly Balanced Graph Partitioning}},
             BOOKTITLE = {Proceedings of the 12th International Symposium on Experimental Algorithms (SEA'13)},
             SERIES = {LNCS},
             PUBLISHER = {Springer},
             YEAR = {2013},
             VOLUME = {7933},
             PAGES = {164--175}
}

Se você usar nosso paralelo paralelo, cite também o seguinte artigo:

 @inproceedings{meyerhenkesandersschulz2017,
             AUTHOR = {Meyerhenke, Henning and Sanders, Peter and Schulz, Christian},
             TITLE = {{Parallel Graph Partitioning for Complex Networks}},
             JOURNAL = {IEEE Transactions on Parallel and Distributed Systems (TPDS)},
             VOLUME = {28},
             NUMBER = {9},
             PAGES = {2625--2638},
             YEAR = {2017}
}

Se você usar o algoritmo de mapeamento, cite o seguinte artigo:

 @inproceedings{schulztraeff2017,
             AUTHOR = {Schulz, Christian and Träff, Jesper Larsson},
             TITLE = {{Better Process Mapping and Sparse Quadratic Assignment}},
             BOOKTITLE = {Proceedings of the 16th International Symposium on Experimental Algorithms (SEA'17)},
             PUBLISHER = {Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik},
             VOLUME = {75},
             SERIES = {LIPIcs},
             PAGES = {4:1--4:15},
             YEAR = {2017}
}

Se você usar algoritmos de particionamento de borda, cite o seguinte artigo:

 @inproceedings{edgepartitioning2019,
             AUTHOR = {Schlag, Sebastian and Schulz, Christian and Seemaier, Daniel and Strash, Darren},
             TITLE = {{Scalable Edge Partitioning}},
             BOOKTITLE = {Proceedings of the 21th Workshop on Algorithm Engineering and Experimentation (ALENEX)},
             PUBLISHER = {SIAM},
             PAGES = {211--225},
             YEAR = {2019}
}

Se você usar algoritmos de pedidos de nó, cite também o seguinte artigo:

 @article{DBLP:journals/corr/abs-2004-11315,
  author    = {Wolfgang Ost and
               Christian Schulz and
               Darren Strash},
  title     = {Engineering Data Reduction for Nested Dissection},
  journal   = {CoRR},
  volume    = {abs/2004.11315},
  year      = {2020},
  url       = {https://arxiv.org/abs/2004.11315},
  archivePrefix = {arXiv},
  eprint    = {2004.11315},
  timestamp = {Tue, 28 Apr 2020 16:10:02 +0200},
  biburl    = {https://dblp.org/rec/journals/corr/abs-2004-11315.bib},
  bibsource = {dblp computer science bibliography, https://dblp.org}
}

Se você usar algoritmos ILP para melhorar uma partição, cite também o seguinte artigo:

 @inproceedings{DBLP:conf/wea/HenzingerN018,
  author    = {Alexandra Henzinger and
               Alexander Noe and
               Christian Schulz},
  title     = {ILP-based Local Search for Graph Partitioning},
  booktitle = {17th International Symposium on Experimental Algorithms, {SEA} 2018},
  pages     = {4:1--4:15},
  year      = {2018},
  url       = {https://doi.org/10.4230/LIPIcs.SEA.2018.4},
  doi       = {10.4230/LIPIcs.SEA.2018.4},
  series    = {LIPIcs},
  volume    = {103},
  publisher = {Schloss Dagstuhl - Leibniz-Zentrum f{"{u}}r Informatik}
}